严寒地区某碾压混凝土坝稳定温度场仿真计算
2016-11-08张俊霞张浩
张俊霞,张浩
(1.海河水利委员会水利信息网络中心,天津300170;2.河北省水利水电勘测设计研究院,天津300250)
严寒地区某碾压混凝土坝稳定温度场仿真计算
张俊霞1,张浩2
(1.海河水利委员会水利信息网络中心,天津300170;2.河北省水利水电勘测设计研究院,天津300250)
某碾压混凝土坝地处北方寒冷地区,冬季温度低,夏季温度高,气温年内变幅大,日气温变幅大,寒潮频繁且降温大,对大坝的温控防裂极为不利。为了研究混凝土坝温度应力的分布规律,进而提出满足温控防裂的温控标准和相应的防裂措施,选择主河床最高典型挡水坝段、典型溢流坝段、典型发电引水坝段以及典型底孔坝段混凝土作为重点研究对象,根据热传导理论和有限元方法,采用水温统计的成果进行温度场仿真计算,结果表明大坝的稳定温度为7~9℃。
寒冷地区;碾压混凝土坝;温度场;仿真;有限元
大体积混凝土坝在初始影响消失后,坝体温度完全取决于随时间变化的上、下游水温和气温,但它们具有实际意义的影响深度不超过7~10m[1,2],坝体内部温度基本上是稳定的。稳定温度场是计算温度应力和确定基础温差的基准,是制定施工期温度控制标准的重要依据,也是确定灌浆温度的重要参考资料。因此,稳定温度场的分析与计算是温度控制设计中必不可少的内容。
1 工程概况
地处寒冷地区的某水库枢纽建筑物主要包括拦河坝和电站。拦河坝为碾压混凝土重力坝,为2级建筑物,坝顶全长533m,坝顶宽7.0~18.0m,最大坝高50.1m。电站为坝后式,装机容量1 580 kW,最大引水流量10.86m3/s;电站坝段同时布置1条生态放水洞,放水洞与电站进水口共用1个竖井式分层取水口,下游接直径0.8m的引水管将库水引入下游河道。
拦河坝共分24个坝段,横缝间距17.5~24m,从右至左依次为:1~4#为右岸非溢流坝段,坝顶长84m;5~9#为溢流坝段,坝顶长101m;10#为河床非溢流坝段,坝顶长24m;11~12#为底孔坝段,坝顶长40m;13#为电站坝段,坝顶长20m;14~24#为左岸非溢流坝段,坝顶总长264m。底孔和电站坝段底宽均为45.325m,非溢流坝段和溢流坝段最大底宽为39.325m,不设纵缝;底孔和电站坝段上部常态混凝土最大浇筑块长度为28.5m,亦不设纵缝。
本工程主体工程混凝土总量约55万m3,其中坝体二级配碾压混凝土约9万m3、三级配碾压混凝土30万m3,坝体变态混凝土3万m3、常态混凝土13万m3,电站常态混凝土0.9万m3。
2 大坝稳定温度场计算原理
2.1热传导微分方程
直角坐标系下,均匀的各向同性的具有内部热源的固体的热传导微分方程式为:
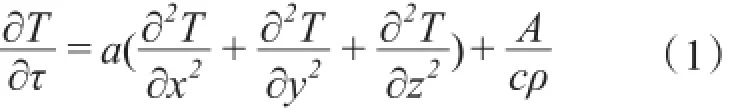
式中:T为温度(℃);a=λ/cρ为导温系数,又称温度扩散系数(m2/h);τ为时间(h);A为内部热源的单位功率[kJ/(m3·h)];λ为导热系数[kJ/(m·h·℃)];c为比热[kJ/(kg·℃)];ρ为密度(kg/m3)。
绝热条件下,混凝土的温度上升速度为:

式中:θ为混凝土的绝热条件下温度上升值(℃);W为单位水泥用量(kg/m3);q为单位质量水泥在单位时间内释放的水化热[kJ/(kg·h)]。
根据式(2),热传导微分方程式(1)可改写为:
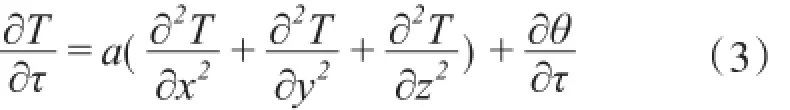
对于无水化热或不考虑水化热的问题,∂θ/∂τ=0。如果温度场不随时间变化则称为稳定温度场,因而∂T/∂τ=0,其热传导微分方程则为:
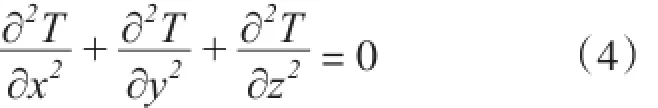
2.2有限单元法
由2.1可知,在坝体内部即在区域R内,稳定温度场T(x,y,z)应满足式(4)。
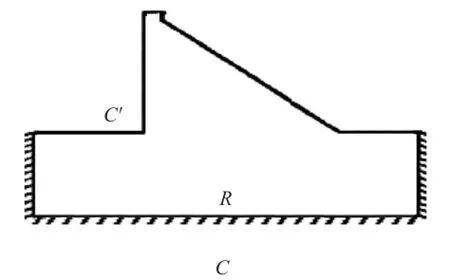
图1 坝体示意
在边界C(如图1所示)上,满足绝热条件,即:

式中:n为边界C的法线。
在边界C'上,满足第一类边界条件,即:

式中:Tb为给定的边界温度(℃),在上游面Tb取值为年平均水温,在下游面Tb取值为年平均气温与太阳辐射影响之和。
将描述稳定温度场的微分方程转化为积分方程,这就是所谓解法的变分原理。因此,上述热传导问题就等价于下列泛函的极值问题:
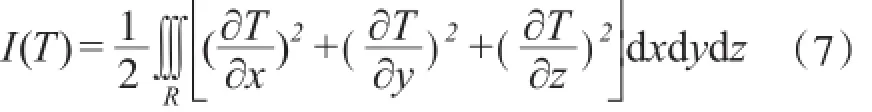
式中:I(T)为温度T的泛函;R为积分域,即坝体内部区域,如图1所示。
数学推导已经证明,式(4)和(5)恰是泛函式(7)的尤拉方程,而满足尤拉方程的温度场T(x,y,z)必然使泛函式(7)取得极小值。这样,便可将求解微分方程式(4)、(5)的问题转换为求泛函I(T)的极小值问题;而求泛函I(T)的极小值问题便可采用有限单元法解决。
由于泛函式(7)的尤拉方程只包括式(4)和(5),并未包含式(6)。按照微分方程求解稳定温度场的经典方法,是在边界条件式(5)和(6)的约束下寻找满足式(4)的解的,现在应用变分原理,通过求式(7)的极值来求解稳定温度场,却丢失了边界条件式(6)。因此,应用变分原理求解上述稳定温度场时,必须是在边界条件式(6)的约束下,求泛函I(T)的极小值。由于式(7)的尤拉方程并不包含式(6),故此时称式(6)为强加边界条件。
至此,问题归结为,在边界条件式(6)的约束下,用有限元法求解泛函式(7)的极小值[2]。
由此得到下列方程组:

3 三维有限元模型和计算资料
3.1三维有限元模型
选取典型的挡水坝段、溢流坝段、厂房坝段和底孔坝段,进行大坝稳定温度场的仿真计算,典型坝段的剖面如图2—5所示。
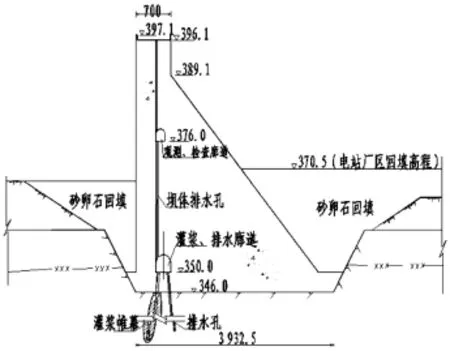
图2 大坝典型挡水坝段剖面
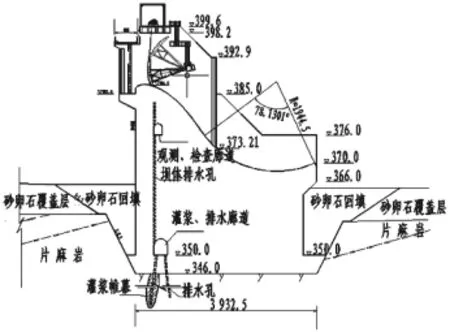
图3 大坝典型溢流坝段剖面
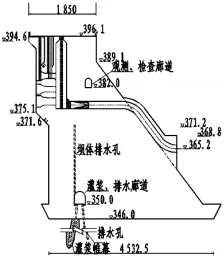
图4 大坝电站坝段剖面
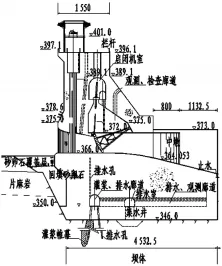
图5 大坝电站底孔坝段剖面
典型挡水坝段取14#坝段,有限元模型取半个厚度的坝段。坝段对称剖面坝踵处为坐标原点;X为水流方向,由上游指向下游为正向;Y为垂直水流方向,正向由右岸指向左岸;Z为竖直方向,竖直向上为正。坝基取竖直向下及上、下游方向各1.5倍坝高的岩体。挡水坝段三维有限元计算模型如图6所示,用8节点等参空间单元,其中共计6 016个单元、8 045个节点。溢流坝段三维有限元计算模型如图7所示,用8节点等参空间单元,其中共计5 268个单元、6 664个节点。厂房坝段三维有限元计算模型如图8所示,用8节点等参空间单元,其中共计6 816个单元、8 430个节点。底孔坝段三维有限元计算模型如图9所示,用8节点等参空间单元,其中共计3 552个单元、4 543个节点。
3.2计算资料
大坝地处北方寒冷地区,2001—2010年的气象资料如下:该地区多年平均气温为8.5℃,冬季月平均气温在-7℃以下,夏季月平均气温在20℃以上。其气候特征可归纳为:冬季寒冷少雪,夏季温和多雷阵雨,气温年较差比较悬殊,寒潮较频繁,日较差明显。大坝多年平均气温和河水温度,见表1—2。
4 边界条件
坝体稳定温度场完全受边界温度控制,要准确地分析稳定温度场,首先必须准确地确定边界条件。
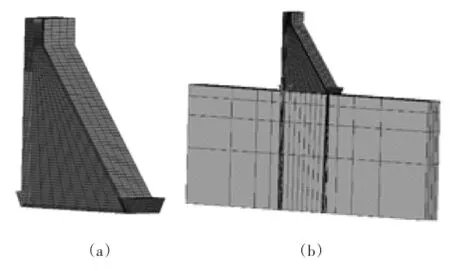
图6 大坝挡水坝段有限元模型
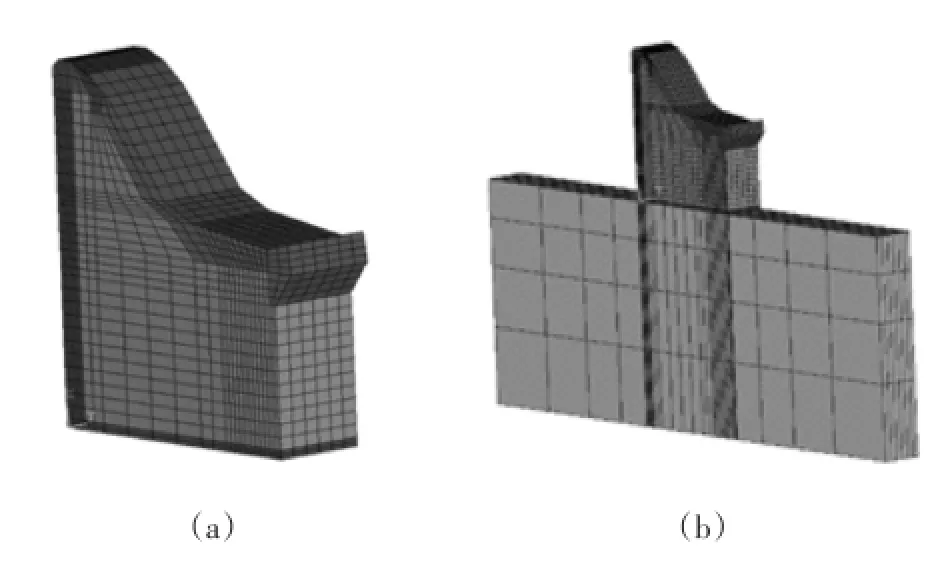
图7 大坝溢流坝段有限元模型

图8 大坝电站坝段有限元模型
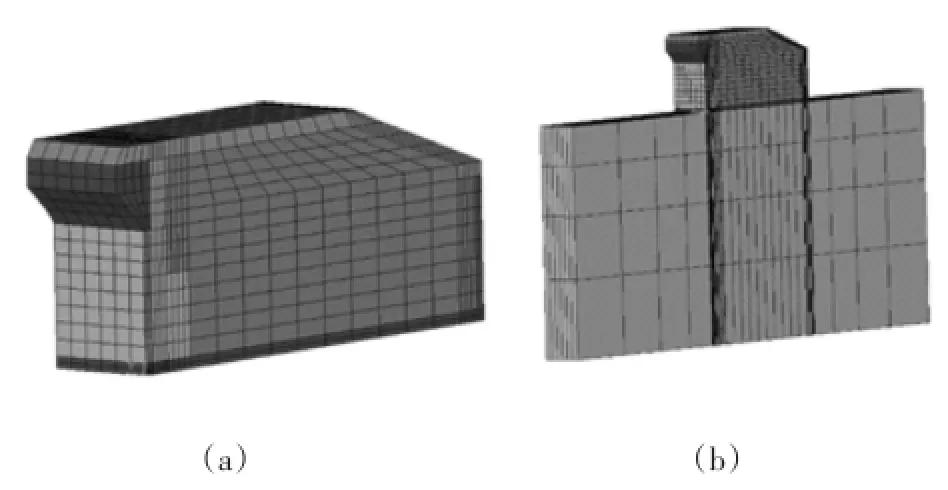
图9 大坝底孔坝段有限元模型
4.1库水温度表达式
影响水库水温的因素非常复杂,包括库容、库深、入库水量和水温、出库水量和泄水高程、水库的调节性能、当地的气温、日照、风速、进库水流的含砂情况等。确定库水温度的方法有:类比法,采用与拟建水库各方面条件相同或相似水库的水温实测资料作为新建水库的水温;统计法,对国内外已建水库水温的实测资料进行统计和分析,找出规律,建立水库水温的计算公式;数值计算法,建立水库水温计算的物理模型和数学模型,用数值分析的方法进行计算,该方法要求的基本资料比较多,水库水温计算的精度取决于资料的准确性。本文采用水温统计的成果分析计算水库的水温。

表1 大坝坝址多年旬平均气温 ℃

表2 大坝坝址多年月平均水温 ℃
上游坝面库水温度的变化规律受大气温度变化规律的影响,水库某一点的温度变化可按下式计算:
式中:y为水深(m);τ为时间(月);T(y,τ)为τ时水深y处的水温(℃);Tm(y)为水深y处的年平均水温(℃);A(y)为水深y处的水温年变幅(℃);ω为温度周期变化的圆频率(ω=2π/P);ε为水温和气温变化的相位差(月),采用ε的目的是将水温和气温统一在同一个时间轴上;P为温度变化的周期(12个月)。
当τ=τ0时,气温最高,而水温比气温滞后ε,故当τ=τ0+ε时水温最高。一般气温以7月中旬为最高,故应取τ0=6.5月。需要注意的是,相位差ε随水深y变化。
由式(9)可见,对于某一水深y,只要确定了年平均水温Tm(y)、水温年变幅A(y)和相位差ε,则任意时间的水温皆可由该式算出。
4.2年平均水温
年平均水温Tm(y)随水深变化,可按下式进行计算:
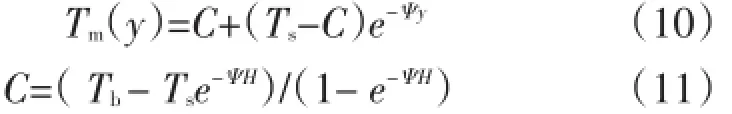
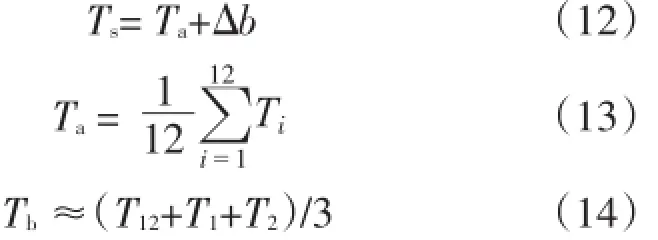
式中:Ts为水库表面年平均水温(℃);Ψ可取0.04;一般地区Ta为当地年平均气温(℃),冬季水库表面结冰的寒冷地区(年平均气温在10℃以下)Ta为当地年平均气温的修正值(℃);Ti为第i月的月平均气温(℃),当Ti<0时,取Ti=0;Δb为由于日照影响的温度增量(℃),约0~4℃,在冬季水库表面结冰的寒冷地区(年平均气温在10℃以下),可取2℃;Tb为库底年平均水温(℃),T12、T1、T2分别为12月、1月、2月的月平均气温(℃),Tb在一般地区等于气温最低的3个月份(12月、1月、2月)的平均气温,在寒冷地区约等于4~6℃,取Tb=6℃;H为水库水深(m);其他变量含义同前。
根据水库坝址的气温和工程情况,水库水温的计算结果见表3。

表3 水库水温的年平均温度随水深的变化
4.3水温年变幅
根据国内外一些水库的实测资料,任意水深的水温年变幅A(y)可按下式计算:

寒冷地区,则:

式中:T7为当地7月的月平均气温(℃);η可取0.018;Δα可取2℃;A0为水库表面水温年变幅(℃);其他变量含义同前。
在该坝区,A0=0.5T7+Δα=0.5×23.64+2=13.82(℃)。
经计算,得出水温年变幅,见表4。

表4 水温年变幅
4.4水温相位差
水温相位差可按下式计算:
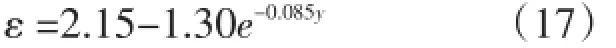
经计算,得出水温相位差,见表5。

表5 水温沿水深的相位差
4.5边界条件确定
温度场计算中绝热边界为地基底面、地基的4个侧面、坝段横缝及坝段厚度中截面。蓄水前坝体上下游面视为第3类边界(坝面与空气接触)。蓄水后水面以上为第3类边界,水面以下如不贴保温板,则按第1类边界处理,如贴保温板则按第3类边界处理。
上游水位取正常蓄水位,与水接触的坝面温度等于年平均水温;下游取设计尾水位,水温取值为多年平均河水水温,太阳辐射的影响取值为2℃,与空气接触的坝面温度Ts取值为年平均气温与太阳辐射的影响之和,则坝面温度Ts=8.6+2=10.6(℃)。
5 稳定温度场计算结果分析
前述4个典型坝段的稳定温度场等值线,如图10—14所示。
Simulation and Calculation of Stability Temperature Field of a Roller Compacted Concrete Dam in Cold Region
ZHANG Jun-xia1,ZHANGHao2
(1.Water Information Network Center,HaiheRiver Basin Commission,Tianjin 300170,China;2.HeBeiResearch Instituteof Investigation&Design ofWater Conservancy&Hydropower,Tianjin 300250,China)
There isa roller compacted concrete dam in north cold area,in which thewinter temperature is low,the summer temperature is high,the amplitude of temperaturewithin a year is large,the amplitude of temperaturewithin a day is large too,the cold is frequently and the coolingamplitude is large.The dam temperature controland crack prevention isextremely unfavorable.In order to study the distribution of concrete dam temperature stressand then put forward to the temperature control standardsmeeting the temperature control and crack prevention and the corresponding prevention measures,the concreteof typicaldam section,typicaloverflow dam section,typical power diversion dam and typical dam section is selected as the research object.With the heat conduction theory and finite elementmethod,the temperature field is simulated using the resultsofwater temperature statistics.The resultsshow that the stability of the dam temperature isabout7 to9℃.
cold area;roller compacted concrete dam;temperature field;simulation;finiteelement
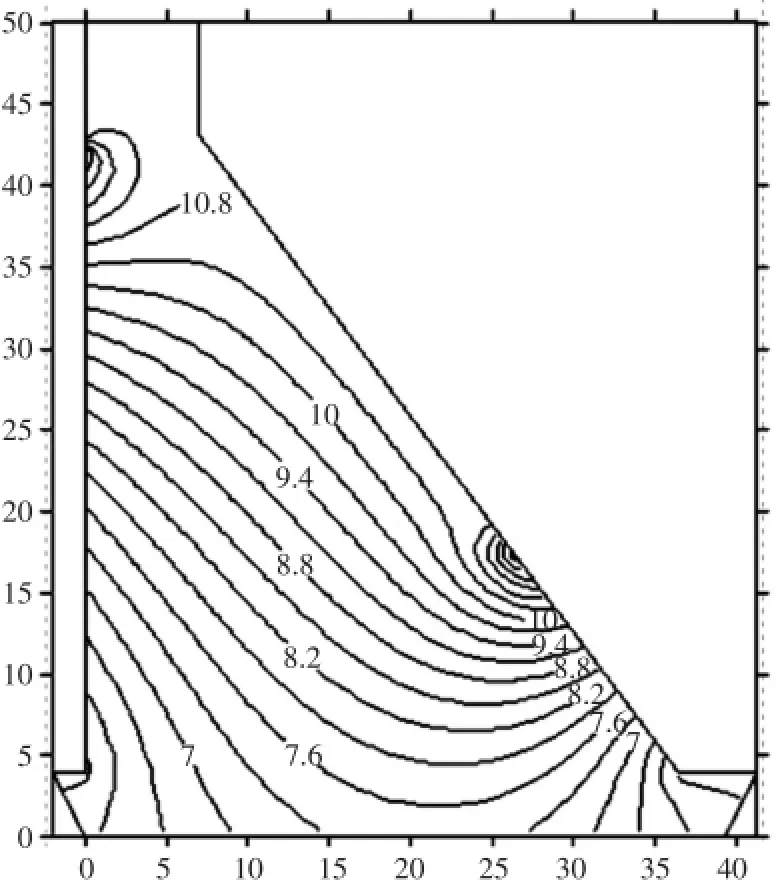
图10 大坝挡水坝段稳定温度场等值线/℃
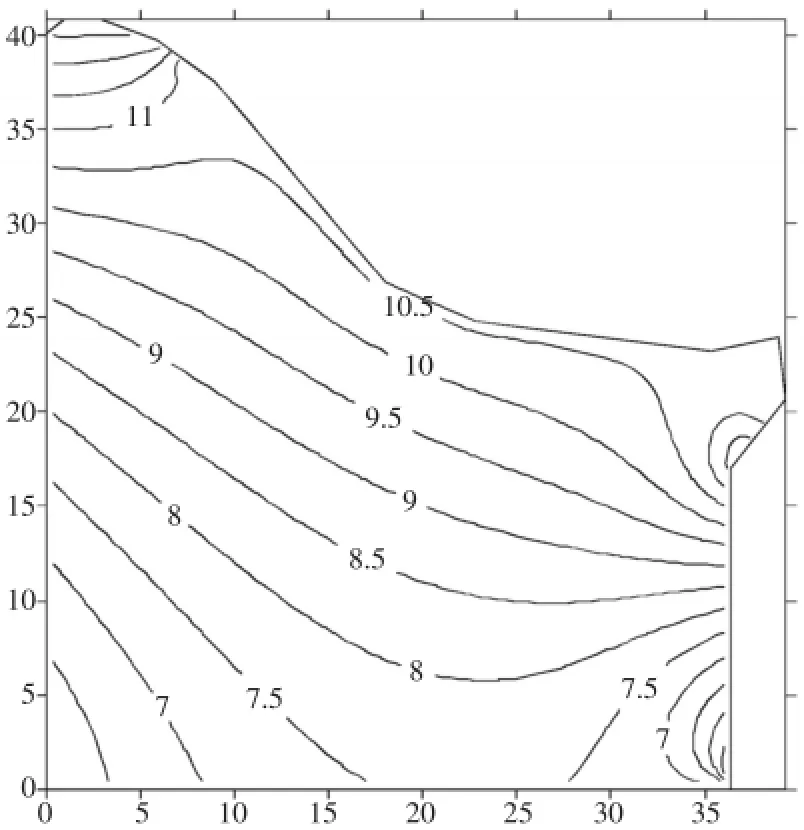
图11 大坝溢流坝段稳定温度场等值线/℃
TV642.2;TV314
A
1004-7328(2016)05-0055-06
10.3969/j.issn.1004-7328.2016.05.019
2016—07—12
张俊霞(1975—),女,高级工程师,主要从事水利信息技术及水利科技期刊编辑出版工作。
