一种基于蒙特卡罗模拟的发震概率计算方法*

郭　星　潘　华

1) 中国北京100082环境保护部核与辐射安全中心2) 中国北京100081中国地震局地球物理研究所



一种基于蒙特卡罗模拟的发震概率计算方法*

郭星1)潘华2),*

1) 中国北京100082环境保护部核与辐射安全中心2) 中国北京100081中国地震局地球物理研究所

针对大震发生概率计算过程中的不确定性，本文分别对不确定性及其处理方法进行了探讨． 考虑到不确定构成的复杂性，提出了一种基于蒙特卡罗模拟的大震发生概率计算方法, 并以东昆仑断裂带塔藏段为计算实例，利用蒙特卡罗法处理发震概率计算过程中的各种不确定性. 结果表明, 古地震数据的不完整性对计算结果的影响很大. 本文采用逻辑树法考虑古地震数据的不完整性，得到塔藏段未来100年的大震发生概率为0.12．

大震发生概率蒙特卡罗不确定性

引言

考虑到大地震的记忆性，Utsu(1972)，Rikitake(1974)和Hagiwara(1974)基于Reid(1910)提出的弹性回跳理论，提出了一种更新模型，该模型假定断层上大地震的复发符合更新过程． 国外研究人员先后提出了多种概率分布来描述这种更新模型，具体的概率分布模型包括高斯分布(Rikitake，1974)、韦布尔分布(Hagiwara，1974)、对数正态分布(Nishenko，Buland，1987)、布朗过程时间(Brownian passage time，简写为BPT)分布(Ellsworthetal，1999； Matthewsetal，2002)等模型．

对于任何一种概率分布模型，若已知大震复发的概率密度函数f(T)和最近一次大震的离逝时间Te，则可利用下式计算断层源在未来一段时间ΔT内发生大震的条件概率(Wesnousky，1986)：

(1)

不确定性一般可分为认知不确定性和随机不确定性，本文在此基础上又对不确定性的定量化过程和处理过程分别进行了深入分析． 按照概率分布类型不同，将不确定性分布分为连续型分布和离散型分布; 按照认知主体的不同，将不确定性的处理分为对个体自身认知不确定性的处理和对不同个体之间认知差异性的处理． 最后进一步探讨了具体的不确定性处理方法和原则．

此外，大震发生概率计算过程中的不确定性构成往往很复杂，例如，不确定性因素较多，而不同不确定性因素之间又存在相关性，这使得利用数值方法实现起来比较困难． 针对该问题，本文首先提出利用蒙特卡罗模拟法对大震发生概率模型中的各种不确定性分布直接进行反复随机抽样； 然后，通过对大量的随机模拟结果进行统计分析，得到最终的大震发生概率计算结果； 最后，以东昆仑断裂带塔藏段的大震发生概率为计算实例，在充分考虑各种不确定性的基础上，建立了塔藏段的大震发生概率模型，并利用蒙特卡罗法计算塔藏段未来100年的大震发生概率．

1　大震发生概率模型的不确定性分析

1.1不确定性分类

在各种地震危险性模型中，对于不确定性的划分，一般可分为随机不确定性和认知不确定性(Bommer，2003)． 随机不确定性反映的是自然本身所固有的各种随机性； 认知不确定性反映的是基于不完备的信息和知识，人的主观认知和判断的不准确性．

大震危险性分析中的不确定性分析是对不确定性进行定量化处理，进而在大震危险性分析中考虑各种不确定性因素． 随机不确定性和认知不确定性有时可以分离，有时则很难分离． 因此，为了探讨不确定性的具体处理方法，本文在不确定性处理过程中，分别按照概率分布类型的不同和认知主体的不同进行划分，而未将随机不确定性和认知不确定性分离开进行讨论．

首先，按照概率分布类型不同，本文将不确定性分布分为连续型分布和离散型分布． 对于不确定性的定量化描述，根据具体情况的不同，可以采用连续型分布，也可以采用离散型分布． 其中，连续型分布更为客观，但建立相对可靠的分布模型需要足够的样本支持，同时连续型的概率分布不方便计算； 离散型分布的确定相对主观，但却便于计算． 其次，按照认知主体的不同，本文将不确定性的处理分为对个体自身认知不确定性的处理和对不同个体之间认知差异性的处理． 在不确定性的实际处理中，不仅要考虑研究个体，同时还需考虑不同研究人员之间所得出的不确定性定量化结果的差异性(SeniorSeismicHazardAnalysisCommittee，1997)． 这种差异性反映的是人与人之间存在的认知分歧，为了避免计算结果过于主观和片面，需要在大震危险性分析中考虑这种分歧．

图1　不确定性的处理过程Fig.1　The process of uncertainty

1.2不确定性的处理方法

为便于讨论不确定性的具体处理方法，根据本文所采用的分类方式，并参考前人在概率地震危险性分析中不确定性处理方面的研究成果(Senior Seismic Hazard Analysis Committee，1997)，本文对不确定性的处理过程参见图1.

1.2.1采用连续型分布来定量化不确定性

连续型分布较离散型分布更为精确，但其计算量较大，因此如果计算条件允许，可以采用连续型分布来定量化不确定性． 连续型分布的具体分布形态又分为均匀分布和非均匀分布．

1) 均匀分布. 客观信息量越少，不确定性越大，这是个不变的原则，必须体现在大震危险性分析中的每个具体环节中． 对于基本不可知因素或完全不可知因素的不确定性评价，一般采用均匀加权法，其本质上属于拉普拉斯决策法，即等可能决策法． 均匀分布在实际地震危险性分析中应用广泛，例如： 在潜在震源区内任何地方发生地震的可能性是相同的(Cornell，1968)； 古地震发生在其年代测定不确定性的上下限内任意一年的可能性也是相同的．

2) 非均匀分布. 若要用非均匀分布来表示不确定性，首先必须假设一个非均匀分布模型，然后通过参数估计法确定该分布模型的参数． 具体的参数估计法包括矩估计、最大似然估计、贝叶斯估计等． 其中矩估计和最大似然估计多用于计算某些自然随机分布的参数，而贝叶斯估计则多用于计算某些模型参数的认知不确定性分布． 如果有连续性的证据或数据，则可以采用非均匀分布来表示不确定性，但必须先定义一个分布模型，甚至是出于个体的主观认识．

1.2.2采用离散型分布来定量化不确定性

逻辑树是一种常用的离散化不确定性处理方法． 该方法一般分为两种： 一种是加权逻辑树法，一种是不加权逻辑树法．

1) 不加权逻辑树． 对于个体的认知不确定性处理，类似于连续型分布中的均匀分布，不加权逻辑树也是一种等可能加权． 对于不同个体之间的认知不确定性的差异性处理，可以采用不加权逻辑树，这意味着在决策过程中不同个体的认知被赋予相同的权重，即不同个体之间是平等的．

2) 加权逻辑树． 利用加权逻辑树对个体认知不确定性的处理，是单独地研究个体基于有限的地震地质资料和信息，对大震危险性评估过程中某个环节的认知不确定性分布所作的离散处理，其中每个逻辑树分支均被主观地赋予一定的权重． 根据有限的地震地质资料和信息，对两种或两种以上可能(或离散型的参数值)的权重进行主观评定． 最终评定结果的确定须参考信息的完备程度，信息量越少，未知因素越多，不确定性也就越大． 例如，某个不确定性环节包括A和B两种可能，即使所有的已知信息均支持A，但如果信息量非常有限，也不可以给出确定的结论，而应参考信息量的完备程度，在充分考虑不确定性的基础上进行权重评估．

对于个体之间的认知不确定性的差异性处理，也可以采用加权逻辑树法，其综合了不同个体认知的权重不平等性和单独个体的认知不确定性． 此外，在不确定性处理过程中还需注意以下两点：

1) 必须保证权重赋予和不确定性分布范围确定过程的一致性原则． 一个独立的人或者独立的小组，在大震危险性评估过程中每个具体的不确定性环节，必须遵循相同的不确定分级原则或权重分配原则．

2) 在评估不确定性分布范围的过程中，需要保守考虑，但又不可以无限地保守． 一些概率极低的极端事件对计算结果的贡献很小，也很难进行概率评估和计算，所以，在实际大震危险性评估过程中可以对不确定性分布作适当的截断处理．

2　计算实例

本文以东昆仑断裂带东段塔藏段的大震发生概率为计算实例，具体研究在大震发生概率计算过程中如何考虑不确定性．

2.1东昆仑断裂带塔藏段的古地震

东昆仑断裂带东段位于巴颜喀拉地块与西秦岭地块边界断裂的东段，全长约330 km，自西向东可划分为3段： 玛沁段、玛曲段和塔藏段(青海省地震局，中国地震局地壳应力研究所，1999)． 国内外研究人员在东昆仑断裂带东段上获得了许多古地震数据，为评估该段的大地震发生概率提供了重要依据． 其中，玛沁段和玛曲段上的古地震数据比较丰富，而塔藏段上的古地震数据量则比较少，完整性较差，最近一次大震的离逝时间也存在很大的不确定性．

根据李正芳等(2012)对前人古地震研究结果的分析，本文给出了塔藏段古地震的发生时间分别为距今(4693±151)年，(7304±500)年和(9136±131)年，其中存在4700年左右的大地震空白期，很可能存在历史地震漏记的现象． 另根据李正芳等(2012)对四川松潘(位于塔藏段东南方向约50 km)历史文献记载的分析，推断塔藏段最近一次地震的发生时间应在公元638年之前，即最近一次地震的离逝时间应介于1377—(4693±151)年之间．

2.2不确定性分析

由于塔藏段古地震数据量比较少，完整性较差，不管是大震复发间隔还是大震离逝时间，均存在着非常大的不确定性． 具体的不确定性因素包括以下3个方面：

1) 在离逝时间Te的确定过程中，需要考虑古地震记录和历史地震记载的不完整性所造成的最近一次大地震发生年代的不确定性.

首先，古地震的完整性研究一直是古地震研究的难题，不同断裂上的古地震研究深度不同，地层的完整性情况也不同，造成不同断裂和不同时段的古地震记录的完整性情况相差较大(冉勇康，邓起东，1999)； 其次，我国历史地震资料保存得相对较多，但就各个历史时期和不同区域来说，历史地震记载的完整性程度相差较大(陈春梅，任雪梅，2014)． 因此，无法通过客观的统计分析方法得到最近一次大地震发生时间的不确定性分布，也无法直接判定某时间段内的大震记录是否完整或缺失的数量，只能主观评估已知信息量能否足够(或充分)判定给定时间段的大地震记载是完整的．

本文提出采用逻辑树法来分析由古地震记录和历史地震记载的不完整性所造成离逝时间Te的认知不确定性． 逻辑树在此处共有两个分支： ① 根据已知的区域古地震研究成果和区域历史地震记载情况，无法确定给定时间段的大地震记载是完整的，即信息量有限，无法得出确定性的结论； ② 根据已知的区域古地震研究成果和区域历史地震记载情况，可以确定给定时间段的大地震记载是完整的，即信息量是足够充分的，可以得出确定性的结论． 根据已知的数据和资料，并征求相关方面专家的意见，对两个逻辑树分支的权重进行主观赋值．

2.3考虑不确定性的塔藏段大震发生概率计算模型

在Reid(1910)弹性回跳理论的基础上，国内外研究人员先后提出了多种符合更新过程的概率模型，其中比较常用的概率分布模型有对数正态分布模型(Nishenko，Buland，1987)、BPT(Ellsworthetal，1999； Matthewsetal，2002)模型等．

本文未考虑模型本身的不确定性，直接采用BPT模型计算大震发生概率. BPT分布也被称作逆高斯分布(Seshadri，1983)，其概率密度函数为

(2)

参考对不确定性处理方法的分类讨论，本文采用加权逻辑树法来考虑古地震的不完整性． 考虑到每个逻辑树分支所对应的计算过程均存在一定差异，本文分成A 和B两个相互独立的蒙特卡罗模拟过程分别进行计算． 其中分支A假定根据有限的信息，无法确定给定时间段的大地震记载是完整的； 分支B假定信息量足够充分，可以确定给定时间段的大地震记载是完整的． 根据已知的数据和资料，并征求相关方面专家的意见，对两个逻辑树分支的权重进行主观赋值．

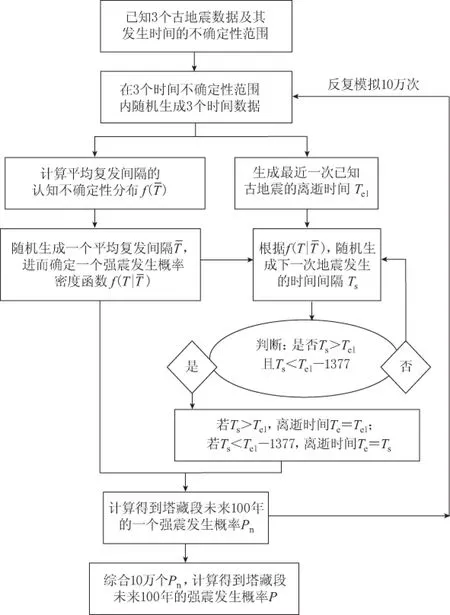
图2　塔藏段大震发生概率计算的分支A流程图Fig.2　The process chart of branch A for calculating the occurrence probability of large earthquakes on the Tazang fault

分支A的具体实现步骤如图2所示：

(3)

而复发间隔为T22的概率密度函数为

(4)

(5)

(6)

从保守和计算效率的角度考虑，判定过程中并未考虑记载空段内漏记两次或两次以上古地震的小概率特殊事件的发生．

图3　塔藏段大震发生概率计算的分支B流程图Fig.3　The process chart of branch B for calculating the occurrence probability of large earthquakes on the Tazang fault

6) 反复模拟10万次，计算出10万次模拟结果的平均值P．

分支B的具体实现步骤与分支A类似(图3)，只是第4步有所差异，考虑到分支B假定不可能出现古地震漏记，则直接取大震离逝时间Te=Te1．

2.4大震发生概率计算结果

分支A的大震发生概率计算结果为0.11； 分支B的大震发生概率计算结果为0.16． 而对于A和B两个逻辑分支的权重赋值则需要综合考虑以下几个方面： ① 研究区域的人类活动历史和历史地震记载的完整性情况； ② 研究断裂上的地层完整性情况； ③ 研究断裂上的古地震研究深度．

基于上述3个方面的信息，并征求相关方面专家的意见，本文给出的A和B两个逻辑分支的权重赋值WA和WB分别为0.8和0.2，最后计算出的塔藏段未来100年的大震发生概率为

P=PAWA+PBWB=0.11×0.8+0.16×0.2=0.12.

(8)

3　讨论与结论

本文对大震发生概率评估过程中的各种不确定性进行了系统分析，在认知不确定性和随机不确定性的基础上对不确定性的定量化处理过程进行了分类研究，并对不确定性的具体定量化方法进行了梳理．

考虑到大震复发概率计算过程中存在大量的不确定性，且不确定性的构成又较为复杂，数值方法实现起来比较困难，故此类不确定性往往被忽略掉． 本文首先明确了大震复发概率模型中的各种不确定性，特别是常被忽略的不确定性，然后利用蒙特卡罗模拟法对大震发生概率模型中的各种定量化的不确定性直接进行随机抽样，最后通过对大量随机模拟结果的统计分析得到了最终的大震发生概率计算结果． 虽然计算过程相对复杂，但可以尽可能地减少一些主观因素，使得计算结果更为客观．

本研究的重点在于探讨如何利用蒙特卡罗法考虑发震概率计算过程中的各种不确定性，对于各个不确定性分支的具体赋值过程则未进行更深入的研究． 而不确定性分支的权重将直接影响最终的计算结果，需要作大量的地震地质调查和统计分析工作，也需要采取科学有效的方法对多位专家的意见进行综合． 在实际大震危险性评估中，怎样考虑和处理这种人与人之间的认知分歧，也需进一步研究．

陈春梅，任雪梅. 2014. 我国大陆5个地区历史地震资料记载的完整性分析与比较[J]. 防灾减灾学报，30(2): 66--70.

Chen C M，Ren X M. 2014. Integrity analysis and comparison of five regional historical earthquake records in mainland China[J].JournalofDisasterPreventionandReduction，30(2): 66--70 (in Chinese).

郭星，潘华. 2015. 强震复发间隔变异系数的一种计算方法[J]. 地震学报，37(3): 411--419.

Guo X，Pan H. 2015. A method for computing the aperiodicity parameter of the strong earthquake recurrence interval[J].ActaSeismologicaSinica，37(3): 411--419 (in Chinese).

郭星，潘华. 2016. 强震复发概率模型中的参数不确定性研究[J]. 地震学报，38(2): 298--306.

Guo X，Pan H. 2016. Parameter uncertainty analysis on probability model of strong earthquake recurrence[J].ActaSeismologicaSinica，38(2): 298--306 (in Chinese).

李正芳，周本刚，冉洪流. 2012. 运用古地震数据评价东昆仑断裂带东段未来百年的强震危险性[J]. 地球物理学报，55(9): 3051--3065.

Li Z F，Zhou B G，Ran H L. 2012. Strong earthquake risk assessment of eastern segment on the East Kunlun fault in the next 100 years based on paleo-earthquake data[J].ChineseJournalofGeophysics，55(9): 3051--3065 (in Chinese).

毛凤英，张培震. 1995. 古地震研究中的逐次限定法与新疆北部主要断裂带的古地震研究[G]∥活动断裂研究(4). 北京: 地震出版社： 153--164.

Mao F Y，Zhang P Z. 1995. Progressive constraining method in paleo-earthquake study and the research on paleo-earthquakes along the major active faults in northern Xinjiang[G]∥ResearchonActiveFault(4). Beijing: Seismological Press: 153--164 (in Chinese).

青海省地震局，中国地震局地壳应力研究所. 1999. 东昆仑活动断裂带[M]. 北京: 地震出版社： 1--186.

Earthquake Administration of Qinghai Province，Institute of Crustal Dynamics，China Earthquake Administration. 1999.EastKunlunActiveFaultZone[M]. Beijing: Seismological Press： 1--186 (in Chinese).

冉勇康，邓起东. 1999. 古地震学研究的历史、现状和发展趋势[J]. 科学通报，44(1)： 12--20.

Ran Y K，Deng Q D. 1999. History，status and trend about the research of paleoseismlogy[J].ChineseScienceBulletin，44(10)： 880--889.

Bommer J J. 2003. Uncertainty about the uncertainty in seismic hazard analysis[J].EngGeol，70(1/2): 165--168.

Cornell C A. 1968. Engineering seismic risk analysis[J].BullSeismolSocAm，58(5): 1583--1606.

Ellsworth W L，Matthews M V，Nadeau R M，Nishenko S P，Reasenberg P A，Simpson R W. 1999.APhysically-BasedEarthquakeRecurrenceModelforEstimationofLong-TermEarthquakeProbabilities[R]. Reston，Virginia: US Geological Survey Open-File Report： 99--522.

Hagiwara Y. 1974. Probability of earthquake occurrence as obtained from a Weibull distribution analysis of crustal strain[J].Tectonophysics，23(3): 313--318.

Matthews M V，Ellsworth W L，Reasenberg P A. 2002. A Brownian model for recurrent earthquakes[J].BullSeismolSocAm，92(6): 2233--2250.

Nishenko S P，Buland R A. 1987. A generic recurrence interval distribution for earthquake forecasting[J].BullSeismolSocAm，77(4): 1382--1399.

Reid H F. 1910.TheMechanicsoftheEarthquake，TheCaliforniaEarthquakeofApril18，1906[R]. Washington，DC: State Earthquake Investigation Commission: 43--47.

Rikitake T. 1974. Probability of earthquake occurrence as estimated from crustal strain[J].Tectonophysics，23(3): 299--312.

Senior Seismic Hazard Analysis Committee. 1997.RecommendationsforProbabilisticSeismicHazardAnalysis:GuidanceonUncertaintyandUseofExperts[R]. Washington，DC: US Nuclear Regulartory Commission: 1--256.

Seshadri V. 1983. The inverse Gaussian distribution: Some properties and characterizations[J].CanadianJStatist，11(2): 131--136.

Utsu T. 1972.LargeEarthquakesNearHokkaidoandtheExpectancyoftheOccurrenceofALargeEarthquakeOffNemuro[R]. Hokkaido: Coordinating Committee for Earthquake Prediction: 7--13.

Wesnousky S G. 1986. Earthquakes，Quaternary faults，and seismic hazard in California[J].JGeophysRes，91(B12): 12587--12631.

A method for calculating occurrence probability of large earthquakes based on Monte Carlo simulation

Guo Xing1)Pan Hua2),*

1)NuclearandRadiationSafetyCenter，MinistryofEnvironmentProtection，Beijing100082，China2)InstituteofGeophysics，ChinaEarthquakeAdministration，Beijing100081，China

According to the uncertainty in the process of calculating the occurrence probability of large earthquakes，a study is made on uncertainty and its dealing methods. Considering the complexity of uncertainty，this paper presents a method for calculating the occurrence probability of large earthquakes based on Monte Carlo simulation. With the Tazang segment of eastern Kunlun fault zone as an example，we deal with different kinds of uncertainties in calculating the occurrence probability of large earthquakes using Monte Carlo method. The result shows that the incompleteness of paleo-earthquakes data has great effect on the calculation result. With the logical tree to deal with the incompleteness of paleo-earthquakes data，the occurrence probability of large earthquakes is 0.12 in the next 100 years on the Tazang segment.

large earthquake； occurrence probability； Monte Carlo； uncertainty

国家科技支撑项目(2012BAK15B01-08)资助.

2016-03-01收到初稿，2016-07-18决定采用修改稿.

e-mail: panhua.mail@163.com

10.11939/jass.2016.05.012

P315.5

A

郭星，潘华. 2016. 一种基于蒙特卡罗模拟的发震概率计算方法. 地震学报, 38(5): 785--793. doi:10.11939/jass.2016.05.012.

Guo X, Pan H. 2016. A method for calculating occurrence probability of large earthquakes based on Monte Carlo simulation.ActaSeismologicaSinica, 38(5): 785--793. doi:10.11939/jass.2016.05.012.