矿区深部隐伏矿体三维可视化预测方法

毛先成， 张苗苗， 邓　浩， 邹艳红， 陈　进

(1.有色金属成矿预测与地质环境监测教育部重点实验室，湖南长沙410083； 2.中南大学地球科学与信息物理学院，湖南长沙410083)



矿区深部隐伏矿体三维可视化预测方法

毛先成1,2， 张苗苗1,2， 邓浩1,2， 邹艳红1,2， 陈进1,2

(1.有色金属成矿预测与地质环境监测教育部重点实验室，湖南长沙410083； 2.中南大学地球科学与信息物理学院，湖南长沙410083)

针对深部隐伏矿定位难题，经多年研究，提出以定位模型-成矿信息-三维预测为主线的隐伏矿体三维可视化预测方法。矿体定位概念模型实现成矿规律到矿化分布规律的转换，获得矿体空间定位量化指标；采用形态分析、距离场或缓冲区分析、蚀变场分析等空间分析方法，分析和定量提取成矿信息指标；采用非线性多元回归、三维模糊证据权等方法，建立矿体三维预测模型，对深部立体单元的品位、金属量和含矿性进行预测。以安徽铜陵凤凰山铜矿和金川铜镍硫化物矿床为例，展开矿区深部三维可视化预测研究。结果显示，该方法能够适用于不同类型矿床的深部找矿工作，对于深部找矿具有重要意义。

隐伏矿体；定位概念模型；成矿信息；三维可视化预测；安徽铜陵；甘肃金川

0　引　言

随着经济和社会的发展，人类对矿产资源的需求量日益增加，同时易于找寻的露头矿、近地表矿日趋减少,一批20世纪五六十年代建设投产的大中型矿山保有储量逐渐枯竭，多数已进入危机矿山行列。通过对国内外矿山的勘探情况和现行探采技术分析，我国大多数矿山深部仍具有巨大的找矿潜力(赵鹏大等，2004)，因此寻找深部第二成矿空间成为促进矿山找矿工作新突破的重要途径。

矿产资源定量评价始于20世纪50年代(Allais，1957)，经历了起步、发展、成熟等阶段后，目前已进入科学化、定量化和数字化阶段。在起步和发展阶段，各国进行了广泛、大量的预测评价理论方法研究和应用(Harris,1969；Sinclair et al., 1970；Agterberg, 1971)，矿产资源定量预测与评价逐步趋于完善和实用，突出性代表成果是：国际地科联IGCP98专题推出的6种矿产资源定量预测方法，国内外通用的矿床统计预测理论及方法(赵鹏大等，1994；Agterberg，1974；Zhao，1992)，美国地质调查局提倡的“三步式”资源评价法(Singer，1993)，我国学者提出的综合信息预测(王世称等，1989，2000)和地质异常致矿理论(赵鹏大等，1991，1993)。

20世纪90年代，随着GIS相关理论及方法的蓬勃发展，GIS技术在地学领域的广泛应用，形成了以空间数据库和GIS空间分析为技术支撑、以多元地学空间数据集成-多元成矿信息提取与融合-矿产资源潜力制图为核心流程的矿产资源数字化预测评价体系(肖克炎等，2000；叶天竺等，2007；Agterberg et al.，1993；Bonham-Carter et al.，1995；Harris et al.，2000，2007；Asadi et al.，2001；Kemp et al., 2001；Porwal et al., 2010)，其理论和方法已成为目前开展矿产资源预测与评价的主流方法，广泛应用于区域矿产资源远景预测评价工作中。

然而，上述矿产资源定量评价方法的形成和发展主要源于中小比例尺的全球性和区域性矿产预测评价，工作范围大多属于2维或2.5维，因此难以适应和满足大型矿山可接替资源找矿向深边部三度空间发展的要求。为了将矿产资源定量评价理论和方法有效地应用于大型矿山深部找矿预测，需要在上述理论和方法的基础上，发展真三维的三维地质建模、空间分析和非线性预测技术，以达到矿山深部的隐伏矿体立体定位定量预测要求。三维地质建模技术的日臻成熟与实用(Houlding，1992，1994)，为矿产资源定量评价的三维化奠定了技术基础。目前，基于三维地质建模技术的三维成矿预测方法正在逐步发展成为深部资源的关键技术与方法(陈建平等，2007；毛先成等，2010；肖克炎等，2012；袁峰等，2014)。

针对矿山深部隐伏矿体立体定位定量预测的要求，在以往研究积累(毛先成等，1988a，1988b；毛先成，2006)的基础上，提出基于三维地质建模和三维空间分析的矿区深部隐伏矿体三维可视化预测方法与技术框架。此方法已在安徽铜陵凤凰山铜矿、福建丁家山铅锌矿床、山东大尹格庄金矿和夏甸金矿、广西田林—大新锰矿、甘肃金川铜镍矿深部找矿预测工作中得到了应用，并取得了良好的效果。

1　方法与模型

为实现矿区深部隐伏矿体三维可视化预测，首先要实现地质数据集成和成矿规律分析，形成地质数据库及矿体定位概念模型，分别为预测提供数据和知识驱动。基于已建地质数据库，利用三维地质建模技术建立三维地质体模型；在成矿概念模型指导下，基于三维地质体模型，采用三维地质体形态分析、距离场分析等空间分析技术定量提取成矿信息，分析成矿信息和矿化分布间的关联关系；最终构建反映找矿变量到矿化变量映射关系的三维预测模型，实现对预测区三维空间中矿化分布的三维定量预测。

1.1矿体定位概念模型

矿体定位概念模型实现矿床对象的成矿环境、成矿规律到矿化分布规律的转换，指导三维成矿信息分析和矿体空间定位量化指标提取，为矿区深部隐伏矿体三维可视化预测提供知识驱动。依据矿床的成矿模式和成矿规律，分析控矿地质条件和矿化富集规律，归纳矿体定位规律，形成矿体定位概念模型。成矿信息包括控制矿床矿体定位与分布的主要地质因素及相关地质体和找矿标志。表1所示概念模型列出了控制矿体空间定位的常见地质体与控矿因素及其分析方法和表达模型。

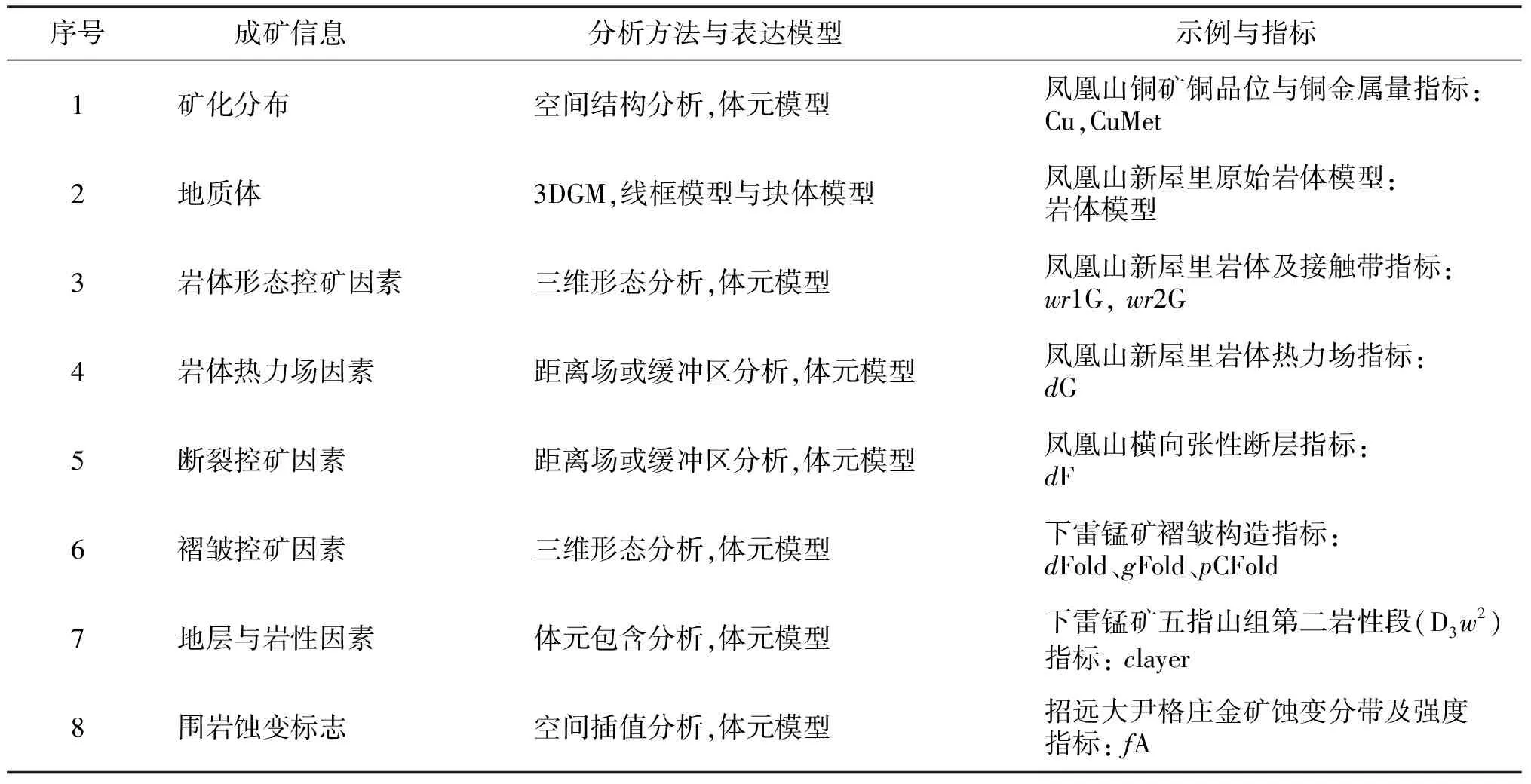
表1　矿体定位概念模型

1.2矿床三维地质建模

矿床三维地质模型是揭示地质体空间分布规律、实现成矿信息定量提取的前提和基础。现有的地质体三维模型构建方法主要是利用钻孔数据、勘探剖面、地震资料等数据进行三维建模，尤其是在研究程度较高的矿区，采用钻孔数据和勘探剖面进行地质体三维建模能实现对地质体表面形态和内部属性的精细表达。

三维地质体模型主要包括线框模型和块体模型，线框模型能直观地显示地质体三维形态，便于数据更新，但无法表示地质体内部属性，且不便于进行空间分析；块体模型则支持地质体内部属性描述和真三维表达。图1为新屋里岩体的线框模型和块体模型。

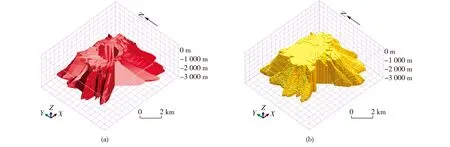
图1　新屋里岩体线框模型(a)和块体模型(b)Fig.1　Wireframe model (a) and block model (b) of the Xinwuli rock mass

1.3成矿信息三维空间分析

成矿信息三维空间分析的目的是提取可以用于指导找矿的空间信息(即成矿信息)。成矿信息的定量提取是以地质体三维模型为数据基础，以矿体的空间分布特征和成矿地质条件等地质知识和经验为指导，将定性的控矿因素进行定量表达，从统计角度分析地质因素对矿化空间分布的影响，从而为成矿预测模型的建立提供数据。

1.3.1地质体三维形态分析矿化空间分布通常在一定程度上受到相关地质体形态的影响和控制，本次研究采用空间分析的方法提取形态控矿指标(毛先成等，2010)。为了实现各类超覆、弯曲等复杂地质体的趋势、凹凸和起伏程度的定量提取，框架采用一种基于数学形态学与欧氏距离变换的地质体三维形态分析方法，具体步骤如下。

(1) 以A代表地质体对象，Bball代表球形结构元素(球体具有各向同性的特点),采用形态滤波对地质体进行滤波变换，获取平滑的趋势形态(图2)，变换后的地质体轮廓光滑程度取决于球形结构元素的半径，形态滤波变换可表达为：

开闭滤波：

ψ(A)=A∘Bball·Bball

(1)

闭开滤波：

ψ(A)=A·Bball∘Bball

(2)

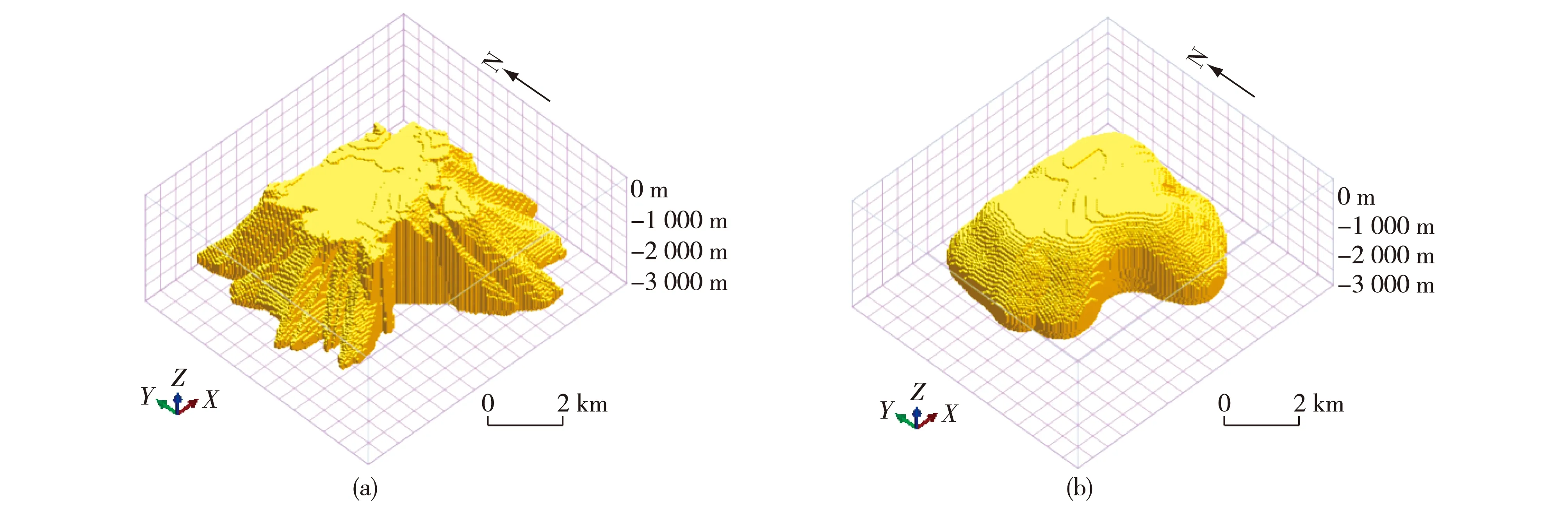
图2　新屋里岩体原始(a)和趋势形态(b)栅格模型Fig.2　Raster models of original (a) and trend shape (b) of the Xinwuli rock mass

(2) 通过对原始地质体A和趋势形态ψ(A)进行全局集合运算(式3、4)，可得到地质体的外凸部分集合Dpeak(A)和内凹部分集合Dvalley(A)，如图3所示。

凸部分：

(3)

凹部分：

(4)

图3　新屋里岩体外凸(a)和内凹(b)栅格模型Fig.3　Raster models for convex part (a) and concave part (b) of the Xinwuli rock mass

(3) 基于趋势-剩余分析方法的思想，在提取地质体趋势与凹凸部分的基础上，借助欧氏距离变换实现地质体表面起伏程度的定量提取。

在此基础上，为实现多个尺度下的定量分析，可以通过改变球形结构元素的半径，由上述步骤(1)—(3)完成多级形态指标的提取(图4)。

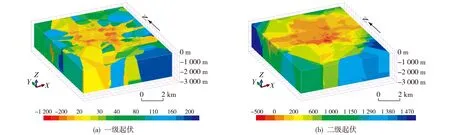
图4　新屋里岩体形态因素栅格模型Fig.4　Raster models showing morphological factors of the Xinwuli rock mass(a) first level undulation; (b) second level undulation

1.3.2控矿因素距离场分析地质体之间的距离或地质空间中某点到地质体的距离，可以表示地质体之间的空间临近性，并反映地质体对成矿空间中某点的影响(毛先成等，2010)。通过距离场分析，建立断层距离场、岩体热力场等场模型。将点到地质体的距离定义为两者之间的最近距离，选择欧氏距离作为控矿因素距离场的空间度量。

在基于栅格数据的空间分析中，立体单元到地质体的最近距离就是寻求立体单元中心到地质体块体距离集合的最小值，求取该距离最简单的方法是对空间中所有点进行距离量算，找出其中距离最小的点。当研究栅格数目十分巨大时，需要大量的距离量算，使得计算查找速度非常缓慢，但是，通过距离变换能够实现快速的距离量算。利用蔺宏伟等(2003)提出的三维带符号的欧氏距离变换(3-SEDT)算法来实现距离变换，以快速计算出每一个立体单元到地质体的最近距离，图5给出了安徽铜陵凤凰山横向张性断层因素和岩体热力场因素的栅格模型。

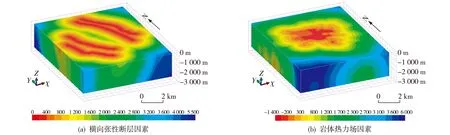
图5　凤凰山矿田控矿因素距离场Fig.5　Distance field of the ore-controlling factors in the Fenghuangshan ore field(a) transverse tensile fault factors; (b) thermal field factors of rock mass

1.3.3围岩蚀变的蚀变场强分析成矿过程伴随不同程度的围岩蚀变，因而蚀变带可在某种程度上反映矿体的空间分布规律，蚀变带场强反映了蚀变对矿化立体单元的影响程度。对于任意一个矿化立体单元Mi，它受到周围所有蚀变立体单元N的影响，这种影响程度的强弱受二者距离约束，因此可在一定的球形范围内，采用按距离加权的场来描述矿化立体单元的蚀变场指标。具体来说：设在一定范围内，有m个蚀变带立体单元，每个立体单元的蚀变场按照以下方法计算：(1) 矿化立体单元与蚀变立体单元重合，即该矿化立体单元为蚀变立体单元，场强为该立体单元的蚀变强度与周围加权蚀变场强的累加。(2) 未重合的立体单元直接按距离平方反比法，对其蚀变强度进行加权。

(5)

式(5)中，M1为矿化立体单元与蚀变立体单元重合立体单元，i1为矿化立体单元与蚀变立体单元重合立体单元的蚀变强度，j为缓冲区内蚀变立体单元编号，m为缓冲区内蚀变立体单元个数，ij为蚀变带立体单元的蚀变强度，N为缓冲区内所有蚀变立体单元集合，dj为矿化立体单元离蚀变带立体单元的欧氏距离。图6为大尹格庄金矿蚀变带场强因素模型。

图6　大尹格庄金矿蚀变带场强因素Fig.6　Field intensity factors of alteration zones in the Dayin′gezhuang gold deposit

1.4三维预测建模

预测模型可定量揭示地质空间中找矿指标与成矿信息之间的关联关系，另一方面，可以实现对研究区域内分布的隐伏矿体进行定位定量预测。矿化指标包括立体单元平均品位、金属量以及含矿性指标，由于含矿性指标在地质意义上是指在单元内找到工业矿体的概率，与品位及金属量指标计算方法不同，因此可分别建立不同的预测模型对立体单元的品位、金属量和含矿性指标进行估值预测。采用非线性多元回归模型建立品位及金属量预测模型，利用三维模糊证据权模型计算立体单元含矿性指标。

1.4.1非线性多元回归模型非线性多元回归模型通过描述体元的单个成矿信息与品位、金属量之间的关系，提取出与矿化指标呈线性关联关系的找矿信息指标，最后建立找矿指标与矿化指标间的多元线性回归模型。

成矿信息指标非线性变换方法为：(1) 计算地质空间范围内已知立体单元的矿化指标和成矿信息指标值，生成单个成矿信息指标与矿化指标关系的散点图；(2) 以散点图为依据，构建矿化指标与之间成矿信息指标的非线性变换的数学模型；(3) 根据非线性变换模型对成矿信息指标进行非线性变换，得到与矿化指标线性相关的新的找矿信息指标。

矿化指标与找矿信息指标的关联关系，在数学上可以表达为找矿信息变量空间到矿化变量空间的映射，其函数化表达模型为MV=f(GV)，MV为矿化变量空间，GV为找矿信息变量空间。由于找矿信息指标与矿化指标具有显著的线性相关性，所以该模型MV=f(GV)可以实例化为多元线性回归模型：

(6)

式(6)中，MVk为MV中的矿化变量，GVj为GV中的找矿信息指标，Bk0，Bk1，…，Bkp为线性函数的待求参数，ε为期望值为零的随机变量。参数Bk0，Bk1，…，Bkp可通过对GV和MV在地质空间控制区域中离散化单元的量化数据进行多元线性回归分析获得。

1.4.2三维模糊证据权模型三维模糊证据权模型是普通证据权的改进模型，它将传统二维证据权法扩展到三维空间中，并通过“模糊度”概念将原来二值化的证据因子变为一个模糊集合，该模型计算得到的后验概率可作为立体单元的含矿性指标。

假设地质空间包含n个等体积的立方体单元，其中有D个含矿单元，含矿单元赋值为1，不含矿单元赋值为0。假设共有n个证据因子，将证据因子Aj(j=1,2,3,…,n)的属性值分为mj个区间类，立体单元k的后验概率计算过程如下。

(1) 计算正、负权重值及差值C:

(7)

(8)

(2) 计算模糊权重值:

(9)

式中，j=1,2,3,…,n;t=1,2,3,…,mj;Ujt(x)通过对每一个证据因子的Cjt归一化求得。

(3) 计算后验概率。对于n个证据因子，研究区任一单元k为含矿单元的可能性优劣比的对数表示：

(10)

式(10)中，j=1,2,3,…,n;t=1,2,3,…,mj;k=1,2,3，…,n。立体单元k的后验概率P为：

(11)

2　应用实例

基于矿区深部隐伏矿体三维预测可视化方法，以安徽铜陵凤凰山铜矿和金川铜镍硫化物矿床为例，开展矿区深部三维可视化成矿预测研究。

2.1安徽铜陵凤凰山铜矿三维预测

安徽铜陵凤凰山铜矿是长江中下游多金属成矿带中典型的矽卡岩型铜矿矿床，位于新屋里岩体西部，矿区主矿体呈似板状和不规则透镜状产出于新屋里岩体与三叠系灰岩的接触带。众所周知，岩浆岩是矽卡岩型矿床中的重要成矿地质条件，新屋里岩体既是凤凰山铜矿的成矿母岩，又为成矿热液的运移提供持久的动力，还影响了局部应力场。构造条件上，矿区成矿作用受区域和局部应力场共同控制，尤其是岩浆上侵时形成的相关构造。接触带构造被认为是矿区最主要的控矿因素(刘亮明等，2008；瞿泓滢等，2010；彭省临等，2012)，但矿体就位也间接受到新屋里向斜、岩体侵位挤压形成的挤压褶皱构造和横向张性断层的控制。

基于安徽铜陵凤凰山矿田的矿体定位预测概念模型，以新屋里岩体三维模型作为分析的对象模型，利用上述三维成矿信息空间分析技术，定量提取成矿信息，描述这些控矿因素三维分布的场变量为：(1) 岩体热力场因素；(2) 岩体形态因素，即一级起伏和二级起伏；(3) 接触面构造因素，即原始接触面与趋势接触面的夹角；(4) 横向张性断层因素；(5) 挤压远应力场因素；(6) 褶皱构造因素。根据矿化指标和成矿信息的关联关系，建立该地区的三维预测模型。预测结果如图7，根据预测结果在凤凰山新屋里岩体西缘圈定深部找矿立体靶区。

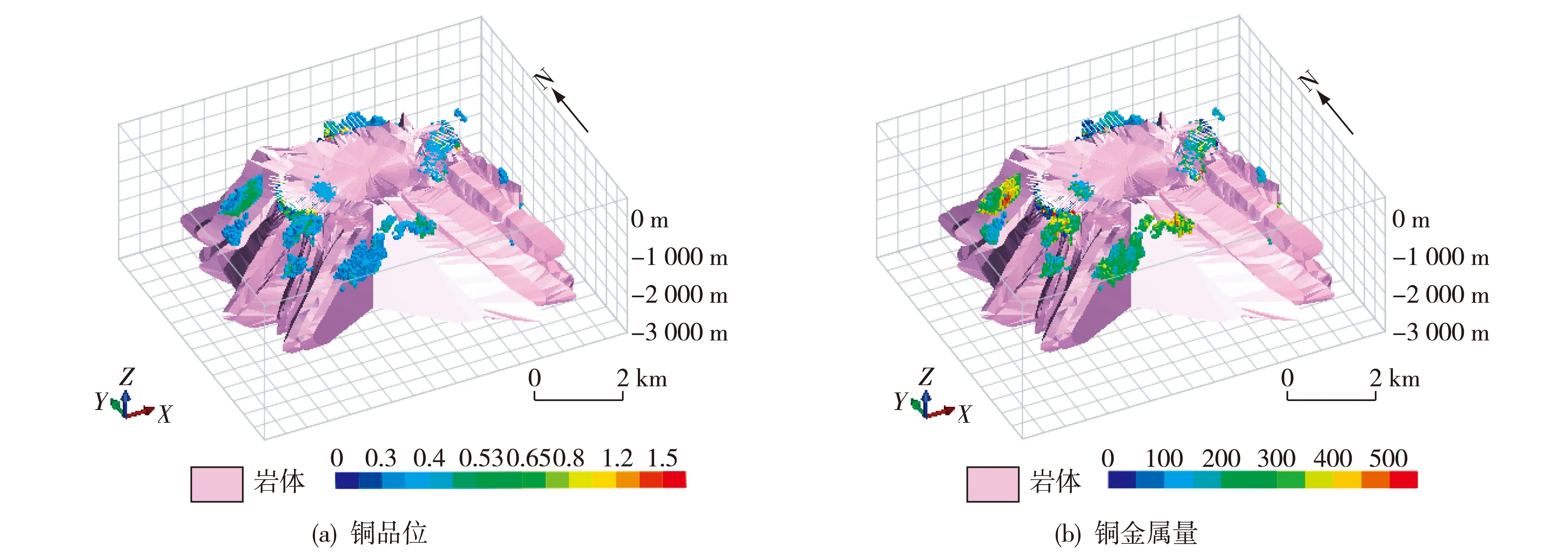
图7　安徽铜陵凤凰山矿田预测结果栅格模型Fig.7　Raster models showing prediction results of the Fenghuangshan ore field in Tongling, Anhui(a) copper grade; (b) copper metal quantity

2.2金川铜镍硫化物矿床三维预测

金川铜镍硫化物矿床位于华北板块龙首山隆起带，矿体产于基性—超基性岩墙中，属于古大陆内的小侵入体矿床(汤中立等，2007)。目前，金川矿床的成矿模式多被解释为岩浆通道系统成矿(田毓龙等，2009；苏尚国等，2010，2014；曾认宇等，2013a；Chen et al.,2013)，但岩浆通道系统成矿十分复杂，岩体侵位时，岩墙产状较缓，而岩体中存在的硫化物密度较大，在上升过程中受到重力分异的影响，故会向下富集，矿体尤其是富矿多集中在岩体的中下部，因此成矿不仅受到了岩浆本身影响，而且还与通道产状、形态、岩浆流速、重力分异等因素密切相关。另外，金川矿体最主要的控制因素是构造(曾认宇等，2013b)，特别是断裂，不仅控制了成矿作用，为矿体形成提供场所，还对已形成的岩体、矿体进行了改造。

根据金川铜镍硫化物矿床的成矿规律可知，矿体的空间分布主要受超基性岩体底板形态、顶底板相对距离、岩浆通道、断层等地质因素影响。在此基础上定量提取成矿信息，包括指标：(1) 岩浆通道中心线距离场；(2) 断层距离场；(3) 顶底板相对距离；(4) 底板趋势面距离场。利用多元线性回归模型和三维模糊证据权模型建立金川矿区预测模型，并对预测结果进行分析和可视化表达。预测结果如图8所示，根据预测结果并结合地质经验在金川矿区深部圈定有利找矿靶区。

3　结　论

(1) 针对深部隐伏矿定位难题，提出以定位模型-成矿信息-三维预测为主线的隐伏矿体三维可视化预测方法。

(2) 矿体定位概念模型实现成矿规律到矿化分布规律的转换，三维空间分析获得成矿信息定量指标，矿体三维预测模型对深部体元的含矿性、品位和金属量进行预测。

(3) 安徽铜陵凤凰山铜矿和金川铜镍硫化物矿床三维可视化预测实例研究表明，矿体三维可视化预测方法适用于不同类型矿床的隐伏矿体三维定位定量预测，为深部找矿提供三维可视化定位定量指导。

陈建平，吕鹏，吴文，等，2007. 基于三维可视化技术的隐伏矿体预测[J]. 地学前缘，14(5):54-62.

蔺宏伟，王国瑾，2003. 三维带符号的欧氏距离变换及其应用[J]. 计算机学报，26(12):1645-1651.

刘亮明，舒志明，赵崇斌，等，2008. 矽卡岩矿床的汇流扩容空间控矿机制及其对深部找矿的意义：以铜陵—安庆地区为例[J]. 岩石学报，24(8):1848-1856.

毛先成，陈国珖，1988a. 香花岭锡矿田隐伏矿床的立体定量预测[J]. 桂林冶金地质学院学报，8(1):15-22.

毛先成,陈国珖,1988b. 香花岭锡矿床数学模型及立体定量预测初探[J]. 地质与勘探,24(10):25-31.

毛先成,2006. 三维数字矿床与隐伏矿体立体定量预测研究[D]. 长沙：中南大学.

毛先成,邹艳红,陈进,等,2010. 危机矿山深部、边部隐伏矿体的三维可视化预测：以安徽铜陵凤凰山矿田为例[J]. 地质通报,29(2/3):401-413.毛先成,唐艳华,邓浩,2012. 地质体的三维形态分析方法与应用[J]. 中南大学学报(自然科学版),43(2):588-595.彭省临,赖健清,毛先成,等,2012. 危机矿山深部隐伏矿大比例尺定位定量预测技术研究[M]. 北京:地质出版社.

瞿泓滢,裴荣富,王永磊,等,2010. 安徽铜陵凤凰山矽卡岩型铜矿床中辉钼矿Re-Os同位素年龄及其地质意义[J]. 岩石学报,26(3):785-796.

苏尚国,汤中立,周岱,2010. 金川含矿超镁铁岩侵入体侵位序列[J]. 地学前缘,17(2):118-126.

苏尚国,汤中立,罗照华,等,2014. 岩浆通道成矿系统[J]. 岩石学报,30(11):3120-3130.

汤中立,闫海卿,焦建刚,等,2007. 中国小岩体镍铜(铂族)矿床的区域成矿规律[J]. 地学前缘,14(5)：92-103.

田毓龙,包国忠,汤中立,等,2009. 金川铜镍硫化物矿床岩浆通道型矿体地质地球化学特征[J]. 地质学报, 83(10):1515-1525.

王世称,成秋明,范继璋,1989. 金矿综合信息找矿模型[J]. 吉林大学学报(地球科学版),19(3):311-316.

王世称,2000. 综合信息矿产预测理论与方法[M]. 北京：科学出版社.

肖克炎,朱裕生,宋国耀,2000. 矿产资源GIS定量评价[J]. 中国地质,27(7):29-32.

肖克炎,李楠,孙莉,等,2012. 基于三维信息技术大比例尺三维立体矿产预测方法及途径[J]. 地质学刊，36(3):229-236.

叶天竺,肖克炎,严光生,2007. 矿床模型综合地质信息预测技术研究[J]. 地学前缘,14(5):11-19.

袁峰,李晓晖,张明明,等,2014. 隐伏矿体三维综合信息成矿预测方法[J]. 地质学报,88(4):630-643.

赵鹏大,池顺都,1991. 初论地质异常[J]. 地球科学：中国地质大学学报,16(3):241-248.

赵鹏大,孟宪国,1993. 地质异常与矿产预测[J]. 地球科学:中国地质大学学报,18(1):39-47.

赵鹏大,胡旺亮,李紫金,1994. 矿床统计预测[M]. 北京：地质出版社.

赵鹏大,张寿庭,陈建平,2004. 危机矿山可接替资源预测评价若干问题探讨[J]. 成都理工大学学报(自然科学版),31(2):111-117.

曾认宇,赖建清,毛先成,2013a. 金川铜镍硫化物矿床岩浆通道系统的成矿模式[J]. 矿产与地质,27(4):276-282.

曾认宇,赖健清,毛先成,等,2013b. 金川铜镍矿床中断裂系统的形成演化及对矿体的控制[J]. 中国有色金属学报,23(9):2574-2583.

ALLAIS M, 1957. Method of appraising economic prospects of mining exploration over large territories: Algerian Sahara case study[J]. Management Science, 3(4): 285-347.

AGTERBERG F P, 1971. A probability index for detecting favourable geological environments[J]. Canadian Institute of Mining and Metallurgy, Special Volume 12: 82-91.

AGTERBERG F P, 1974. Geomathematics: Mathematical Background and Geo-science Applications[M]. Amsterdam: Elsevier Scientific Publishing Company.

AGTERBERG F P, BONHAM-CARTER G F, CHENG Q M, et al., 1993. Weights of evidence modeling and weighted logistic regression for mineral potential mapping[C]//DAVIS J C, HERZFECD U C. Computers in Geology: 25 Years of Progress. New York: Oxford University Press, 13-32.ASADI H H, HALE M, 2001. A predictive GIS model for mapping potential gold and base metal mineralization in Takab area, Iran[J]. Computers & Geosciences, 27(8): 901-912.BONHAM-CARTER G F, 1995. Geographic Information Systems for Geoscientists: Modeling with GIS: Computer Methods in the Geoscientists, Volume 13[M]. Oxford: Pergamon Press Ltd., 398.

CHEN L M, SONG X Y, KEAYS R R, et al., 2013. Segregation and Fractionation of Magmatic Ni-Cu-PGE Sulfides in the Western Jinchuan Intrusion, Northwestern China: Insights from Platinum Group Element Geochemistry[J]. Economic Geology, 108(8): 1793-1811.

HARRIS D P, 1969. Alaska′s base and precious metals resources: a probabilistic regional appraisal[J]. Quarterly of the Colorado School of Mines, 64(3): 295-327.

HOULDING S W, 1992. The application of new 3D computer modeling techniques to mining[C]//TURNER A K. Three-dimensional Modeling with Geoscientific Information Systems, NATO ASI Series 354. Dordrecht: Kluwer Academic Publishers, 303-325.

HOULDING S W, 1994. 3D Geoscience Modeling: Computer Techniques for Geological Characterization[M]. Berlin: Springer-Verlag.

HARRIS J R, WILKINSON L, GRUNSKY E C, 2000. Effective use and interpretation of lithogeochemical data in regional mineral exploration programs: application of geographic information systems (GIS) technology[J]. Ore Geology Reviews, 16(3/4): 107-143.

HARRIS J, SANBORN-BARRIE M, PANAGAPKO D A, et al., 2007. Gold prospectivity maps of the Red Lake greenstone belt: application of GIS technology[J]. Canadian Journal of Earth Sciences, 43(7): 865-893.

KEMP L D, BONHAM-CARTER G F, RAINES G L, et al., 2001[2016-06-18]. Arc-SDM: ArcView extension for spatial data modelling using weights of evidence, logistic regression, fuzzy logic and neural network analysis[CP/OL]. http://www.ige.unicamp.br/sdm. PORWAL A K, KREUZER O P, 2010. Introduction to the Special Issue: Mineral prospectivity analysis and quantitative resource estimation[J]. Ore Geology Reviews, 38(3): 121-127.SINCLAIR A J, WOODSWORTH G J, 1970. Multiple regression as a method of estimating exploration potential in an area near Terrace, B.C.[J]. Economic Geology, 65(8): 998-1003.

SINGER D A, 1993. Basic concepts in three-part quantitative assessments of undiscovered mineral resources[J]. Natural Resources Research, 2(2): 69-81.

ZHAO P D, 1992. Theories, principles, and methods for the statistical prediction of mineral deposits[J]. Mathematical Geology, 24(6): 589-595.

Three-dimensional visualization prediction method for concealed ore bodies in deep mining areas

MAO Xiancheng1,2, ZHANG Miaomiao1,2, DENG Hao1,2, ZOU Yanhong1,2, CHEN Jin1,2

(1. Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring, Ministry of Education, Changsha 410083, Hunan, China; 2. School of Geosciences and Info-Physics, Central South University, Changsha 410083, Hunan, China)

With the decreasing number of shallow deposits, exploration has gradually moved to deep mining areas. As a result, searching for a new deep metallogenic space is regarded as a new way to make breakthrough in ore prospecting. In order to solve the problem of locating concealed ore bodies, this work proposed a 3D visualization prediction method for concealed ore bodies based on previous research. The key of the method is ″location model-metallogenic information-3D prediction″. This conceptual model for ore body location realizes the transformation of metallogenic regularity to mineralization distribution regularity, and obtains the quantitative index of orebody space localization. We used morphological analysis, distance field or buffer analysis, alteration field analysis methods to analyze and quantitatively extract the metallogenic information index. Using nonlinear regression analysis and 3D fuzzy weights of evidence method, we established a 3D prediction model to predict the ore grade, metal quantity and ore-bearing property for the deep stereo-units. This work took the Fenghuangshan copper mine in Tongling of Anhui and Jinchuan Cu-Ni (PGE) sulfide deposit as examples to conduct 3D visualization prediction in deep mining areas. The results show that this method can be applied to the deep prospecting work of different types of ore deposits, and that the predicted results are true and reliable and have great significance for deep ore prospecting.

concealed ore body; conceptual model for location; metallogenic information; 3D visualization prediction; Tongling in Anhui; Jinchuan in Gansu

10.3969/j.issn.1674-3636.2016.03.363

2016-06-21；编辑：詹庚申

国家自然科学基金项目(41472301), 中南大学“创新驱动计划”项目(2015CX008), 新疆维吾尔自治区高层次人才工程项目

毛先成(1963—), 男, 教授, 博士, 主要从事隐伏矿三维预测与地学信息技术研究工作, E-mail: xcmao@126.com

P612

A

1674-3636(2016)03-0363-09