开口冷弯厚壁型钢轴压构件抗震性能研究
2016-11-07付小超李元齐沈祖炎
付小超,李元齐,沈祖炎
(同济大学 土木工程学院,上海 200092)
开口冷弯厚壁型钢轴压构件抗震性能研究
付小超,李元齐,沈祖炎
(同济大学 土木工程学院,上海 200092)
为研究开口冷弯厚壁型钢构件在轴向滞回荷载作用下的抗震性能,首先选取了3根壁厚t>6 mm的冷弯内卷边槽钢进行轴向滞回试验,然后建立相关的ANSYS有限元模型进行模拟计算,在与试验结果对比的基础上,选取了不同的腹板宽厚比(h/t=25~90)、绕弱轴长细比(λy=30~90)的构件进行参数化分析计算。研究结果表明:宽厚比、长细比是影响冷弯型钢抗震性能的两个主要因素,宽厚比(h/t)越大抗震性能越差,长细比(λy)越大抗震性能同样也越差,设计时应尽量避免选择长细比和宽厚比均较大的构件。
冷弯厚壁型钢;滞回;抗震性能;宽厚比;长细比
建筑业是冷弯型钢最主要的用户,国外发达国家建筑业用冷弯型钢已占其建筑用钢的40%~70%[1]。当前,关于冷弯型钢的研究侧重的是冷弯薄壁型钢(习惯上把壁厚不超过6 mm的冷弯型钢称为冷弯薄壁型钢[2]),并取得了非常丰富的研究成果,很多国家制定了相关设计规范及标准。然而,随着科技的发展,生产力水平的提高,冷弯厚壁(壁厚t>6 mm)型钢的生产及应用也慢慢开始广泛。目前,我国新的国家标准《冷弯型钢结构技术规范》修订工作正在进行,明确了新规范适用于0.6~25mm厚的冷弯型钢,并且确定需要增加冷弯型钢关于抗震性能的相关内容进入新规范。这些对冷弯厚壁型钢的研究都提出了新的要求和挑战。目前关于冷弯厚壁型钢的研究,主要停留在冷弯强化效应、残余应力分布及相应短柱轴压试验上[3-5],而冷弯厚壁类构件的抗震性能研究未见报道,只有少量关于薄壁型钢的抗震性能研究[6-9]。冷弯薄壁型钢抗震性能的研究主要是轴向滞回[6]、压弯滞回[7-8]和受弯构件滞回[9]的研究。由于研究对象均是薄壁型钢,宽厚比较大,容易发生局部屈曲甚至畸变屈曲[6],所以其表现出来的抗震性能不是很理想,研究结果表明:宽厚比、长细比、轴压比是影响其抗震性能的主要因素。然而,厚壁型钢力学性能与薄壁型钢存在诸多差异,关于其抗震性能的研究尚未见报道,因此本文选取了3根壁厚t>6 mm的冷弯内卷边槽钢(C形钢)进行轴向滞回试验,然后建立相关的ANSYS有限元模型进行计算,在与试验结果对比、验证模型准确性的基础上,选取不同宽厚比、长细比值进行参数化分析,以研究冷弯厚壁型钢的抗震性能。

表1 试件设计参数
1 试验概况
1.1试件选择
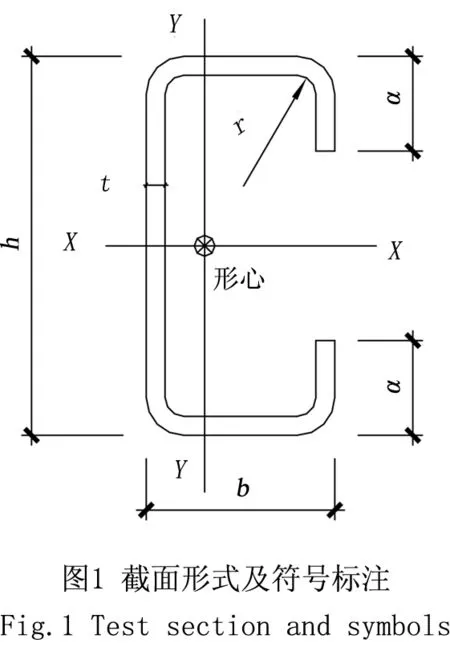
综合考虑现有试验设备加载能力、试验装置空间限制、试验成本等因素,本文选取了3根冷弯内卷边槽钢进行轴向滞回试验,其截面形式及符号标注如图1所示。
如表1所示,本试验选择表中3种规格的冷弯型钢进行试验研究,表中数据均为实测值。其中,λy为截面绕弱轴y的长细比,λym为实测母材屈服强度,其余符号意义见图1。
1.2试验装置
本试验在同济大学建筑工程系结构试验室进行,采用10 000 kN大型多功能静电液压伺服试验装置(MTS),竖向压10 000 kN、竖向拉3000 kN,有效行程±300 mm。上、下支座铰接是通过销铰支座连接实现;轴向反复拉、压荷载通过竖直千斤顶施加于试件截面的形心;加载时,水平千斤顶的水平位移保持不变,但其竖向位移跟动于竖向千斤顶,以模拟真实的铰接,并防止试件侧翻,保证安全。
1.3加载制度
[10]建议的加载制度,本试验以位移控制为主,通过控制作动器竖向位移进行加载,加载控制分弹性、屈服两个阶段。具体采用如下加载制度:
(1)屈服前分3级,每级为±0.25Δy、±0.5Δy、±0.75Δy,每级位移循环1圈;
(2)屈服后每级为±Δy、±1.5Δy、±2Δy、±3Δy……,每级位移循环3圈,直至试件破坏或严重变形,结束加载。
Δy为全截面屈服位移,见表1。
2 试验结果及分析
2.1试验现象
试验过程中,柱高中部变形最大,约加载到1Δy~1.5Δy时,柱中约1.5倍腹板高度范围内的板件开始出现表层氧化铁皮脱落现象,但各板件基本保持不变形,证明截面整体被压缩进入屈服,这不同于薄壁构件试验[6]的板件会在整体屈服之前局部屈曲、鼓曲,表面仍然光滑;查看此时的应变片读数,柱高中部应变基本进入了塑性应变。约加载至2Δy之后,卷边、腹板开始出现轻微变形,随着位移继续增加,其承载力开始下降,试件开始变形加剧,主要是整体弯向开口方向,卷边方向受压变形最厉害;到最终破坏时,卷边处的自由边凹进,翼缘略有外鼓,腹板由于受拉,未见明显鼓曲。由于试件均是厚壁型钢,宽厚比较小,不容易发生局部屈曲,所以试件在破坏过程中未见到明显局部屈曲现象。
2.2试验滞回曲线
将竖向往复荷载N和往复位移Δ记录的数据绘制成荷载-位移滞回曲线,见图2。由图可看出,

三者滞回曲线均比较饱满,荷载下降缓慢。对比文献[6]试验结果以及后文中有限元模拟的结果,发现冷弯厚壁型钢轴向滞回曲线要饱满的多,说明厚壁型钢滞回性能优越。
对比试件C4-t12-L30-T和C4-t12-L50-T,两者截面相同,只是长细比不同,长细比小的C4-t12-L30-T曲线饱满程度大于长细比大的C4-t12-L50-T,耗能更好;且峰值荷载之后,长细比小的每级滞回圈下降的也慢,延性更好。总之,相同截面,长细比小的抗震性能更好。此处试件C4-t12-L50-T的滞回曲线滞回圈数过少,显的不够饱满,主要原因是此试件是第一个做的试验,对试验机滞回加载掌控不足,导致其中有两级位移加载过头,超过控制位移。
对比试件C2-t8-L50-T和C4-t12-L50-T,两者截面不同,但长细比、宽厚比均相同,可是C2-t8-L50-T包络的面积远小于C4-t12-L50-T的,主要是后者管壁更厚,承载力更高,所以耗能能力更强。
3 有限元模拟
3.1模型的建立
本文采用ANSYS有限元软件进行参数化分析。选取SHELL181单元模拟槽钢构件。钢材选用Q235,屈服强度取名义屈服值fy=235mPa;选用双线性随动强化模型(BKIN),弹性模量E=2.06×105MPa,切线模量E1=0.001E;泊松比v=0.3。在构件模型两端添加端板和加劲肋,尽量模拟真实试验情况。采用自由网格划分,网格划分尺寸为6 mm×9 mm。
3.2模型准确性验证
有限元模型的正确性影响后续参数化分析的结果,是必要的前期工作,显得格外重要。先用本有限元模型对上文中3个试验构件进行模拟计算比较,发现无论是破坏模式还是滞回曲线,均与试验结果吻合较好,说明该模型建立的比较合理、准确,可以用于后续参数化分析。
另外,由有限元的von Misses应力分布图可看出,构件中部应力最大,达到了钢材屈服值fy=235mPa,证明构件全截面进入屈服状态,充分发挥了厚壁型钢材料的力学性能。
3.3参数化分析模型选择
在以上有限元计算模型准确基础上,此处选择2、4、8、12、16 mm的五种壁厚的冷弯型钢用于参数化分析,具体尺寸规格见表2。表中,L为试件长度;Δy(=Ny·L/EA)为全截面屈服位移;λy为截面绕弱轴y的长细比,其余符号见图1。
4 有限元结果分析
4.1滞回曲线
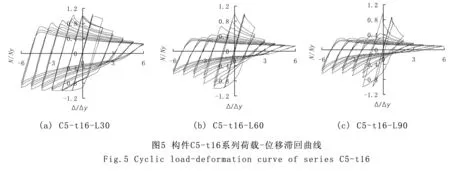
滞回曲线是分析试件抗震性能最主要的途径,从曲线中可以提取骨架曲线、刚度退化、耗能系数、延性系数等非常多的参数进行抗震性能分析。通过ANSYS有限元模拟所得典型滞回曲线如图3- 图5所示,其中第一象限为受压区,第三象限为受拉区。限于篇幅,此处只给出C1-t2、C3-t8、C5-t16三系列构件曲线图。
由图3-图5明显可看出滞回曲线是非对称的,是由于构件拉、压性能不一样,导致荷载不对等。还发现,宽厚比影响滞回曲线的饱满程度,如图3中,腹板宽厚比h/t=90,属于薄壁构件,发生了局部屈曲现象,受压区提前失稳破坏,较受拉区荷载值小的多;图5试件为小宽厚比(h/t=25),未发生局部屈曲,其滞回曲线比图3的要显得饱满多,抗震性能最优越;而宽厚比值相对居中的图4构件(h/t=37.5),滞回曲线饱满程度介于上述两者之间。长细比也是影响滞回曲线饱满程度的一个主要因素,同一截面构件,长细比越大,越容易发生整体失稳,其滞回曲线越不饱满,如构件C5-t16-L30与构件C5-t16-L90,虽然均未发生局部屈曲现象,但由于C5-t16-L90长细比较大,属于长柱,较长细比小的短柱仍显得不够饱满,抗震性能要差。

表2 模型规格尺寸


4.2骨架曲线
骨架曲线为滞回曲线,是各加载级第一循环的峰值点所连成的包络线。将所有表2中构件有限元模拟所得滞回曲线提取骨架曲线,结果如图6- 图7所示。为便于不同截面比较,图中骨架曲线坐标值均采用相对值,其中N、Ny分别为轴向荷载、全截面屈服荷载,Δ、Δy分别为轴向位移、屈服位移。
(1)长细比影响
图6为宽厚比相同,但长细比不同情况下的骨架曲线。从图6可看出长细比对构件抗震性能影响:相同截面不同长细比构件,其初始刚度相近;受压区(第一象限)峰值荷载长细比大的构件小于长细比小的构件,并且峰值点后曲线下降速度略快,说明长细比大的构件存在整体失稳现象;受拉区(第三象限)峰值荷载大小与长细比无关,但峰值点后长细比大者曲线下降速度略快,说明往复的构件失稳破坏造成了构件损伤累积,受拉后期承载力也随之降低。以上分析可看出,长细比对构件抗震性能影响较大,特别是对受压区峰值较大,对受拉区峰值点基本无影响,但无论受拉还是受压,长细比大者曲线下降均较快,延性降低,耗能能力减弱。
(2)宽厚比影响
图7为长细比相同,但腹板宽厚比不同情况下的骨架曲线。从图7可看出宽厚比对构件抗震性能影响:在相同长细比情况下,随着宽厚比增加,骨架曲线的峰值点逐渐降低,特别是大宽厚比的构件,如C1-t2-90,峰值达不到屈服荷载,说明出现了局部屈曲,构件提前进入屈曲,承载力较低;而小宽厚比的构件,如C5-t16-30,峰值略微超过屈服荷载Ny,说明无局部屈曲现象,截面能够进入塑性。
4.3刚度退化
刚度退化性能反应构件在地震荷载作用下后期抵抗变形的能力,本文采用同级变形下的环线刚度来描述试件的刚度退化,环线刚度的计算公式为:


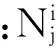
图8为长细比相同,但腹板宽厚比不同情况下的刚度退化曲线。由图8可看出,随着每级荷载位移的增加,切线刚度逐渐下降,其中前1~3级下降最快,之后趋于平缓,从图6-图8的滞回曲线上也可看出该下降趋势;λy=30构件的切线刚度大于λy=60、90的,说明长细比越大的构件越容易失稳破坏,构件刚度后期下降迅速,抵抗变形能力减弱;在相同长细比前提下,如构件C1-t2-L30与C5-t16-L30,宽厚比越大的构件,其切线刚度越小,说明冷弯薄壁型钢抵抗变形能力差,而厚壁型钢好,不容易变形。
5 结论
1)通过3根开口冷弯厚壁型钢的轴向滞回试验证明了该类试验的可行性,并且本文建立的有限元模型能较好模拟该类构件的滞回性能试验。
2)宽厚比、长细比是影响冷弯型钢抗震性能的两个主要因素,宽厚比越大越容易发生局部屈曲,抵抗变形能力减弱,滞回曲线不饱满,总体抗震性能越差;长细比越大越容易发生整体失稳,抗震性能同样越差;工程应用中,尽量避免选用宽厚比、长细比均较大的构件。
3)厚壁冷弯型钢总体抗震性能优越,全截面能进入屈服,滞回曲线饱满,强度下降缓慢,延性好,抵抗变形能力强,可以考虑推广到地震区使用。
参考文献:
[1]何保康,李 峰,丁国良.冷弯型钢在房屋建筑中的应用和发展[J].焊管, 2002, 25(5): 8-11.
[2]陈雪庭,张中权.冷弯薄壁型钢结构构件[M].北京:中国铁道出版社, 1990: 5-7.
[3]李黎明,姜忻良,陈志华,等.冷弯厚壁型钢钢管冷作硬化效应[J].天津大学学报, 2008, 41(1): 85-91.
[4]温东辉.冷弯厚壁钢管压弯构件抗震性能研究[D]. 上海: 同济大学, 2014.
[5]李元齐, 李功文, 沈祖炎,等.冷弯厚壁型钢考虑冷弯效应的屈服强度计算方法研究[J]. 建筑结构学报, 2015, 36(5):1-7.
[6]PADILLA-LLANO C D,MOEN M EATHERTON, et al. Compression-tension hysteretic response of cold-formed steel C-section framing members[C]//Proceedings of the 21st International Specialty Conference on Cold-Formed Steel Structures, 2012:118-137.
[7]董 军,陆 曦,王士奇.冷成型薄壁C型钢构件压弯滞回性能的数值分析[J].防灾减灾工程学报,2006,26(4): 419-424.
[8]杨 娜,彭 雄,杨庆山.冷弯薄壁型钢C型构件滞回性能[J].土木建筑与环境工程, 2012, 34(2): 69-76.
[9]谢兆平,宗周红,林 晓.冷弯薄壁型钢梁的滞回性能研究[J].河北工程大学学报:自然科学版,2009,26(3): 26-30.
[10]ECCS.Recommended testing procedure for assessing the behavior of structural steel elements under cyclic loads, 1st ed [S].Brussels, 1986.
(责任编辑李军)
Research on the seismic behaviors of opening cold-formed thick-walled steel under the axial cyclic loading
FU Xiaochao, LI Yuanqi, SHEN Zuyan
(Department of Structural Engineering, Tongji University, Shanghai, 200092)
In order to investigate the hysteretic behaviors of opening cold-formed thick-walled steel members under the axial cyclic loading, three cold-formed steel columns were tested. On the basis of compared with the test results, a finite element method (FEM) in ANSYS was established. The influence of width-thickness ratio (h/t) rang from 25to 90 for web and slenderness ratio about the weak axis y (λy) rang from 30 to 90 of such members were investigated by FEM. Analysis results indicated that the width-thickness ratio and the slenderness ratio about the weak axis y are the most important factors to affect the hysteretic behaviors. So, the cold-formed steels which with great width-thickness ratio (h/t) and great slenderness ratio (λy) should be avoided in designing, because they will lead to poor seismic performance.
cold-formed thick-walled steel; hysteretic; seismic performance; width-thickness ratio; slenderness ratio
2016-05-29
国家自然科学基金项目(51178330)
付小超(1983- ),男,江西樟树人,博士,主要从事钢结构、组合结构研究。
1673-9469(2016)03-0001-07
10.3969/j.issn.1673-9469.2016.03.001
TU392.1
A
