基于西洋跳棋的博弈程序研究
2016-11-05郑昌松贾丽娟权贺王彪
郑昌松+贾丽娟+权贺+王彪


摘要:为了提高计算机博弈水平,以西洋跳棋为研究对象设计博弈程序,采用Min-Max搜索算法实现对博弈树的搜索,根据α-β剪枝算法研究博弈树的估值深度,设计了搜索深度可以剪枝的博弈模型,该博弈模型解决了博弈程序布局方式、估值深度和搜索耗时等问题,提高了程序搜索效率和博弈性能,博弈程序在全国大学生博弈比赛中获得二等奖,在实际中得到了检验和应用,比赛结果表明了该博弈模型是可行和有效的。
关键词:计算机博弈;深度;搜索;布局;博弈树
DOI:10.15938/j.jhust.2016.03.005
中图分类号:TP311 文献标志码:A 文章编号:1007-2683(2016)03-0024-05
0引言
当前计算机博弈正越来越受到欢迎,它所具有的复杂性和挑战性吸引了许多学生和学者前去研究,西洋跳棋也称为国际跳棋,目前64格西洋跳棋已被研究完善,100格西洋跳棋其复杂性和难度都有所提升,布局和估值深度是当前主要的问题,搜索效率也是没有完全解决的难点,因此,人们更多地专注于100格西洋跳棋算法上的研究,100格西洋跳棋双方子力较多,布局变化万千,走法更是多种多样,本文致力于研究布局、估值和搜索,运用博弈树理论、极大一极小值搜索、虚拟静态估值等方法设计一种比较完善方案提高博弈水平,
1西洋跳棋的规则与棋盘
本文中提到的西洋跳棋是指100格西洋跳棋。
1.1基本规则
西洋跳棋规则相对比较复杂,棋盘是100格,上面有50个格可供棋子行走,如图1所示。对弈双方各有20颗普通棋子,当对方普通棋子走到自己方底线时就成为王子。在行棋过程中普通棋子只能向前走,当棋子具备连杀条件时必须连杀,当局面存在能吃掉对方棋子时必须吃子;王子可以向任意方向移动,比普通棋子更具有攻击力和防御力。当一方棋子被吃完或者没有可以移动的棋子时该方就输了。
1.2棋盘表示
西洋跳棋棋盘在程序中的常用表示方法有两种:一是二维数组表示棋盘,二是用比特棋盘。其中二维数组表示棋盘简单直观,易于访问,操作简单,比特棋盘访问效率高于数组棋盘,但是综合考虑各自优缺点后,本文选用10×10二维数组表示棋盘。
如图1所示,共有10×10个方格,故用10×10的(int型)二维数组表示,其中:0表示空白(无棋子),1表示黑棋,2表示黑王,-1表示白棋,-2表示白王,当普通棋子成王后,其棋子图形会由圆形变成正方形以区分普通棋子与王,即黑王用一个黑色正方形表示,白王用一个白色正方形表示。
2西洋跳棋的走法生成
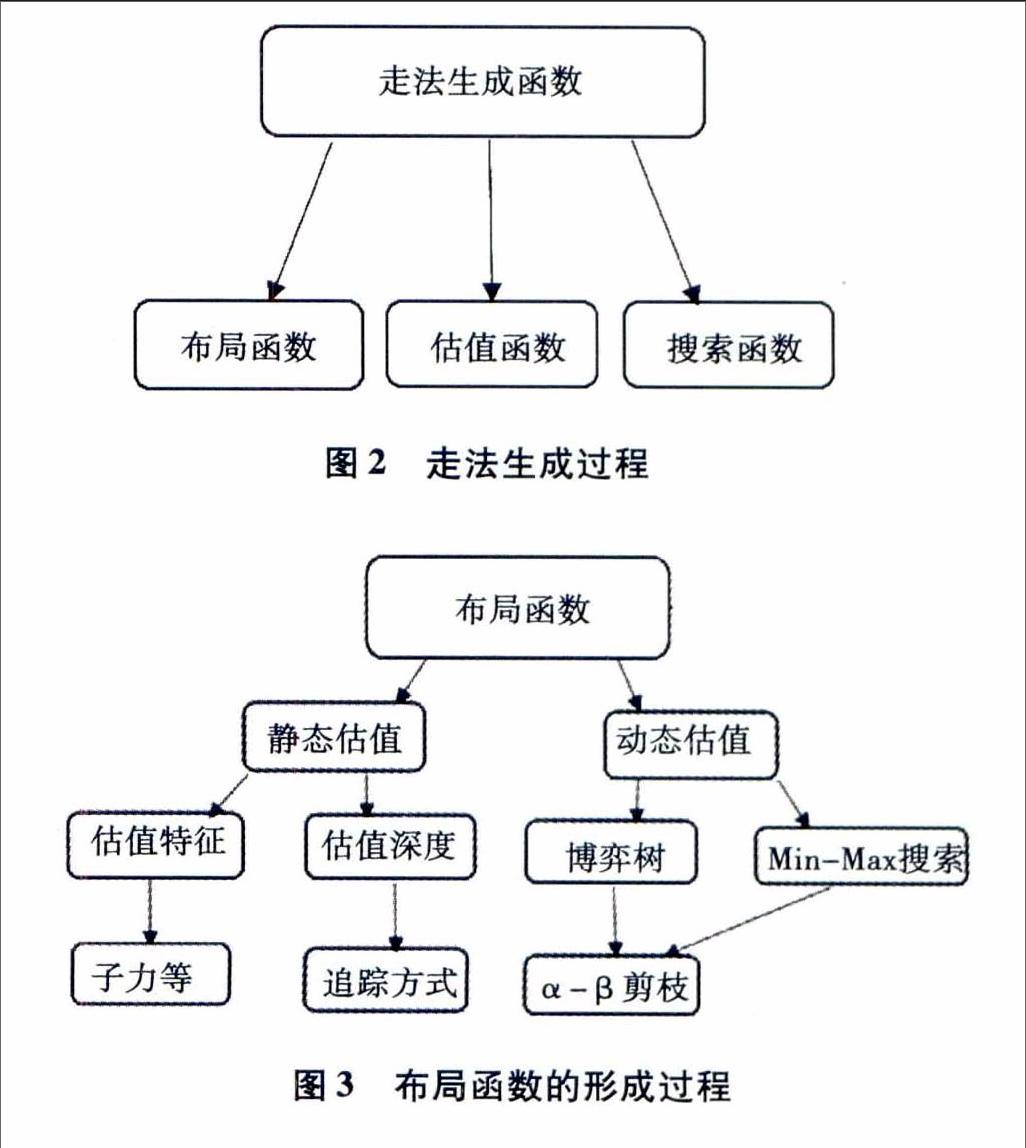
走法生成用专门的走法生成函数表示,生成函数包含西洋跳棋基本规则,行棋时必须严格遵循这些规则,它是程序正确博弈的保证。走法生成函数本身不产生任何行棋信息,它只负责按规则行棋。当布局函数、估值函数和搜索函数配合完成后会产生最优走法的相关信息,然后把这些函数传递给走法生成函数,最后由走法生成函数行棋,如图2所示。
2.1布局
布局是走法生成的关键部分,特别是开局决定着棋局后续发展的好坏。西洋跳棋棋子数量较多,布局时可以运用大量战术配合行棋规则,在博弈中往往可以反败为胜,使博弈时战斗激烈,精彩纷呈。布局既要考虑双方子力的差别,又要考虑当前这一步棋走完后对整个棋局的影响。布局可以采用虚拟走法,把每一颗能走棋子所有能走的方式都模拟走一遍,对走完后的局面做出评判,从所有能走方式中选取最优方式。布局时需要考虑的因素很多,要对局势整体把握,综合考虑,可运用的战术多种多样。例如布局可以利用能杀子时必须杀子规则来设置陷阱,牺牲一颗棋子换取对方多颗棋子,布局深度是决定棋局胜败的一个重要因素,行棋时要考虑棋局的未来发展。西洋跳棋是一种具有深度搜索的棋种,一步行棋往往能决定局势优劣甚至成败,估值深度可采用追踪方式,对能够移动的棋子各种行走轨迹追踪到底,分析该步行棋走后对后续局面造成什么影响。布局过程通过布局函数完成,完整的布局过程如图3所示。
3.2估值
在行棋过程中行棋者需要时刻掌握棋局的发展,掌握行棋方处于优势还是劣势,从而根据局势的优劣布局,估值可以分为静态估值和动态估值,估值方式采用估值函数评分,每个函数中有评分标准且相互之间不影响,分数可正可负可为零,棋子模拟行棋后调用估值函数评出相应的分数,估值时先把我方每一颗能走的棋子和能行走的方式都模拟走出来,再调用静态估值函数和动态估值函数给该模拟行棋估分并记录分数与行棋方式,找出所有方式中最高的分数,再比较所有能行走方式棋子中分数最高的棋子分数和行棋方式,最后生成相应的走法。估值过程如图4所示。
2.2.1静态估值
静态估值时要考虑行棋过程中的多种特性,但估值深度有限,需要动态估值共同配合完成整个估值过程。
1)静态估值。行棋过程中,特性考虑的越多越完善,估值就越好。经过反复研究,本文主要考虑几种典型的特性进行研究。例如棋子分布阵型、棋子数量、子力分布、王的数量等。单个估值函数有独立的评分公式,依据各自的性能评分。特性估值函数采用计算双方特性差的方式,如双方棋子数量差、具有攻击力棋子数量差等,以求获得比较完整的估值信息。例如子力估值函数评分公式可以采用式(1)~(4)。value_1、value_2、value_3代表子力估值函数中棋子数量、具有攻击力棋子数量以及具有防御力棋子数量所占的权重;Fen_value表示加权后算出的分值。根据局势发展,这些权重会根据棋子数量、位置等动态改变值的大小。因为棋子在棋盘不同位置,面临不同阵型等因素都会使其具有不同价值,我们在估值时必须时刻给其打分才能比较完善的评出有价值的分数,其它特性估值函数都是运用相同的原理。
2)静态估值深度。静态估值只考虑一步范围内的行棋估值,当行棋方模拟走出一步后就调用静态估值函数评出相应的分数。静态估值易于实现,考虑的范围广,当多个估值一起合作时会大大加强程序的博弈能力,但是静态估值毕竟没有深度,无法预测自己和对方行棋后对未来局面的影响。所以我们的估值必须要有深度。深度就是当我们行一步棋后模拟出对方和自己后面可以行棋的方式,当我们模拟完成后会评价该局面对我们是否有利,如果有利我们在实际行棋时就走这步棋,反之就放弃这步棋,寻找其它对我们有利的行棋方式。深度对博弈程序来说非常重要,深度决定了博弈程序的思考能力,当深度越深时程序看的就越远,可以看出对方行棋中的意图和陷阱并提前预防,这样在博弈过程中就可以占有利地位。结合动态估值就可以完成深度搜索。
2.2.2动态估值
动态估值涉及估值深度,可以通过具有一定搜索算法的博弈树完成深度搜索。
1)博弈树。博弈树是博弈程序设计中常用的一种行棋信息载体,它是行棋时生成的一棵可以完成记录行棋信息的树。在模拟行棋时模拟棋子所有可以行棋的方式并记录,树中每一个结点代表棋盘上的一个局面,对每一个局面(结点)根据不同的走法又产生不同的局面即生出新的结点,如此不断直到再无可选择的走法,即到达叶子结点(棋局结束),博弈树可以完整的记录行棋中的信息并将其保存到叶结点,再通过搜索算法进行访问。
2)动态估值。在博弈树中对每一层局面调用估值函数评分,找出每一层行棋中最好的行棋方式,记录每一层最高的分数走法生成,再求出每层的最优值。
因为西洋跳棋棋子数量较多,行棋时可以移动的棋子数量和方式也很多,所以涉及估值深度时要记录的信息量大,访问时耗费的时间也较多,利用博弈树可以很好的记录大量数据和快速访问,再结合合适的搜索算法能设计出很好的估值程序。
2.2.3估值评分
估值最后对所有静态估值函数和所有动态估值函数用统一公式评分,即:
可以看出每个权重大小是固定且相之间不同,这些权重系数需要经验获得,权重的不同说明每个特性估值函数的重要程度不同,模拟行棋后评出该步行棋的估值分数并记录。
估值可谓程序的大脑,在博弈过程中大多数的行棋都是估值决定的,所以估值的好坏直接决定着程序的博弈能力,在设计博弈程序的估值部分还可以加入许多其它算法以提高程序的博弈能力。
2.3搜索
搜索相当于程序的灵魂,在西洋跳棋博弈中搜索方式有很多,如Alpha-Beta搜索、Min-Max搜索、负极大值搜索、MTD(λ)搜索及PV搜索等,搜索深度越深,程序就看的越远,能力就越强。各种搜索方式都有各自的优缺点,经过精心考虑比较,本文采用Min-Max搜索,以博弈树为基础,结合Min-Max搜索方式设计程序的搜索。
2.3.1 Min-Max搜索
Min-Max搜索是一种比较基本的搜索方法,算法本质是白方总是试图寻找对自己最有利的行棋方式,而黑方总是寻找对白方最不利的行棋方式,如果将白方当作极大方,黑方就是极小方,结合博弈树Min-Max搜索过程如图5所示。
在博弈树搜索过程中,当白方搜索该层最大值后停止搜索,向下层搜索黑方最小值,当找到该层最小值时停止搜索,向下层搜索白方最大值,如此反复,直到遍历完整棵博弈树。
2.3.2α-β剪枝
生成博弈树过程中会生成许多叶结点,但是每一步行棋的时间是需要控制的,如果每一树枝都进行访问必然会耗费CPU大量时间,在博弈过程中如果行一步棋等很长时间是不允许的,所以访问博弈树时需要剪枝。剪枝的方式有很多,考虑到剪枝复杂程度和效率,确定采用α-β剪枝,该剪枝方法原理是设计一个评价函数,该函数可以对所有的棋局进行评估。当评价函数值大于0时,表示棋局对我方有利,对对方不利。当评价函数小于0时,表示棋局对我方不利,对对方有利,而评价函数值越大,表示对我方越有利。当评价函数值等于正无穷大时,表示我方必胜。评价函数值越小,表示对我方越不利。当评价函数值等于负无穷大时,表示对方必胜。假设博弈双方都是高手,在只看一步棋的情况下,我方一定走评价函数值最大的一步棋,而对方一定走评价函数值最小的一步棋。需要注意的是,在只看一步棋的情况下最好的行棋,从全局来说不一定就最好,还可能很不好,因此为了走出好棋,必须多看几步,从多种可能状态中选择一步好棋,这就需要有搜索深度,所以也需要剪枝。
α-β剪枝的关键是在生成博弈树和记录每层每个叶结点数据的时候记录每层最大值,当后面遍历博弈树时只要找到每层的最大值后就停止搜索,转向下一层搜索,这样在有的层次遍历中就不需要对所有的叶结点进行遍历,很大程度上节约了时间。如图5所示,在搜索到第3层时,如果之前生成博弈树时记录该层最大结点值是该层c2结点,那搜索到该结点时就停止搜索而转向下一层搜索,那c3结点及其以后的结点就不再进行搜索,该枝就相当于被剪掉,再比如搜索到第5层时,e9=9是这层最大值,生成博弈树记录第五层结点值中最大值是9,则当搜索到e9结点时就停止搜索,e9后面的树枝被剪掉,这样在我们对博弈树进行搜索时会节约很多时间,大大提高搜索效率,有利于提高博弈程序搜索深度。
当然还有很多剪枝算法,它们各具有其优势,运用多种算法的结合可以设计出更好的行棋方案。
3结论
基于本文研究的博弈模型所设计的西洋跳棋程序在2015年第四届中国大学生计算机博弈大赛中,经受住了考验,取得了国家二等奖的好成绩。该模型可以作为其它棋类博弈程序的研究基础。
博弈程序设计的3个重要过程是布局、估值和搜索,布局采用虚拟走法,从所有能走方式中选取最优方式,最优行棋方式是通过静态估值函数和动态估值函数记录每次模拟行棋分数和行棋方式,找出所有方式中最高的分数,再比较所有能行走方式中分数最高的棋子分数和行棋方式,最后生成相应的走法,这种把静态估值和动态估值相结合的方式,使程序在行棋过程中对局面有充分的掌控力。估值深度决定了博弈程序的思考能力,深度越深就会在博弈过程中占有更有利地位,动态估值时通过博弈树完整的记录行棋中的信息并将其保存到叶结点,再通过Min-Max搜索算法进行访问,生成博弈树过程中会生成许多叶结点,但是每一步行棋的时间是需要控制的,所以访问博弈树时需要剪枝,考虑到剪枝复杂程度和效率,采用α-β剪枝提高博弈程序在固定时间里的深度。
本文论述的估值方法可能不是非常完善,静态估值特性的种类考虑的有限,我们无法考虑到博弈中所有可能出现的局面,还有因为计算机执行速度问题,随着搜索深度不断增加搜索所花费的时间会越来越多。
在设计博弈程序时还可以加入其它高级算法,如神经网络算法、历史启发算法等。如果估值时能考虑更多的局面特性,用历史启发算法和α-β剪枝算法结合对博弈树进行剪枝,将会很大程度提高程序博弈水平,博弈往往和人工智能、机器学习密切相联,如果研究深入,完善程序设计,那么程序就具有了自我学习思考的能力和攻击实力,博弈是我们研究人工智能很好的一个平台,其易于实现、操作简单、成本低廉,涉及大量算法,可以将很多的想法通过博弈程序实现,为我们研究人工智能打下基础。
