数字带阻滤波器的设计及畸变矫正

及少勇+李龙谭+张洪飞+郭汉明

摘要：

在研究数字信号处理的过程中，可以采用数字带阻滤波器方法来进行消除交流电产生的工频干扰，但是传统的数字滤波器在起始位置存在畸变。利用双线性变换的方法将模拟带阻滤波器转换为数字带阻滤波器，借助离散时间系统中Z变换后的系统函数设计相应的数字带阻滤波器，以此来去除被测信号中的干扰信号，并通过两种简单算法来消除数字滤波器在起始位置的畸变。对一仿真混合正弦信号进行测试，试验表明，该滤波器可以很好地消除50 Hz 的工频干扰，且该方法具有设计简单、应用方便、实用性强等特点。

关键词：

带阻滤波器； 双线性变换； 畸变

中图分类号： TP 302.1文献标志码： Adoi： 10.3969/j.issn.1005-5630.2016.04.012

Abstract：

In the study of digital signal processing，digital band-stop filter approach is used to resolve power frequency interference which is from the alternating current.However，distortion is generated in the starting position with traditional digital filter.Using the system function in the Z-transform of discrete-time system，and converting analog-stop filter to bilinear digital-stop filter，we design an appropriate digital band-stop filter to remove the signal interference.It can eliminate the digital filter distortion of the starting position.Simulation results of a mixed sinusoidal signal show that the interference signal could be eliminated at 50 Hz frequency by the designed filter.The method has the advantages of simple design，convenient application，strong practicability and so on.

Keywords：

band-stop filter； bilinear transformation； distortion

引言

在信号采集中经常会采到带有工频干扰的信号，工频干扰是由交流供电的基频和各高次谐波导致的谐波干扰，会对激光共焦扫描显微镜等光学仪器设备的图像采集造成干扰，导致拍摄的图像分辨率下降。所以如何在保留有用信号的同时有效地消除这一干扰，对信号处理有着重要的实际意义[1]。

数字滤波的功能就是对输入序列通过一定的数字运算以实现滤除其中不需要的频率成分，而输出有用的序列[2]。数字滤波器包括有限冲激响应（FIR）滤波器和无限冲激响应（IIR）滤波器两大类型，在相同技术指标下，IIR滤波器比FIR滤波器需要的阶数低，而且还可以利用模拟滤波器的许多现成的设计公式、数据和表格，计算的工作量小，执行速度快，并且所用的存储单元少[3-4]。而在IIR滤波器的设计中，双线性变换法不仅能克服冲激响应不变法在设计高通带阻滤波器时出现频域混叠的缺点，而且易于设计。

然而，由于双线性变换是非线性变换，这种方法有其局限性：其一，会产生相移畸变，即滤波后的信号与原始信号之间存在相位差，这种畸变的矫正可以利用零相位矫正算法来消除[5]；其二，滤波后信号的起始位置会产生畸变，即在起始位置滤波效果不是很理想。本文主要介绍二阶IIR带阻滤波器的设计方法和对起始位置畸变的矫正方法。

数字滤波器的角频率为ω=2πfT，其中f为数字频域中的频率，T为采样周期。模拟频域中的角频率Ω与数字频域中的角频率ω的关系是非线性的，可以用公式表示[8]为

通过此式可以由要设计的数字滤波器的中心频率和带宽计算出模拟滤波器的Ω0和B值。

综合上述可知，滤波器的带宽决定了a的取值，滤波器阻带的中心频率决定了b的取值。因此，在设计数字带阻滤波器的时候可以先由带宽和中心频率计算出a和b，然后用式（3）设计相应的带阻滤波器。假设要滤除50 Hz的工频信号，采样频率为1 000 Hz，带宽为5 Hz，那么可以求出a=0.97，b=0.951，则系统函数为

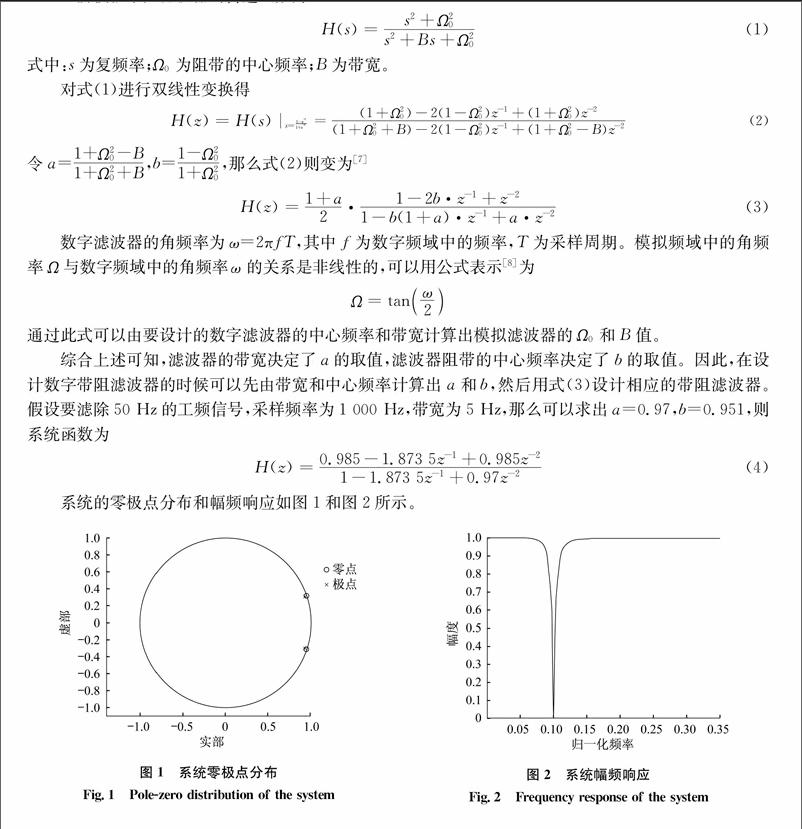
系统的零极点分布和幅频响应如图1和图2所示。

由图1可以看出，零点位于单位圆上，极点离零点很近，零极点的抵消作用明显。由图2频响特性曲线可以看出，滤波器的阻带较窄，过渡带较为陡峭，在归一化频率0.1处幅值为0，能对50 Hz的干扰信号很好滤除。

用x（n）表示信号的输入序列，y（n）表示信号的输出序列，则系统的差分方程为

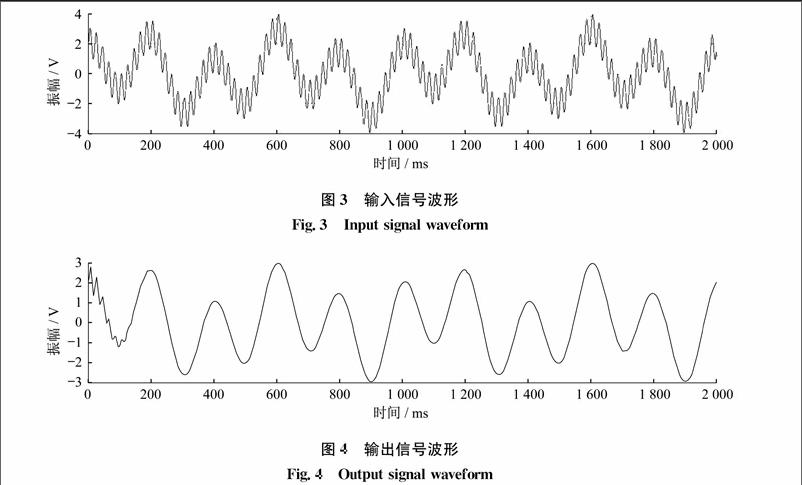
可以看到信号经过滤波后滤波效果相当明显，但是在起始位置滤波效果还很差，原因是在迭代过程中没有考虑滤波器的初始条件，刚开始点少，没能用到滤波器全部系数。当数据较短，而滤波器的阶数又比较高时，这种畸变会带来较大的负面影响。

为了克服滤波器的上述问题，本文提出两种方法来进行调整：一种是将信号进行延拓，在信号的起始位置前加上一段信号，经过滤波器后再将首部去掉；另一种是规定信号滤波后的初始化条件。设在这两种方法中，信号序列均为x（n），n=0，1，…，N，两种方法如下。

（1） 信号延拓的方法

首先，对信号序列x（n）的首部进行扩展，在x（n）前面添加K个数据，扩展后的序列记为x′n，n=0，1，…，N+K。

其次，进行滤波，将x′（n）通过式（5）滤波后的序列记为y′（n），n=0，1，…，N+K。

最后，删除y′（n）的扩展部分，将y′（n）的前K个数据删除，得到y（n）=y′（n+K），n=0，1，…，N。

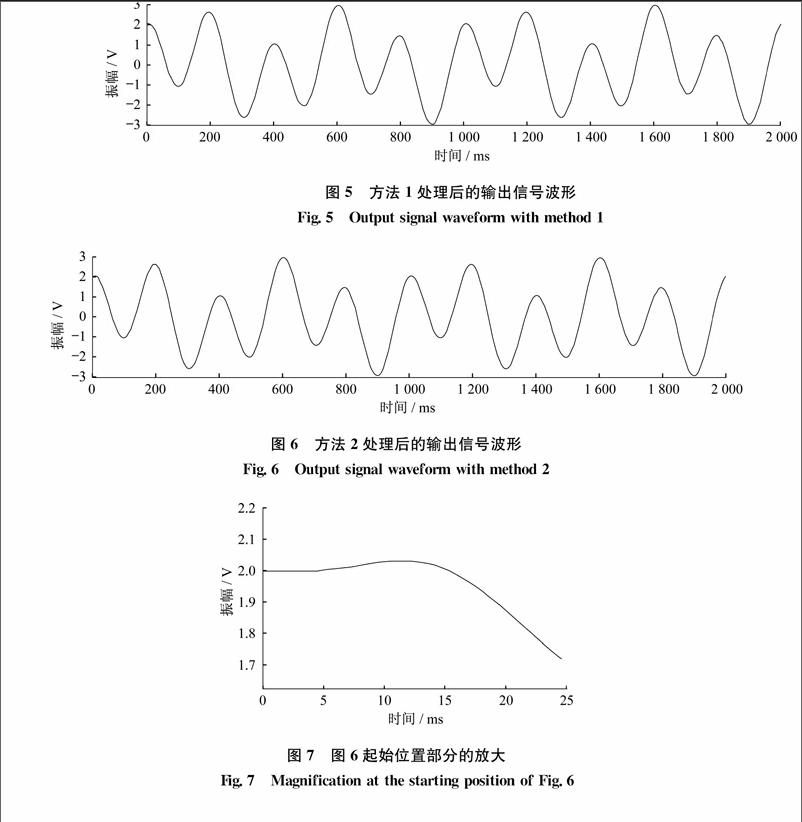
运用以上算法，假设K=200，再一次对式（6）信号进行滤波，得到滤波后的输出信号波形如图5所示。从图中可以看到处理后的信号达到了预期的要求，在起始位置处没有产生畸变。

（2） 规定信号滤波后的初始化条件

这种方法是将信号序列经过滤波器后的初始值进行定性规定，也就是在滤波的过程中，将滤波后的序列y（n）的前几个序列值进行定性规定。因为本文滤波器的系统函数是二阶数字滤波器，所以只需定性规定滤波后输出序列的第一个值y（0）和第二个值y（1）。让y（0）为一个噪声周期的平均值，使y（1）=y（0），那么初始化条件为

初始化后再从n=2开始进行式（5）的滤波，其中T′=采样频率/噪声频率，这里T′=20。

通过此种方法对式（6）信号进行滤波，输出后的信号波形如图6所示。图7是图6起始位置部分的放大。

从图6和图7可以看到处理后的信号同样达到了预期的要求，只是起始位置前几个点较为平滑，但并不影响滤波后的整体效果，这种影响可以忽略。

3结论

带阻滤波器在数字信号处理领域中有着广泛的应用，设计出可靠、频谱特性良好的带阻滤波器有着重要意义。本文提出了一种数字带阻滤波器的设计方法，即基于双线性变换的方法将模拟带阻滤波器转换为数字带阻滤波器。应用实例表明，这种方法设计的带阻滤波器会产生一定的畸变，通过文中给出的两种方法能够简单有效地消除这种畸变，并且由比较可知，方法2更为简单。

本文所设计的滤波器成功地滤去了信号的所有谐波干扰，完整地保留了有用信号，达到了设计要求。

参考文献：

[1]冯华君，洪淑月，施晓钟.借助Z变换和零极点设计数字陷波器[J].浙江师范大学学报，2004，27（1）：26-29.

[2]潘洪昌，张豪杰，张甫光，等.数字滤波在光学镀膜宽光谱监控中的应用[J].光学仪器，2006，28（4）：69-73.

[3]邢国泉.消除50 Hz工频干扰数字滤波器的设计[J].医疗卫生装备，2008，29（12）：25-27.

[4]张晓光，徐钊.IIR数字滤波器的优化设计和DSP实现[J].电子工程师，2006，32（3）：37-39.

[5]纪跃波，秦树人，汤宝平.零相位数字滤波器[J].重庆大学学报：自然科学版，2000，23（6）：4-7.

[6]钟洪声，崔红玲，皇晓辉.电子电路设计技术基础[M].成都：电子科技大学出版社，2012：259-261.

[7]张亚利，田社平.自适应跟踪数字带阻滤波器的设计及应用[J].中国计量学院学报，2003，14（3）：182-184.

[8]郑君里，应启珩，杨为理.信号与系统-下册[M].2版.北京：高等教育出版社，2000：216-218.