基于残差分析的MMC子模块故障定位
2016-11-04刘振兴
徐 恒,刘振兴
(武汉科技大学信息科学与工程学院,湖北武汉,430081)
基于残差分析的MMC子模块故障定位
徐 恒,刘振兴
(武汉科技大学信息科学与工程学院,湖北武汉,430081)
针对采用最近电平逼近调制(NLM)方式的模块化多电平换流器(MMC)系统,提出一种新的子模块故障定位方法。将给定的NLM阶梯波波形作为参考,与MMC输出的故障电压波形进行比较而构成残差,通过残差分析并结合子模块位置信息可以实现故障子模块的快速定位。在MATLAB/Simulink仿真平台中搭建了9电平MMC逆变器系统,仿真结果验证了该故障定位方法的有效性。
模块化多电平换流器;最近电平逼近调制;子模块;故障定位;残差分析
模块化多电平换流器(module multi-level converter,MMC)是柔性直流输电中高压交流传动系统电路的主要构成方式。相比于传统的2电平、3电平的电路拓扑结构,MMC因其可扩展性强、输出电平数高、功率因数高、输出电压谐波小等多项优势而具有很好的应用前景。
MMC由大量的子模块(sub-module,SM)所构成,因此对子模块故障定位的研究显得尤为重要。文献[1]对MMC子模块元件短路故障机理进行了分析,并通过增加器件的方法来对子模块进行保护,产生了一定的效果,但是该研究没有考虑所增加器件的失效问题;文献[2-5]提出了多种MMC子模块的故障诊断和保护方法,其基本原理都是对每一个子模块配备一个监控单元,这对于电平数不高的系统来说还是可行的,但是对于高电平、多子模块的MMC系统来说则极为不经济,因此需要探索其他更加经济而又快速、准确的子模块故障诊断方法。
本文针对采用最近电平逼近调制(nearest level modulation,NLM)策略[6]的MMC系统,提出一种基于残差分析的子模块故障定位方法。首先对每一相的各个子模块进行编号,然后将子模块故障状态下的系统输出波形与给定阶梯波的波形进行比较,根据两者之间的残差通过子模块故障定位器进行故障定位,从而可以通过控制单元来进行子模块的切除与替换。
1 MMC运行原理
对于一个N+1电平的MMC逆变系统,每一相都有上、下两个桥臂,每个桥臂都由一个限流电抗器与N个子模块串联而成。子模块的拓扑结构如图1所示。通过对子模块IGBT元器件的通断进行控制,实现如表1所示的子模块工作状态(其中0、1表示二极管和IGBT的关断和导通),从而达到输出电平数的叠加,最后得到理想的输出波形(一般为工频正弦波)。
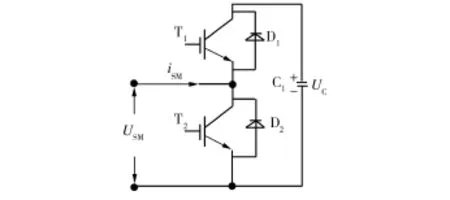
图1 MMC子模块的电路结构Fig.1 Circuit structure of MMC sub-module
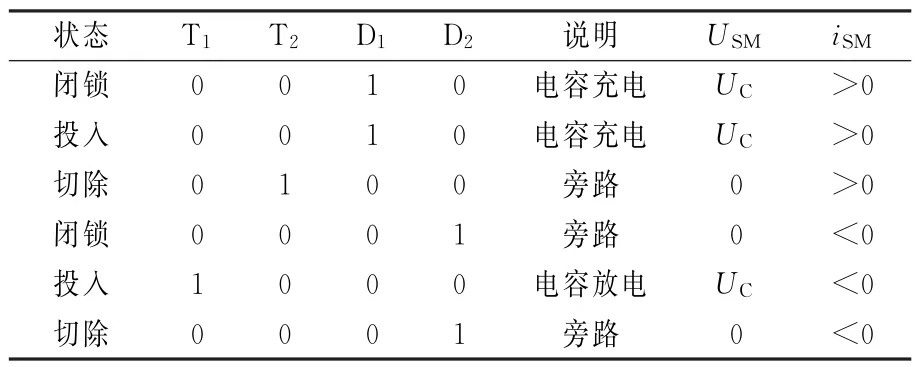
表1 MMC子模块的工作模式Table 1 Working modes of MMC sub-module
MMC正常工作必须满足两个条件:①维持直流电压,即三个相单元在任意时刻投入的子模块都相等;②任意时刻投入的子模块都为N个,即该相单元全部子模块的一半。此时MMC整流器输出达到额定电压Udc,输出的电平数为N+1。
2 最近电平逼近调制策略
2.1NLM的实现方法
NLM是一种重要的多电平阶梯波调制方式,其原理是使用最接近调制波的电压矢量或电平来瞬时逼近调制波(见图2),电平数越高,越近似于调制波。当电平数较多时,采用NLM具有非常大的优势。

图2 NLM原理Fig.2 Principle of NLM
用us表示调制波的瞬时值、UC表示子模块电容电压的平均值。一个桥臂含有的子模块数N一般是偶数。每个相单元在任意时刻只有N个子模块被投入。若这N个子模块在t=0时刻由上、下桥臂平均分担,则此时该相输出电压为0。根据图2,随着调制波由0逐渐升高,该相单元下桥臂投入的子模块数需要逐一增加,而上桥臂投入的子模块数要逐一减少,同时相当于输出一个高电平。此时该相单元的输出电压随着调制波的升高而增大,两者之差控制在±UC/2以内,可见UC是影响NLM逼近调制波的关键性参数。
在任意时刻,上桥臂和下桥臂需要投入的子模块数Nup和Ndown分别为:

式中:INT[us/UC]表示与us/UC最接近的整数。
2.2NLM的基波和谐波特性
以a相为例,设调制波ua(t)=umsinωt,由图2可知NLM的输出波形为1/4周期奇对称,运用傅里叶级数理论,根据前1/4周期内的一组开关角,就可以得到NLM的基波和谐波解析表达式:
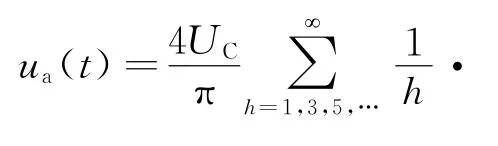
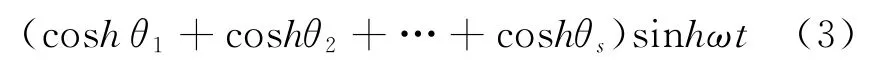
式中:θi(i=1,2,…,s)为第1个1/4周期内第i个电平阶跃的电角度;s为第1个1/4周期内的电平阶跃数,s=N/2。
使用反三角函数可以得到各个开关角的如下解析表达式,进而求得每个子模块的开关时间和电角度。

3 基于NLM的MMC子模块故障定位器
以a相为例,对a相各个子模块从上到下依次排序并进行编号,如图3所示。
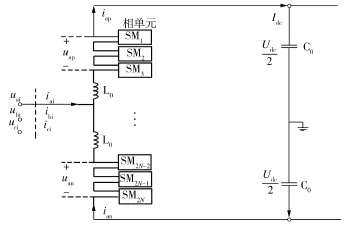
图3 子模块编号图Fig.3 Numbered sub-modules
由图2和图3可知,θ1对应于子模块3N/2+ 1,θ2对应于子模块3N/2+2,依此类推,最后θs对应于子模块2 N。由于NLM的输出波形为1/4周期奇对称,故可以得到下桥臂中子模块SM3N/2+1~SM2N的开通时长为:

因此,在一个周期内,下桥臂中子模块的开通电角度为:SM3N/2+1对应于θ1→(π-θ1),SM3N/2+2对应于θ2→(π-θ2),…,SM2N对应于θs→(π-θs)。由此可以得出下桥臂一个周期内子模块SM3N/2+1~SM2N的开关时间。
同理可推知,子模块SM1到SMN/2-1的开通电角度为:SM1对应于(π+2θs)→(2π-θs),SM2对应于(π+θs-1)→(2π-θs-1),…,SMN/2-1对应于(π+θ1)→(2π-θ1)。
确定好各个子模块的开关时间后,即可得到每个子模块的控制策略[7-8],此时可根据NLM策略和子模块编号方法对子模块故障定位器进行设计,如图4所示。其原理为:首先将根据NLM得到的输出波形作为参考电压,与MMC系统输出的故障电压进行差值比较,经过比例放大器进行归一化并求绝对值,得出一组幅值为1的开关脉冲信号;然后与该相所有子模块的开关信号组进行差值比较,同时经过绝对值计算和求最小冲量(在一段时间内的积分)计算,得到一个输出冲量最小值;最后与求最小冲量之前的各个值进行比较,若输出为0,则子模块存在故障,若输出不为0,则子模块无故障。
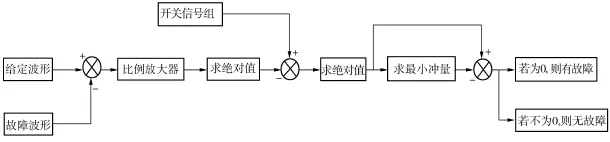
图4 子模块故障定位原理Fig.4 Principle of fault location for sub-module
4 仿真分析
在MATLAB/Simulink仿真平台中搭建基于NLM的9电平MMC逆变器系统,其中每个相单元由16个子模块构成,上下桥臂各有8个。直流侧额定电压Udc=32 k V,桥臂电抗器和输出滤波电抗器的电感值均为0.01 H,各个子模块电容电压参考值为4 k V,调制波幅值为15 k V,调制比m=0.9375,其三相输出电压波形如图5所示。

图5 基于NLM的MMC逆变器输出电压波形Fig.5 Output voltage waveforms of MMC inverter based on NLM
为了简化分析,将故障类型分为IGBT或续流二极管短路故障、IGBT或续流二极管开路故障以及子模块电容开路及短路故障[9-10],具体分类如下:
(1)T2或D2短路故障:导致子模块输出电压为0;
(2)T1或D1短路故障:导致短时间内电容迅速放电,同时子模块内会形成很大短路电流,若不加以抑制,会烧坏电力电子器件,其表现为子模块输出电压为0;
(3)T1开路故障:当iSM<0时,T1故障导致子模块输出电压为0;
(4)D1开路故障:子模块电容无法充电,同时该相电流断续,导致击穿子模块下桥臂电力电子器件,最后造成子模块输出电压为0;
(5)D2开路故障:当iSM<0时,导致子模块无法切除,T2两端会产生反向过压,进而击穿T2管,导致T2短路,最后使子模块输出电压为0。
(6)子模块电容开路故障:T2两端会产生过压,进而击穿续流二极管D2,导致子模块输出电压为0。
(7)子模块电容短路故障:同样会造成子模块输出电压为0。
以上故障最终都会导致子模块输出电压为0,因此进行故障仿真时,可将子模块输出电压设置为0。
以a相中的子模块7为例,设置该模块输出电压为0,得到故障波形与参考阶梯波形之差如图6所示。

图6 故障波形与参考阶梯波形之差Fig.6 Difference between fault waveform and referential step waveform
将差值通过比例放大器进行归一化处理,同时取绝对值,可以得到一组幅值为1的开关信号SQ。将SQ与a相各子模块的开通控制信号S1~S16进行求差比较,得到如图7所示结果。

图7 开关信号SQ与a相各子模块的触发信号求差后的波形Fig.7 Waveforms after differencing between trigger signals of sub-modules and switch signal SQ
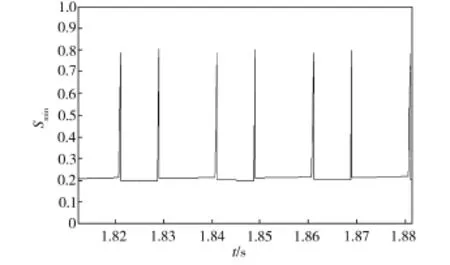
图8 冲量最小值Fig.8 Minimum value of the impulse
再将冲量最小值Smin与绝对值依次进行做差比较(见图9),若结果为0,则表示此模块存在故障;若比较结果不为0,则表示该模块无故障。由图9可知,子模块7的最后输出为0,因此可以定位该模块出现故障。同理,当其他子模块故障时也可得到类似结果。
综上所述,根据本文所提出的方法,可以比较快速有效地对采用最近电平逼近调制方式的MMC系统进行子模块故障定位,进而可以直接通过切除故障子模块并投入冗余子模块的方法来使系统在极短时间内恢复正常运行,保障了MMC系统的安全可靠性。

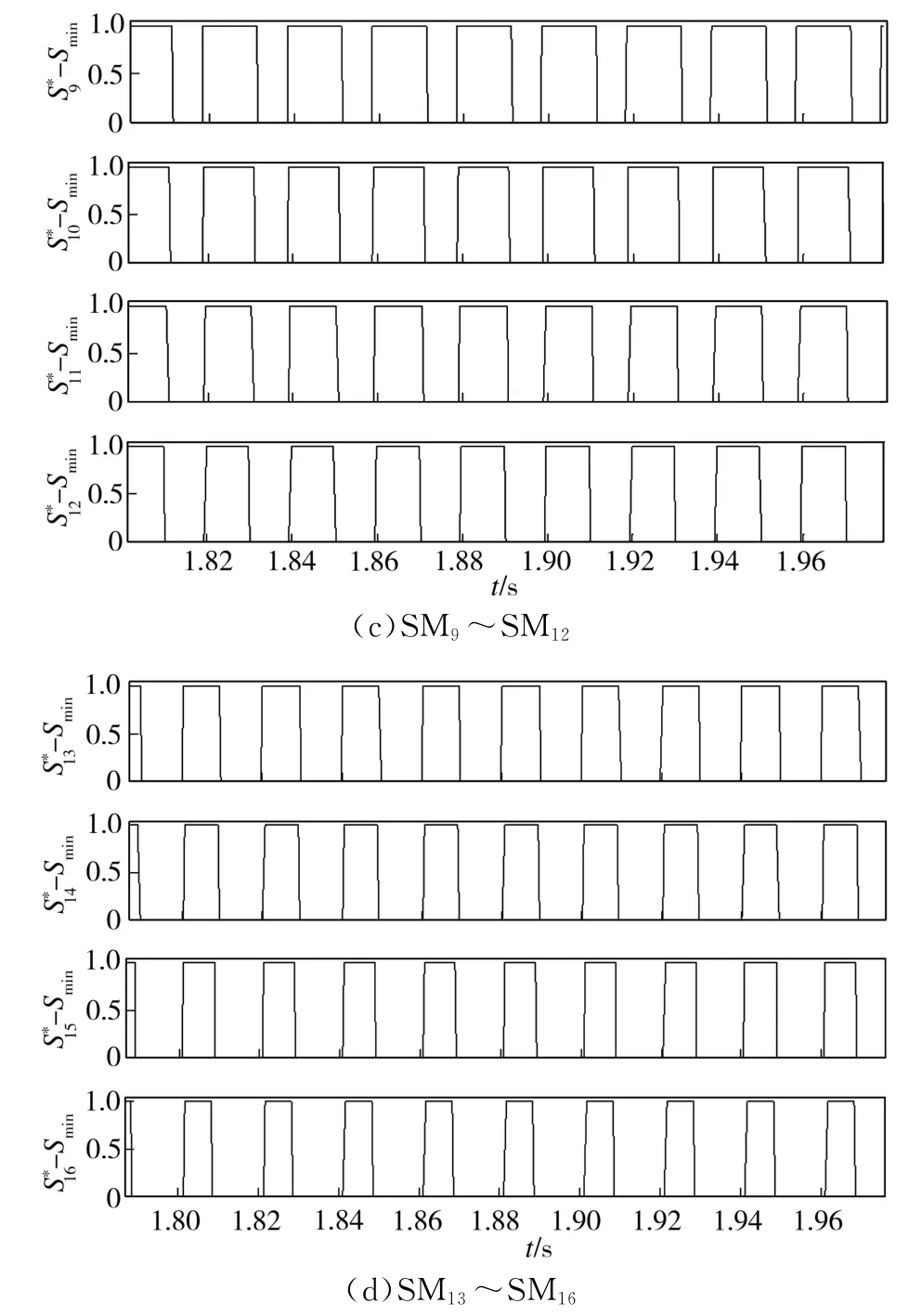
图9 ~与Smin的差值Fig.9 Difference between~and Smin
5 结语
本文以最近电平逼近调制策略为基础设计了模块化多电平换流器的子模块故障定位器,根据NLM的基本原理,通过比例放大器、做差比较等方法来进行子模块的常投入与常切除故障定位。仿真实验表明,本文提出的方法可以较好地进行子模块故障定位。进一步的研究可以根据本文思路,由单一子模块故障定位扩展到多子模块故障定位。
[1]敬华兵,年晓红,龚芬.MMC子模块元件短路故障机理及其新型保护策略[J].电工技术学报,2015,30(3):21-27.
[2]李探,赵成勇,李路遥,等.MMC-HVDC子模块故障诊断与就地保护策略[J].中国电机工程学报,2014,34(10):1641-1649.
[3]丁云芝,苏建徽,周建.基于钳位双子模块的MMC故障清除和重启能力分析[J].电力系统自动化,2014,38(1):97-103.
[4]管敏渊,徐政.模块化多电平换流器子模块故障特性和冗余保护[J].电力系统自动化,2011,35(16): 94-98.
[5]于泳,蒋生成,杨荣峰,等.变频器IGBT开路故障诊断方法[J].中国电机工程学报,2011,31(9):30-35.
[6]管敏渊,徐政,屠卿瑞,等.模块化多电平换流器型直流输电的调制策略[J].电力系统自动化,2010,34(2):48-52.
[7]管敏渊,徐政.模块化多电平换流器型直流输电的建模与控制[J].电力系统自动化,2010,34(19):64-68.
[8]Son G T,Lee H-J,Nam T S,et al.Design and control of a modular multilevel HVDC converter with redundant power modules for noninterruptible energy transfer[J].IEEE Transactions on Power Delivery,2012,27(3):1611-1619.
[9]安群涛,孙力,赵克,等.基于开关函数模型的逆变器开路故障诊断方法[J].中国电机工程学报,2010,30(6):1-6.
[10]周建.MMC-HVDC故障分析和保护策略研究[D].合肥:合肥工业大学,2013.
[责任编辑 尚 晶]
Fault location for sub-modules in modular multilevel converter based on residual analysis
Xu Heng,Liu Zhenxing
(College of Information Science and Engineering,Wuhan University of Science and Technology,Wuhan 430081,China)
This paper presents a new fault locating method for sub-modules in modular multilevel converter(MMC)using nearest level modulation(NLM)mode.The residual errors are achieved according to the comparison of the given NLM step waveforms and the faulty voltage waveforms outputted by MMC.The faulty sub-module can be quickly located through residual analysis and the position information of the sub-modules.A nine-level MMC inverter system is built by using MATLAB/Simulink software and the simulation results verify the effectiveness of the proposed method.
MMC;NLM;sub-module;fault location;residual analysis
TM72
A
1674-3644(2016)05-0371-05
2016-05-23
国家自然科学基金资助项目(61174107).
徐 恒(1986-),男,武汉科技大学硕士生.E-mail:15871354353@163.com
刘振兴(1965-),男,武汉科技大学教授,博士生导师.E-mail:zhenxingliu@wust.edu.cn
