基于改进灰关联度的雷达抗干扰能力评估算法

张亚楠

摘 要：将基于信息熵和灰色关联分析的评估算法引入到雷达抗干扰能力的评估中，分析了传统指标权重确定和灰色关联分析的局限性，将其信息熵结合起来考虑，可以在一定程度上解决这一问题。结合雷达抗干扰能力评估的特性建立了改进灰色关联度算法的模型，并利用实例验证了算法的相关内容。

关键词：雷达抗干扰；灰关联度；信息熵；指标权重

中图分类号：TN95 文献标识码：A DOI：10.15913/j.cnki.kjycx.2016.18.010

随着电子信息技术的不断发展，电磁环境变得密集复杂和交错多变。雷达担负着情报信息的保障支援重任，而且还面临着复杂电子环境下的对抗问题。要想深入分析、有效评估、充分发挥其抗干扰能力，目前还缺乏较为完整和成熟的评估算法。雷达抗干扰能力评估问题作为雷达抗干扰优化使用的重要环节，受到了国内外学者的高度关注。由于雷达抗干扰的过程是一个“不确定性”和“灰色性”的复杂过程，其中既有复杂的技术因素，又有大量不确定因素和灰色因素，所以，科学、合理地选择抗干扰能力评估算法成为了一个难题。目前，针对雷达抗干扰问题，多个国家和机构都进行了大量的研究。由文献[1]至文献[5]可知，目前的研究偏向于雷达抗干扰性能的定性分析，而针对雷达抗干扰能力评估算法的研究比较少；文献[6]至文献[8]中对评估算法的研究都存在一定的局限性，并且评估指标权重的确定主要是采用主观打分的方法，比如文献[9]中的层次分析法（Analytic Hierarchy Process，AHP），在客观性和可操作性等方面还需深入研究。为了解决AHP等方法主观性较强的问题，本文将文献[10]中的信息熵引入到评估算法的确定过程中，并借鉴文献 [11]中的灰关联度技术进行改进。将灰关联度技术与信息熵相结合，提出了一种雷达抗干扰能力评估新算法。通过一个应用示例对本文提出的评估算法进行了验证。

1 算法的基本原理

评估的主要目的是根据多个指标对备选雷达抗的干扰能力进行优劣比较的排序。为了方便对雷达抗干扰能力进行优劣比较和排序，各指标权重的确定需要考虑指标数据值的属性差异和相对重要性，因而需要寻求信息论的帮助，以便准确反映多个指标数据值组成不同备选雷达抗干扰能力的“不确定性”。文献[10]利用信息熵为解决该问题提供了很好的借鉴。为了解决评估中的灰色因素这一问题，灰关联度技术用最能反映各个不同雷达抗干扰能力的数据指标构成所对应的数据序列，用数据挖掘的方法揭示各个雷达抗干扰能力曲线的几何形状对应关系。几何形状差异越大，则灰关联度越小；反之，则越大。由于传统的灰关联度算法模型存在着不能客观反映各个指标“不确定性”差异的问题，所以，为了解决此问题，利用信息熵来确定这种差异，以此改进传统的灰关联度算法。

2 算法模型的建立

在进行抗干扰能力比较评估时，将参与评估的某一雷达作为抗干扰能力灰关联度比较这一命题的灰模式，将其设为 ， ，k为雷达的序数，m为所选雷达的数量；设 为抗干扰能力指标序列， ，i为指标的序数，n为所选指标的数量。根据图1可以将抗干扰能力灰关联度评估算法分为以下几个步骤。

2.1 建立评估指标体系

2.3 构造权重计算公式

各因素对雷达抗干扰能力影响程度的权重确定方法有很多，可采取以AHP为典型代表的主观定权方法，但是，这类方法往往会导致评估结果的主观偏差。信息熵能利用各指标信息的差异程度来计算各指标的权重，从而尽量消除人为干扰，使评估结果更符合实际情况。其构造权重公式的计算步骤如下。

2.3.1 确定新的标准化评估指标矩阵

2.4 确定雷达抗干扰能力评估比较的灰关联差异信息空间

在计算灰关联差异信息空间时，传统邓氏关联度计算方法并没有考虑到指标极性对计算结果的影响。利用2.3节第1步中计算得到的新评估指标矩阵作为灰关联度模型中的评估数据矩阵，从而实现其改进。因此，各个评估指标的标准序列值为1，雷达抗干扰能力评估比较的灰关联差异信息空间可以利用式（15）来确定：

2.5 确定单一指标的灰关联系数

根据灰关联度理论，将每一个灰关联差异信息空间中的模式和标准模式的几何形式相关度称为接近度，简称“灰关联度”。基于灰关联度可以进行模式分级，因此，可将灰关联度作为雷达抗干扰能力评估值。而本文中的灰关联度是由灰关联系数的加权和得到的。因此，需要确定指标的灰关联系数。设 和 在第i个评估指标上的灰关联系数记为 ，则其计算方法为：

3 应用示例

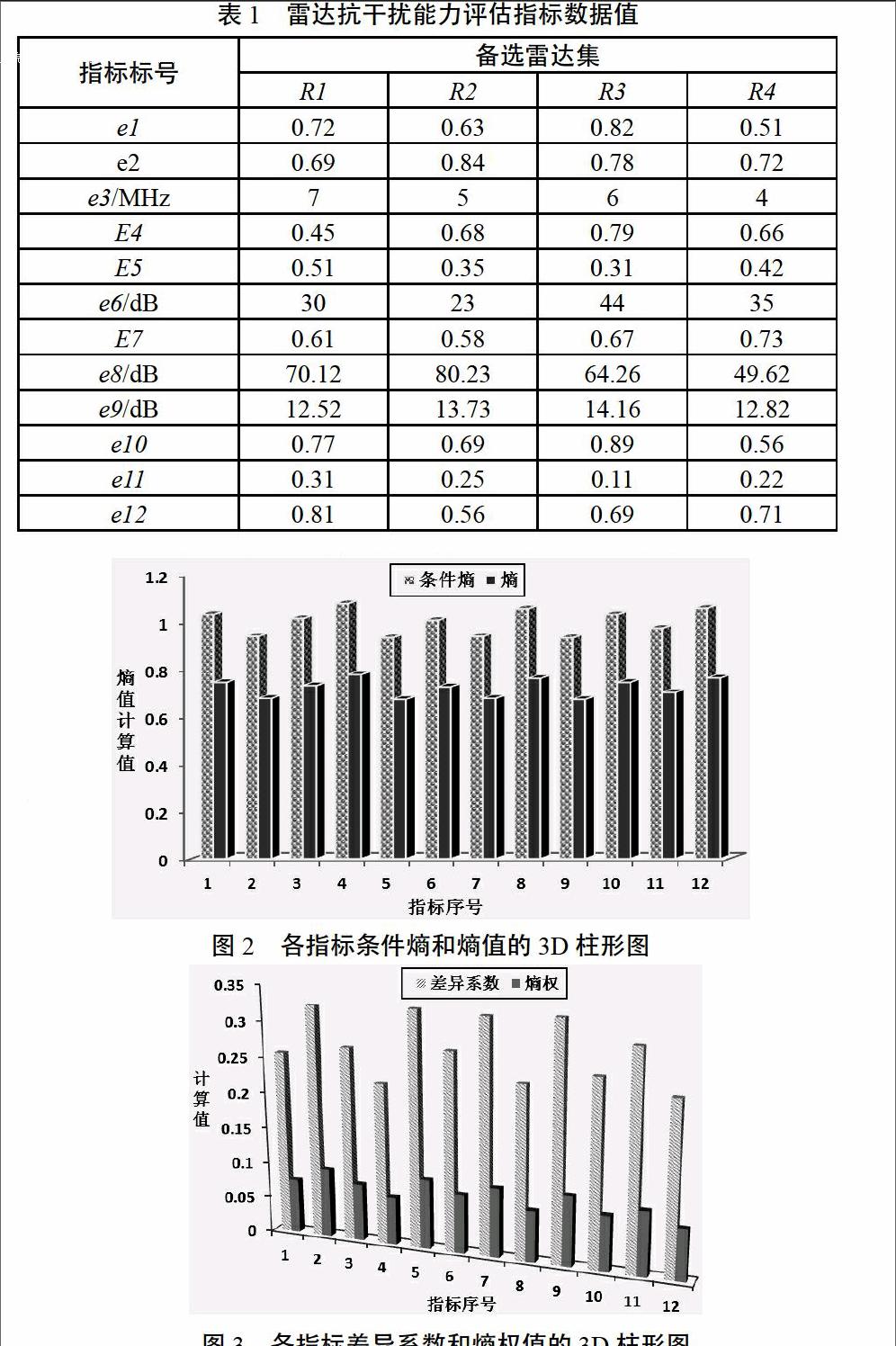
为了验证算法的有效性，现评估、比较4个不同雷达（即R1，R2，R3，R4）的抗干扰能力，以考核各雷达的抗干扰能力。结合实例和雷达抗干扰能力比较的评估指标体系，由专家定性分析打分得出雷达抗干扰能力优劣比较的各评估指标数据值如表1所示，再运用评估算法比较、评估4个不同雷达的抗干扰能力。

3.1 MATLAB仿真

由4个不同雷达R1、R2、R3和R4组成备选评估比较集，由12个评估因素组成某个雷达的抗干扰能力评估的指标集，通过表1的指标数据值，借助MATLAB软件仿真，可以仿真计算出各指标的条件熵和熵值结果，具体如图2所示。从图2中可以直观地反映指标的条件熵和熵值呈线性变化的特点。

再由2.3中的第5步和第6步计算出各指标的差异系数和熵权值，如图3所示。图3显示了各指标信息的差异程度，它决定了各指标的权重。根据计算结果，由各指标的权重可以判断各指标的重要程度。结合算例的指标权重分配结果符合客观实际。

3.2 模型的比对分析

利用传统灰关联模型计算本文实例的结果与本文评估模型的结果对比如图4所示。从图4中可以看出，采用本文算法可

以克服人主观因素而导致的偏差。本文评估模型对雷达抗干扰能力评估比较的排序结果与实际的排序结果是一致的，能较好地区分各备选雷达的抗干扰能力；而传统灰关联模型未考虑指标极性和指标重要性对评估结果的影响，容易有偏差。

4 结论

本文针对评估指标权重的主观误差，采用信息熵确定指标权重，提出了基于改进灰关联度的雷达抗干扰能力的评估算法，并通过实例仿真得出了计算结果。最后，进行了算法的比对分析，结合算例的仿真结果符合客观实际。这说明，该算法是有效和实用的，为解决雷达抗干扰能力评估问题提供了一种有效的方法和途径。

参考文献

[1]David A Shnidman.Radar Detection Probability and Their Calculation.IEEE Trans.on AES，1995，31（3）.

[2]SHEN Tong-yun，DING Jian-jiang，DING Yuan，et al.A Method of Detection Performance Modeling in Jamming Condition Based on Radar Network System.IEEE Trans.International Conference on Radar，2011.

[3]向龙，丁建江，吕金建.雷达组网系统抗复合干扰效果动态评估研究[J].现代雷达，2010，32（10）.

[4]陈永光，李修和，沈阳.组网雷达作战能力分析与评估[M].北京：国防工业出版社，2006.

[5]G.Richard Curry.Radar System Performance Modeling.2nd Edition.Boston|London：Artech House，2005.

[6]Geldermann J，Bertsch V，Treitz M，et al.Multi-criteria decision support and evaluation of strategies for nuclear remediation management.Omega，2009，37（1）.

[7]范俊方.组网雷达系统建模仿真与效能评估[D].西安：西安电子科技大学，2011.

[8]胡伟，柯韬，郭文立，等.老旧电梯风险评估方法研究[J].科技与创新，2016（3）.

[9]Saaty T.L..The Analytical Hierarchy Process.New York：MC-Graw-Hill，1980.

[10]杜言霞，林辉阳，汪月霞，等.符号动力学和信息熵在暴雨监测中的应用研究[J].科技与创新，2014（21）.

[11]S Liu，Y Lin.Grey Information： Theory and Practical Applications.London：Springer，2006.

〔编辑：白洁〕