自适应积分的递归实现研究

唐珺 杨道杰

摘要：文章首先介绍了分治算法与自适应积分的原理，然后用分治算法对自适应积分进行编程实现，最后将自适应积分在计算复杂度、误差等方面与组合辛普森积分公式进行了比较，分析了自适应积分的优越性。

关键词：自适应积分；组合辛普森积分；分治算法；复杂度；误差 文献标识码：A

中图分类号：O172 文章编号：1009-2374（2016）27-0013-04 DOI：10.13535/j.cnki.11-4406/n.2016.27.007

使用等距节点的组合积分公式，在整个积分区间使用相同的小步长h，以保证整体精度，但这并没有考虑曲线的某些部分剧烈变化的情况。而自适应积分能够根据函数的变化趋势自动选择合适的步长，本文在算法上以递归的方式对其进行了实现。

本文所用的递归算法属于分治算法：为了解决一个给定的问题，算法要一次或多次地递归调用其自身来解决相关的子问题。分治算法一般有着对数函数的复杂度，计算量较小，用在自适应积分上可用较少的计算量得到较高的精度，不失为一种好的算法，将在本文的开头进行介绍。

由于自适应积分的基础是辛普森积分，因此文中接下来会对辛普森积分公式进行简要介绍，最后再引入正题自适应积分。

1 分治算法简介

为了解决一个给定的问题，算法要一次或多次地调用其自身来解决自身相关的子问题，这些算法通常采用分治策略。将原问题分成n个规模较小而结构与原问题相似的子问题，递归地解决这些子问题，然后再合并其结果，就得到原问题的解。

分治算法在每一层递归上都有三个步骤：分解：将原问题分解成一系列子问题；解决：递归地解决各子问题，若子问题足够小，则直接求解；合并：将子问题的结果合并成原问题的解。

2 组合辛普森积分

2.1 辛普森公式

3.3 递归计算

接下来，从开始（其中是区间上数值积分的容差）将区间细分，在自区间上分别采用作为容差进行积分，利用式（7）测试精度，不断递归，直至满足精度要求。

4 算法实现

自适应积分在算法上基本上吻合上文提到的分治法的思想：分解：将原区间分解成两个子区间；解决：递归地算各区间的积分，并进行精度测试，如果满足要求就停止递归，否则继续；合并：将子区间的积分和

相加。

4.1 算法流程

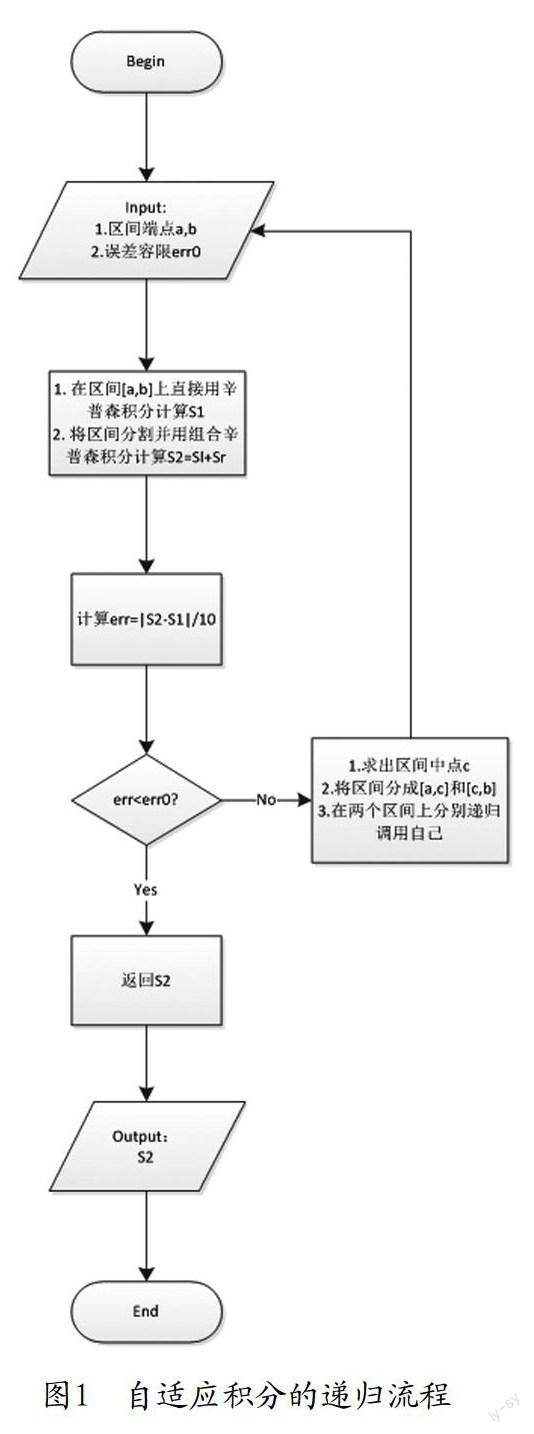
自适应积分具体的算法流程见图1所示：

4.2 核心代码

5 细节处理及改进

5.1 细节处理

5.1.1 自适应积分要求每次递归保存该区间直接积分以及子区间组合积分的和，甚至要保存误差，因此不能简单地用返回值来保存，要用变量的指针或者引用来保存。

5.1.2 本程序属于递归程序，一定要有终止条件，即上述程序的9～11行。

5.1.3 void函数虽然可以不用返回值，但在递归程序中，一旦计算精度符合要求，就要层层向上返回，否则程序会无穷递归，不断压栈，最终导致溢出。

5.1.4 计算子区间的积分时，别忘记将误差容限减半，保证子区间误差容限和等于原区间。

5.2 程序改进

上述程序仅仅能计算出最终的积分值，然而有时候需要保留最终的误差值和每一步的端点变化，这样能清晰地看出递归过程的区间细分的变化情况，因此上述程序可以做以下改进：

5.2.1 误差err的保存。误差的保存很简单，只需在函数的参数列表中传入误差的指针或引用即可，如float*err或者float&err。

5.2.2 端点值的保存。端点值要用数组来保存，且要有两个数组来保存，一个数组LeftPoints保存做端点值，另一个RightPoints保存右端点值。本文的编程采用C++程序，而C++标准库中有个可以很方便进行数组处理的容器，叫做vector，该容器定义了很多方便的操作，支持自动增长，并且安全性高，广为程序员所采用。因此本文也将采用vector来保存端点值，且用到容器上的两个操作：插入（任意位置插入insert和后插入push_back）和排序sort。

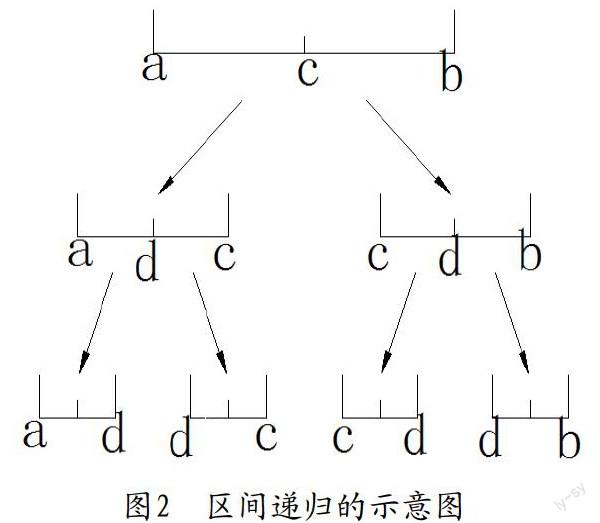
保存端点值时需要在程序特定地方加入push_back操作，具体放在哪里需要先分析程序的区间的递归过程，区间的递归示意图如下：

用数组LeftPoints存储区间左端点，根据上图，每层递归的左端点序列依次为{a}，{a，c}，{a，d，c，d}……根据大小进行插入添加端点的方法可以直接得到按照从小到大顺序排列的端点序列，但是操作上可能有一定的麻烦性，本文没有好的方法，可以留给读者讨论研究。本文采用先直接从数组后面添加（push_back操作），之后进行排序（sort操作）的方式得到最后的左端点序列，将push_back操作添加到上述代码的14与15行之间。而对于右端点序列的保存有个简单的办法，实际得到的端点序列有着以下的形式：

上面代码加黑的地方即是保存左端点序列的地方，不过程序最开始的时候需要先把端点a添加进去。

6 示例分析

用自适应积分求定积分的数值逼近，起始容差。真实值为-1.5487883725279481333……我们这里取11位精度-1.54878837253用于对比两种方法计算的结果。

6.1 自适应积分的计算结果

从图中可以看出，函数趋势变化较快的地方取点较密集，变化缓慢之处取点相对稀疏，具有自适应过程，而且在更少的计算次数下得到较高精度。本次计算的结果为-1.54878823413，误差为0.00000505957。而如果要达到11位精度（即计算结果为-1.54878837253），实际的计算次数为360次。

6.2 与辛普森计算结果的对比

如果单纯用辛普森积分的话，当划分区间数达到1300次左右才能使精度达到10-11，因此可以看出自适应积分可以大大减少计算次数，因为在曲线变化缓慢的地方划分的子区间更少，相对于完全等分区间来说，减少了不必要的计算量。

7 结语

本文所采用的分治算法是一种很重要的算法，有着完善的理论基础，在一些场合中非常实用，如一些需对原问题进行分割再综合的一类问题，实现方便，并且容易分析其复杂度。自适应积分公式有着极大的优越性，在工程或科学计算中应用广泛，本文通过分治算法对其进行了实现，效果良好，而且可以方便地通过设置误差容限来达到想要的精度。

我们在生活中要学会培养自己的算法素养，掌握一些基本的算法思想，如分治算法，并尝试将其用于一些实际问题中，如科学计算，提高分析并解决问题的能力。

参考文献

[1] John H.Mathews，Kurtis D.Fink.Numerical Method Using MATLAB[J].Fourth Edition，2014，（11）.

[2] Stanley B.Lippman，Josée Lajoie，Barbara E.Moo. C++ Primer[J]. Fourth Edition，2012，（2）.

[3] Thomas H.Cormen，Charles E.Leiserson，Ronald L.Riverst，Clifford Stein. Introduction to Algorithm [J].Second Edition，2001，（49）.

（责任编辑：黄银芳）