基于Monte Carlo法管道连接法兰泄漏概率计算

王程龙， 谢禹钧, 韦权权， 于小泽

(1.辽宁石油化工大学，辽宁 抚顺 113001； 2 中国寰球工程公司 辽宁分公司， 辽宁 沈阳 110000)



基于Monte Carlo法管道连接法兰泄漏概率计算

王程龙1， 谢禹钧1, 韦权权2， 于小泽1

(1.辽宁石油化工大学，辽宁 抚顺 113001； 2 中国寰球工程公司 辽宁分公司， 辽宁 沈阳 110000)

运用有限元软件Ansys对螺栓法兰接头进行模拟，得到了在预紧和操作工况下垫片的应力分布，计算出不同内压工况下垫片的应力。采用Monte Carlo法在管道工作压力不断波动时进行可靠性分析，创建极限方程并根据极限方程应用大型软件Matlab以变量的分布类型对变量进行反复随机抽样，计算出不同工作压力下螺栓法兰泄漏的概率。分析结果表明，工作压力的波动产生的附加载荷对螺栓法兰泄漏会产生很大的影响,必须加以足够的重视。

管道法兰;Ansys;附加载荷;Monte Carlo法;泄漏概率

油气管道是石油化工和能源企业的重要设施，螺栓法兰连接广泛应用于管道连接，除承受压力载荷外，通常还承受其他载荷，如风载荷、地震载荷、附加管道载荷。由于管道受力复杂，附加载荷对其紧密性有很大的影响，泄漏是螺栓法兰接头失效的主要原因[1]，笔者在前人的基础上[2]，运用有限元分析软件Ansys，考虑垫片的非线性和非保守性，分析了附加载荷对法兰接头紧密性的影响[3]，基于Monte Carlo概率分析的方法，以主要可能影响泄漏的因素为变量，计算出主要因素工作压力波动下螺栓法兰接头泄漏的概率，最终得到其可靠性评估，为石油、石化等企业诊断系统安全提供了一种有效的安全技术手段。

1　螺栓法兰有限元模拟

1.1法兰结构及参数

法兰选用ASME B16.5的NPS4，Class600的标准法兰，结构形式为带颈对焊法兰。法兰材料为15CrMo，屈服强度σy=280 MPa，室温下许用应力为[σ]f=178 MPa；螺栓公称直径为27 mm，数量为12个，材料为35CrMoA，屈服强度为440 MPa；垫片为柔性石墨缠绕垫，其载荷和变形呈非线性，尺寸Ф174.8 mm×Ф209.6 mm×4.5 mm。

1.2螺栓法兰连接的有限元模型

图1　螺栓法兰连接结构的有限元模型

与下法兰连接的筒体下表面为Y=0约束，上筒体端面自由。法兰、管道、垫片沿圆周方向0°和30°截面上施加对称约束，第一步加载螺栓预紧力F=26 235 N,其大小根据GB 150—2011《钢制压力容器》[5]计算(y取69 MPa)，施加在螺栓中截面上；第二载荷步锁住预紧位移；第三载荷步施加内压p=4.5 MPa，由内压引起的等效力20 MPa施加在上筒体端面。

1.3结果分析

图2为预紧时垫片的应力分布，图3为预紧+内压时垫片的应力分布。由图2、3可以看出，预紧工况和预紧+内压工况垫片应力沿圆周方向比较均匀,这两种工况沿径向的应力分布是由内向外逐渐增大的，最大应力出现在垫片的外边缘，这主要是因为法兰偏转引起的[6]。施加内压后垫片应力明显降低，由原来的29.45 MPa变成18.44 MPa，这主要是因为螺栓在内压工况下被拉伸导致的。升压后垫片应力明显降低，但是密封比压不低于pm=13.5 MPa[7]，因此不会发生泄漏。提取不同载荷步，得到不同压力下垫片外边缘的应力值SG。

图2　预紧时垫片应力云图

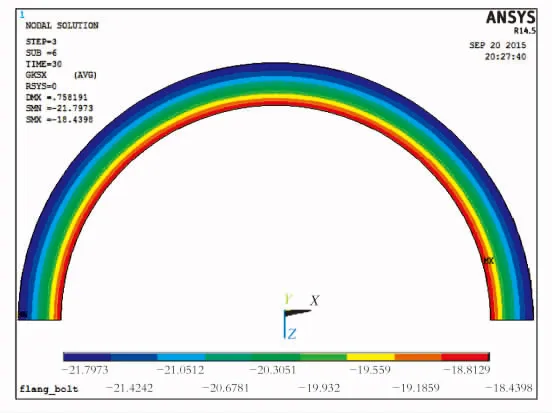
图3　预紧+内压时垫片应力云图

Fig.3Stress contour of the gasket in the pre pressing and internal pressure

1.4建立极限方程

使用Waters法对法兰结构进行分析[8]，垫片是螺栓法兰连接的核心，在法兰预紧和操作工况下，垫片外边缘最小压紧力SG必须达到密封比压pm，才能保证密封系统在规定泄漏率范围内，达到良好的密封效果，因此泄漏的极限方程为：

(1)

当y<0时，就代表法兰系统泄漏。

2　法兰接头失效概率的计算

2.1Monte Carlo方法

Monte Carlo法[9]是一种用数值模拟来解决与随机变量有关的实际工程问题的方法。对随机变量的数值模拟相当于一种“试验”，所以Monte Carlo方法又叫做统计试验法。它的基本原理是：由概率定义知，某事件的概率可以用大量试验中该事件发生的频率来估算，当样本容量足够大时，可以认为该事件发生频率即为概率。因此可以先对影响其可靠度的随机变量进行大量的随机抽样，然后把这些抽样值一组一组地代入功能函数，确定结构是否失效，最后从中求得结构的失效概率。蒙特卡罗法正是基于此思路分析的。设有统计独立的随机变量Xi(i=1,2,3，…，k)，其对应的概率密度函数分别为f(x1,x2,x3，…,xk),功能函数式为Z=g(x1,x2,x3,…,xk)。首先根据各随机变量的相应分布，产生N组随机数x1,x2,x3，…,xk值，计算功能函数值Zi=g(x1,x2,x3,…,xk)(i=1,2,…,N),若其中有L组随机数对应的功能函数值Zi≤0，则当N→∞时根据伯努利大数定理及正态随机变量的特性有:结构失效概率，可靠性指标。

2.2随机抽样理论

对垫片进行泄漏评定时，涉及到主要随机变量是垫片的残余应力SG和密封比压pm。大量的试验数据表明，垫片残余应力SG可用正态分布描述，在静载荷作用下应力的分布通常是正态分布，正态分布的概率密度为[10]：

(2)

其中，η1、η2均为[0,1]上均匀分布的随机变量，利用二元函数变换：

(3)

式中：ξ为标准正态分布N(0,1)随机变量抽样值。于是得到均值为μ，标注差为σ的随机变量抽样值为：

(4)

从而y就是需要的随机变量。

2.3Matlab计算法兰接头泄漏概率

对垫片外边缘应力SG和内压均值p进行试选，标准差取其均值的1/5，就有垫片残余应力和密封比压的分布参数[11]，可以开始对他们进行随机抽样。

用Matlab normrnd()函数对随机变量SG,pm进行N=106次随机抽样[12]，记数y<0的次数M，计算出M/N,就是螺栓法兰失效的概率。法兰泄漏率的计算流程如图4所示。对不同内压载荷工况下进行反复试算，将压力的均值μp在1.0～4.5 MPa分成30个区间进行随机抽样，最后得出随着不同内压的变化法兰系统泄漏的概率的变化曲线如图5所示。Matlab软件程序如下：

m = normrnd(MU,SIGMA,[1,106])

n = normrnd(MU,SIGMA,[1,106])

L=m-3*n

Q=length(find(L<0))

problity=Q/106

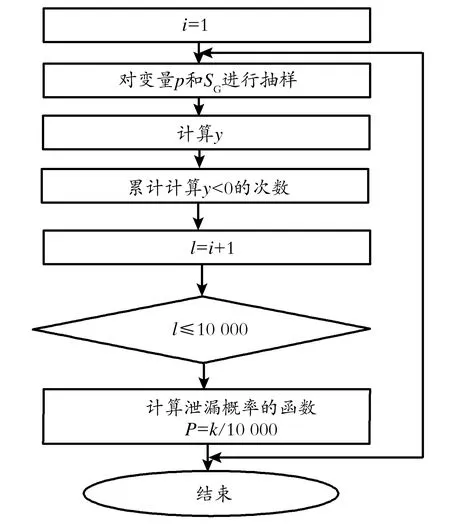
图4　法兰泄漏概率计算流程图

Fig.4Calculation flow chart of flange leakage probability

图5　法兰泄漏概率随内压变化

Fig.5The probability of flange leakage with internal pressure

3　结论

(1) 利用Ansys对管道螺栓法兰进行应力分析，在预紧工况和预紧+内压工况得出垫片的应力分布云图，预紧工况下垫片应力比加压后垫片应力要大，因为在内压作用下，螺栓发生拉伸变形，使垫片发生回弹导致的。

(2) 压力管道受内压、温度、自身约束影响会产生附加轴向力和附加弯矩[13]，这对法兰的紧密性有很大的影响，建立了附加载荷作用下垫片的紧密性极限方程。

(3) 把内压作为主要影响法兰泄漏因素[14]，由于管道中压力会不断地波动，压力产生的效应也有不确定性，所以把Monte Carlo法应用在螺栓法兰泄漏概率当中，应用Matlab对随机变量进行反复随机抽样，计算出管道法兰泄漏的概率。为评估压力管道安全提供一种有效的方法。

(4) 绘制不同压力作用下，螺栓法兰泄漏的概率曲线，随着内压升高，泄漏的概率也会越大，与现场实际情况也相吻合，因此在压力管道中内压产生的附加载荷对泄漏的影响不容忽视。

[1]Koves W J. Analysis of flange joints under external loads[J]. Journal of Pressure Vessel Technology, 1996, 118(1): 59-63.

[2]Abid M. Determination of safe operating conditions for gasketed flange joint under combined internal pressure and temperature: A finite element approach[J]. International Journal of Pressure Vessels and Piping, 2006, 83(6): 433-441.

[3]孙世锋, 蔡仁良. 承受外弯矩作用的法兰接头有限元分析[J]. 压力容器, 2003, 20:19-22.

Sun Shifeng,Cai Renliang.Finite element analysis on the bolted flanged joint subjected to external bending moments[J].Pressure Vessels,2003,20:19-22.

[4]余伟炜，高炳军.ANSYS在机械与化工装备中的应用[M].北京：中国水利水电出版社，2007:156-169.

[5]全国锅炉压力容器标准化技术委员会.GB 150—2011《压力容器》[S].北京：中国标准出版社，2011.

[6]喻健良, 张忠华, 闫兴清,等. 高温下螺栓-法兰-垫片系统密封性能研究[J]. 压力容器, 2012, 29(5):5-9.

Yu Jianliang,Zhang Zhonghua Yan Xingqing,et al.Seaing performance of bolted flange joints at high temperature[J]. Pressure Vessels, 2012, 29(5):5-9.

[7]Boqin G, Ye C, Dasheng Z. Prediction of leakage rates through sealing connections with nonmetallic gaskets[J]. Chinese Journal of Chemical Engineering, 2007, 15(6): 837-841.

[8]蔡仁良，顾伯勤，宋鹏云.过程装备密封技术[M].北京：化学工业出版社，2002:51.

[9]戴树和，王明娥.可靠性工程及其在化工设备中的应用[M].北京：化学工业工业出版社，1987.

[10]王侨, 谢禹钧, 龚雪. 基于蒙特卡罗法管道失效概率的计算[J]. 辽宁石油化工大学学报, 2012,32(2):67-69.

Wang Qiao,Xie Yujun,Gong Xue.Calculation of pipe failure probability based on monte carlo method[J]. Journal of Liaoning Shihua University, 2012,32(2):67-69.

[11]蔡永梅, 张瑞革, 谢禹钧. 非标准法兰的有限元分析及可靠性设计[J]. 石油化工设备, 2008, 37(2)：32-35.

Cai Yongmei,Zhang Ruige,Xie Yujun.Finite analysis of nonstandard flanges[J].Perto-Chemical Equipment, 2008, 37(2)：32-35.

[12]Bouzid A, Chaaban A. An accurate method of evaluating relaxation in bolted flanged connections[J]. Journal of Pressure Vessel Technology, 1997, 119(1): 10-17.

[13]Liu R, Gu B, Chen Y. Analyses of the strength and tightness of the bolted flanged connection under the action of additional loads[J]. Chemical Engineering and Machinery, 2007, 34(5): 264-268.

[14]陈永林, 顾伯勤. 垫片密封的可靠性分析方法[J]. 润滑与密封, 2001(2):24-25.

Chen Yonglin,Gu Boqin.Reliability analysis method of gasket sealing[J].Lubrication Engineering，2001(2):24-25.

(编辑王亚新)

Calculation of Leakage Probability of Pipe Connecting Flange Based on Monte Carlo Method

Wang Chenglong1, Xie Yujun1, Wei Quanquan2, Yu Xiaoze1

(1.LiaoningShihuaUniversity,FushunLiaoning113001,China;2.LiaoningCompanyHQCEC,ShenyangLiaoning110000,China)

Bolted flange joints were simulated with the finite element software Ansys, getting the gasket stress distribution under the condition of the preload and operation, and calculating the gasket stress under different working condition of internal pressure. Due to constant fluctuations in pipeline pressure and the pipe stress complex, the working pressure, temperature, uncertain factors such as their own constraints on its tightness should be fully considered. The Monte Carlo method is used to have reliability analysis in pipeline working pressure fluctuating. Limit equation is created and according to the distribution of the variable type and limit equation using large-scale software Matlab is used to repeat random sampling to calculate the probability of bolt flange leakages under different working pressures. The results show that, the additional load produced by working pressure fluctuation will have a very big effect on the bolt flange leak, that must be got seriously enough attention.

Pipe flange; Ansys; Additional load; Monte Carlo method; Leakage probability

1006-396X(2016)02-0095-04

投稿网址：http://journal.lnpu.edu.cn

2015-10-09

2016-01-12

辽宁省教育厅重点实验室项目(LS2010100)。

王程龙(1989-)，男，硕士研究生，从事流体密封技术研究；E-mail：wangcl0418@126.com。

谢禹钧(1960-)，男，博士，教授，博士生导师，从事力学、机械流体密封方面研究；E-mail：yjxie@lnpu.edu.cn。

TE311

Adoi:10.3969/j.issn.1006-396X.2016.02.018