移动线载荷板局部非线性响应的网格重划分数值方法

李元泰，赵耀，袁华，王波

1华中科技大学船舶与海洋工程学院，湖北武汉430074

2武昌船舶重工集团有限公司，湖北武汉430064

移动线载荷板局部非线性响应的网格重划分数值方法

李元泰1，赵耀1，袁华1，王波2

1华中科技大学船舶与海洋工程学院，湖北武汉430074

2武昌船舶重工集团有限公司，湖北武汉430064

在船舶建造中，常涉及板的焊接、线加热、局部滚压成型等加工方式。该加工方式中的载荷作用区域相对于板的尺度较窄且具有高度的非线性特征，同时载荷稳定移动。把握加工参数与响应的关系在加工过程中很重要。由于载荷移动导致板局部非线性响应的特性不断随之变化，故其相应的计算非常复杂。常规的数值方法是主要采用的手段，但由于该方法在载荷全局作用区域上需预先将网格细密划分，导致计算效率低下。如果考虑到在该加工方式中载荷作用区域之外的大部分区域处于弱非线性或线弹性状态，在数值模拟中将载荷当前作用区域的单元划分细密，远离载荷作用区域划分得相对较粗疏，同时载荷移动时细密网格随着载荷一起移动，即采用网格重划分数值方法来分析上述问题就能节省大量计算时间。针对该方法，重点探究细密网格尺寸以及网格重划分频度对数值计算的影响及其与计算效率和精度的关系，并以板局部滚压成型加工为例进行数值计算。结果表明，该方法可作为移动载荷作用下板局部非线性响应的一种高效的计算手段。

移动线载荷；网格重划分频度；细密网格尺寸

网络出版地址：http://www.cnki.net/kcms/detail/42.1755.TJ.20160921.1339.022.html期刊网址：www.ship-research.com

引用格式：李元泰，赵耀，袁华，等.移动线载荷板局部非线性响应的网格重划分数值方法［J］.中国舰船研究，2016，11（5）：63-70.

LI Yuantai，ZHAO Yao，YUAN Hua，et al.Rezoning method in nonlinear simulation of plate under moving load［J］. Chinese Journal of Ship Research，2016，11（5）：63-70.

0　引言

在船舶金属板结构的加工成型过程中，常伴随着载荷作用区域相对于被加工板面尺度较窄的移动线载荷作用（如热载荷、力载荷等），如金属板的焊接和线加热成型；通过一对上下的凹凸滚轮加压滚动，对放置于凹凸滚轮之间的板曲面成型的过程。这类加工的特点是，在载荷作用区域内，不论是热载荷还是力载荷，其载荷量均非常大，且作用过程稳定移动。从而在载荷作用的狭窄区域附近，被加工板壳产生较大的塑性变形，局部响应呈强非线性特征，而在远离这一区域的大部分被加工板壳则处于弱非线性或线弹性状态，同时随着载荷的移动，被加工板经历着加载、卸载的变化。

实际情况中，由于载荷大小及路线的变化，加工精度和效率与加工参数之间存在着复杂的对应关系，因此高效率和高精度地计算预报不同加工参数与加工要求如变形量之间的关系是非常必要的。对于这样一个涉及弹塑性同时包括载荷移动甚至接触变化的复杂问题，使用完全的理论求解分析几乎是不可能的，目前一般会借助于非线性有限元方法来解决。

常规的弹塑性数值方法对于处理这样一类问题通常依据经验在非线性特征明显的载荷区域周围划分十分细密的网格，以保证计算结果的准确性。这样导致在移动载荷尚未作用前和已经作用后的整个载荷移动线路上均需要预先划分为细密单元，使得网格数量过于庞大，导致非线性迭代计算十分耗时，往往模拟一次简单的载荷计算过程需要很长时间，计算效率非常低下。因此，针对该问题的高效弹塑性计算数值方法研究就显得尤为重要。如果能够仅仅在载荷作用区域范围内加密计算网格尺度，而在其他地方适当粗化计算网格尺度，减少节点数，缩小刚度矩阵规模，计算效率就会提高。网格重划分数值方法可以有效解决该类问题。其主要做法是根据分析过程中载荷当前的位置和移动路线，在载荷作用的一段区域内将网格进行细密划分，而对其他区域则适当将网格粗疏划分；而且在细密网格随着载荷一起移动时，对载荷已经离开的区域，细密网格重新划分为粗疏网格，而对载荷即将进入的区域，原粗疏网格划分为细密网格。在网格重划分前后，新旧网格模型的节点占据相同的几何空间，其他场变量，如应力应变实现相应的传递，以使分析求解得以连续进行下去。国内外学者对于该方法已发表了相应的研究成果。Brown等［1］结合网格重划分和动态子结构技术，采用壳体单元分析了平板激光焊接后的变形和应力，所使用的时间与常规的热弹塑性计算相比，仅为后者的1/7，在保证精度的前提下大幅提高了效率，其分析局限于热载荷作用。Huang等［2］以热弹塑性有限元法为基础开发了网格重划分技术来预测线加热过程中板的变形，并应用于三维问题的分析，但载荷形式单一，也未涉及网格划分的分析。Alsamhan等［3］利用实时网格重划分技术，数值模拟了薄板局部滚压成型过程，并通过实验对比了薄膜应力分布，二者吻合较好，成功提升了预测效率，虽然在接触非线性下采用实时网格进行了处理，但对细密网格划分与变形结果尚未开展讨论。另外，关于网格重划分方法中的网格重划分频度，即在载荷作用路线上，一次计算的细密网格区域预先需要选择划分的次数及其在数值计算中的影响，在目前的研究中相对讨论较少。

综上所述，且考虑到关于热载荷移动的研究结果相对较多，本文将重点考虑力载荷接触变化作用条件下的网格重划分数值方法，并主要研究采用不同细密网格尺寸和不同频度的网格划分对计算结果的影响。这里，细密网格尺寸均指载荷作用区域的细密网格区域中网格大小；而网格重划分频度则指这一细密网格预先划分的数量。在此讨论的基础上，本文选择船舶金属板材滚压加工成型进行计算分析，研究接触非线性计算、计算效率及精度与细密网格尺寸和频度的关系。通过滚压加工成型实例，验证细密网格尺寸和网格重划分频度对结果的影响。

1　网格重划分数值方法

网格重划分数值方法的基本思想如前所述。假想存在一块区域，它与载荷速度一致，当网格单元落入该封闭区域时将实现细密的网格划分，而远离封闭区域则划分得相对粗疏（图1），从而能够达到缩小整体刚度矩阵规模的效果。那么在两次网格划分之间，上一步的子模型形状和相关的场变量等数据需要传递到下一步计算的子模型中。考虑到分析的连续性与精确性，变化的网格形状必须要准确模拟，即保证前后网格节点占据相同的几何空间，而相关的场变量要顺利地实现映射，这样才能保证计算结果的精度。具体示意图如图1所示。

网格疏密位置的变化、节点单元编号的改变导致有限元网格模型需不断重新构建。为了匹配下一步网格模型节点在上一步网格模型中的位置，判断节点具体处于哪一个单元内部成为问题的关键。不论是二维模型，还是三维模型均可采用Murti的判断方法［4］。以八节点三维六面体单元为例，如果点在单元内部则满足

式中：i为单元面数；ai，bi，ci如图2所示。如果点不在单元内部，则Vi为负向量，Vi为0则表示点在单元边界上。

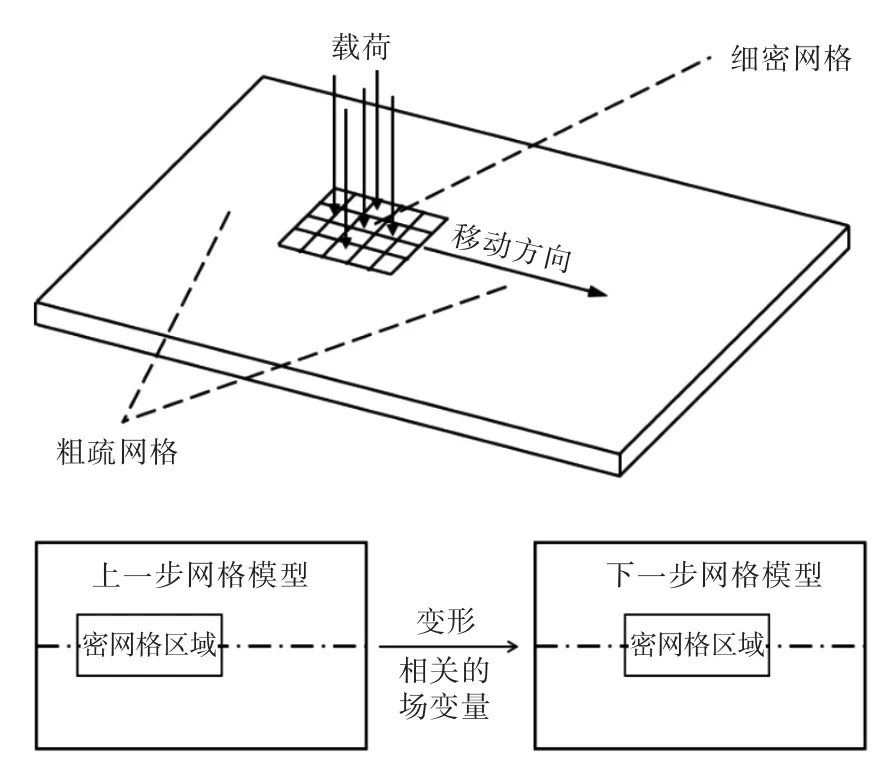
图1　网格重划分和数据传递示意图Fig.1Rezoning and data transfer

图2　空间点的位置Fig.2A spatial point either inside or outside an element

根据等参元的性质和六面体单元形函数Ni，单元中任意一点处的整体坐标满足

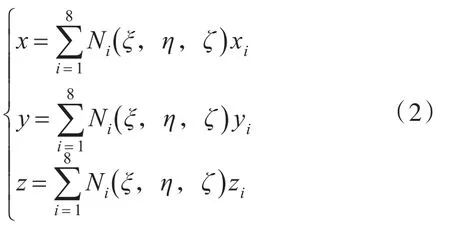
式中：x'y'z为整体坐标系的坐标值；ξ，η，ζ为局部坐标系的坐标值。已知上一步网格模型单元八节点坐标值和位于该单元中一点的坐标，采用Newton-Raphson方法求解得到局部坐标系中的坐标［5］。

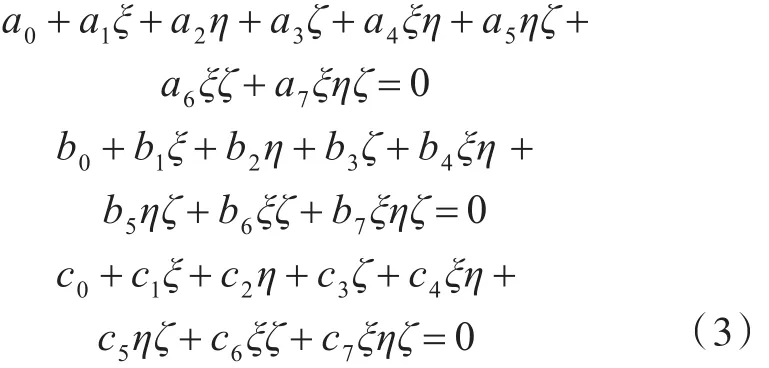
式中，ai，bi，ci为各节点坐标的函数。最后利用形函数对节点位移进行插值，从而得到网格模型的节点在整体坐标系中的坐标值。相关场变量的传递则采用有限元软件的变量映射功能，映射算法中采用插值技术将上一步网格中的残余应力和塑性应变等变量外插到每一个单元节点上，然后对所有相邻同一节点的单元变量取平均；新网格的积分点位置由旧网格的积分点来确定，先找到该点所属旧网格的单元，这样可以确定该点在单元中的位置，变量由旧网格的节点内插到新网格的积分点上［6］。这样就可以保证分析的连续性和准确性。

对于力载荷接触变化作用在板上时，由于非线性响应特征明显，一般需要将网格细密划分才能保证计算的精确性；当力载荷作用深度加大且接触区域面积变大时，细密网格面积也相应地要增加且密度也要加大，才能有利于接触点对的建立，使计算分析成功。因为在接触问题的有限元计算中，通常将接触界面上的面称为接触块，被动接触块上的节点和主动接触块与其接触的点构成一个接触对。那么接触点对的搜寻与合理建立是保证有限元分析结果可靠的关键。如果施载体，即主接触体是刚体，那么作为变形体板壳的受载体，即从接触体的网格必须细密划分，以适应刚体施载过程中接触形状的不断变化。倘若网格比较粗疏，对于较大的载荷量，施载体进入受载体的深度以及接触面积就会相应加大。主接触面单元就会侵入从接触面，导致计算失准，甚至无法继续分析下去。由于施载条件的变化，主、从接触面上的变化如图3所示，图3（a）所示为由于从接触面的网格比较粗糙，主接触面上的单元侵入了从接触面；图3（b）所示为从接触面的网格细化后，就防止了主接触面的侵入［7］。

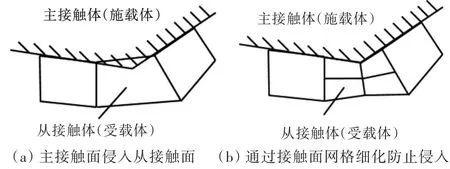
图3　主、从接触面上的变化Fig.3The change of master and slave contact surface

从另一方面讲，即使选择了保证不同载荷深度和大小都适当的网格密度，也还存在一个预先细密网格区域划定多大的问题。

由于密网格区域长度决定了需要多少次对网格模型重划分才能完成一次数值模拟，所以频度大小会影响数值模拟计算效率，频度越小，实际上就越接近于完整模型。另外，频度过大，则由于传递次数过多将导致精度损失，影响计算的精确性；反之则减少精度损失。

通过以上分析，对于板壳而言：

1）载荷增加，接触面积增大，那么载荷区域的网格就需要细化，倘若细密网格尺寸过大，会造成计算失效，但细密网格尺寸太小又会导致计算时间冗长，效率低下；

2）载荷增加，接触面积增大，每一步网格重划分模型的加载区域长度就要相应增加。如果划分频度过小，会造成计算效率降低，而划分频度过大又会造成精度损失。

2　计算结果与分析

本文选择了船舶金属板成型加工方式中常用的局部滚压成型进行计算。具体滚压成型过程是将板材于一对上下凹凸的滚轮中通过，通过给上滚轮施压并随着下滚轮的回转，依靠摩擦将板材向前送进，从而形成变形。在该成型加工过程中涉及接触非线性和滚轮持续稳定的移动载荷作用，该工程对象从受力特征上是典型的在移动线载荷作用下非线性响应的板。选择此工程对象进行网格重划分数值方法应用计算分析具有代表性。矩形钢板模型的尺寸为2 000 mm×1 000 mm×20 mm，材料性质设为理想弹塑性模型，弹性模量为2.09× 105MPa，泊松比为0.3，屈服应力σY=400MPa。

局部滚压加载装置主要包括上滚轮和下滚轮。其中上滚轮为下压轮，尺寸最大半径120 mm，轮毂厚度为200 mm；下滚轮尺寸最大半径160 mm，轮毂厚度为240 mm；上滚轮和下滚轮的具体形状如图4所示。

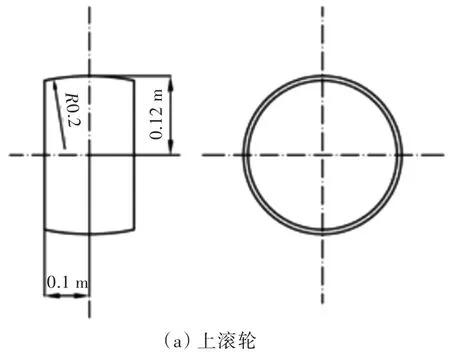
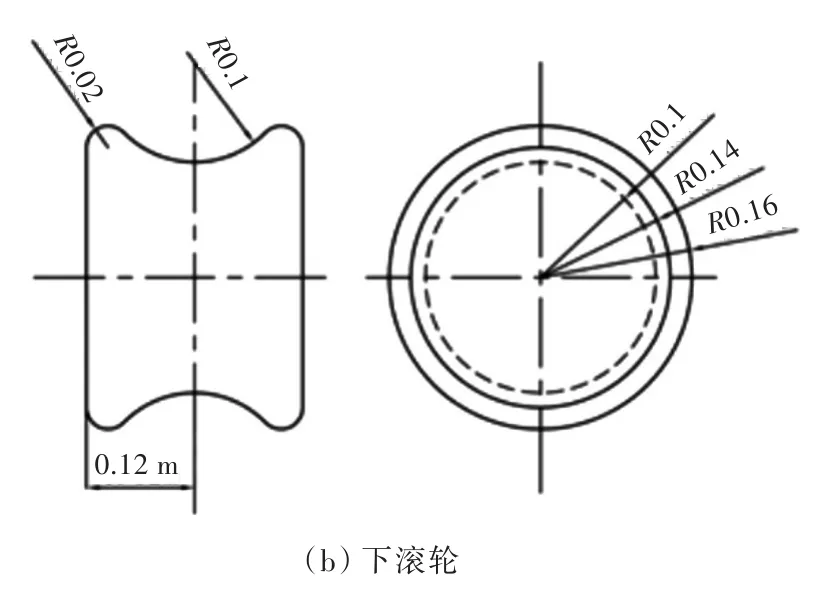
图4　上滚轮截面和下滚轮截面形状Fig.4The section shape of upper roller and lower roller

滚压过程的有限元模型如图5所示，上滚轮和下滚轮简化为刚体，滚压线位于板宽中间位置。加载方式选择施加位移，即给上滚轮一定的下压量进行加载。

图5　常规有限元计算滚压模型Fig.5Conventional FEM roll model

数值模拟步骤为：从板的一端接触→下压→连续匀速滚压→板的另一端卸载。

即接触过程为上滚轮下压建立接触，然后给定下压量，滚压过程是通过下滚轮顺时针旋转带动板材来实现，同时为方便计算选择让板材匀速移动。整个滚压过程边界条件为：开始前平板采用远端位移约束，滚压过程中解除位移约束，滚压过程利用平板与滚轮之间的摩擦约束。

下面，分别对细密网格尺寸与网格重划分频度的影响进行计算。其主要研究方案是对细密网格尺寸进行计算，通过不同的下压量和细密网格尺寸大小的组合进行相应计算，而对其中某一种下压量的计算结果就计算效率和计算精度进行综合分析；对于网格重划分频度的计算，选择某一细密网格尺寸，通过不同下压量和频度大小的组合进行相应计算，而对其中一种下压量的完整计算结果就计算效率和计算精度进行综合分析。计算还对常规有限元方法进行了建模计算，以此作为网格重划分计算的比较分析依据。常规有限元计算模型如图5所示。

2.1细密网格尺寸的影响

根据滚轮尺寸选重划分频度为8，而选择4种不同的细密网格尺寸。据前文定义，频度8表示随着载荷的移动，8次重划分网格模型并分别依次通过载荷作用进行计算。根据前期计算调查，对于本次计算模型，细密网格区域的宽度均选为0.3 m较为合适，与完整模型的加载区域宽度一致，过渡区域和远离加载区域的网格也与完整模型保持一致。而沿载荷作用路线方向上的细密网格区域的长度在重划分频度为8的条件下取0.4 m。在上述区域内，分别用4种细密网格进行划分，网格尺寸如图6所示，网格尺寸依次逐渐变大。

Ⅰ：5 mm×10 mm×5 mm

Ⅱ：10 mm×10 mm×5 mm

Ⅲ：12 mm×10 mm×5 mm

Ⅳ：16 mm×10 mm×5 mm

图6　4种细密网格尺寸示意图Fig.6Four fine mesh size

对4种加载区域细密网格尺寸分别采取不同下压量计算，计算结果如表1所示。

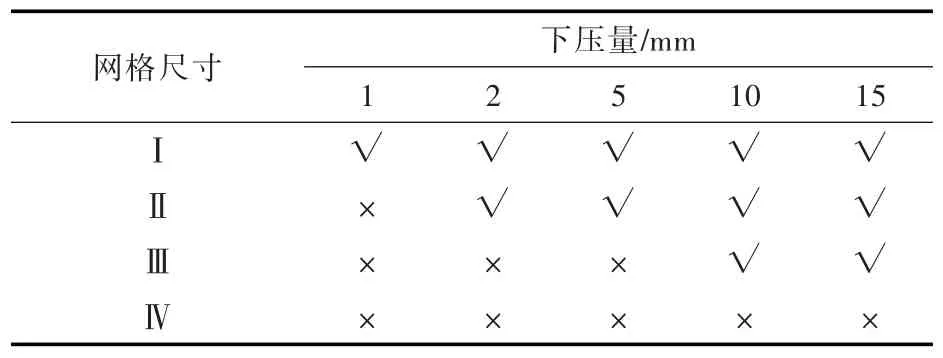
表1　不同下压量下4种网格模型的计算结果Tab.1The results of four models under different amount of depression

从计算结果可知，当细密网格尺寸为Ⅰ时，下压量在1～15 mm都能完成计算；当细密网格尺寸增大至Ⅱ时，下压量在2～15 mm能完成计算；当细密网格尺寸增大至Ⅲ时，下压量在10～15 mm能完成计算；当细密网格尺寸增大至Ⅳ时，下压量在1～15 mm内均不能完成计算。上述结果验证了当载荷区域细密网格尺寸过大时，会造成接触点对的建立无法实现而造成计算失效。

2.1.1计算结果精度

计算结果精度是选取细密网格区域相同的3种不同细密网格尺寸Ⅰ，Ⅱ，Ⅲ与常规有限元模型在下压量为10 mm的计算结果比较来进行的。这里选择滚压0.2 m后板长方向0.1 m处横向中点纵向截面的变形来进行比较，结果如图7所示。

图7　不同细密网格尺寸模型的变形结果Fig.7Final deformation of different fine mesh size models

通过对比发现，3种细密网格尺寸的计算结果略有差别。在细密网格区域相同的情况下，细密网格尺寸越小，变形越接近于常规有限元模型计算变形结果。

2.1.2计算效率

当加载区域细密网格尺寸为Ⅰ时，计算时间平均为60 min；当加载区域细密网格尺寸为Ⅱ时，计算时间平均为26 min；当加载区域细密网格尺寸板长方向为Ⅲ时，计算时间约为20 min。选取下压量为5和10 mm，分别就3种网格尺寸Ⅰ，Ⅱ，Ⅲ的其中一步重划分模型计算时间进行比较，结果如图8所示。

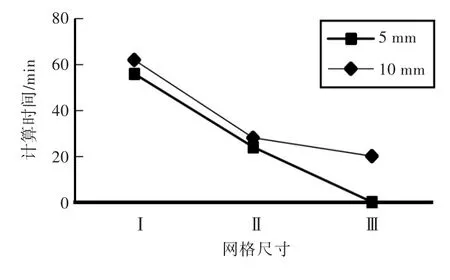
图8　不同细密网格尺寸模型的计算时间Fig.8Computational time of different fine mesh size models

由图可知，在下压量为5 mm时，Ⅱ的计算时间相比Ⅰ缩短了50%，而Ⅲ的计算由于网格尺寸过大而失效；在下压量为10 mm时，Ⅱ的计算时间相比Ⅰ缩短了50%，而Ⅲ的计算时间相比Ⅱ缩短了不到30%。这表明适当增大细密网格尺寸可提高计算效率。如果考虑加工要求，同时又保证数值计算相对高效，细密网格尺寸选择Ⅱ比较合适。

综上所述，加载区域如何选择合适的细密网格尺寸对计算精度和效率都有着重要的影响。细密网格尺寸太小会导致计算时间冗长，效率低下，但精度相对较高；随着细密网格尺寸逐渐增大，会提高计算效率，但会损失精度；如果网格尺寸过大，会导致计算无法进行。

2.2网格重划分频度的影响

本次模拟过程选择细密网格尺寸为10 mm× 10 mm×5 mm的3种不同重划分频度进行计算。如前所述，细密网格区域宽度均仍选定为0.3 m，而沿载荷作用路线方向上的细密网格区域长度根据频度的不同分别取为2，0.8，0.6，0.4 m。有限元网格模型如图9所示，由图9可知模型a，b，c，d分别为频度0，4，6，8的4种重划分模型，其周围网格沿横向和纵向2个方向由密逐步变疏，其中频度为0的重划分模型即为常规有限元计算模型。网格模型参数如表2所示，其中每种频度的重划分模型节点数是相同的。

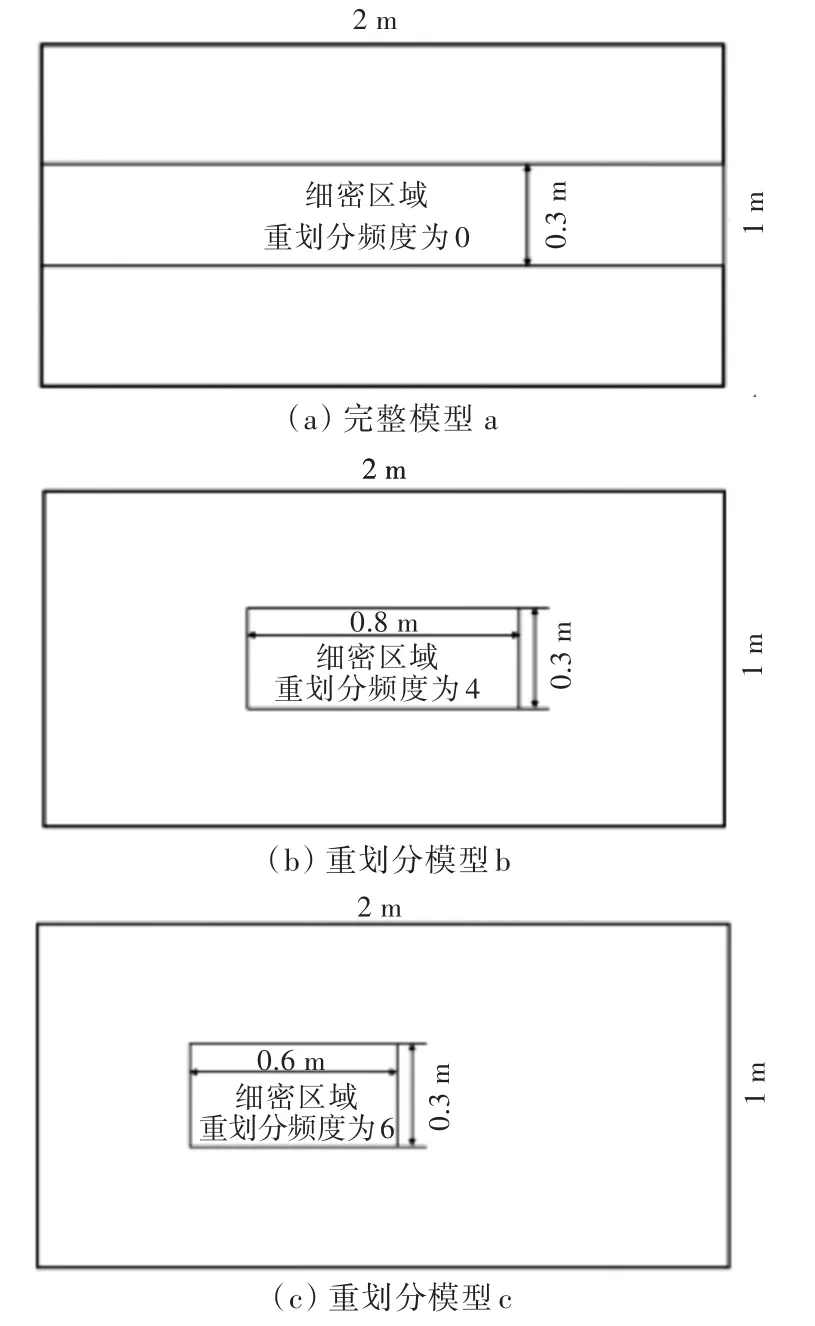
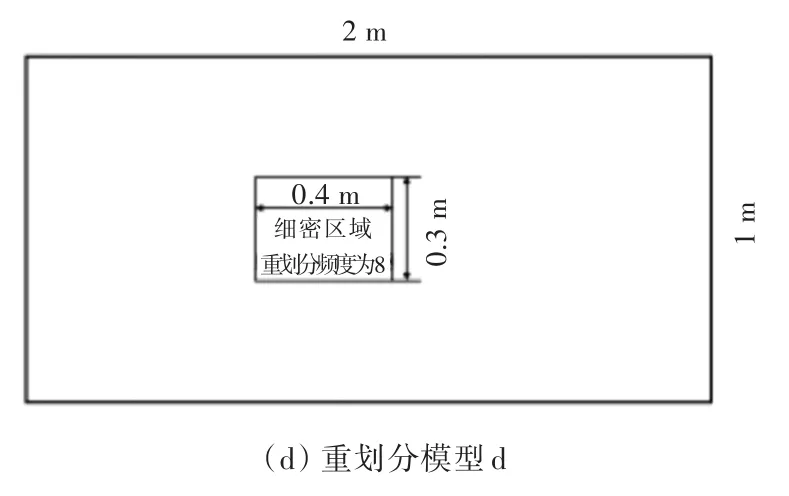
图9　不同频度的有限元网格模型Fig.9FEM models of different frequencies

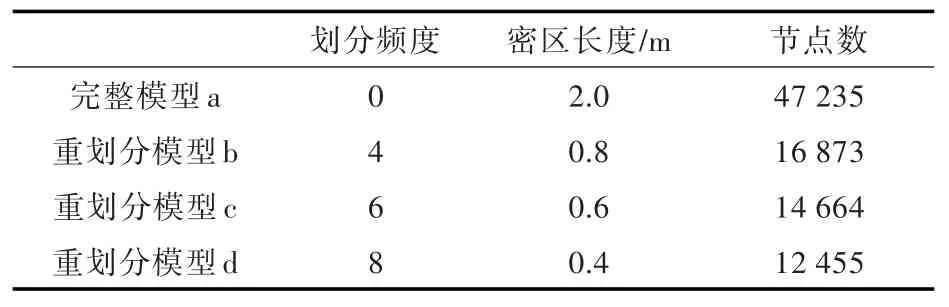
表2　4种不同频度的网格模型参数Tab.2Four models'parameters of different frequencies

2.2.1计算结果的精度

计算结果的精度是通过与频度0完整模型，即常规有限元模型在下压量为5 mm的计算结果进行比较。这里选择板长边方向0.1 m处和中点处的2个横向截面变形以及板横向中点纵向截面的变形来进行比较，如图10所示。

图10　下压量为5 mm时的板材最终变形图Fig.10Final deformation of the plate under depression of 5 mm

由于在板滚压过程中空间位置会变化，为便于比对，将重划分模型的最终变形位置按照完整模型的坐标系进行相应调整。先选取距离加载初始位置0.1和1 m处横截面上的变形结果进行对比，再选取中心线方向纵截面上的变形结果进行对比。计算结果如图11和图12所示。

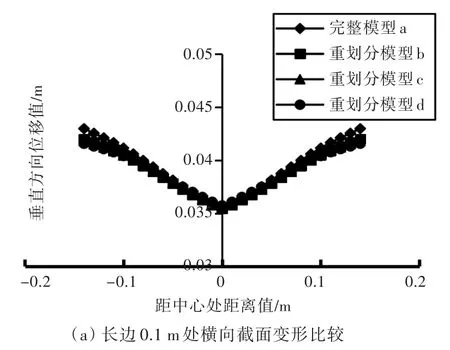
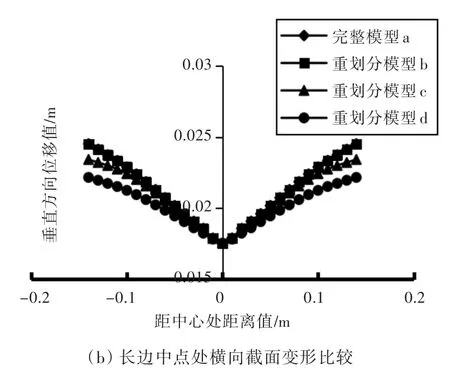
图11　板长边方向横截面上的变形结果比较Fig.11Comparisons of final deformation in the cross section of the plate

图12　板横向中点纵截面上的变形结果比较Fig.12Comparisons of final deformation in the longitudinal section of the plate

由于滚压线为矩形板中心线，所以滚轮沿着滚压线加工矩形板，其变形的形状是对称的。由横向结果对比可以看出：不论是在距离初始位置0.1 m处还是1 m处，完整模型与重划分模型的变形趋势一致，即角变形大小吻合很好，但模型b的变形结果相比于模型c，d来说更接近于完整模型a，不过计算时间要大于模型c，d。两者之间的协调取决于个人需求。中心线方向纵向截面的变形趋势可以说明重划分模型与完整模型的板材最终变形形状是一致的。从变形场的计算结果来看，频度越小，计算效率越低，但精度较高；反之，频度越高，计算效率相对越高，但精度会变差。

平板经过滚压载荷作用，由于存在卸载过程，载荷区域一定会存在较大的残余应力。以下压量5 mm的计算结果为例，完整模型和频度为8的网格重划分模型d的最终应力场计算结果的对比如图13所示。

从图中可以看出，网格重划分数值方法仍然再现了残余应力结果，残余应力分布与常规有限元的计算结果相近，不过相对而言网格重划分数值方法所得塑性应力略微偏大，这是由于网格变化过程中力学信息的传递存在一定的计算误差。

图13　最终残余应力对比Fig.13Comparisons of final residual stress of the plate

2.2.2计算效率

完整模型与网格重划分模型的计算时间如图14所示。将3种不同下压量下完成该次滚压模拟的计算时间进行对比。

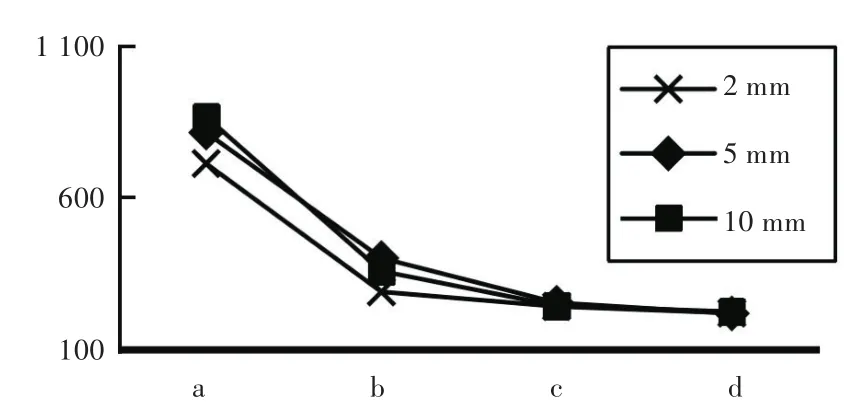
图14　不同频度下模型的计算时间Fig.14Computational time of different frequencies'models

从图中可以看出，使用网格重划分数值方法后，相对于完整模型，重划分模型b的计算时间减少了约57%；网格重划分模型c减少了约66%；重划分模型d减少了约70%。其原因是网格重划分模型中的节点数明显少于完整模型的节点数，也即模型中总的自由度数前者少于后者，那么总体刚度矩阵规模也减少，内存的需求也必将因网格重划分数值方法而得以减少，计算效率因此大幅提高。上述计算结果表明，网格重划分数值方法可以很好地解决效率问题，频度越小，计算效率越低；反之频度越高，计算效率相对越高。

3　结论

本文对网格重划分数值方法中细密网格尺寸与网格重划分频度对移动线载荷作用于板的数值模拟效率和精度的影响进行了研究。以板滚压加工成型数值模拟为例，讨论了4种细密网格尺寸在不同下压量下对效率和精度的影响，并采用不同频度的网格重划分数值方法进行了对比。主要结论如下：

1）由于接触深度和接触区域受载荷作用的影响，要保证获得计算结果，载荷量增加，则网格划分要细密且细密网格区域要增大；当细密网格尺寸变小，计算精度变高但计算效率变低时，细密网格划分的尺寸大小要根据实际加载情况综合考虑。

2）在保证精度的前提下加大网格重划分频度会大幅提高效率，重划分频度越高，会在一定程度上提升效率，但会损失精度，所以频度的大小也要根据综合要求来选择。

3）在适当的网格划分条件下，网格重划分数值方法总的来说可以实现，其在保证精度的前提下相比常规数值计算方法在计算效率上有大幅度提高，可以作为在移动线载荷作用下局部非线性响应问题的有效计算手段。

［1］BROWN S B，SONG H.Rezoning and dynamicsubstructuringtechniques in FEM simulations of welding processes［J］.Journal of Engineering for Industry，1993，115（4）：415-423.

［2］HUANG H，SERIZAWA H，WANG J C，et al.Development of thermal elastic-plastic fem for line heating with remeshingtechnique［J］.Quarterly Journal of the Japan Welding Society，2013，31（4）：134s-137s.

［3］ALSAMHAN A，HARTELY P，PILLINGER I.The computer simulation of cold-roll-forming using FE methods and applied real time re-meshing techniques［J］.JournalofMaterialsProcessingTechnology，2003，142（1）：102-111.

［4］MURTI V，VALLIAPPAN S.Numerical inverse isoparametricmapping in remeshing and nodal quantity contouring［J］.Computers&Structures，1986，22（6）：1011-1021.

［5］黄辉，赵耀，袁华，等.三维网格重划分技术及其在焊接数值模拟中的应用［J］.舰船科学技术，2011，33（5）：120-125. HUANG Hui，ZHAO Yao，YUAN Hua，et al.Research on three-dimensional rezoning technique and its application in simulation of welding［J］.Ship Science and Technology，2011，33（5）：120-125.

［6］HIBBITT D，KARLSON B，SORENSON P.ABAQUS：analysis user's manual：V6.11［M］.Dassault systemes，2011.

［7］王勖成.有限单元法［M］.北京：清华大学出版社，2003：666-694.

Rezoning method in nonlinear simulation of plate under moving load

LI Yuantai1，ZHAO Yao1，YUAN Hua1，WANG Bo2
1 School of Naval Architecture and Ocean Engineering，Huazhong University of Science and Technology，Wuhan 430074，China
2 Wuchang Shipbuilding Industry Co.Ltd，Wuhan 430064，China

Ship building includes line heating，welding，local roll forming and other processing methods for plates.Compared to the plate dimensions，the region under steady moving linear load in the processing method is narrow with highly nonlinear characteristics.How to coordinate the relationship between the process parameters and the response is one of the main contents of the process.Since the linear load moves on the plate，the characteristics of local nonlinear response keep changing continuously，demanding complicated calculations.Because the mesh for the global region under linear load should be fine，conventional numerical methods result in low efficiency.When considering that other regions away from the loading area in the processing remain weak，nonlinear or elastic，the mesh for the region under current loads can be fine，while the mesh for another region away from the load may be relatively coarser in numerical simulations，with fine mesh moving along with the moving loads，i.e.the rezoning numerical method，which can save much computational time.In this paper，the impact of fine mesh size and rezoning frequency on the numerical computation，and the relationship with numerical accuracy and computational efficiency were researched using this method.The numerical computation example of the local rolling forming process was carried out，resulting in the impact of fine mesh size and rezoning frequency on the computational efficiency and numerical accuracy of the rezoning numerical method.The efficient numerical computation means of plates under moving linear loads with local nonlinear response verify the effectiveness of the method.

moving load；rezoning frequency；fine mesh size

U671.3

A

10.3969/j.issn.1673-3185.2016.05.010

2016-03-04网络出版时间：2016-9-21 13:39

国际科技合作专项项目（2012DFR80390）

李元泰，男，1990年生，硕士生。研究方向：数值计算方法研究。

E-mail：xyt_lee@hust.edu.cn

赵耀（通信作者），男，1958年生，教授，博士生导师。研究方向：结构静动态响应和企业信息化研究。E-mail：yzhaozzz@hust.edu.cn