基于Monte-Carlo法预测氯盐渍土地区混凝土结构的使用寿命

荆 磊,闫长旺,刘曙光,张 菊,段连钧

(1. 内蒙古工业大学 矿业学院,呼和浩特 010051; 2. 包头市排水产业有限责任公司，包头 014030)



应用技术

基于Monte-Carlo法预测氯盐渍土地区混凝土结构的使用寿命

荆 磊1,闫长旺1,刘曙光1,张 菊1,段连钧2

(1. 内蒙古工业大学 矿业学院,呼和浩特 010051; 2. 包头市排水产业有限责任公司，包头 014030)

为预测氯盐渍土地区混凝土结构的使用寿命，采用试验方法与数值模拟方法，统计分析了混凝土保护层中氯离子扩散性特征，采用Monte-Carlo法对Fick第二扩散定律进行数值模拟，评估不同保护层厚度混凝土结构的使用寿命。结果表明:氯离子扩散性特征较好地服从正态分布，保护层厚度对混凝土结构使用寿命有明显的影响，适当增加保护层厚度可使结构使用寿命得到显著提高。

普通混凝土；氯盐渍土；Fick第二扩散定律；Monte-Carlo法；使用寿命

我国氯盐渍土环境十分广泛，在该环境中，氯离子可侵入混凝土内部，使钢筋表面的钝化膜被破坏，引起钢筋锈蚀[1-2]。有调查表明，大多数工业建筑达不到设计使用寿命就提前退出服役[3-4]。张立明[5]等的研究表明，我国内蒙古、青海、新疆、西藏等地区，建筑结构物破坏的主要原因是氯盐侵蚀导致钢筋锈蚀，且西部地区盐渍土中的氯离子浓度较海洋坏境中的明显高出很多。因此，研究我国西部氯盐渍土地区混凝土的氯离子扩散性能，建立合理的混凝土结构使用寿命模型具有十分重要的科学价值和现实意义[6]。目前，国内外学者对混凝土中氯离子扩散性进行了深入研究，许多学者认为Fick第二扩散定律可以作为研究混凝土中氯离子扩散性的基本模型，但是需要针对实际情况对其进行合理修正。余红发[7-8]经过严密的数学推导建立了多因素作用下氯离子扩散方程，但在应用时将方程中参数作为确定值考虑，建立的模型为确定性模型，不容易准确反映模型参数的随机性。科学合理的氯离子扩散模型应是建立基于参数不确定性的概率模型，需对模型中主要参数进行随机化处理[9-11]。

本工作采用高浓度氯盐溶液浸泡混凝土试件，模拟氯盐渍土环境对混凝土保护层的侵蚀作用，基于试验结果，分析混凝土中氯离子结合能力，对流区、扩散区、试件表层的氯离子含量，扩散系数随时间衰减性，统计扩散性特征，利用Monte-Carlo法预测混凝土结构的寿命。

1　试验

试验采用尺寸为100 mm×100 mm×100 mm的C35级混凝土立方体试块，五面用防水胶密封，留一面作为氯盐侵蚀面。试验溶液为15%(质量分数)NaCl溶液。浸泡56,112,168,224,280,336 d后，由侵蚀深度方向对试块进行研磨取样，1 cm侵蚀深度内，每2 mm取样，1 cm侵蚀深度外，每5 mm取样，根据JTJ 270-1998《水运工程混凝土试验规程》进行自由氯离子和总氯离子含量测试。

2　结果与讨论

2.1氯离子含量和总氯离子含量

由图1可见,自由氯离子含量和总氯离子含量在混凝土中的分布规律相似，随侵蚀深度的增加，均表现出先增大后降低的趋势，在距混凝土表面一定深度处存在峰值含量。

2.2氯离子结合能力及其统计特征

由于水泥石中C3A(铝酸三钙)的存在，氯离子在混凝土中扩散时会与水泥水化产物发生结合作用，生成3CaO·Al2O3·CaCl2·10H2O(Friedel盐)，使混凝土孔隙溶液中的自由氯离子(Cf)数量减少，一部分氯离子以结合氯离子(Cb)的形式存在，降低了氯离子的扩散速率， 总氯离子含量(Ct)与Cf、Cb的关系为：

(1)

由式(1)可得：

(2)

定义混凝土中氯离子结合能力R为：

(3)

由图2可见，试验数据点大致位于同一直线上，建立关于Cf、Cb的一元线性回归模型，即混凝土中氯离子满足线性结合机制，Cb=RCf，回归结果如表1所示。

由图3可见，图中直线为y=σx+μ，式中,μ、σ分别表示R的均值与标准差，若R值分布在直线附近，可大致判定R服从正态分布，再通过Jarque-Bera检验进一步确定R是否服从正态分布。Jarque-Bera检验是一种正态性检验方法，其原理是根据正态分布的偏度系数S和峰度系数K构造一个自由度为2的卡方分布统计量JB，如式(4)所示。

(4)

2.3对流区深度及其统计特征

将侵蚀表面到峰值的这段区域定义为氯离子对流区，其深度称为对流区深度(Xc)，由于该区域距外界环境较近，氯离子的扩散受外界环境影响较大，可认为该区域氯离子的扩散规律不服从Fick第二扩散定律，考虑将扩散面内移至峰值所在表面。图4表明,对流区深度有随浸泡时间增加而向内移动的趋势，造成这种情况的可能原因是：随着浸泡时间的增加，混凝土表面裂化程度加深，表层混凝土逐渐丧失抵抗氯离子侵蚀的能力，导致峰值向内移动，各浸泡时间Xc的统计值见表2。

图5所示Xc值分布在直线y=σx+μ附近，其中μ、σ分别表示Xc的均值与标准差，可大致判定Xc服从正态分布。同时，依据式(4)计算得Xc统计量JB=0.620 5，小于5.99，Jarque-Bera检验结果进一步表明Xc不拒绝服从正态分布。

2.4扩散区及扩散区氯离子含量的统计特征

将对流区之后的区域定义为扩散区，两个区域交界处的氯离子含量定义为扩散区氯离子含量(Csc)，Csc值为氯离子含量的峰值，各浸泡时间的Csc统计值见表3所示。

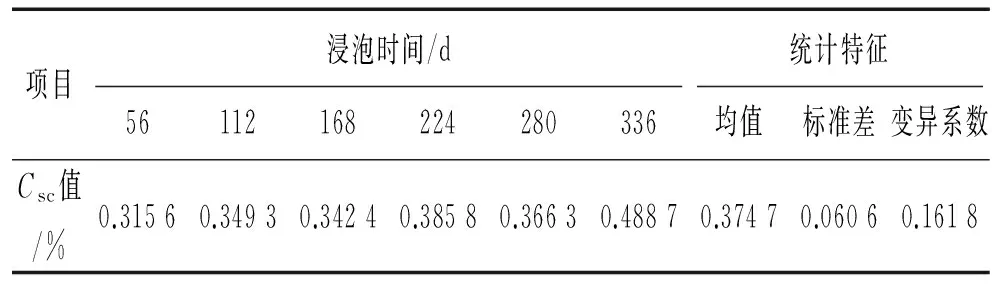
表3　Csc的统计值Tab. 3　The statistic value of Csc

图6所示Csc值分布在直线y=σx+μ附近，其中μ、σ分别表示Csc的均值与标准差，可大致判定Csc服从正态分布。再依据式(4)计算得Csc统计量JB=0.981 3，小于5.99， Jarque-Bera检验结果进一步表明Csc不拒绝服从正态分布。

2.5混凝土表面氯离子含量的变化规律

氯离子在混凝土中传输的主要动力是表面氯离子含量(Cs)，其值随时间逐渐增大，经过一定时间后趋于稳定，一般是通过不同深度处氯离子含量回归得到的，所以也称Cs为理论上的表面氯离子含量。对对流区的Cf值进行叠加作为表面氯离子含量Cs，结果如表4所示。根据Cs值随时间的变化特征，用对数曲线y=a+blnx拟合Cs值，拟合结果如表5和图7所示，拟合参数a=-1.300 5，b=0.440 2均位于95%上下置信区间内，表明拟合结果可信度较高。

表4　表面氯离子含量CsTab. 4　The surface chloride concentration of Cs

表5　Cs拟合结果Tab. 5　The fitting results of Cs

2.6氯离子扩散系数及其衰减性分析

基于假设：①氯离子的扩散系数是一个常数；②氯离子不与混凝土发生吸附和结合；③混凝土是半无限大的均匀介质，Fick第二扩散定律的扩散方程为：

(5)

根据边界条件：C(0,t)=Cs，C(∞,t)=C0，初始条件：C(x,0)=C0，Fick第二扩散定律的解析解为：

(7)

式中:C为时刻t距混凝土表面x处的自由氯离子含量；C0为混凝土内的初始氯离子含量；Cs为表面氯离子含量；x为侵蚀深度；D为氯离子扩散系数；t为浸泡时间；erf(u)为高斯误差函数。

扩散系数D随深度和时间的变化规律如图8所示，由于早期混凝土的水化作用，浸泡56 d的混凝土扩散系数没有明显的变化规律，故在分析扩散系数一般规律时不予考虑。结果表明:各浸泡时间的扩散系数均沿侵蚀深度逐渐增大，同一侵蚀深度处，扩散系数有随时间衰减的趋势。造成这种情况的可能原因是：①水化作用持续进行使混凝土的孔结构逐渐变密实；②氯离子受到孔隙中阴离子的排斥作用；③混凝土的氯离子结合能力。

Thomas等针对上述情况引进时间依赖性常数m，对扩散系数进行了修正。

(8)

式中，Dt为随时间变化的扩散系数；D0为扩散时间为t0时的基准扩散系数；t0为参考时间；m为时间依赖性常数。用公式(8)拟合D0和m值，拟合结果均位于95%上下置信区间内，表明拟合结果可信度较高，拟合结果如表6所示。

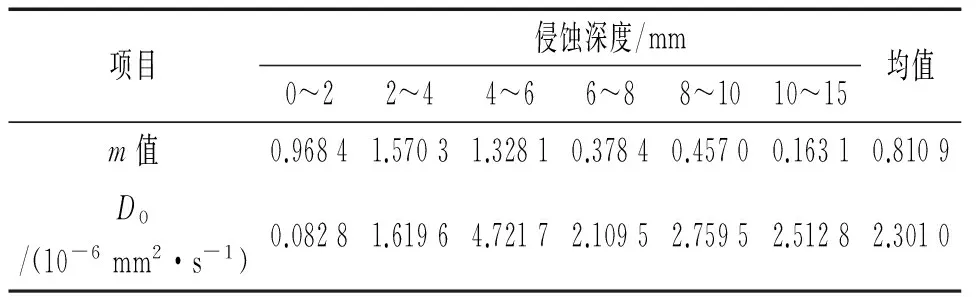
表6　D0、m拟合结果Tab. 6　The fitted results of D0 and m

由表6得到各侵蚀深度处m的均值为0.810 9，D0的均值为2.301 0×10-6mm2/s，利用公式(8)计算衰减后氯离子的实际扩散系数Dt，计算结果如表7所示。图9所示Dt值分布在直线y=σx+μ附近，其中μ、σ分别表示Dt的均值与标准差，可大致判定Dt服从正态分布，并按式(4)计算得Dt统计量JB=1.040 5，小于5.99，Jarque-Bera检验结果进一步表明Dt不拒绝服从正态分布。

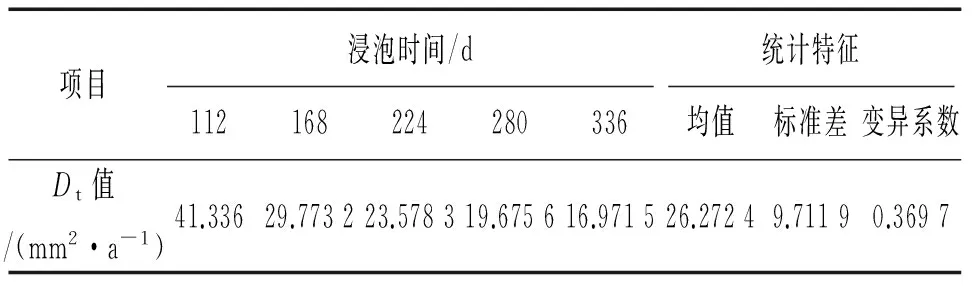
表7　Dt的计算结果Tab. 7　The calculation results of the actual diffusion coefficient

本工作用幂函数曲线y=axb(其中x>0,a>0)对m值进行拟合，拟合得到a=1.296 1，b=-0.314 3，拟合曲线如图10所示，表明当侵蚀深度增加时m值逐渐趋于稳定。

3　混凝土结构使用寿命预测

3.1使用寿命模型

混凝土结构使用寿命的定义：t=t1+t2+t3，t

为混凝土结构的使用寿命，t1为诱导期，t2为发展期，t3为失效期，其中诱导期是指从混凝土遭受氯离子侵蚀至钢筋表面钝化膜被破坏的时间；发展期是指钝化膜被破坏到混凝土保护层开裂的时间；失效期是指混凝土保护层开裂到混凝土结构失效的时间。本文主要进行混凝土结构诱导期的预测，将发展期和失效期作为安全储备。

基于Fick第二定律，当x=d(混凝土保护层厚度)，C=Ccr(钢筋锈蚀的临界氯离子含量)时，由公式(6)可解出混凝土诱导期使用寿命：

(9)

公式(9)中erfc(u)=1-erf(u)，若模型考虑对流区深度Xc，扩散区氯离子含量Csc，氯离子结合能力R，衰减后的实际扩散系数Dt，并假设初始氯离子含量C0=0，则由公式(9)可得式(10)。

(10)

3.2Monte-Carlo法预测结果

采用Monte-Carlo法预测混凝土的使用寿命，公式(10)中各参数的统计特征已有上文给出，临界氯离子含量Ccr取胶凝材料质量的0.52%[11]，混凝土保护层厚度d依次取10 mm、15 mm、30 mm，模拟次数分别为2 000次、2 000次、5 000次，模拟结果如图11所示。结果表明，当d=10 mm时，混凝土使用寿命达到1 a左右的频数最高；当d=15 mm时，混凝土使用寿命达到10 a左右的频数最高；当d=30 mm时，混凝土使用寿命达到50 a左右的频数最高，说明使用寿命对混凝土保护层厚度较为敏感，适当增加保护层厚度可延长氯离子的扩散距离，延缓钢筋表面氯离子含量达到临界氯离子含量的时间，使混凝土使用寿命得到显著提高。

4　结论

(1) 混凝土保护层中，氯离子结合能力R，对流区深度Xc，扩散区氯离子含量Csc，衰减后的氯离子实际扩散系数Dt都较好的服从正态分布。

(2) 混凝土结构使用寿命对保护层厚度比较敏感，适当增加保护层厚度可明显提高混凝土结构使用寿命。

[1]陈小平,王向东,李玉素,等. 氯离子环境下混凝土钢筋的锈蚀过程[J]. 腐蚀与防护,2011,32(3):190-192.

[2]陈伟,许宏发. 盐渍土对钢筋混凝土结构物耐久性设计的影响[J]. 工程结构,2004,24(5):69-73.

[3]金伟良,袁迎曙,卫军,等. 氯盐环境下混凝土结构耐久性理论与设计方法[M]. 北京:科学出版社,2011.

[4]张萍,郭坤. 西宁火车站下穿隧道钢筋混凝土结构的腐蚀与防护[J]. 腐蚀与防护,2014,35(7):737-741.

[5]张立明,余红发,何忠茂. 盐湖地区混凝土的氯离子扩散性[J]. 中南大学学报(自然科学版),2011,42(6):1752-1755.

[6]乔頔,夏文俊,赵阳,等. 盐渍土环境下氯离子侵入混凝土模型研究[J]. 公路交通技术,2011,28(10):154-158.

[7]余红发,孙伟,麻海燕. 混凝土在多重因素作用下的氯离子扩散模型[J]. 建筑材料学报,2002,5(3):241-247.

[8]余红发,孙伟. 混凝土氯离子扩散理论模型[J]. 东南大学学报(自然科学版),2006,36(增刊):69-76.

[9]刘志勇,孙伟,周新刚. 基于Monte Carlo模拟随机计算的海工混凝土使用寿命预测[J]. 东南大学学报(自然科学版),2006,36(增刊):222-225.

[10]孙丛涛. 基于氯离子侵蚀的混凝土耐久性与寿命预测研究[D]. 西安:西安建筑科技大学,2010.

[11]张倩倩,孙伟,施锦杰. 矿物掺合料对钢筋锈蚀临界氯离子含量的影响[J]. 硅酸盐学报,2010,38(4):633-637.

Service Life Prediction of Concrete Structures in Chlorine Saline Soil Region Based on Monte-Carlo Method

JING Lei1, YAN Chang-wang1, LIU Shu-guang1, ZHANG Ju1, DUAN Lian-jun2

(1. School of Mining and Technology, Inner Mongolia University of Technology, Hohhot 010051, China;2. Baotou Drainage Industry Co., LTD, Baotou 014030, China)

In order to predict the service life of concrete structures in chlorine saline soil region, experimental research and numerical simulation were adopted to analyze the chloride ion diffusion characteristics in the concrete cover. Monte-Carlo method was used to simulate Fick′s second law and to assess the service life of concrete structures with different cover thicknesses. The results show that chloride ion diffusion in the concrete cover fairly well coincides with normal distribution. The concrete cover thickness has significant impact on the service life of concrete structures. Appropriate increasing the cover thickness can significantly improve the service life of concrete structures.

ordinary concrete; chlorine saline soil; Fick′s second law; Monte-Carlo method; service life

10.11973/fsyfh-201609012

2015-05-20

国家自然科学基金(51368040); 内蒙古自然科学基金(2015MS0505); 内蒙古自治区高等学校青年科技英才支持计划(NJYT-14-B08)

闫长旺(1978-)，教授，博士，从事混凝土结构耐久性与抗震性能研究，15247179956，ycw20031013@126.com

TU528.1

A

1005-748X(2016)09-0743-05