复杂下垫面风电场风速数值模拟及误差特征

祖繁,樊曙先,王咏薇,吴息



复杂下垫面风电场风速数值模拟及误差特征

祖繁①*,樊曙先①,王咏薇②,吴息②

① 南京信息工程大学 大气物理学院,江苏 南京 210044;

② 南京信息工程大学 大气环境中心,江苏 南京 210044

2012-12-24收稿，2013-08-23接受

江苏省科技支撑计划(BE2010200);江苏省高校优势学科建设工程资助项目(PAPD)

利用WRF模式分别对沿海及山地条件下风电场风速进行高分辨数值模拟,并对其误差特征进行分析,结果表明:1)WRF模式对复杂地形条件下的风速模拟性能良好,模拟值较好地体现天气尺度的周期变化;2)沿海及山地条件下模拟与观测的误差特征各不相同。模式静态数据未能显现沿海的小岛,并且低估了山地测风塔所在的海拔,导致沿海平均模拟风速偏大,山地平均模拟风速偏小;3)分析不同风向的归一化均方根误差,沿海陆风情况下,下垫面相对复杂,误差明显增大;沿海海风情况下,下垫面均一,误差明显减小;4)仅作单个风电场周边数百平方千米的模拟,采用一台12核的服务器进行WRF模式的并行计算可满足48 h短期预测的时效性。仅仅提高模拟的网格分辨率,并不一定能提升模拟的准确性。

复杂下垫面

WRF模式

风速

数值模拟

误差特征

网格分辨率

风力发电作为一种无污染、可再生的能源,已逐渐成为许多国家可持续发展的重要组成部分,发展十分迅速。准确的风速预报可供电网及时调度,从而提高风电的经济效益。但是,由于风具有波动性和间歇性,大容量的风电接入电网将会对电力系统的安全、稳定运行以及保证电能质量带来严峻挑战(王丽婕等,2009)。为促进风电健康发展,保证风电顺利并网和电力系统安全运行,国家能源局[2011]177号文件《风电场功率预测预报管理暂行办法》明确规定,所有风电场需向国家电网调度中心上报短期及超短期风功率预报。通过预测风电场风速,再利用风电场的功率特性曲线,则可转化为预测未来时刻的风力发电功率,这对电力系统合理制定调度计划具有重要的指导意义(Ahlstrom et al.,2005)。

传统的风电场风速预测多采用统计方法,如持续性算法(Alexiadis et al.,1998)、卡尔曼滤波法(卢峰本,1998)、时间序列法(孙春顺等,2008)以及组合预测法(彭怀午等,2011)等。统计方法具有系统误差小的优点,但通常需要大量的、长期的历史测风资料(Ernst et al.,2007),这就为新建风电场的风速预测带来了困难。此外,由于无法描述湍流波动造成的风场突变,统计方法的预测时间尺度也往往在6 h之内,而风力发电并入电网需要风电场至少提供1～2 d的提前预报(Lazar et al.,2010)。由此可见,单纯的统计预测方法并不能满足风电场对风速预测时间长度和预测精度的要求。

目前,数值模式产品在风速模拟预测方面得到了广泛的应用。杨晓玲等(2012)通过ECMWF数值预报格点场资料建立河西走廊东部地区的大风预报方程。吴息等(2004a)使用MM5模式产品预报福建沿海风电场风速并进行误差分析,发现海陆交界下垫面会导致一定的系统性误差。穆海振等(2006)利用TAPM模式对上海近海风场分布的气候特征进行模拟,发现风速大小对下垫面物理特征具有敏感性。孙川永等(2009)使用RAMS模式对某风电场进行了水平分辨率为1 km的短期风速预测,模拟结果能够较好地预报风速风向的变化状况。赵彦厂等(2008)利用RegCM3模式对江苏区域的风场特征进行了分析评估,发现模拟场能够较好地反映风速的空间分布形态。惠小英等(2011)使用WRF模式对酒泉地区进行了风速模拟,并由此给出酒泉风电基地地区风能资源的精细化评估结果。Papanastasiou et al.(2010)利用WRF模式模拟了夏季复杂海岸地形条件下的海风环流特征,模拟结果较好地再现了观测站点风速的日变化特征。

然而数值模式对不同地形条件下的风电场近地层风速模拟的准确性如何?误差特征如何分布?不同网格分辨率对模拟结果的影响如何?同时,数值天气预报方法需要高性能计算机支持计算,计算机的配置、网格分辨率、及时效性与模拟精度如何匹配?这些数值预报问题在风电场风速预测的实际应用中尚需深入研究。

基于以上背景,本文应用WRF模式,对沿海及内陆山地风电场近地层风速进行模拟,并对模拟准确度、误差特征、网格分辨率对计算精度和计算时效的影响等问题进行初步探讨,以期为风电场风电功率预测提供思路。

1　模式及算例

采用WRF模式对沿海及内陆山地复杂地形条件下的风电场风速数值模拟进行研究,分别以已建的福建六鳌及贵州韭菜坪风电场作为研究对象,进行了一个月的风速模拟研究。两次模拟采用相同网格设计的三层嵌套,模拟时间、模拟区域中心及网格设计如表1所示。边界层参数化方案对于近地层风速的模拟至关重要,本文通过多次的个例模拟,选择较优参数化方案,确定沿海模拟选择Monin-Obukhov (Janjic)近地面层方案和MYJ TKE边界层方案,内陆山地模拟选择MYNN近地面层方案和MYNN 3阶TKE边界层方案(Nakanishi and Niino,2004),两次模拟的其他物理过程方案选择相同,即:微物理过程方案选择WSM 3类简单冰相方案;长波辐射采用RRTM方案;短波辐射采用Dudhia方案;陆面过程采用Noah陆面方案;网格格距大于5 km的第一层采用浅对流Kain-Fritsch方案,第二、三层不采用积云参数化方案。模式结果输出时间间隔为1 h。

表1数值模拟设计

Table 1Design of the numerical simulation

模式参数模拟时间模拟区域中心网格数水平分辨率积分时间步长/s垂直分层层顶气压/hPa地形数据初始边界条件沿海2009⁃12⁃01—2009⁃12⁃31116148°E，23962°N第一层：86×48；第二层：97×55；第三层：85×58第一层：9km；第二层：3km；第三层：1km3034层(近地层取密)100USGC全球地形5min、2min、30s6h一次的NCEP再分析资料(1°×1°)山地2010⁃04⁃01—2010⁃05⁃01102．961°E，26．903°N第一层：86×48；第二层：97×55；第三层：85×58第一层：9km；第二层：3km；第三层：1km3034层(近地层取密)100USGC全球地形5min、2min、30s6h一次的NCEP再分析资料(1°×1°)

图1为沿海及内陆山地模拟第三层嵌套范围内的下垫面条件及测风塔位置。A测风塔位于海陆交界点上的一个小岛上,(图2a),小岛约数十米宽,数百米长。WRF模式中最内层30 s分辨率的地形数据,无法有效地分辨出该小岛,所以在WRF下垫面图中,未见该小岛。图1b为模式中贵州韭菜坪风电场下垫面分布。由图可见,韭菜坪风电场下垫面为山地地形,B测风塔位于山脊上,其南侧地形陡峭。对比高分辨率地形图(图2)可见,测风塔所在位置实际地形高度为2 600多米,而在模式中,1 km网格分辨率代表1 km平均的地形高度在2 500 m左右。

2　WRF模式对复杂地形风电场风速模拟性能的量化评估

WRF模式为新一代中尺度天气模式,在天气过程预测、模拟等研究及业务工作中性能良好,然而对于复杂地形的近地层风速模拟性能如何,还需要准确的量化评估。为检验模拟效果,针对福建六鳌风电场以及贵州韭菜坪风电场1个月的模拟结果,采用距离加权反比法将测风塔周围四个格点上的模拟值插值到测风塔上,然后再将其与观测值进行比较。

图1　模拟最内层区域的土地利用及地形高度分布(单位:m;色标从左向右依次代表:灌溉耕地和草地、耕地林地混合、灌丛、落叶阔叶林、常青针叶林、水体和湿地;实三角分别代表:A为福建六鳌风电场测风塔、B为贵州韭菜坪风电场测风塔。)　　a.沿海;b.山地Fig.1　Land use(shaded) and terrian height(contours;units:m) in the innermost domain of (a)coastal areas and (b)mountain areas(colors from left to right represent irrigated cropland and pasture,cropland/grassland mosaic,shrubland,deciduous broadleaf forest,evergreen needleleaf forest,water bodies,and wooded wetland,respectively;the solid triangle A represents the wind tower of the wind farm in Liuao,Fujian;the solid triangle B represents the wind tower of the wind farm in Jiucaiping,Guizhou)

图2　六鳌测风塔(a)及韭菜坪测风塔(b)的周边地貌Fig.2　Landforms of the area surrounding the wind tower in (a)Liuao and (b)Jiucaiping

图3、图4给出了沿海及山地风电场近地层不同高度(10 m,30 m,50 m,70 m)风速模拟值与观测值的对比。大气边界层中的风速由背景环流及复杂地形条件下的局地风叠加形成,从沿海与山地风电场实测风速的变化特征来看,沿海风电场风速变化以数日为周期的天气尺度背景场的特征明显,叠加在天气尺度背景场上亦有逐日变化的特征。山地风电场的风速比沿海风电场的风速有更多波动,除了天气尺度,日尺度的变化,还呈现明显的阵性特征。

对比模拟与实测风速可见,WRF模式能够较好地抓住背景天气条件变化的影响,无论是沿海风电场,还是山地风电场,模拟值均能够较好地体现以数日为周期的天气尺度风速变化,变化趋势亦与观测较吻合。从局地环流影响的逐日变化过程来看,模拟状况略差,沿海风电场在一些风速峰值阶段,模拟值往往大于观测值,这种趋势在高层更为明显。而山地风电场其模拟值往往小于实测值。周期小于24 h的风速阵性特征,模拟值的捕捉能力较弱。

图3　2009年12月福建六鳌风电场不同高度模拟风速和观测风速的比较　　a.10 m;b.30 m;c.50 m;d.70 mFig.3　Comparison of simulated and observed wind speeds at different heights for the wind tower in Liuao,Fujian December 2009:(a) 10 m;(b) 30 m;(c) 50 m;(d) 70 m

图4　2010年4月贵州韭菜坪风电场不同高度模拟风速和观测风速的比较a.10 m;b.30 m;c.50 m;d.70 mFig.4　Comparison of simulated and observed wind speeds at different heights for the wind tower in Jiucaiping,Guizhou April 2010:(a) 10 m;(b) 30 m;(c) 50 m;(d) 70 m

为量化评估模拟结果与观测值的吻合程度,选择相关系数r、百分比误差E、均方根误差RMSE、一致性指数I(Barna et al.,2000)等统计参数对模拟结果进行评估,结果见表2。沿海条件下,模拟值大于实测值,并且随着近地层高度的增加,模拟值与实测值的平均误差增大,到70 m高度时为1.01 m/s。究其原因,主要是实际测风塔位于海边的一簇小岛上(图2a),而在模拟中,由于分辨率的局限性,小岛并未在模拟下垫面中显示,因此测风塔位置处,模拟下垫面为海表,海表相对平滑,粗糙度小,因而模拟所得风速较大。而山地条件下,模拟值总体小于实测值,这种情况在低层更为明显,10 m高度上模拟值和实测值的平均绝对误差为-1.54 m/s。这主要是因为实际韭菜坪风电场所在位置为高度约2 600 m的山脊上(图2b),然而模型采用1 km网格的分辨率,1 km平均的地形高度约为2 500 m,低于实际地形,因此模拟值低于实测值。

沿海风电场的模拟,随着近地层高度的增加,模拟性能并没有显著提高,出现平均误差增大、30 m以上均方根误差基本恒定和一致性指数减少的现象,但是相关系数增加。这说明,在低层,模拟值与观测值的离散度较小,而在高层,模拟值与观测值的离散度较大,但是趋势更为一致。与MM5/Calmet模式在福建沿海测风塔70 m高度处的模拟结果相比(周荣卫等,2010),本研究模拟结果略优,在70 m高度处的均方根误差为2.18 m/s。

山地条件下,随着高度增加,模拟性能提高明显,相关系数及一致性指数明显增大,而平均误差,百分比误差和均方根误差明显减小。任永健等(2012)对湖北齐岳山测风塔的风速模拟也存在类似的结果,底层10 m高度上的误差最大。究其原因,主要是在山地条件下,由于网格及陆面物理过程的局限性,模式很难真实地分辨实际山地条件下的地形及地貌条件。越往低层,地形及地貌条件越复杂,地形地貌对近地面风场的影响越明显,所以在山地条件下,低层的模拟结果与较高层模拟结果相比较差。

综合图3、图4及表2中统计评估参数的结果可知,WRF模式能够较好地模拟海边风电场及山地风电场近地层天气尺度的风速变化,模拟值能够体现其周期,变化趋势亦与观测较吻合。然而对于周期小于24 h的阵性风速的模拟性能有待提高。总体来说,由于地形分辨率的局限性,沿海风电场所在的小岛在模拟算例下垫面内并未显现,沿海风电场模拟值总体大于实测值。同时由于模式可分辨地形高度低于实际地形高度,山地风电场模拟值整体低于实测值。

3　风速模拟误差

由于模式对复杂地形条件下地形高度及下垫面特征分辨能力有限,数值预报的方法很难对近地面风速完全准确地进行模拟,因此研究模拟值与实测值之间的误差特征将为误差订正、提高预报准确率打下基础。下文将对10 m和70 m高度上误差分布的平均日变化特征,误差分布随风速概率及风向的变化特征进行初步研究。

3.1风速误差分布的日变化

风速的日变化特征与下垫面性质有着密切关联(吴息等,2014b)。图5为福建六鳌风电场、贵州韭菜坪风电场测风塔在10 m和70 m高度上模拟值、实测值及误差的日平均分布。时间范围是09:00至次日08:00(北京时间,下同)。从图中可以看出,沿海测风塔10 m高度上误差为-0.54～0.64 m/s,而70 m高度上误差在0.50～1.68 m/s,逐时的平均模拟风速均大于观测风速;山地测风塔10 m高度上误差范围在0.23～-3.69 m/s,70 m高度上误差范围在0.67～-2.39 m/s,10 m高度上的误差波动比70 m高度上的大,这与10 m高度贴近地面,模拟风速受地形和下垫面粗糙度的影响比70 m处大有关;01:00至次日10:00为山地测风塔一天当中模拟误差最大的时段,10 m误差范围达-2.01～-3.68 m/s,70 m误差范围达-1.16～-2.39 m/s。

3.2风速对误差的影响

图6是沿海及山地测风塔在10 m和70 m高度上观测、模拟风速分布概率分对比。由图6a、6c可看出,沿海模拟风速分布概率高值区较实测风速有右移的现象,70 m高度处尤其明显,导致月平均模拟风速偏大,出现这种结果是边界层方案对下垫面拖曳作用考虑不够充分造成的。山地风速模拟值在高风速区的分布概率较低,导致10 m、70 m月平均模拟风速比观测风速分别小了1.54 m/s和0.73 m/s。山地测风塔位于山脊上,其周围地形陡峭,气流爬坡通过山脊时会由于地形作用而加速,但模式地形为1 km×1 km的平均地形,削弱了实际地形的陡峭程度,故风速模拟值较小。此外,通过对比发现,山地条件风速模拟得到较多的是风速小于1 m/s的风,而实际观测却几乎没有风速小于1 m/s的风。

表2沿海、山地测风塔不同高度上风速模拟结果的统计评估

Table 2Statistical assessment of the simulated wind speeds at different heights for the wind tower in the coastal and the mountain area

测风塔高度/m平均风速/(m·s-1)模拟值观测值误差相关系数百分比误差/%均方根误差/(m·s-1)一致性指数沿海1072371800507276356022608476307957370580750633292180850750834762072075583142219084867085775610107659299721808459山地10576730-1540512847363440670030592728-1360520246253370694450620722-1020542745503250724370638711-07305604417231307413

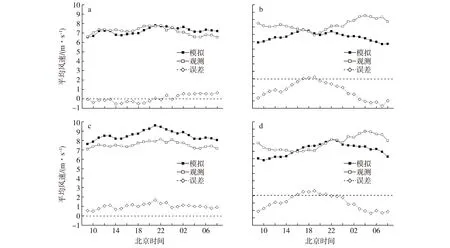
图5　测风塔不同高度上模拟值、观测值及误差的日平均分布　　a.沿海10 m;b.山地10 m;c.沿海70 m;d.山地70 mFig.5　Daily average distribution of simulations,observations and bias at different levels of the wind towers:(a)10 m in the coastal area;(b)10 m in the mountain area;(c)70 m in the coastal area;(d)70 m in the mountain area

图6　测风塔不同高度上实测、模拟风速概率分布对比　　a.沿海10 m;b.山地10 m;c.沿海70 m;d.山地70 mFig.6　Comparison of observed and simulated wind speed frequency distribution at different levels of the wind towers:(a)10 m in the coastal area;(b)10 m in the mountain area;(c)70 m in the coastal area;(d)70 m in the mountain area

3.3风向对误差的影响

为了进一步了解不同风向上风速模拟效果,将各个风向区间范围内的均方根误差进行归一化处理(图7)。其中,若某一风向区间上出现风的概率很小(样本数小于15),则该方向不予统计,由图7a可看出沿海测风塔10 m高度上归一化均方根误差较高的风向为NW-NNW(来自陆地,见图1a),归一化均方根误差较小的风向为NNE-ENE(来自海洋),这说明在沿海WRF模式对海风的模拟性能比陆风的优越。图7b中70 m高度上,归一化均方根误差由NNW到E(陆风转到海风)逐渐变小的现象更加明显。而在内陆山地测风塔处,上下层归一化均方根误差普遍较大(大于等于0.6),10 m高度上归一化均方根误差最大的风向为NNE,70 m高度上归一化均方根误差最大的为SSW和S。

图7　测风塔不同高度上各风向的归一化均方根误差　　a.沿海10 m;b.山地10 m;c.沿海70 m;d.山地70 mFig.7　Normalized RMSE versus wind direction at different levels of the wind towers:(a)10 m in the coastal area;(b)10 m in the mountain area;(c)70 m in the coastal area;(d)70 m in the mountain area

图8　加速比测试Fig.8　Speedup test with multiple threads

4　不同网格分辨率的准确性和时效性

对于持续时间24 h的短期预报来说,数值预报是一种非常有效的办法。然而为了确保数值预报的时效性与准确性,计算机计算性能及网格分辨率如何配置,值得探讨。

采用曙光5U塔式服务器,2颗Xeon 5650(2.67GHz)6核处理器,具备24线程处理能力,内存12 G,操作系统为SUSE Linux,编译器为PGI10.6,并行软件为MPICH2-1.1.1。图8给出了该服务器对福建六鳌风电场风速模拟进行6 h积分的加速比测试结果,使用并行计算可有效地提高模式计算速度,节省积分时间。随着线程数的增加,所需的计算时间快速减少,加速比增加,线程数为12时并行加速比达到最大值5.872,但此后随着线程数的继续增加,计算时间并没有得到提高,并行加速比反而降低。

从风功率预测的时效性保障来说,国家能源总局要求当天上报次日00时至24时的短期风功率预测结果。风速的预测时效需考虑数值模式的初始及背景场数据的下载时间,模拟计算前期融合时段等等多种因素,取48 h为预报长度。分别对福建六鳌风电场及贵州韭菜坪风电场进行48 h的风速数值预报,分9 km、3 km、1 km分辨率。其中,9 km分辨率的模拟只运行原算例设计的第一层嵌套,地形数据变为30 s,其他参数与表1同;3 km分辨率的模拟只运行原算例设计的第一层和第二层嵌套,地形数据分别改为2 min和30 s,其他参数与表1同。1 km分辨率具体情况参见表1及算例介绍部分。不同网格分辨率的测试选择速度最快的12进程数进行模拟,同时使用Linux脚本实现模式前处理、模式计算的自动运行并记录每次运行所需的时间,结果如图9a所示。随着网格分辨率的提升,模拟耗时也在不断增加,3种不同网格分辨率,沿海模拟平均耗时分别为20 min、104 min和367 min,山地模拟平均耗时分别为26 min、105 min和344 min。可见,采用曙光5U12核塔式服务器,即使采用1 km的分辨率也能够满足预报时效性,预报48 h仅需约6 h的计算时间。

进一步探究不同分辨率的模拟精度。由于多数风电场的风机轮毂高度在70 m左右,下文将对沿海及山地70 m高度上9 km、3 km和1 km网格分辨率模拟的平均误差、相关系数以及均方根误差进行分析,结果如图9b、c、d所示。提高网格分辨率,可以增大模拟结果与观测结果之间的相关系数,这在山地尤为明显,但是仅仅提高区域的网格分辨率,并不一定能提升模拟的准确性。例如,在沿海,当网格分辨率由9 km提升至3 km时,模拟准确性也随之提升,平均误差和均方根误差分别减小4.43%和8.50%,而当网格分辨率继续由3 km提至到1 km时,模拟准确性就没有得到进一步提升,均方根误差反而增加了3.03%,这与杨正卿等(2010)进行的格距敏感性模拟试验结果相似,可能与沿海下垫面较平坦有关。因此,在风电场风速预测的实际应用过程中,选择模拟区域分辨率对于寻求准确性与时效性之间的平衡是非常重要的,如果过分的追求网格分辨率,模拟准确性不一定能够得到提升,模拟计算耗时反而会大大地增加。

5　讨论和结论

本文使用WRF模式分别对沿海及山地风电场风速进行了一个月的数值模拟研究,并对模拟的准确性、误差特征以及不同网格分辨率模拟性能等问题进行了探讨,主要结论如下:

1)无论在沿海下垫面还是山地下垫面,WRF模式风速模拟值均能较好地体现天气尺度的周期变化,且其变化趋势与观测值也较吻合,但对周期小于24 h的局地环流及湍流阵性风速特征,WRF模式模拟值的捕捉能力相对较弱。

2)沿海及山地条件下模拟与观测的误差特征各不相同。在沿海,由于模式静态数据并未显现测风塔所在的小岛,模式中测风塔所在的下垫面为海表,对下垫面拖曳作用考虑不够充分,导致平均模拟风速偏大;而山地观测塔位于山脊上,其周围地形陡峭,气流爬坡过山脊时会由于地形作用而加速,但模式的平均地形削弱了实际地形的陡峭程度,导致平均模拟风速偏小。

3)分析不同风向的归一化均方根误差,沿海条件下陆风情况下,由于下垫面相对复杂,误差明显增大;海风情况下,下垫面均一,误差明显减小。该种明显的误差分布特征为沿海风电场风速预报误差订正提供了方向。山地条件下,各方向的下垫面都较为复杂,不同风向的误差分布并无明显特征,数值预报值的误差订正需进一步探究。

图9　沿海及山地条件70 m高度上不同网格分辨率模拟耗时及模拟结果　　a.模拟耗时;b.平均误差;c.相关系数;d.均方根误差Fig.9　Consuming time and results of the simulations with different grid resolutions at 70 m in the coastal and the mountain area:(a)consuming time;(b)mean error;(c)correlation coefficient;(d)RMSE

4)仅作单个风电场周边数百千米的模拟,采用一台12核的服务器进行WRF模式的并行计算可满足48 h短期预测的时效性。山地条件下,地形地貌比较复杂,网格分辨率的提高导致地形地貌的分辨程度增加,模拟精度有所提高。然而沿海条件下,1 km分辨率的模拟并不比3 km的模拟更具优势。仅仅提高区域的网格分辨率,并不一定能提升模拟的准确性,还需要从引入更准确的地形地貌数据。

本文以福建六鳌风电场及贵州韭菜坪风电场作为沿海和山地条件的代表进行风速模拟的数值研究,对数值模拟的精度,误差特征,计算条件与预报时效性以及网格分辨率的匹配做了一初步的探讨。

然而风电场近地层风速的数值预报仍有大量的工作,数值模式的参数化方案的适应性,精细体现风电场实际地形地貌静态数据的引入,大量不同类型风电场观测数据的长期模拟比对等问题尚需深入研究。

References)

Ahlstrom M,Jones L,Zavadil R,et al.,2005.The future of wind forecasting and utility operations[J].IEEE Power Energy Mag,3(6):57-64.

Alexiadis M C,Dokopoulos P S,Sahsamanoglou H S,et al.,1998.Short-term forecasting of wind speed and related electrical power[J].Sol Energy,63(1):61-68.

Barna M,Lamb B,O’neill S,et al.,2000.Modeling ozone formation and transport in the Cascadia region of the Pacific Northwest[J].J Appl Meteor,39(3):349-366.

Ernst B,Oakleaf B,Ahlstrom M L,et al.,2007.Predicting the wind[J].IEEE Power Energy Mag,5(6):78-89.

惠小英,高晓清,桂俊祥,等,2011.酒泉风电基地高分辨率风能资源的数值模拟[J].高原气象,30(2):538-544.Hui X Y,Gao X Q,Gui J X,et al.,2011.Numerical simulation of high resolution wind power resource in Jiuquan wind power base area[J].Plateau Meteor,30(2):538-544.(in Chinese).

Lazar L,Goran P,Momcilo Z,2010.Wind forecasts for wind power generation using the Eta model[J].Renew Energ,35(6):1236-1243.

卢峰本,1998.卡尔曼滤波在沿海冬半年风力预报中的应用[J].气象,24(3):50-53.Lu F B,1998.The application of Kalman filter to the coastal wind forecast in winter[J].Meteor Mon,24(3):50-53.(in Chinese).

穆海振,徐家良,柯晓新,等,2006.高分辨率数值模式在风能资源评估中的应用初探[J].应用气象学报,17(2):152-159.Mu H Z,Xu J L,Ke X X,et al.,2006.Application of high resolution numerical model to wind energy potential assessment[J].J Appl Meteor Sci,17(2):152-159.(in Chinese).

Nakanishi M,Niino H,2004.An improved Mellor-Yamada level-3 model with condensation physics:its design and verification[J].Bound-Layer Meteor,112(1):1-31.

Panastasiou D K,Melas D,Lissaridis I,2010.Study of wind field under sea breeze conditions:An application of WRF model[J].Atmos Res,98(1):102-117.

彭怀午,刘方锐,杨晓峰,2011.基于组合预测方法的风电场短期风速预测[J].太阳能学报,32(4):543-547.Peng H W,Liu F R,Yang X F,2011.Short term wind speed forecast based on combined prediciton[J].Acta Energ Sol Sin,32(4):543-547.(in Chinese).

任永建,刘敏,袁业畅,等,2012.湖北省风能资源的高分辨率数值模拟试验[J].自然资源学报,27(6):1035-1043.Ren Y J,Liu M,Yuan Y C,et al.,2012.The high resolution numerical simulation of wind energy resource in hubei province[J].Journal of Natural Resources,27(6):1035-1043.(in Chinese).

孙川永,陶树旺,罗勇,等,2009.高分辨率中尺度数值模式在风电场风速预报中的应用[J].太阳能学报,30(8):1097-1099.Sun C Y,Tao S W,Luo Y,et al.,2009.The application of high resolution mesoscale model in wind speed forecasting in wind farm[J].Acta Energ Sol Sin,30(8):1097-1099.(in Chinese).

孙春顺,王耀南,李欣然,2008.小时风速的向量自回归模型及应用[J].中国电机工程学报,28(14):112-117.Sun C S,Wang Y N,Li X R,2008.A vector autoregression model of hourly wind speed and its applications in hourly wind speed forecasting[J].Proceedings of the CSEE,28(14):112-117.(in Chinese).

王丽婕,冬雷,廖晓钟,等,2009.基于小波分析的风电场短期发电功率预测[J].中国电机工程学报,29(28):30-33.Wang L J,Dong L,Liao X Z,et al.,2009.Short-term power prediciton of a wind farm based on wave analysis[J].Proceedings of the CSEE,29(28):30-33.(in Chinese).

吴息,黄林宏,周海,等,2014a.风电场风速数值预报的动态修订方法的探讨[J].大气科学学报,37(5):665-670.Wu X,Huang L H,Zhou H,et al.,2014a.Discussion on dynamic corrections of numerical prediction of wind velocity in wind farm[J].Trans Atmos Sci,37(5):665-670.(in Chinese).

吴息,白龙,崔方,等,2014b.海面与海岸陆面风速廓线特征[J].大气科学学报,37(2):138-145.Wu X,Bai L,Cui F,et al.,2014b.Wind profile features of surface layer over ocean and cost[J].Trans Atmos Sci,37(2):138-145.(in Chinese).

杨晓玲,丁文魁,袁金梅,等,2012.河西走廊东部大风气候特征及预报[J].大气科学学报,35(1):121-127.Yang X L,Din W K,Yuan J M,et al.,2012.Climate characteristics of the gale and its forecast in east Hexi corridor[J].Trans Atmos Sci,35(1):121-127.(in Chinese).

杨正卿,刘聪,银燕,2010.苏通大桥桥位江面风速的数值试验[J].气象科学,30(2):193-201.Yang Z Q,Liu C,Yin Y,2010.Numerical experiment of the wind velocity over Sutong highway bridge[J].Scientia Meteorologica Sinica,30(2):193-201.(in Chinese).

赵彦厂,江志红,吴息,2008.基于区域气候模式的江苏省风能评估试验[J].南京气象学院学报,31(1):75-82.Zhao Y C,Jiang Z H,Wu X,2008.Wind energy resource evaluation for Jiangsu province based on RegCM3[J].J Nanjing Inst Meteor,31(1):75-82.(in Chinese).

周荣卫,何晓凤,朱蓉,等,2010.中国近海风能资源开发潜力数值模拟[J].资源科学,32(8):1434-1443.Zhou R W,He X F,Zhu R,et al.,2010.Numerical simulation of the development potential of wind energy resources over China’s offshore areas[J].Resources Science,32(8):1434-1443.(in Chinese).

Accurate wind speed forecasts ensure the timely dispatch of power,thereby improving the economic effectiveness of wind power.The traditional methods of wind speed prediction focus on statistical models,but these are unable to satisfy requirements in terms of precision and time.Numerical models have become more prevalent in wind speed forecasting in recent years.Accordingly,in order to investigate simulation accuracy,error characteristics and time effectiveness for wind speed simulation of a numerical model over a complex underlying surface,one-month long wind speeds at the heights of 10 m,30 m,50 m and 70 m on a wind farm in Liuao (coastal area) and Jiucaiping (mountain area) are respectively simulated using the WRF model.The main results and discussion points are as follows:

(1)The comparison of simulated and observed wind speeds at different heights indicates that the WRF model performs well in simulating the wind speed over a complex underlying surface,the simulated wind speed trends are in good agreement with the observations in both coastal and mountain areas,and the synoptic-scale variations are also well reflected in the simulation.However,the fluctuation caused by the local circulation and turbulence is hard to capture in the wind speed simulation.Besides,statistical assessments using correlation coefficients,relative error,root-mean-square error(RMSE) and index of agreement show that the accuracy of wind speed simulation does not enhance with increased height in coastal areas,but improves significantly in mountain areas.

(2)The error characteristics between simulations and observations are different in coastal and mountain areas.Compared with the real landforms,the small island in coastal areas does not appear in the model’s static terrestrial data.As a result,the frictional effect of the underlying island is neglected in the simulation,and the average simulated wind speeds are overestimated in coastal areas.Nevertheless,the elevation of the wind tower in mountain areas decreases in the static terrestrial data due to the weakening of the actual mountain slope,and thus the average simulated wind speeds are underestimated in mountain areas.

(3)The normalized RMSE of wind speeds is analyzed in different directions.The normalized RMSE increases significantly due to the relatively complex underlying surface in the case of land breezes,and decreases due to the homogeneous underlying surface in the case of sea breezes in coastal areas.Conversely,the normalized RMSE distribution is not obvious in mountain areas.The obvious error distribution characteristics provide a direction for further error correction of wind speed forecasting on wind farms in coastal areas.

(4)To forecast the wind speed on a scale of a few hundred kilometers surrounding the wind farm,parallel computation of the WRF model using a server with 12-core processors is sufficient to meet the time effectiveness of 48-h short-term forecasts.However,only increasing the grid resolution is not necessary to improve the accuracy of the simulation.Therefore,in the practical application of wind speed forecasting on a wind farm,it is important to set an appropriate grid resolution for the balance between simulation accuracy and time effectiveness.More accurate terrestrial data should be introduced to improve the precision.

complex underlying surface;WRF model;numerical simulation;wind speed;error characteristics;grid resolution

(责任编辑：刘菲)

Numerical simulation and error characteristics for wind speed on a wind farm over a complex underlying surface

ZU Fan1,FAN Shuxian1,WANG Yongwei2,WU Xi2

1SchoolofAtmosphericPhysics,NanjingUniversityofInformationScience&Technology,Nanjing210044,China;2AtmosphericEnvironmentCenter,NanjingUniversityofInformationScience&Technology,Nanjing210044,China

10.13878/j.cnki.dqkxxb.20121224001

引用格式：祖繁,樊曙先,王咏薇,等,2016.复杂下垫面风电场风速数值模拟及误差特征[J].大气科学学报,39(5):672-682.

Zu F,Fan S X,Wang Y W,et al.,2016.Numerical simulation and error characteristics for wind speed on a wind farm over a complex underlying surface[J].Trans Atmos Sci,39(5):672-682.doi：10.13878/j.cnki.dqkxxb.20121224001.(in Chinese).

*联系人，E-mail:zufan123@yeah.net