均匀平面阵下的二维DOA估计与互耦自校正*

刘 江，张 辰

（1.中国西南电子技术研究所，成都　610036；2.浙江大学信息与电子工程学院，杭州　310027）

均匀平面阵下的二维DOA估计与互耦自校正*

刘 江**1，张 辰2

（1.中国西南电子技术研究所，成都610036；2.浙江大学信息与电子工程学院，杭州310027）

针对存在互耦效应时均匀平面阵的测向鲁棒性问题，提出了一种基于秩损准则的互耦自校正算法。根据对互耦效应的先验知识，提出的算法只需将受互耦扰动的阵列响应在变换域中重新排列，便可在后续处理中屏蔽掉互耦效应的不利影响，同时也避免了现有工作中存在的阵列孔径损失问题。借助秩损估计原理，在变换域中设计了一种巧妙的计算步骤，使得方位估计的降维操作得以实现；并且，后续还可通过特征分解法得到更精确的互耦系数估计，以进行阵列误差自校正。与现有的研究工作相比，所提算法无论是在估计精度，还是在计算效率上均有着显著的性能优势。

均匀平面阵；到达角估计；互耦效应；自校正；秩损准则

1　引言

利用天线阵对信源到达角（Direction of Arrival，DOA）进行估计的课题在许多领域得到了广泛的研究，比如跟踪雷达、声呐及移动通信等。在过去的20年中也涌现出一系列高分辨率测向算法［1］，但这些算法的有效性大多依赖于精确已知的阵列流形。然而，实际的天线阵中存在着固有的互耦效应，此时理想的阵列流形将不可避免地被未知互耦效应所扰动，若不对其加以考虑的话，高分辨率测向算法的性能会严重恶化，特别是当阵元间距较小时［2］。因此，国内外学者针对互耦效应的校正问题展开了深入的研究［3］。由于互耦效应会随着时间缓慢变化，能在线估计信源方位和互耦系数的自校正算法近年来唤起了学者们的研究兴趣。例如：文献［4-5］主要研究了迭代类自校正算法，但是迭代处理是很耗时的，且全局收敛性也无法保证；此外，另一类不需要迭代的自校正算法在文献［6-7］中被提出来。但是，上述文献研究的都是均匀线阵或圆阵下的一维DOA估计问题，而对于互耦误差条件下的二维DOA估计问题，目前的研究还不是很充足。

在所有可能的阵列配置中，平面阵由于可以在三维空间中进行更灵活的波束扫描，使得目标测向时的联合方位/俯仰角估计成为可能，因此非常适合应用在移动通信中。然而，平面阵中的互耦效应要比线阵和圆阵更加复杂，而关于均匀平面阵下的测向和互耦自校正问题，现有的研究工作却十分有限。为了消除互耦效应的影响，文献［8］将平面阵的外围边界阵元设为辅助阵元，仅利用处于一致耦合环境下中间子阵的输出响应进行处理，此时标准二维多重信号分类（Multiple Signal Classification，MUSIC）算法可直接应用。但这种方法存在着明显的阵列孔径损失，且算法中涉及的二维谱峰搜索计算效率也很低。考虑到上述问题，我们认识到平面阵下的测向、互耦校正精度以及计算效率还可进一步提升。

秩损估计器最初是针对部分校正阵列下的一维方位估计问题设计的［9］，它可以将未知的阵列扰动与阵列流形中已校正的部分巧妙地分离开。在本文中，我们将秩损估计准则扩展到二维场景，并通过变换域处理，提出一种高效鲁棒的互耦自校正算法，可获得更准确的信源方位和互耦系数估计值，便于进行更精准的互耦误差校正。

2　信号模型和问题描述

2.1理想信号测向模型

如图1所示，考虑一个放置在xy平面上的、由M×N个相似元组成的均匀平面阵，其x、y轴方向上的阵元间距分别为dx和dy，不考虑阵元间的互耦效应，则对应（θ，φ）信源方向上的理想导向矢量为

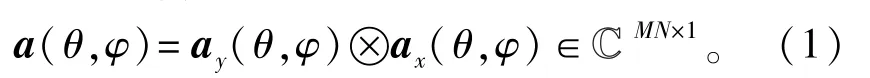
式中：⊗为Kronecker积；θ∈［0，2π）和φ∈［0，π/2）分别是方位角和俯仰角。并且有

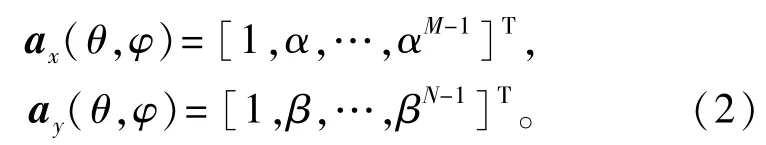
式中：上标T代表转置；α=ej2π/λdxcosθsinφ；β= ej2π/λdysinθsinφ；λ表示信号的载波波长。考虑K个远场窄带信号分别从未知方向｛θk，φk｝Kk=1入射到平面阵上，那么阵列输出响应可被建模为

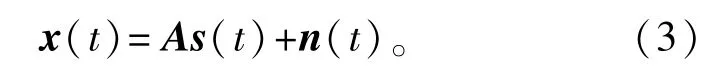
式中：x（t）∈CCMN×1为阵列响应沿x轴方向按列堆栈而成的矢量；s（t）∈CCK×1为相互独立的源信号矢量；n（t）∈CCMN×1是不相关的采样噪声矢量，均值为零，方差为σ2n；而A=［a（θ1，φ1），a（θ2，φ2），…，a（θK，φK）］∈CCMN×K代表理想的阵列响应矩阵。

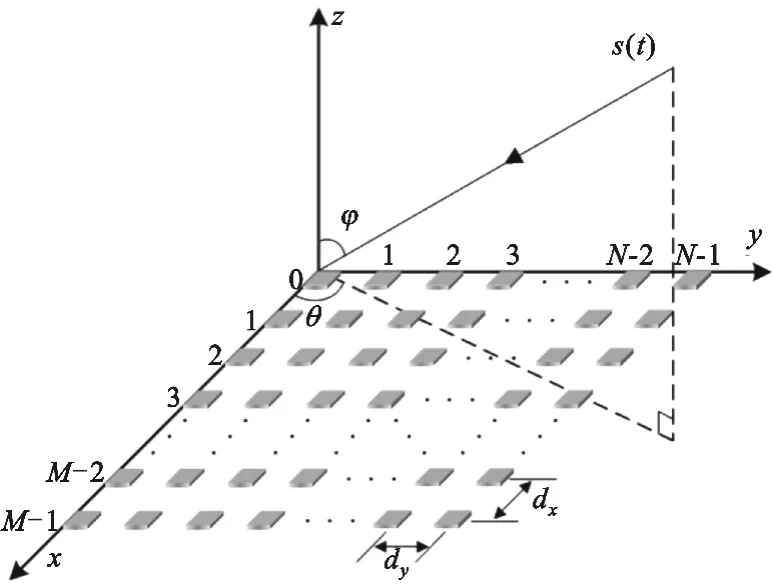
图1　由各向同性阵元构成的均匀平面阵示意图Fig.1 Schematic diagram of uniform planar array composed of isotropic matrix elements

2.2均匀平面阵下的互耦模型

式（3）所表示的无互耦信号模型仅在理想条件下是成立的。在实际天线阵中，每个阵元不仅会收到自由空间中的直接入射波成分，同时也会收到互耦效应所导致的邻近阵元上的二次辐射分量。因此，各阵元的实际输出信号是空间中的直接入射波响应分量与邻近阵元耦合过来的寄生分量的叠加。这时，式（3）应修正为

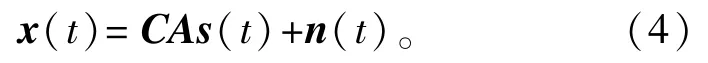
式中：C∈CCMN×MN代表互耦矩阵，矩阵中的元素表示了不同阵元间的耦合程度。针对简单的阵列配置，比如均匀线阵和圆阵，许多相关文献已经建立了对应的互耦模型［4-7］。而相比以上两种简单配置，平面阵涉及的互耦特征较为复杂，我们需关注的首要问题就是如何通过互耦矩阵C对其表征的互耦效应进行建模，下面给出一个完善的建模过程及模型描述。

如图1所示，均匀平面阵可看作是由N个沿x轴方向平行放置的直线阵所构成。因此，互耦效应不仅存在于每个子阵的阵元之间，而且也存在于不同子阵之间。根据均匀平面阵的对称结构以及互易原理，在一般意义上，互耦矩阵C可表示为

实际中，两阵元间的耦合强度会随着距离的增加迅速衰减，而相距较远的两阵元间互耦作用已不太明显，以至于可以忽略。基于这个事实，耦合向量cn中会存在一些零元素。对于均匀平面阵，我们考虑每个阵元最多与位于其四周第1，2，…，P-1个矩形网格上的阵元存在着耦合作用，而P＞2意味着阵元间存在着较强的互耦作用。为了避免空域混叠，假设横纵向的阵元间距均为半个波长，根据以上分析，此时的耦合向量cn可以记为

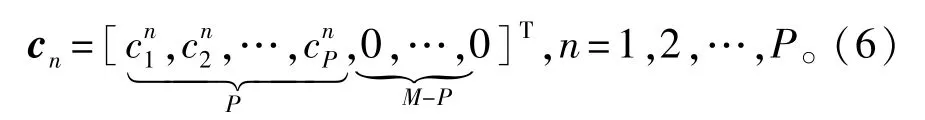
此时，阵列输出的协方差矩阵可以表示为

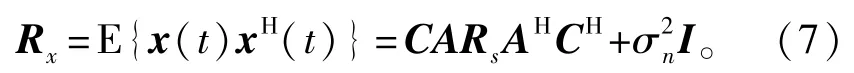
式中：上标H代表共轭转置；E｛·｝表示期望运算符；Rs=E｛s（t）sH（t）｝为信源协方差矩阵；而I是一个单位矩阵。考虑接收到L个可利用的阵列快拍｛x（t）｝Lt=1，由于这些阵列采样值均被互耦效应所扰乱，在此我们关心的问题是如何利用这些有限的阵列快拍估计出所有信源的二维方位｛θk，φk｝Kk=1，并同时估计出未知的互耦矩阵以据此进行互耦校正。

3　基于秩损估计的互耦自校正算法

当互耦矩阵C精确已知时，大部分传统的基于子空间原理的测向算法经过修正后均可有效地工作。基本地，只需要使用等效阵列响应CA来代替理想阵列响应A即可。因此，互耦矩阵已知时的测向问题与通常的情况并没有区别。然而，在互耦矩阵未知的情况下，上述方法便无法实施。在这一节中，我们将提出一种基于秩损原理的盲估计算法来解决这个问题。

3.1未知互耦效应下的2-D DOA盲估计

首先，我们仍基于广泛使用的子空间原理来展开讨论。通过对协方差矩阵Rx进行特征分解，我们将其中MN-K个较小特征值对应的特征向量所构成的矩阵记为En，而其余的特征向量所构成的矩阵被记为Es。由标准的子空间正交性可知，等效阵列响应CA与Es张成的信号子空间是相同的，并且与En所张成的噪声子空间是正交的，因此有

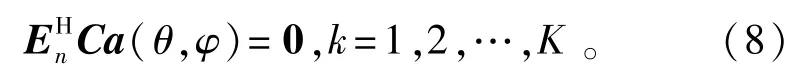
虽然上式中的C并不是精确已知的，但我们借助变换域处理，可巧妙地将二维DOA估计和互耦校正问题分离开。为此，首先需进行如下的参数变换：

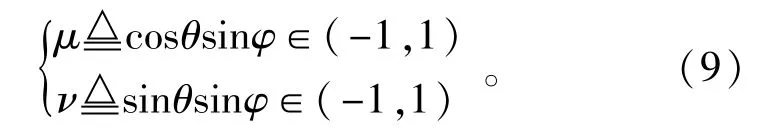
则式（2）给出的ax（θ，φ）和ay（θ，φ）可重新写为

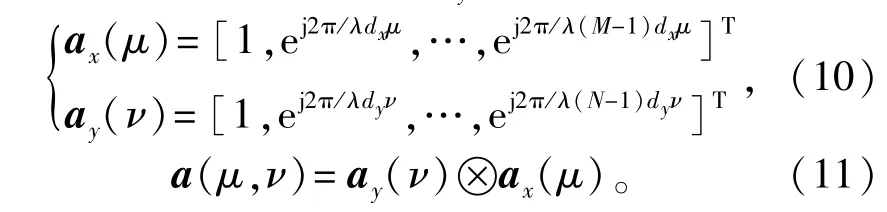
注意到当φ∈［0，π/2）时，参数对（μ，v）↔（θ，φ）之间存在着唯一的映射关系，因此成对的方位/俯仰角可以从（μ，v）域中无模糊地恢复出来，并且通过映射，我们还可在（μ，v）域实现数据的降维处理。在给出后续处理步骤之前先介绍如下的一个引理［4］。

引理1:对于任意一个M×M维的带状对称Toeplitz矩阵A以及M×1维的列向量x，如下的变换关系式是成立的：

式中：P×1维的列向量a由ai=A1i（i=1，2，…，P）给出；P为矩阵A的首行非零元素数目。而M×P维的矩阵Q（x）由如下两部分所构成：

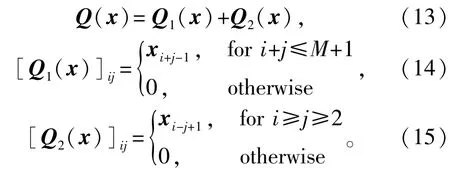
式中：［·］ij代表矩阵的第（i，j）个元素。

注意到式（5）中的互耦矩阵C具有分块对称的Toeplitz结构，因此等效导向矢量Ca（μ，v）可写为

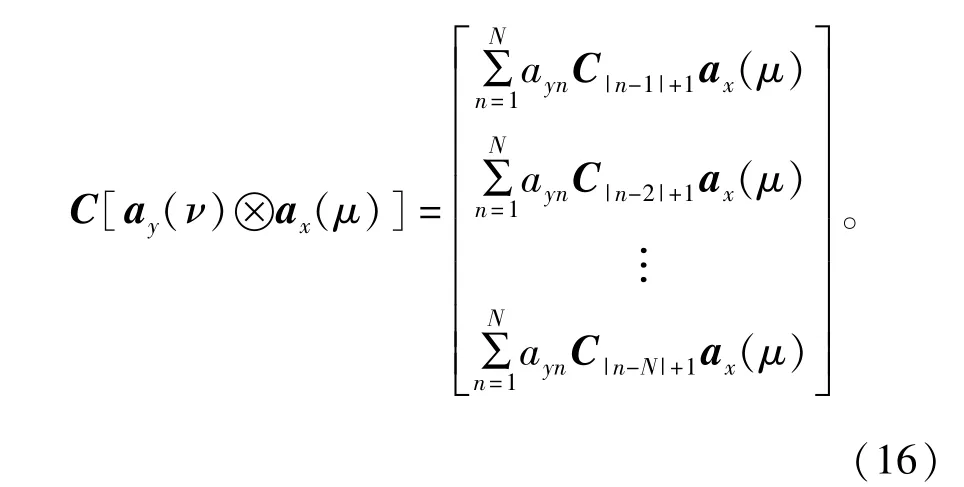
式中：ayn表示ay（v）的第n个元素。接下来，我们定义矢量，并运用引理1可得

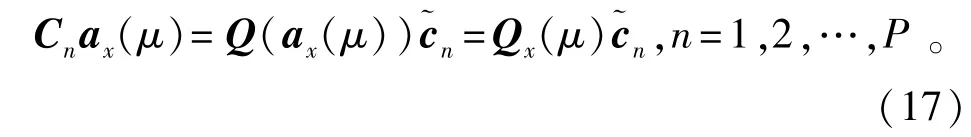
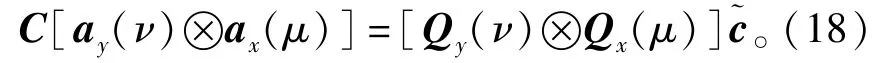
式中：矩阵Qy（v）∈CCN×P和Qx（μ）∈CCM×P具有相似的结构。注意到此时的向量包含了所有未知的互耦系数，并且阵列导向矢量仅在式（18）中进行了重新排列，涉及到了平面阵中的所有阵元，因此避免了阵列孔径损失。然后将式（18）代入到式（8）中，可得

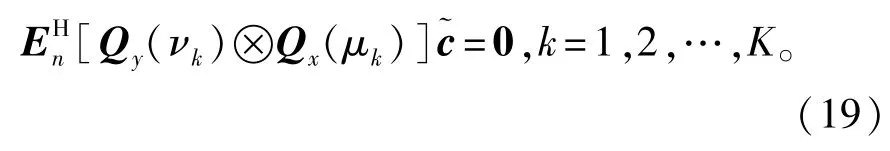
利用Kronecker积的性质，有

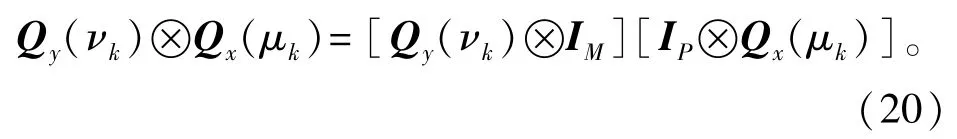
因此，式（19）可以重新写为

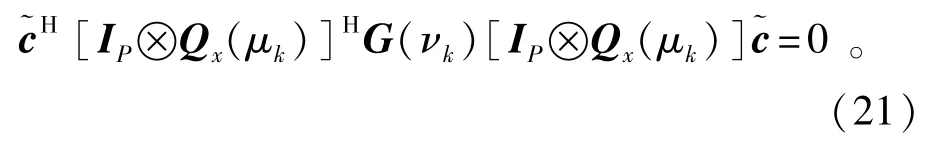
式中：G（vk）∈CCMP×MP定义为

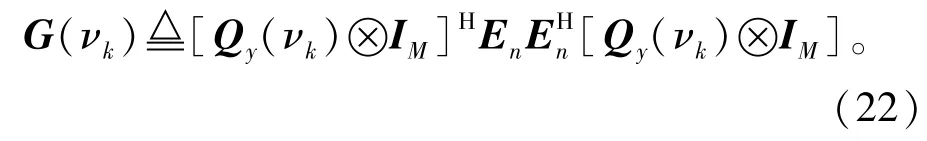
观察式（21），可以发现一个很重要的特征，即G（vk）是独立于互耦向量的，这使得我们可以借助秩损估计思想［9］，并将其扩展到二维场景下，以应用到上述问题的求解中。根据秩损估计原理，若秩损条件MN-K≥MP满足，那么一般情况下，矩阵G（v）是满秩的，因为此时矩阵En的列秩是不小于MP的。由于，则等式（21）仅在矩阵G（vk）缺秩的时候才成立，或者等价地当

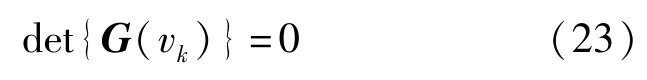
时才成立，其中det｛·｝代表矩阵行列式。

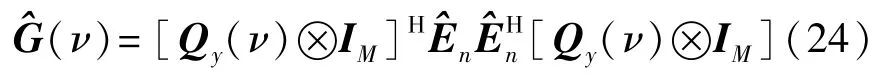
来代替G（v），并且上述G（vk）的秩损特性在渐进意义上是成立的，即当v的取值与真实值一致时，矩阵（v）的行列式才会取得一个最小值。因此，我们可以构造如下一个谱函数：

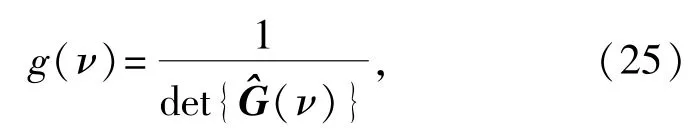
然后基于上式进行一维谱峰搜索，便可从函数g（v）的K个最高峰值处估计出所有的参量。

接下来，为了将秩损估计准则扩展到二维场景下，我们首先需定义一个P2×P2维矩阵，表示如下：

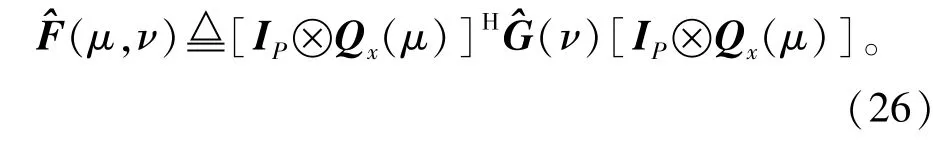
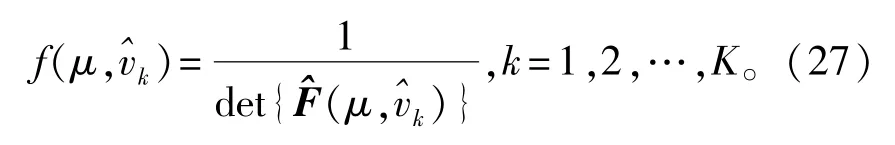
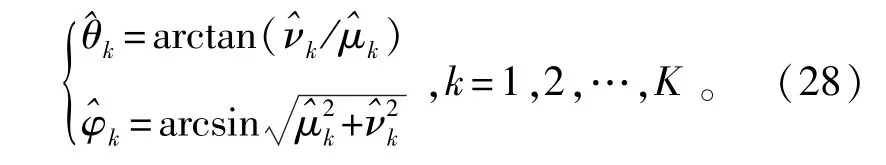
从这个角度来看，（μ，v）域上的谱峰搜索等价于（θ，φ）域上的谱峰搜索。然而需要强调的是，我们在所提出的算法中巧妙地利用了变换关系式（9）和式（28），这对简化整个解耦合方案是十分关键的。

3.2互耦系数估计

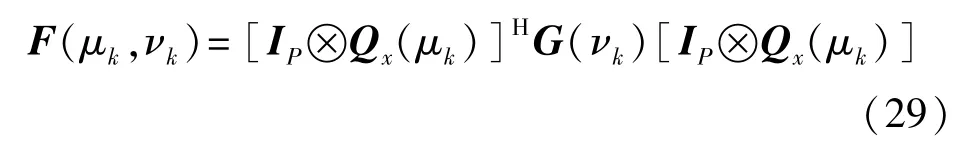
的零特征值所对应的特征向量。在秩损条件满足的情况下，可以证明矩阵F（μk，vk）是秩缺一的，这意味着对应于其零特征值的线性无关的特征向量仅有一个。因此，利用已估计出的所有参数组，我们可以构造如下一个解耦合矩阵：

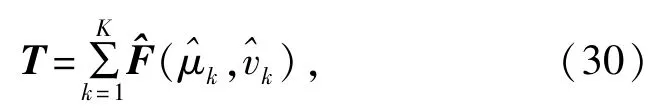
并将T的最小特征值对应的特征向量记为emin。由于互耦向量的第一个元素（即自耦项）取值为1，那么所有未知的耦合系数可以由

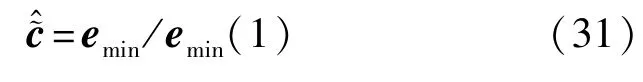
3.3算法复杂度分析

对于二维平面阵的互耦校正问题，基于子空间原理的谱搜索方法是目前的一个主要解决途径，而这类算法的计算复杂度主要由谱搜索过程中的运算量决定的。因此，我们通过统计在谱搜索过程中需要的复数乘法总数，将所提算法和文献［8］中辅助阵元法的计算复杂度进行一个对比。考虑以上两种算法均在（μ，v）域以同样的步长进行搜索，且每一维的搜索总点数记为n，那么辅助阵元法直接进行二维谱峰搜索时需要的复数乘法总数为

可见其复杂度随n呈平方级增长。由3.1节的内容可知，我们所提算法的搜索步骤分为两步：

综合以上两步操作，我们提出的算法在谱搜索运算过程中需要的复数乘法总数为n（PM3N2-PM2NK+M3P3）+nK（N2P4+P6），其复杂度随n是线性增长的。在高分辨率应用中通常需要进行精细的网格搜索以保证较高的估计精度，此时每一维的搜索点数是很大的，而所提算法由于使用了降维操作，避免了直接的二维搜索，使得计算效率大幅提升。

4　仿真结果与分析

在这一节中，我们将通过一系列的仿真实验来验证评估所提算法的性能。考虑空间中存在4个不相关的等功率信号源，对应的来波信号分别从（28°，41°）、（40°，20°）、（54°，66°）、（74°，35°）方向入射到平面阵上。假设平面阵中每个阵元仅和位于其四周的8个相邻阵元存在着耦合作用（即P=2），耦合系数向量设为且在n＞2时，有cn=0M×1。同时，上述仿真参数的设定和文献［8］也是保持一致的。我们将均方根误差（Root Mean Square Error，RMSE）作为指标来衡量算法的估计性能［8］。在后续仿真中，若无特别说明，接收的阵列快拍数均为500，蒙特卡洛仿真次数为1 000。

首先，我们在7×7维的平面阵规模下评估所提算法的测向性能。为了便于对比，文献［8］中的辅助阵元法也在等效的（μ，v）域中实现。图2给出了不同算法下2-D DOA估计的RMSE随信噪比（Signal-to-Noise Ratio，SNR）的变化曲线，其中还给出了估计误差的Cramér-Rao Bound（CRB）作为算法性能的衡量基准［8］。

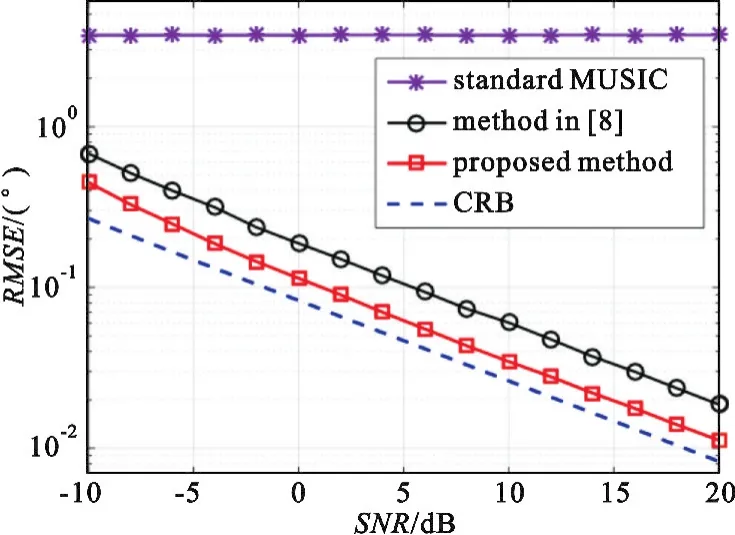
图2　2-D DOA估计的RMSE随SNR的变化曲线Fig.2 RMSE curves of DOA estimation versus SNR

由图2可看出，正如预期的，在未知互耦效应的影响下，标准的2-D MUSIC算法已经失效，此时即使增加信噪比，方位估计性能也没有改善，而前述两种自校正算法均可有效工作。不仅如此，我们所提算法的方位估计性能将更加接近CRB，在整个SNR观测区间均优于辅助阵元法约5 dB，初步证明了所提算法在方位估计性能上的优越性。

接下来，我们通过改变阵元总数来继续考察两种自校正算法在不同阵列规模下的估计性能。图3给出了当信噪比为5 dB时2-D DOA估计的RMSE随阵列规模（M=N）的变化曲线。如图所示，与现有的辅助阵元法相比，我们提出的算法在不同阵列规模下仍保持着较高的估计精度。注意到这两种自校正算法的性能差距会随着阵列规模的增大而缩小。这是容易解释的，因为当阵列规模增大时，辅助阵元法中涉及的阵列孔径损失会相对变小，因此导致了估计性能的有限程度退化。同样需强调的是，当阵列中存在较强的互耦效应时（即P＞2），辅助阵元法与所提算法间的性能差距会进一步扩大，因为前者将使用更多的辅助阵元，孔径损失随之增大。

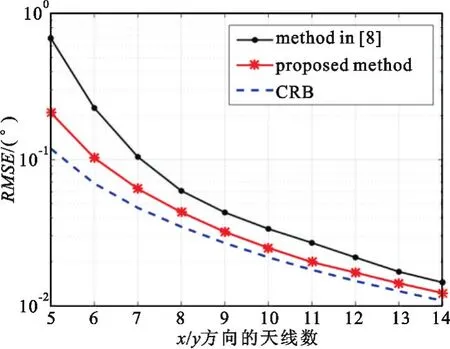
图3　2-D DOA估计的RMSE随天线数的变化曲线Fig.3 RMSE curves of DOA estimation versus the array size

最后，我们直接在14×14维较大的平面阵规模下，来对比评估这两种自校正算法的互耦估计性能。图4给出了互耦系数估计的相对RMSE随SNR的变化曲线。即使此时采用了较大规模的阵列，辅助阵元法的互耦估计精度仍然在较宽的低信噪比范围内明显低于我们所提的算法。类似的仿真现象在较小的阵列规模下也可观测到，这主要是由于辅助阵元法在估计互耦系数时采用的是最小二乘估计，而最小二乘法固有的估计精度在低信噪比下总是表现较差。此外，随着信噪比的进一步增加，可以发现以上两种算法的互耦估计性能均能渐进达到CRB。

图4　互耦估计的相对RMSE随SNR的变化曲线Fig.4 Relative RMSE curves of coupling estimation versus SNR

5　结论

本文针对均匀平面阵的二维测向问题，提出了一种基于秩损估计的互耦自校正算法。利用对互耦效应的先验知识，算法只需将受扰动的阵列响应在变换域中重新排列，便可避免传统算法由于阵列孔径损失所导致的估计精度降低问题。通过将秩损准则扩展到二维场景中，在变换域中设计了一种计算步骤，使得方位估计的降维操作得以实现，计算效率大大提升。并且，在估计互耦系数时采用了特征分解估计，低信噪比下的校正精度得到了明显的提升。

［1］KRIM H，VIBERG M.Two decades of array signal processing research：the parametric approach［J］.IEEE Signal Processing Magazine，1996，13（4）：67-94.

［2］谢鑫，程国标，路翠华.互耦效应对DOA估计的影响［J］.电讯技术，2010，50（7）：60-64.

XIE Xin，CHENG Guobiao，LU Cuihua.Impact of mutual coupling on direction of arrival estimation［J］.Telecommunication Engineering，2010，50（7）：60-64.（in Chinese）

［3］HENAULT S，ANTAR Y M M.Unifying the theory of mutual coupling compensation in antenna arrays［J］.IEEE Antennas and Propagation Magazine，2015，57（2）：104-122.

［4］SELLONE F，SERRA A.A novel online mutual coupling compensation algorithm for uniform and linear arrays［J］. IEEE Transactions on Signal Processing，2007，55（2）：560-573.

［5］WANG M，MA X，YAN S，et al.An auto-calibration algorithm for uniform circular array with unknown mutual coupling［J］.IEEE Antennas and Wireless Propagation Letters，2015，15（6）：12-15.

［6］LIN M，YANG L.Blind calibration and DOA estimation with uniform circular arrays in the presence of mutual coupling［J］.IEEE Antennas and Wireless Propagation Letters，2006，5（1）：315-318.

［7］LIAO B，ZHANG Z G，CHAN S C.DOA estimation and tracking of ULAs with mutual coupling［J］.IEEE Transactions on Aerospace and Electronic Systems，2012，48（1）：891-905.

［8］YE Z，LIU C.2-D DOA estimation in the presence of mutual coupling［J］.IEEE Transactions on Antennas and Propagation，2008，56（10）：3150-3158.

［9］SEE C M S，GERSHMAN A B.Direction-of-arrival estimation in partly calibrated subarray-based sensor arrays［J］.IEEE Transactions on Signal Processing，2004，52（2）：329-338.

刘 江（1968—），男，河北保定人，1989年于电子科技大学获图像传输与处理专业学士学位，现为高级工程师，主要从事航空电子系统技术和通用测试技术研究；

LIU Jiang was born in Baoding，Hebei Province，in 1968.He received the B.S.degree from University of Electronic Science and Technology of China in 1989.He is now a senior engineer.His research concerns avionics and general test technology.

Email：lj_6370@189.cn

张 辰（1990—），男，河南南阳人，2013年于西安电子科技大学获通信工程专业学士学位，现为硕士研究生，主要研究方向为阵列误差校正、多天线信号处理技术。

ZHANG Chen was born in Nanyang，Henan Province，in 1990.He received the B.S.degree from Xidian University in 2013.He is now a graduate student.His research concerns array error calibration and multi-antenna signal processing techniques.

2-D DOA Estimation and Mutual Coupling Self-calibration for Uniform Planar Arrays

LIU Jiang1，ZHANG Chen2
（1.Southwest China Institute of Electronic Technology，Chengdu 610036，China；
2.College of Information Science&Electronic Engineering，Zhejiang University，Hangzhou 310027，China）

For the robustness problem of direction finding algorithm using uniform planar arrays under mutual coupling，a rank reduction based self-calibration algorithm is proposed.Based on the priori knowledge of mutual coupling，the perturbed array response is just rearranged in the transform domain，thus being able to mask the adverse effect of mutual coupling，and avoid the aperture loss as well.Then according to the rank reduction criteria，the reduced-dimension processing is performed by applying suitably designed estimation procedure.Moreover，an accurate estimation of coupling coefficients can also be acquired for array calibration by eigen decomposition.Compared with the existing method，the proposed algorithm is more numerically efficient with improved accuracy.

uniform planar arrays；direction of arrival estimation；mutual coupling；self-calibration；rank reduction criteria

TN971

A

1001-893X（2016）04-0377-06

10.3969/j.issn.1001-893x.2016.04.005

刘江，张辰.均匀平面阵下的二维DOA估计与互耦自校正［J］.电讯技术，2016，56（4）：377-382.［LIU Jiang，ZHANG Chen.2-D DOA estimation and mutual coupling self-calibration for uniform planar arrays［J］.Telecommunication Engineering，2016，56（4）：377-382.］

2016-02-25；

2016-04-13 Received date:2016-02-25；Revised date:2016-04-13

**通信作者:lj_6370@189.cn Corresponding author：lj_6370@189.cn