不同河道形态岸坡抗冲刷能力的三维数值模拟分析
2016-11-01杨金林吴国宏王耀军闫长斌
杨金林, 吴国宏, 王耀军, 闫长斌
(1.黄河勘测规划设计有限公司,河南 郑州 450003; 2.郑州大学,河南 郑州 450001)
。
。
不同河道形态岸坡抗冲刷能力的三维数值模拟分析
杨金林, 吴国宏, 王耀军, 闫长斌
(1.黄河勘测规划设计有限公司,河南 郑州 450003; 2.郑州大学,河南 郑州 450001)
为了研究不同河道形态岸坡的抗冲刷问题,采用轴比λ定义了不同河道形态岸坡:当λ=0时,岸坡坡面形状为平面形;当λ=1/5、1/4、1/3、1/2时,岸坡坡面形状为椭圆形;当λ=1时,岸坡坡面形状为圆形。利用数值软件分析了不同形状岸坡坡角α、坡高h与岸坡抗冲刷能力F之间的关系。结果表明:①对平面形岸坡形状:当h不变时,岸坡抗冲刷能力F随岸坡坡角α的增大而呈现递减变化;当坡角α不变时,抗冲刷能力F随坡高h的增大而呈现递减变化。②对凹形岸坡形状(椭圆形、圆形):当λ、h不变时,岸坡抗冲刷能力F随坡角α的增大而呈现递减变化;当α、h不变时,岸坡抗冲刷能力F随轴比λ的增大呈现先增大后减小的变化。此分析结果可为小浪底库区岸坡形状优化提供参考。
河道形态;抗冲刷能力;数值模拟;小浪底水库
随着部分地区遭受强降雨连袭以及库水位的变化,小浪底库区垣曲段(沇河、亳清河两岸)黄土岸坡受河水冲刷出现较为严重的塌岸,通过对塌岸区岸坡调查发现,不同形态岸坡塌岸与河道形态有着密切的关系,如河道弯曲度、岸坡坡角、坡高等。为了研究不同形态岸坡的抗冲刷能力,一些学者采用理论计算和数值模拟的方法对岸坡的稳定性问题进行了探讨,如朱乃龙等基于弹性力学理论,分析了椭圆形岸坡上任意点的临界稳定坡角和岸坡的力学效应,优化了不同形态岸坡的形状[1-2];盛建龙基于弹性力学和热力学理论,计算出了岸坡合理的坡角,并得出了最佳岸坡形状[3];杨坤等运用确定性和不确定方法对块状结构岩体进行了稳定性分析[4];姜彤等研究了抗剪强度c、φ值对岸坡稳定性的影响[5];刘娉慧等基于强度折减法分析了岸坡的稳定性问题[6]。
在借鉴上述文献研究思想的基础上,笔者基于强度折减法理论,运用有限元数值分析软件,对河道不同的弯曲度、岸坡坡角、坡高及其抗冲刷能力之间的关系进行了研究,得到了一些研究成果。这些成果可为优化小浪底库区黄土岸坡形状提供参考。
1 计算原理与方法
1.1 计算原理
用强度折减有限元法[6-9]分析岸坡的稳定性,采用解的不收敛作为破坏标准[10],在指定的收敛准则下算法不能收敛即表示应力分布不能满足岩体的破坏准则和总体平衡要求,意味着岸坡达到临界失稳状态[11]。
岸坡安全系数为沿滑动面的抗剪强度与滑动面的实际剪应力的比值,其公式可表示为:
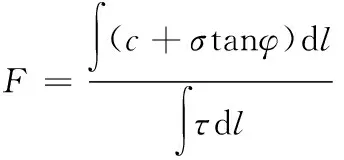
将上式等号两边同时除以F,得
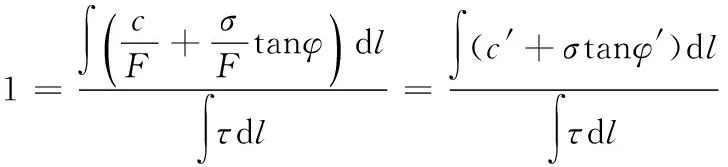
其中
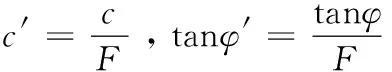
式中:F为安全系数;c为岩土黏聚力;为岩土内摩擦角;为滑动面上正应力;为滑动面剪应力。
通过逐步调整试验中的F值,可得到不同的c′、φ′,将c′、φ′代入模拟计算程序,反复折减,直到岸坡达到临界状态,临界状态的F值即是岸坡的安全系数。
1.2 岸坡形态
采用轴比λ(λ=a/b)定义不同河道形态岸坡,a代表垂直河流方向尺寸,b代表河流方向尺寸,轴比越大,河流的弯曲度越大。当λ=0时,河流无弯曲度,岸坡形状为平面形;当λ=1/5、1/4、1/3、1/2时,岸坡坡面形状为椭圆形;当λ=1时岸坡坡面形状为圆形,如图1所示。岸坡纵向剖面如图2所示。

图1 不同河道形态岸坡划分示意图

图2 岸坡纵向剖面示意图
1.3 模拟假定
假定在同等水力冲刷条件下,岸坡的抗冲刷能力以安全系数的大小来反映,即同等条件下,不同河道形态岸坡的安全系数值越大,认为该形态岸坡的抗冲刷能力越强。基于这种思想,以岸坡的安全系数值代表岸坡的抗冲刷能力,用轴比反映河道弯曲度,用不同坡角反映河道的空间形态。
1.4 岩土体物理力学指标
为确定模拟岸坡的岩土体物理力学性质,取岩土样进行了室内物理力学试验,并选出以下岩土体物理力学指标值,具体见表2。

表2 岩土体物理力学指标值
1.5 计算工况
分别讨论岸坡坡高h=10、20、30、40、50 m,岸坡坡角α=15°、30°、45°、60°、75°、90°,河道轴比λ=0、1/2、1/3、1/4、1/5时,三者与抗冲刷能力之间的关系。模型四周及底部采用位移约束,岸坡初始应力按自重应力考虑,假定岩土体为均质同性体。
2 结果分析
2.1 平面形岸坡
当λ=0时,岸坡坡面形状为平面形,分别改变坡角α(15°、30°、45°、60°、75°、90°)、坡高h(10、20、30、40、50 m)的数值,得到坡角α、坡高h与抗冲刷能力F之间的关系,如图3所示。
从图3中可以看出:
1)当α不变时,抗冲刷能力F与坡高h成反比关系,h越大,岸坡的抗冲刷能力越小。抗冲刷能力在h=20 m时的增幅趋势跳跃比较大;当h=30、40、50 m时,岸坡的抗冲刷能力受坡高的影响较小,岸坡的抗冲刷能力在坡高h=10、20 m时增加的速率明显高于坡高h=30、40、50 m时的;坡角相同,当水库临库岸坡坡高达到极限坡高之前,坡高是影响岸坡失稳的一个主要因素。
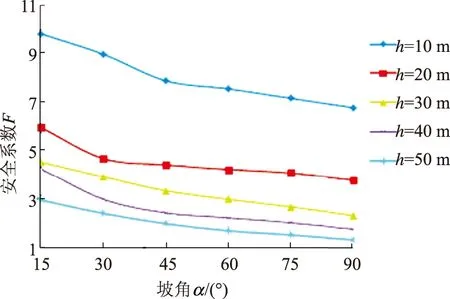
图3 平面形坡面α、h与F的关系曲线
2)当h不变时,岸坡的抗冲刷能力F与坡角α成反比:当α≤45°时为第一阶段,当45°<α≤90°时为第二阶段。当α=15°时,抗冲刷能力最强,随着坡角继续增大,抗冲刷能力逐渐减小;第一阶段抗冲刷能力减小速率较第二阶段抗冲刷能力减小速率大;第二阶段抗冲刷能力F随着坡角α的增大而变小的速率减缓,当坡角α=90°时,岸坡抗冲刷能力达到最小值。
2.2 凹面形岸坡
当坡面形状为凹面形时,即椭圆形坡面或圆形坡面时,分别改变坡角α(15°、30°、45°、60°、75°、90°)、坡高h(10、20、30、40、50 m)和轴比λ(1/5、1/4、1/3、1/2、1)的值,模拟得到坡高h、坡角α、轴比λ与抗冲刷能力F之间的关系,如图4—14所示。
由图4—8可知:
1)当h不变时,抗冲刷能力F与轴比λ呈非线性关系,即抗冲刷能力F随着轴比λ的增加呈现先增加后减小的规律。当λ>1/3时,抗冲刷能力F随着轴比λ的增大呈现减小的趋势;当轴比λ≤1/3时,抗冲刷能力F随着轴比λ的增大呈现增加的趋势。

图4 h=10 m时F与λ、α的关系曲线
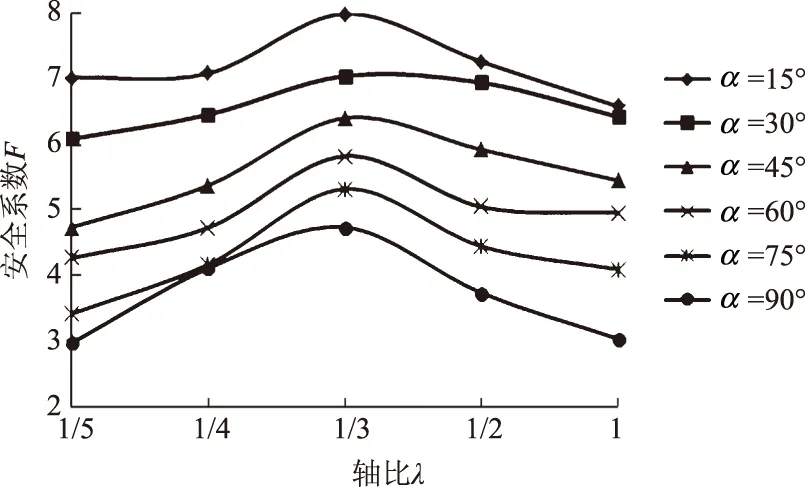
图5 h=20 m时F与λ、α的关系曲线
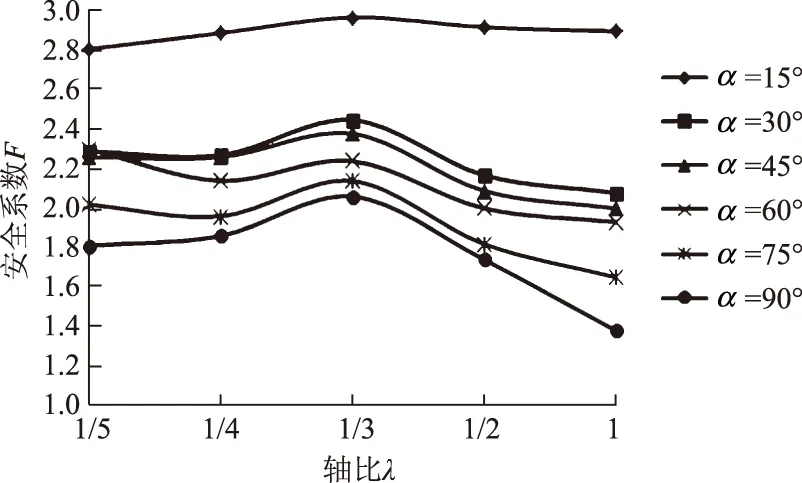
图6 h=30 m时F与λ、α的关系曲线
2)凹面形岸坡的抗冲刷能力F与坡角α成反比关系,出现的规律和平面形岸坡的规律类似。当α≥30°时,岸坡抗冲刷能力增加速率较缓;当α=90°时,岸坡的抗冲刷能力变化频率较快。原因主要是岸坡的破坏模式从压剪破坏转变为拉剪破坏。

图7 h=40 m时F与λ、α的关系曲线
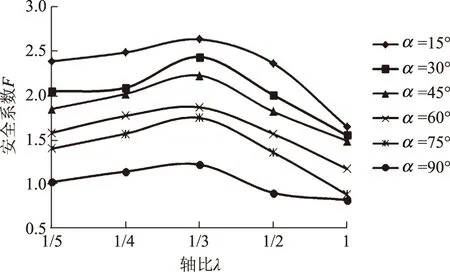
图8 h=50 m时F与λ、α的关系曲线
由图9—14可知:当α不变时,岸坡的抗冲刷能力F随着坡高h的增加快速减小。当坡角α不变时、坡高h<30 m时,岸坡的抗冲刷能力随着坡高的增加而减小;当h>30 m时,岸坡的抗冲刷能力减小得较慢。总体来说,岸坡的抗冲刷能力随着岸坡坡高的增加而减小,坡高越高,安全系数越小,当坡高达到一定值时,岸坡局部某一面逐渐接近于临界状态,即出现极限平衡状态。
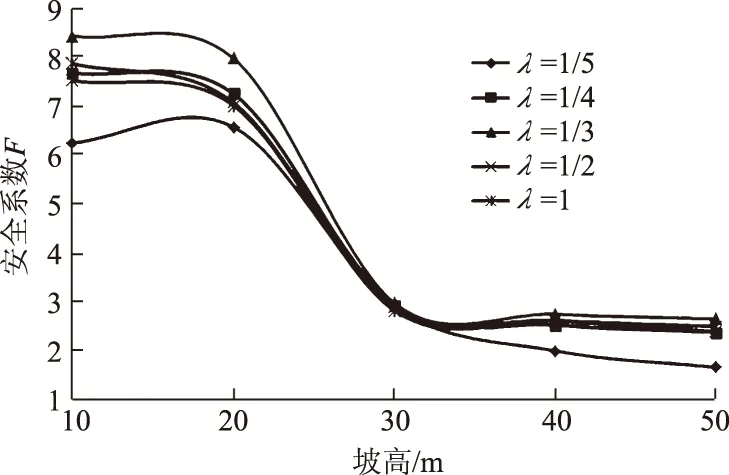
图9 α=15°时F与h、λ的关系曲线
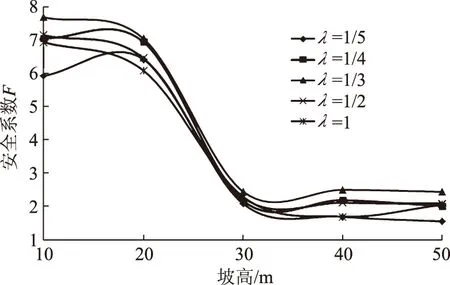
图10 α=30°时F与h、λ的关系曲线
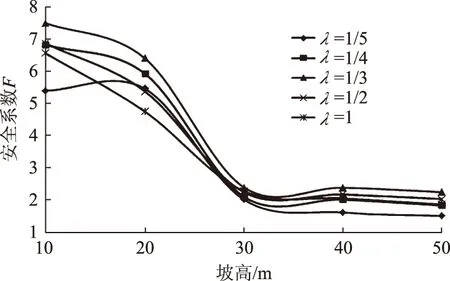
图11 α=45°时F与h、λ的关系曲线
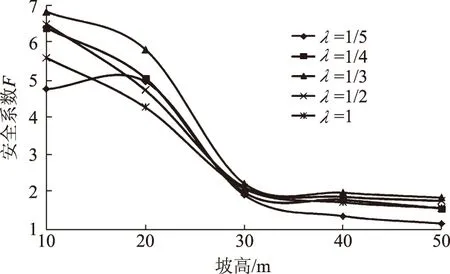
图12 α=60°时F与h、λ的关系曲线

图13 α=75°时F与h、λ的关系曲线
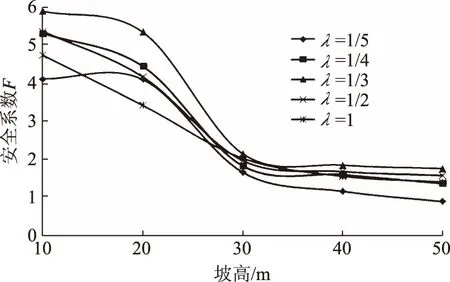
图14 α=90°时F与h、λ的关系曲线
3 结 语
1)利用轴比λ定义了不同河道形态岸坡,将岸坡的形状分为平面形、椭圆形和圆形3种。
2)岸坡形状为平面形时,当坡角α不变时,岸坡的抗冲刷能力F随着坡高h的增加呈现减小的趋势,随着坡高h的增加,岸坡抗冲刷能力F增速减缓。
3)当坡高h不变时,岸坡的抗冲刷能力F随坡
角α增加而减小,当坡角α≥30°时,抗冲刷能力F减小速率减缓,当α=90°时,抗冲刷能力F达到最小值。
4)对于凹面形岸坡,当轴比λ≤1/3时,岸坡抗冲刷能力F随着轴比λ的增大出现增加的趋势;当λ>1/3时,抗冲刷能力随着轴比的增大而减小;当轴比λ=1/3时,河道岸坡抗冲刷能力相比于其他弯曲度岸坡的抗冲刷能力强。
5)文中基于有限元法,在假定岩土体为各向同性体的基础上,对岸坡抗冲刷能力与河道弯曲度、岸坡坡角、坡高之间的关系进行了模拟分析,得出了一些结论。但文中仅用岸坡安全系数反映岸坡抗冲刷能力存在不足之处,有待进一步研究完善。
[1]朱乃龙,张世雄.椭圆形深凹露天矿稳定性边坡形状确定方法的研究[J].岩石力学与工程学报,2004,23(4):603-606.
[2]朱乃龙,张世雄.深凹露天矿边坡稳定的空间受力状态分析[J].岩石力学与工程学报,2003,22(5):810-812.
[3]盛建龙.最佳边坡形状的力学分析及应用研究[J].力学与实践,2002,24(4):38-42.
[4]杨坤,于冬梅,阎雪莲,等.岩石边坡块状结构岩体稳定分析和可靠性评价[J].华北水利水电学院学报,2004,25(3):54-57,61.
[5]姜彤,马莎,李永新.抗剪强度c、φ值概率分布对边坡可靠性分析的影响[J].华北水利水电学院学报,2004,25(3):46-49.
[6]刘娉慧,房后国,黄志全,等.FLAC强度折减法在边坡稳定性分析中的应用[J].华北水利水电学院学报,2007,28(5):52-54,58.
[7]MANZARI M T,NOUR M A.Significance of soil dilatancy in slope stability analysis[J].Journal of Geotechnical and Geoenvironmental Engineering SCE,2000,126(1):75-80.
[8]DAWSON E M,ROTH W H,DRESCHER A.Slope stability analysis by strength reduction[J].Geotechnique,1999,49(6):835-840.
[9]GRIFFITHS D A,LANE P A.Slope stability analysis by finite elements[J].Geotechnique,1999,49(3): 387-403.
[10]连镇营,韩国城,孔宪京.强度折减有限元法研究开挖边坡的稳定性[J].岩土工程学报,2001,23(4):407-411.
[11]林杭,曹平,李江腾,等.边坡临界失稳状态的判定标准[J].煤炭学报,2008,29(6):643-647.
(责任编辑:杜明侠)
Three-dimension Numerical Simulation Analysis on the Anti-erosion Capacity of Slopes with Different Geometric Properties of River across Section
YANG Jinlin1,WU Guohong1,WANG Yaojun1,YAN Changbin2
(1.Yellow River Engineering Consulting Co., Ltd., Zhengzhou 450003,China; 2.Zhengzhou University, Zhengzhou 450001,China)
In order to investigate the anti-erosion capacity of bank slopes with different geometric properties of river across section, the bank slopes with different geometric properties of river across section were defined based on the axial ratioλ: The slope shape was plane whenλ=0, the slope shape was elliptical whenλ=1/5, 1/4, 1/3, 1/2, and the slope shape was rounded whenλ=1. The relationships among the slope angleα, the slope heighthand the anti-erosion capacityFof different slope shapes were analyzed with numerical simulation software. The results shows that: ① For the plane slopes, the anti-erosion capacityFdecreases while the slope angleαincreases under the conditions of not changing the slope heighth, the anti-erosion capacityFdecreases while the slope height hincreases under the conditions of not changing the slope angleα. ② For the concave slope shapes (elliptical shapes and rounded shapes), the anti-erosion capacityFdecreases while the slope angleαincreases under the conditions of not changing the axial ratioλand the slope heighth, the anti-erosion capacityFincreases firstly and then decreases when the axial ratioλincreases under the conditions of not changing the slope angleαand the slope heighth. These results can provide some
for optimizing the slope shape of Xiaolangdi Reservoir Area.
geometric properties of river across section; anti-erosion capacity; numerical simulation; Xiaolangdi Reservoir
2016-02-29
国家自然科学基金项目(U1504523);黄河勘测规划设计有限公司自主研究开发项目(2012-ky18)。
杨金林(1984—),男,河南商丘人,工程师,硕士,主要从事工程地质勘察、设计方面的研究。E-mail:yangjl@yrec.cn。
10.3969/j.issn.1002-5634.2016.03.012
TV148
A
1002-5634(2016)03-0060-05
