基于粒子群算法的太子河水量优化调度研究
2016-11-01徐建新吕爽樊华
徐建新, 吕爽, 樊华
(华北水利水电大学,河南 郑州 450045)
Xim=Xim+Vim。
。
基于粒子群算法的太子河水量优化调度研究
徐建新, 吕爽, 樊华
(华北水利水电大学,河南 郑州 450045)
基于粒子群算法,构建了太子河水量优化调度模型,用于解决太子河水量优化调度的问题。应用结果表明,通过采用该模型对观音阁与葠窝两座水库的库容进行优化,提高了两座水库分别对本溪市与辽阳市的总供水量,由调度前的83 131 万m3增加至101 052 万m3,两市综合供水保证率提高了17.1%,解决了两市综合供水保证率低的问题。运用该方法可有效地提高太子河水量优化调度问题的执行效率,计算结果合理可行,具有较高的灵活性和广泛的应用前景。
水量优化调度;粒子群算法;太子河流域
太子河位于东经122°26′—124°53′,北纬40°29′—41°39′,是大辽河左侧的一条支流,其发源于辽宁省新宾县,河长413 km,流域面积13 884 km2(属辽宁省水资源),流经本溪市和辽阳市,与浑河汇流形成大辽河。太子河上游的两座大型水利工程——观音阁水库和葠窝水库,在保证本溪市和辽阳市的生活、农业和工业用水等方面发挥了重要作用。近年来,水库的截流作用使得下泄流量明显减少,这对下游河段的生态环境造成了一定的负面影响。随着社会经济的发展和人们对生态环境的重视,太子河流域内的社会经济用水与生态环境用水的矛盾日趋明显。因此,如何进行水量优化调度已成为该流域亟待解决的关键问题。
水库水量优化调度是以运筹学为理论基础,构建以水库为中心的目标函数[1],设定约束条件,再以最优化方法结合现代计算技术求解系统方程组,从而得到满足调度原则的水库水量优化调度方案。太子河水量优化调度则是在保证流域内最小生态流量的前提下,将多个水源的水量更加合理地分配给多个用户,从而使系统的总缺水率最小[2]。采用一般方法如动态规划法[3]、穷举法、遗传算法[4]等求解该问题时会很复杂,且当用户数量及用水量的取值数目增多时,计算量也会增大,甚至出现“维数灾”的现象[5],因而很难应用于实际工作中。而粒子群算法是随机全局优化算法,需要调整的参数不多,构造简单,容易实现,有较强的寻优功能和通用性。于是,本文采用粒子群算法构建太子河流域内水量优化调度模型,进行系统优化求解。
1 基于粒子群算法的水库水量优化调度模型
1.1 粒子群算法原理
1995年,Kennedy和Eberhart[6]创造性地提出了粒子群算法(Particle Swarm Optimization,PSO)。它是一种群智能算法,源于Reynolds对鸟群觅食行为的灵感,即通过个体间的竞争与协作完成全局搜索。在粒子群算法中,若将一个待优化的问题看成是一群鸟在空中寻觅一块食物,那么每一只觅食的鸟都是粒子群算法中搜索最优解的一个粒子,它们根据所有鸟的飞行经验来不断调整自己以后的飞行方式。个体极值[7]是每一个粒子所经历的最佳位置,也就是该粒子当前寻找到的最优解。同样,全局极值[8]是全体粒子所经历的最佳位置,也就是整个群体当前寻找到的最优解。寻得最佳位置的每个粒子经过上述两个极值后,以式(1)、(2)来不断更新自己的速度和位置,进而产生新一代群体。由此可知,每个粒子都是跟随目前的最佳粒子在解的空间里不断搜索。
Vim= ωVim+c1r(pB[i]-Xim)+
c2R(pB[g]-Xim),
(1)
Xim=Xim+Vim。
(2)
式中:Vim为迭代粒子i在第m维搜索空间中的前进速度;ω为惯性权重;c1、c2为常数,被称为学习因子;r、R为[0,1]均匀分布上的随机数[8];pB[i]为粒子i在第m维搜索空间里的个体极值所在位置;pB[g]为整个粒子群体在第m维搜索空间里的全局极值所在位置;Xim为迭代粒子i在第m维搜索空间中的当前位置。
在式(1)中,ωVim是粒子之前的速度,说明了当前的粒子状态,显示了平衡局部搜索和全局搜索的功能;c1r(pB[i]-Xim)是粒子认知结构,表明了粒子自身的思考,这就会避免粒子出现局部极小,同时有了较强的全局搜索能力;c2R(pB[g]-Xim)是带有社会属性的结构,体现了粒子之间的信息共享。只有在这3个部分的共同影响下,粒子才能更加迅速地到达全局最优位置。此外,粒子在根据速度不断地调整自己的位置时,还要受到最大速度Vmax的约束,当Vi达到或超过Vmax时将被赋值为Vmax。
1.2 水库水量优化调度模型
水库水量优化调度的核心就是要科学协调生产,兼顾生活、农业、工业和生态用水需求。以生活、农业、工业与生态环境用水的最大保证率为目标,重新对水量进行合理分配。
1.2.1 目标函数
追求缺水量最小,采用生活、农业、生态和工业用水保证率最大化来实现水资源利用目标,即
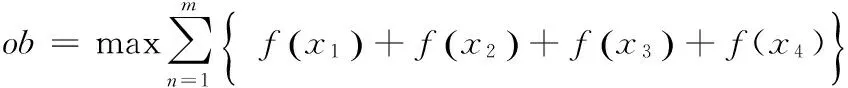
(3)
式中:m为水库个数;x1、x2、x3、x4依次为生活、农业、生态和工业用水保证率。
1.2.2 约束条件
1)生态流量约束。保证河道生态水量大于最小生态流量。
2)水库节点水量平衡约束。水库节点水量平衡关系如图1所示。i节点的流量等于i-1节点流量、节点之间支流来水量、两节点之间的退水水量之和,再减去两节点之间的实际用水量和两节点之间的损失水量。
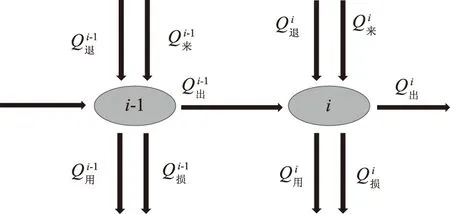
图1 水库节点示意图
3)水库水量平衡约束。某时段末的蓄水量为该时段初的蓄水量与时段入库水量之和,再减去该时段水库损失水量(包括蒸发水量和渗漏水量)。
4)水库水位过程约束。保证水库水位在死水位和防洪限制水位之间。
5)出库流量约束。要求出库流量大于最小下泄流量,且小于最大下泄流量。
6)其他约束。变量均为非负约束。
1.3 模型求解
实现水量优化调度就是要找到一个水位变化序列(X1,X2,…,Xn)[6],使其在满足所有的约束条件下实现目标函数。用粒子群算法对模型求解时,一个粒子就代表着一种水库运行策略,各时段末水库水位就是每个粒子的位置向量元素,各时段末水库水位的涨落速度就是速度向量元素,同时各时段末水库水位的变化值必须满足上述模型中的5个约束条件。具体步骤如下:
步骤1 确定粒子群规模n、空间维数m、最大迭代次数以及PSO算法基本参数。

步骤3 按照式(3)计算出各粒子的目标函数值,若优于当前粒子的E(i),就将Pi设置为此粒子的位置,同时更新E(i);若所有E(i)中有优于当前的Eg,则将Pi设置为此粒子的位置,同时更新Eg。
步骤4 按照式(1)、(2)更新每个粒子的位置与速度。
步骤5 检验计算结果是否达到最小误差要求和当前迭代次数是否达到了设定的迭代最大次数,若是满足以上条件之一,那么迭代终止;若不满足,继而转到步骤3,继续迭代。
当迭代终止时,系统记录下的全局极值位置点即为水库的目标调度曲线。
2 实例分析
2.1 数据来源
观音阁水库和葠窝水库坐落于太子河上游,是太子河干流上的两座大型水利工程。观音阁水库面积为61 km2,汇水面积2 795 km2;葠窝水库面积为39.9 km2,汇水面积3 380 km2,两座水库特征水位见表1,相对应的特征库容见表2。各水库区间的来水、河道外生活与工业需水量均采用本溪与辽阳站2006年的实测数据,农业需水量则采用多年平均值。本溪和辽阳断面生态需水量分别为396万m3和363万m3;太子河干流在频率为25%、50%、75%时的年际降水量依次为863.37、738.55、647.73 mm。

表1 观音阁与葠窝水库特征水位 m

表2 观音阁与葠窝水库特征库容 106m3
2.2 计算与结果分析
本次调度期选取为一日历年,算法用MATLAB语言编程实现,将每时段水库水位离散成500个状态,权重值取ω=0.729 8,c1=c2=1.494 45[9]。
通过采用粒子群算法对太子河干流水量进行优化调度,得到2006年两个水库的优化水位变化曲线,再根据水位与库容的相关关系得到两座水库的库容变化曲线,如图2所示。图中以每月1日、11日、21日为监测时间点。

图2 2006年观音阁与葠窝水库调度前后库容变化曲线
从图2中可以看出:1—4月以及11—12月,调度后的观音阁水库库容大于实际库容;5—10月,调度后的观音阁水库库容小于实际库容;1月及9—12月,调度后的葠窝水库库容大于实际库容;2—8月,调度后的葠窝水库库容小于实际库容。即实施调度后,冰冻期内观音阁水库和葠窝水库分别为本溪市与辽阳市提供工业用水的同时将所有来水存蓄,导致水库库容增加,待到4月中旬农耕开始,逐渐提高供水量,水库库容随之降低。
观音阁水库和葠窝水库调度前后本溪市与辽阳市供水量比较见表3。由表可知:本溪市和辽阳市的供水量调度后比调度前分别增加了9 040万m3和8 880万m3;两市的平均供水保证率分别提高了21.3%和14.1%,调度后两市的综合供水保证率为96.1%,相较于调度前提高了17.1%。调度后供水量的大幅度提高,可改善两市居民的生活舒适度并促进地区企业的可持续发展。
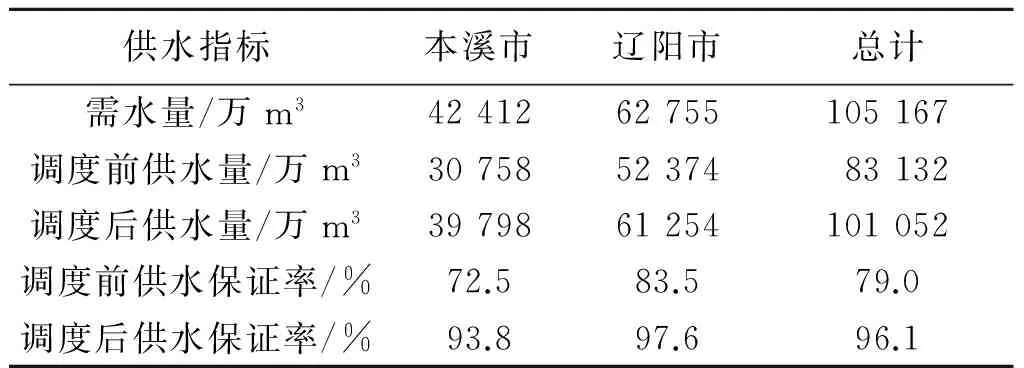
表3 水库调度前后本溪市与辽阳市供水特征比较
2.3 结果合理性分析
通过对数据资料验证与分析,本文计算结果合理,调度方案可行。
1)调度前,观音阁水库可为本溪市提供工业、生活及生态用水。实施调度后,由于1—4月以及11—12月不属于作物需水期,可不考虑农业用水。因此观音阁水库在保证本溪市充足的工业与生活用水的同时,可以适当减少水库下泄流量,故该时段调度后观音阁水库库容高于调度前库容。自5月起,生态与农业需水量逐渐增加,由于观音阁水库本身并没有直接供给农业用水,故调度后的观音阁水库适当增加了生态供水量,生态退水又用于农业灌溉,既提高了水资源利用效率,又缓解了农业用水需求。同时为保证水库及其下游的安全,汛期内的水库库容应处于汛限水位相应库容以下,故5—10月调度后的观音阁水库库容小于调度前的库容。
2)葠窝水库可为辽阳市提供生活、农业和工业用水。葠窝水库原本就未提供环境用水,而实施调度后,自2月中旬起,葠窝水库将为辽阳市增加提供环境用水,又随着农耕开始,辽阳市的综合用水量相继增加,则葠窝水库库容逐渐减少;至8月末,农业供水量减少,水库库容会逐渐增加。为保证水库及其下游安全,汛期时水库库容应在汛限水位相应库容以下。整个调度时期在满足所有约束条件下,提高了辽阳市的生活、农业、工业与生态用水保证率。
3 结 语
1)应用粒子群算法,构建了太子河水量优化调度模型,实现了太子河水量的重新分配。观音阁水库可供水量增加了9 040万m3,葠窝水库可供水量提高了8 880万m3。本溪与辽阳两市的综合供水保证率达到了96.1%,相较于调度前增加了17.1%。本文计算结果合理,调度方案可行,可为缓解太子河上游水资源供需矛盾,维护太子河水事秩序的稳定性以及促进当地经济社会的和谐稳定与可持续发展提供重要保障。
2)应用实例表明,粒子群算法有较强全局搜索最优的能力,且结构简单,计算速度快,结果合理可行,适用于水库水量的优化调度研究与分析。
[1]王本德,周惠成,卢迪.我国水库(群)调度理论方法研究应用现状与展望[J].水利学报,2016,47(3):337-345.
[2]陈南祥,刘为,高志鹏,等.基于多目标遗传-蚁群算法的中牟县水资源、优化配置[J].华北水利水电大学学报(自然科学版),2015,36(6):1-5.
[3]CHENG Chuntian,WANG Sen,CHAU Kwok-Wing,et al.Parallel discrete differential dynamic programming for multireservoir operation[J].Environmental Modelling & Software,2014(57):152-164.
[4]马黎,冶运涛.梯级水库群联合优化调度算法研究综述[J].人民黄河,2015,37(9):126-132,139.
[5]郭生练,陈炯宏,刘攀,等.水库群联合优化调度研究进展与展望[J].水科学进展,2010,21(4):496-503.
[6]KENNEDY J,EBERHARB R C.Particle swarm optimization[C]∥Proceedings of the IEEE international conference on neural networks.Piscataway NJ:IEEE Service Center,1995:1942-1948.
[7]徐鹤鸣.多目标粒子群优化算法的研究[D].上海:上海交通大学,2013:17-19.
[8]张水平,王碧.动态搜索空间的粒子群算法[J].计算机应用研究,2016,33(7):1-6.
[9]陈欢.粒子群优化算法在水电站水库优化调度中的应用研究[D].安徽:合肥工业大学,2010:36-37.
(责任编辑:张陵)
Investigation on Optimal Water Dispatching of Taizi River Based on Particle Swarm Algorithm
XU Jianxin, LV Shuang, FAN Hua
(North China University of Water Resources and Electric Power, Zhengzhou 450045,China)
For resolving the optimal water dispatching of Taizi River, the optimal water dispatching model of Taizi River was built based on Particle Swarm Optimization (PSO) Algorithm. The applied results show that using the model, the storage of Guanyinge Reservoir and Shenwo Reservoir is optimized, the total water supply of Benxi City and Liaoyang City from the two reservoirs increases, the water supply increases to 101 052 ×104m3from 83 131×104m3before dispatching, the integrated water supply guarantee rate of two cities increases by 17.1%, the low water supply guarantee rate of two cities is improved, the execution efficiency of optimal water dispatching of Taizi River effectively increases after utilizing the method, and the results are reasonable and feasible, and the method has higher flexibility and wider implementation prospect.
optimal water dispatching;Particle Swarm Optimization Algorithm; Taizi River Basin
2016-04-11
甘肃省科技支撑计划项目(144NKCD238)。
徐建新(1954—),男,吉林长春人,教授,博士,主要从事区域水资源高效利用管理理论与方法的研究。E-mail:xujianxin@ncwu.edu.cn。
10.3969/j.issn.1002-5634.2016.03.006
TV213.4
A
1002-5634(2016)03-0032-04
