带权重分数阶积分图像去噪方法

娄联堂,方自成,韦茜妤,吴高林

(中南民族大学 数学与统计学学院，武汉 430074)



带权重分数阶积分图像去噪方法

娄联堂,方自成*,韦茜妤,吴高林

(中南民族大学 数学与统计学学院，武汉 430074)

为了在图像去噪的同时保留更多图像的细节信息，在Riemann-Liouville定义的分数阶积分基础上，在数字信号的近似过程中引入权重参数，提出了一种通过调节权重与积分阶次并结合8个方向上的掩膜进行图像去噪的方法．实验结果表明：与传统去噪方法相比较，该方法不仅可以提高图像的峰值信噪比，而且还可以更好地保留图像纹理细节信息．

权重；分数阶积分；图像去噪；峰值信噪比

数字图像在获取和传输过程中会受到不同程度的噪声干扰，这不仅直接影响图像的视觉效果，而且也给图像的后续处理带来一定的困难，如分割、识别、理解．因此图像去噪是数字图像处理的重要内容之一．传统的去噪方法在去除噪声的同时往往使图像变得模糊，丢失纹理的细节信息，给图像的后续处理带来较大影响，迫切需要有更好的算法来解决这个问题．

近几年来，分数阶微积分理论在图像处理方面得到了广泛关注及应用，在图像去噪方面也取得了一些进展．黄果等人[1-3]提出了基于Grmwald-Letnikov的分数阶积分图像去噪方法，更好地保留了图像的边缘和纹理细节信息．杨柱中等人[4]提出了利用分数阶微分梯度的图像去噪方法，有效地检测与去除了噪声，获得了更好的视觉效果．Zhang W等人[5]提出了非局部分数阶扩散波方程的图像去噪方法，有效地保留了图像边界区域．Zhang J等人[6]提出了基于分数阶微分的变分去噪模型，Chen等人[7]通过构造新的分数阶全变分模型，也均实现了图像去噪．He等人[8]在Grmwald-Letnikov分数阶微积分的基础上，构造相应的分数阶掩膜算子达到了去噪目的．上述文献说明基于分数阶微积分的图像去噪不仅可以实现较好的去噪效果，而且还可以保留图像平滑区域的纹理细节．本文提出的基于带权重的分数阶积分图像去噪算法，通过调节权重与阶次两个变量，使图像去噪效果达到最佳，并且实现了图像纹理细节的保留．

1　数字信号的分数阶表示

在欧氏测度下，由分数阶微积分Riemann-Liouville[9，10]的定义，v阶积分(v<0)的数字信号s(x)可表示为：

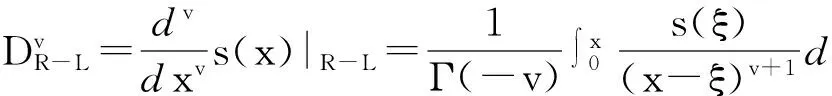
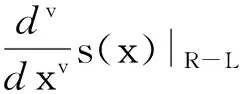
(2)

2　数字图像分数阶积分掩膜构建

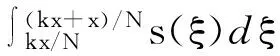
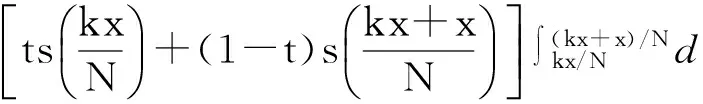
(3)

由(2),(3)式得：

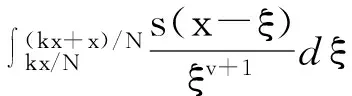
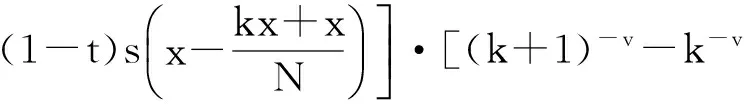
(4)

由(1),(4)式得：

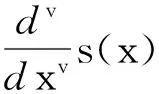
[(k+1)-v-k-v].

(5)

则由(5)式得到，二维图像信号s(x,y)在x轴与y轴方向的分数阶积分可以表示为：

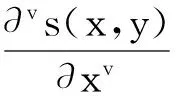
(6)

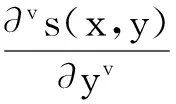
(7)

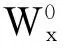
(8)

(9)

(10)

图1　8个方向的掩膜算子: 0°,45°,90°,135°,180°,225°,270°，315°Fig.1　Masks on eight directions: 0°,45°,90°,135°,180°,225°,270°，315°

3　数值实验及理论分析

为了客观评价图像的去噪效果，同时更好地与经典滤波方法(如均值滤波、高斯滤波、维纳滤波)作比较，本文采用峰值信噪比(PSNR[14])与信息熵(IE[8])作为去噪效果客观评价指标. 当PSNR值越大，说明算法的去噪效果越好；相反，PSNR值越小，说明算法的去噪效果不明显，其中PSNR表示为：

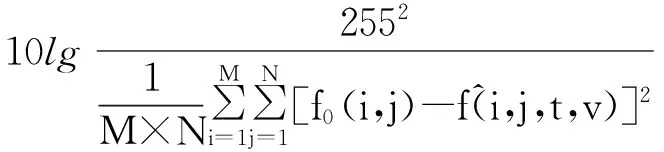
(11)

式中f0表示原始图像.当IE越靠近原始图像的IE，说明保留的图像纹理信息越多[15]，其中IE表示为：

(12)

式中p(i)，i=0,1,…，255表示图像各灰度级的概率，f表示图像.

实验采用大小为512×512的3种不同类型的灰度图像Lena、Peppers、Baboon，并在64位Window7 Matlab R2012b环境下进行．为了比较一般噪声图像的去噪效果，本文人为地对图像添加噪声，并分别取高斯噪声图像、椒盐噪声图像、泊松噪声图像进行实验，其中高斯噪声图像取均值为0，标准差σ分别为10,20,30的3组图像，椒盐噪声图像取噪声密度为0.05，所有掩膜算子大小均为3×3．图2为实验所采用的原始图像及相应的标准差为30的高斯噪声图像.

图2　实验图像Fig.2　Experimental images

根据(11)式知，标准差为30的Lena噪声图像去噪过程中所对应的权重t、分数阶v与PSNR可构成空间曲面，如图3所示，不同的t和v对应着不同的PSNR．通过调节t和v使PSNR达到最大值，其中t、v均取0.1的步长．

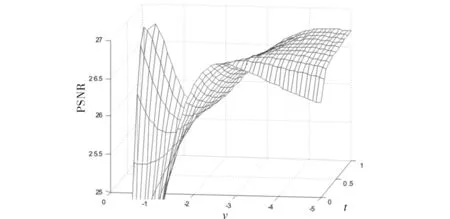
图3　t、v与PSNR构成的曲面Fig.3　The surface organized by t, v and PSNR

在进行去噪效果比较过程中，本文仅显示图像Lena、Peppers、Baboon在[150,300]×[150,300]区域上的去噪效果图，并均采用标准差为30的高斯噪声图像进行去噪处理．如图4～6所示，为图像的去噪效果比较，其每幅图像分别对应的是原始图像、噪声图像、均值滤波、高斯滤波、维纳滤波 、AFD滤波[13]、AFI滤波[13]和本文提出的方法．与均值滤波、高斯滤波、维纳滤波3种经典滤波作比较发现，本文提出的方法视觉效果最好，不仅噪声大幅度减少，而且图像纹理细节区域的信息得到了保留，没有产生模糊效果．高斯滤波处理效果不理想，明显地存在更多噪声．与文献[13]中提到的AFD滤波和AFI 滤波相比较，其视觉效果相当，且均滤除了大部分的噪声.

图4　不同滤波的图像去噪效果(图像Lena) Fig.4　Image denoising effect by different filters(Image Lena)

对不同类型噪声图像去噪后的实验数据进行整理，并与传统去噪算法作比较，记录PSNR达到最大值时所对应的t和v值．

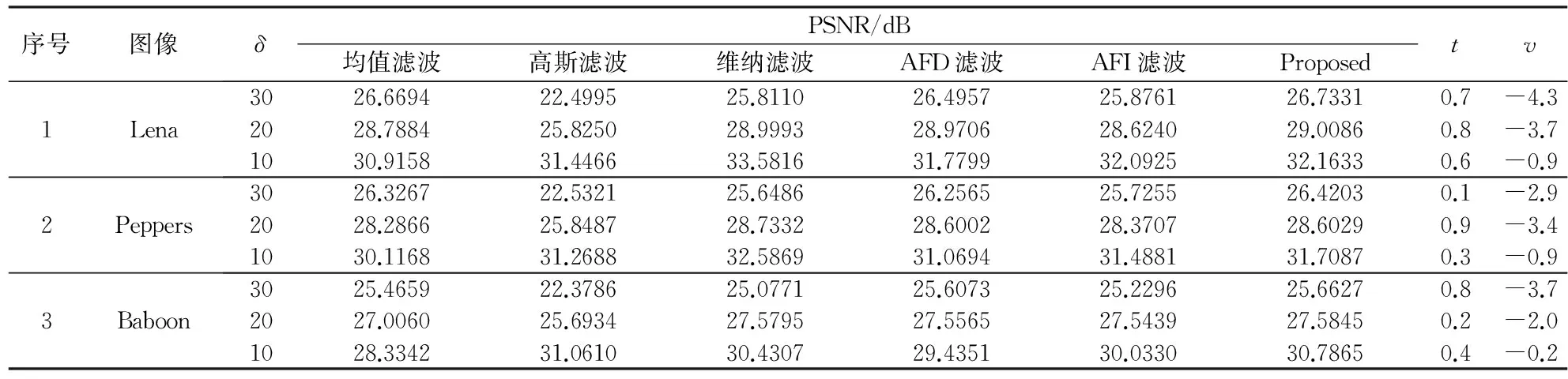
表1为不同类型滤波对不同标准差的高斯噪声图像去噪效果比较，以及当PSNR达到最大值时，本文算法所对应的t和v值. 从表1中可以看出，当高斯噪声的标准差比较大时，本文算法的PSNR值更大，说明当高斯噪声较多时，其去噪效果更加好．与高斯滤波作比较时发现，对于标准差较大的噪声图像，两者的差异更明显，本文算法的PSNR值均远远高于高斯滤波．

表2、表3分别对应不同类型滤波对椒盐噪声图像、泊松噪声图像去噪效果的比较，以及当PSNR达到最大值时，本文算法所对应的t和v值．从表2中可以看出，本文算法的PSNR值均大于传统的去噪滤波，略高于AFD滤波和AFI滤波，但却远远高出高斯滤波和维纳滤波．从表3可以看出，本文算法比均值滤波、高斯滤波去噪效果更好，同样也稍好于AFD滤波和AFI滤波.

表4为不同类型滤波IE值的比较，其中Δ表示各滤波处理图像与原始图像的IE差值的绝对值. 从表4可以看出，本文算法与高斯滤波、维纳滤波、AFD滤波、AFI滤波相比Δ更小，说明其IE值更接近原始图像的IE值，同时反映了本文算法保留了更多的图像纹理细节信息.

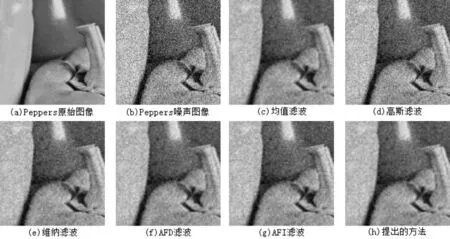
图5　不同滤波的图像去噪效果(图像Peppers)Fig.5　Image denoising effect by different filters(Image Peppers)

图6　不同滤波的图像去噪效果(图像Baboon)Fig.6　Image denoising effect by different filters(Image Baboon)

序号图像δPSNR/dB均值滤波高斯滤波维纳滤波AFD滤波AFI滤波Proposedtv1Lena3026.669422.499525.811026.495725.876126.73310.7-4.32028.788425.825028.999328.970628.624029.00860.8-3.71030.915831.446633.581631.779932.092532.16330.6-0.92Peppers3026.326722.532125.648626.256525.725526.42030.1-2.92028.286625.848728.733228.600228.370728.60290.9-3.41030.116831.268832.586931.069431.488131.70870.3-0.93Baboon3025.465922.378625.077125.607325.229625.66270.8-3.72027.006025.693427.579527.556527.543927.58450.2-2.01028.334231.061030.430729.435130.033030.78650.4-0.2

表2　不同类型滤波对椒盐噪声去噪效果比较

表3　不同类型滤波对泊松噪声去噪效果比较

表4　不同类型滤波信息熵比较

4　结束语

随着分数阶微积分理论在图像去噪方面的不断尝试，较好的去噪算法也会不断被提出．本文提出的基于带权重的分数阶积分去噪算法，通过调节两个参数，即权重t和积分阶次v，实现了较好的图像去噪效果．从实验结果可以看出，算法在实现图像去噪的同时，没有导致图像的纹理细节大幅衰减，同时保留了相应的信息内容．但本文算法存在一些不足，在今后的研究中需要重点解决的问题是：对于多节点信号如何有效设置权重来构造近似函数，如何与其他经典去噪算法相结合得到更好的去噪效果，如何根据图像的局部信息设定权重实现自适应图像去噪.

[1]Huang G, Xu L, Chen Q L, et al. Image denoising using fractional integral[J]. IEEE International Conference on Computer Science & Automation Engineering,2012,2:107-112.

[2]黄果，蒲亦非，陈庆利，等. 基于分数阶积分的图像去噪[J].系统工程与电子技术,2011,33(4):925-932.

[3]黄果，许黎，蒲亦非.分数阶微积分在图像处理中的研究综述[J].计算机应用研究,2012,29(2):414-420.

[4]杨柱中，周激流，郎方年. 基于分数阶微积分的噪声检测和图像去噪[J].中国图象图形学报,2014,19(10):1418-1429.

[5]Zhang W, Li J J, Yang Y P. A fractional diffusion-wave equation with non-local regularization for image denoising[J].Signal Processing, 2014,103(10):6-15.

[6]Zhang J, Wei Z. Fractional variational model and algorithm for image denoising[J]. International Conference on Natural Computation,2008,5:524-528.

[7]Chen D L, Sun S S, Zhang C R, et al. Fractional-order TV-L2 model for image denoising[J]. Central European Journal of Physics, 2013,11(10):1414-1422.

[8]He N, Wang J B, Zhang L L, et al. An improved fractional-order differentiation model for image denoising[J]. Signal Processing,2015,112:180-188.

[9]Oldham K B, Spanier J. The fractional calculus[M]. New York: Academic Press, 1974.

[10]McBride A C. Fractional calculus[M]. New York: Halsted Press, 1986.

[11]刘彦，蒲亦非，周激流. 一种基于分数阶积分的数字图像去噪算法[J]. 四川大学学报(工程科学版), 2011,43(3):90-95.

[12]Pu Y F, Zhou J L, Xiao Y. Fractional differential mask: a fractional differential-based approach for multiscale texture enhancement[J]. IEEE Trans Image Process, 2010, 19(2):491-511.

[13]Jalab H A, Ibrahim R W. Fractional Alexander polynomials for image denoising[J]. Signal Processing, 2015,107(C):340-354.

[14]Bovik A. Handbook of image and video processing[M]. New York: Academic Press, 2000:325-327.

[15]李博，谢巍. 基于自适应分数阶微积分的图像去噪与增强算法[J]. 系统工程与电子技术，2016,38(1):185-192.

Image Denoising Method for Weighted Fractional Integral

LouLiantang,FangZicheng,WeiXiyu,WuGaolin

(College of Mathematics and Statistics,South-Central University for Nationalities,Wuhan 430074,China)

In order to preserve more details of the image while image denoiseing, based on the fractional-order integral definition of Riemann-Liouville, this paper introduced weight parameters for the approximation process of digital signal, and proposed a method of the masks on eight directions by adjusting the value of weight and integral order. The experimental results show that compared with the traditional denoising methods, the proposed method not only can improve the peak signal-to-noise ratio of the image, but also can retain the image detailed texture better.

weight; fractional integral; image denoising; peak signal-to-noise ratio

2016-05-17 *通讯作者方自成，研究方向：数学应用方法与图像处理，E-mail：fzc0816@163.com

娄联堂(1966-)，男，教授，博士，研究方向：数学应用方法与图像处理，E-mail：louliantang@163.com

国家自然科学基金资助项目(60975011)；中南民族大学中央高校基本科研业务费专项资金资助项目(CZW15051；YZZ13003)

TP751.1

A

1672-4321(2016)03-0146-05