薄板总体隔声量与尺度关系研究
2016-10-31张振洲
张振洲
(1.兰州交通大学,甘肃 兰州 730070;2.中国科学院声学研究所南海研究站,海南海口570105)
薄板总体隔声量与尺度关系研究
张振洲1,2
(1.兰州交通大学,甘肃兰州730070;2.中国科学院声学研究所南海研究站,海南海口570105)
为了得到板材测试件尺度对隔声量的影响规律,本文主要通过薄板弯曲振动模型,讨论了安装边界的约束影响,从理论上研究了单层均匀薄板总体隔声量与板尺度,特别是面幅尺度的关系,找出了板材测试件尺度对总体隔声量的影响范围和程度,对不同尺度板材隔声量测量及修正具有一定指导意义。最后将理论结果与相关实验数据进行对比,分析了一致性和存在问题,对进一步完善和扩展该理论有重要作用。
声学;隔声量;矩形薄板;尺度;弯曲振动
板材自身的隔声性能需要通过实验室测量来决定[1]。实验室测量环境对板材测试件的尺寸有明确要求[2,3]。然而很多情况下,测试件很难满足实验室的尺寸要求,而只能以非“标准尺寸”进行测量[4],那么这种尺寸的测量值与实验室要求情形下的测量值往往有较大偏差,从而不能真实反映板材的隔声性能。目前直接对板尺度影响隔声量的理论研究还较少[5],本文就此通过对薄板弯曲振动及其边界约束的分析,给出单层薄板总体隔声量与板尺寸的关系,从而解决非“标准尺寸”板材进行测试的可行性问题。
1 单层均匀薄板的总体隔声
单层均匀薄板在声场中的受激振动,常被看作是整体振动和弯曲振动的结合[6],并以此来求得板的整体隔声量。实际测量板构件隔声性能时,一般要将板按照测试洞口的尺寸安装在框架上,框架以边界的形式对板的整体振动造成阻性和抗性影响。因此,边界对板整体振动的约束影响可通过引入弹性系数和阻尼系数来描述[7]。板的整体运动方程可表示为:

依据对无限大均匀薄板整体振动的分析,有限大小均匀薄板整体振动的声阻抗率可表示为:
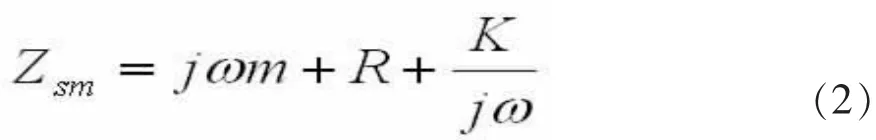
再考虑弯曲振动的声阻抗率,可得有限大小单层均匀薄板总阻抗率为:
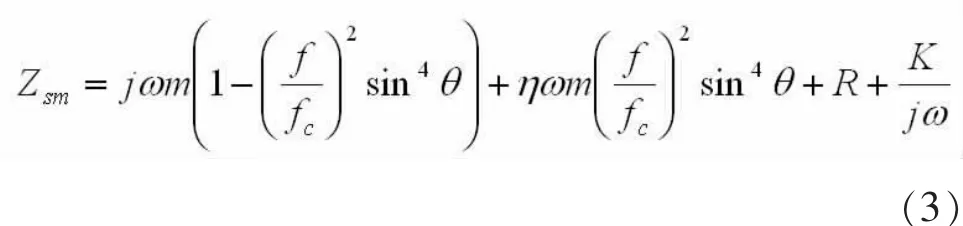
式中:fc——吻合频率;
η——损耗因子。
其隔声量可以依照定义得到:
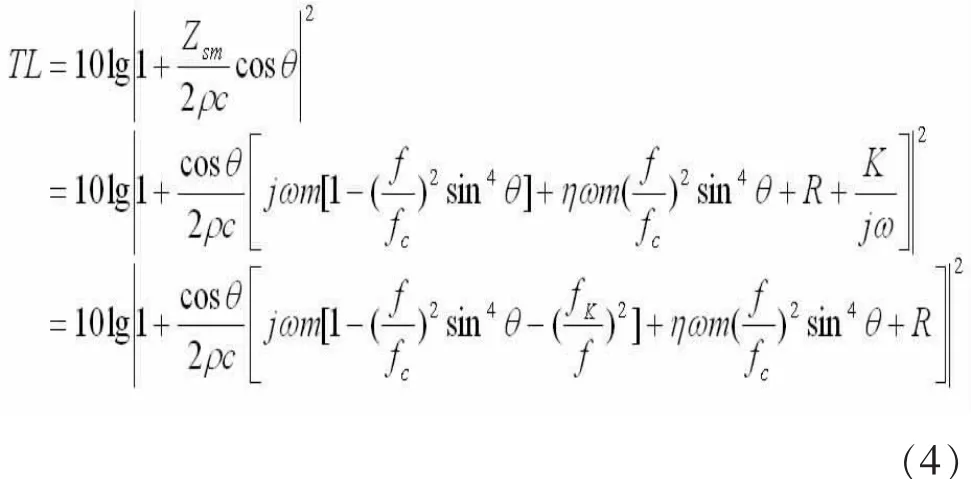
由(4)式可以看出,由于边界安装的影响,引入了板自身整体共振频率。在低频段,即f<
2 边界条件的讨论
安装边界对板振动的影响主要体现在弹性和阻性作用上,而这种作用主要存在于板的边缘上,因此,边界的影响是与板的尺度有关的。为了说明这种关系,分别考虑板边缘受到的弹性和阻尼约束的分布情况,如图1所示。可以将板边缘等效成弹簧阻尼分布系统,弹簧或阻尼都是以并联形式分布于边界上,设弹性系数和阻尼系数沿边界C的分布函数为κi和yi,则板整体振动总的弹性系数和阻尼系数可表示为:
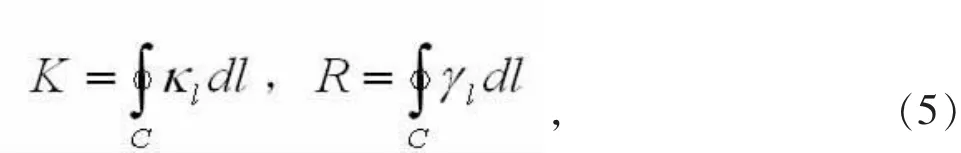
最常见的边框安装形式是四周安装方式一致的矩形情况。此时板边界弹性和阻尼分布均匀,而与边缘位置无关,总体弹性系数和阻尼系数为
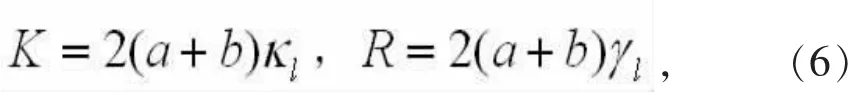
当然,如果边界安装方式不完全一致,可以分段计算弹性系数和阻尼系数。
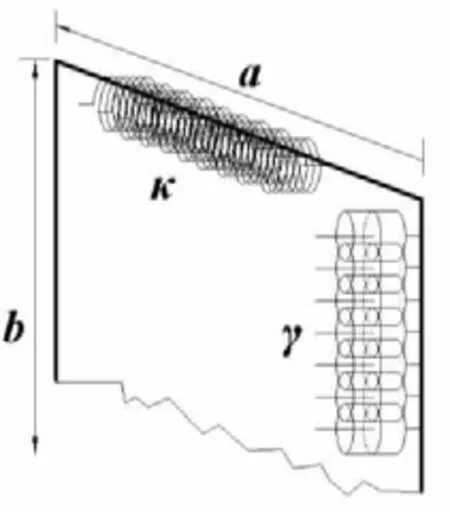
图1 板安装边界是弹性阻尼分布
3 总体隔声与尺度关系
3.1尺度对隔声量影响分析
将(2)式代入(4)式可得到四周安装方式相同的矩形均匀薄板总体隔声量为
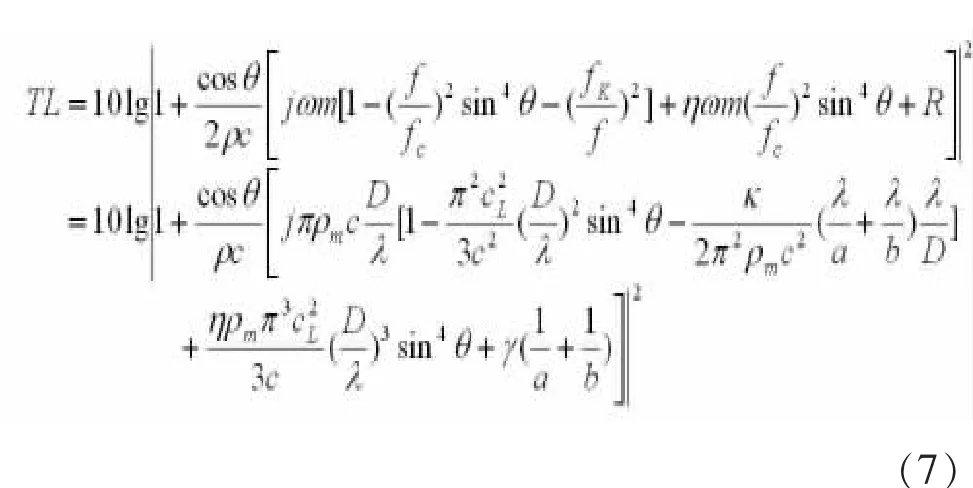
可以看出,总体隔声量与板的尺度因素有关,特别是面幅尺度的影响。如果其他因素相对确定,则对厚度与波长的讨论如下:
1)当板D<<λ厚度时,隔声量受板自身弯曲振动影响较小,受边界弹性和阻尼的共同影响较大,此时即对应薄板或低频时的情形,因为厚度相对越小,即波长相对越大,对应频率相对越低。如果板的相对面幅尺度满足:
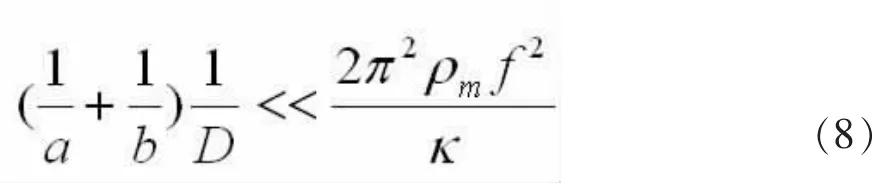
则隔声量可近似为:
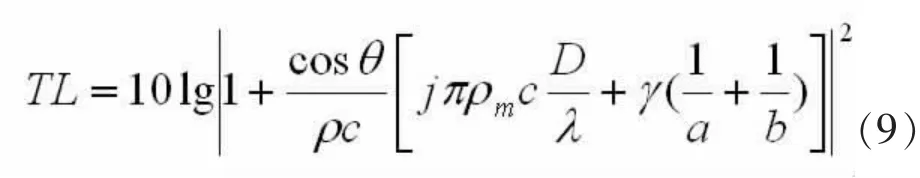
隔声量此时由边界阻尼影响较大,阻尼系数越大,隔声量越大;边界面幅尺寸越大隔声量越小。当面幅尺寸足够大时,阻尼影响逐渐消失,从而隔声量变成无穷大板整体振动的情形,即此时板的隔声量与面幅尺度无关,各尺度板均可按无穷大板来处理。如果板的相对面幅尺度满足:
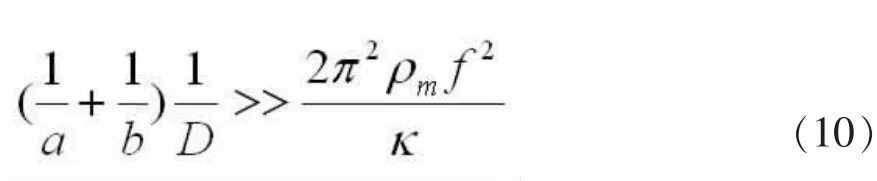
则隔声量可近似为:
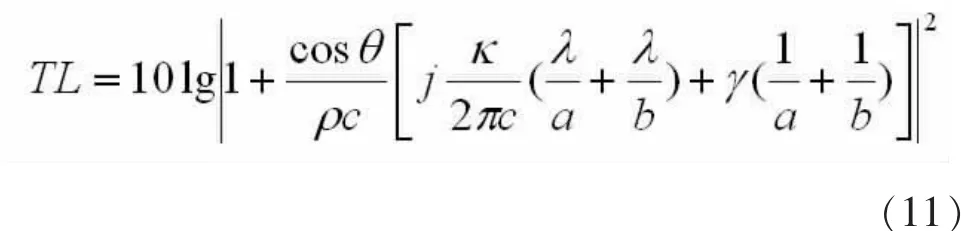
隔声量此时由边界弹性和阻尼共同影响,弹性或阻尼系数越大,隔声量越大;由于面幅尺度此时不能太大,因此,板的面幅尺度与波长相比越小,弹性贡献越大。
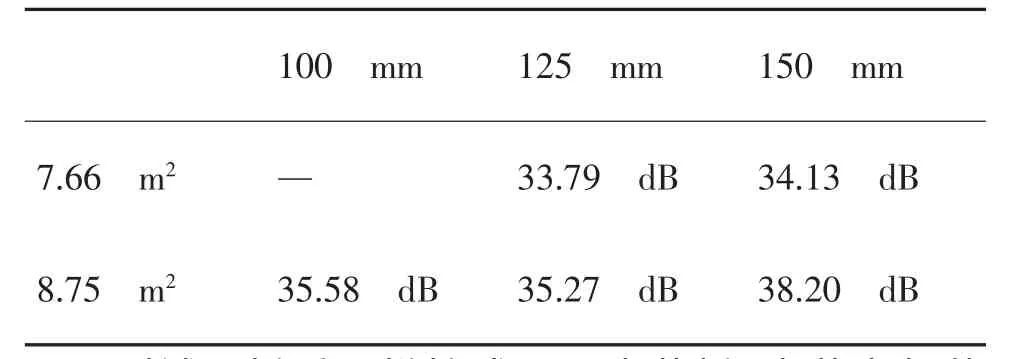
2)当板厚度D< 3.2计算与实验对比 为了突出隔声量与尺度的关系,将透射系数tI= 10-TL/10分别按入射角θ和频率f积分 则对于一定厚度的薄板,其对频段[f1,f2]无规入射声波的总体隔声量可表示为: 例如,对于扩散场中100Hz~3.15kHz均匀分布频段,不同面幅尺度和厚度的铁隔板的总体隔声量计算值和混响室测量值如图2所示, 其中,混响室测试板材尺度规格及相应的总体 图2 不同尺度的均匀铁板隔声量比较 隔声量见表1。 表1 各尺度规格铁板总体隔声量平均测量值 测试隔板采用拼接式双层夹芯板,夹芯为絮状吸声材料;安装边框采用水泥砌筑。 4.1总体隔声量与尺度关系 图2不仅反映了隔板厚度与总体隔声量的正相关性,而且反映了面幅尺度增大导致隔声量下降的规律,只有面幅尺度增大到一定程度后,隔声量才变化很小,此时不同尺度的板隔声量近似相等。 同时,相同面积但不同形状的板的总体隔声量略有不同,这与形状差异程度有关,形状差异越大,隔声量的差异也越大。 4.2遗留问题 1)理论曲线与测量值尚存偏差的可能原因有很多,如测试用板是双层夹芯板[8]而非单层板,安装边框的等效弹性分布和阻尼分布取值不精确,混响室精度限制等。 2)本文仅从弯曲振动模型入手研究整体隔声量与尺度的关系,并未涉及振动本身的模态分析[9]。 3)对边框安装的连接方式未作讨论,目前更适用于简支安装情况。 [1]钱中昌,寇毅伟,刘碧龙,等.同一实验室条件下不同隔声测量方法的探讨[J].声学技术.2013,32(6):495-499. [2]GBT19889.3-2005,声学建筑和建筑构件隔声测量第3部分:建筑构件空气声隔声的实验室测量[S]. [3]ISO 140-3-1995,Acoustics-Measurement of sound insula tioninbuildingsandofbuildingelements-Part3:Laboratory measurements of airborne sound insulation of building ele ments[S]. [4]宋拥民,盛胜我.小尺寸构件隔声测量方法的研究[J].噪声与振动控制.2002(5):34-36. [5]NataliyaS,VitaliyD.TheEvaluationoftheSoundInsulationof Partition in Expanded Frequency Range[J].Journal of Physi calScienceandApplication.2013,3(4):249-255. [6]JamesF.Doyle.WavePropagationinStructures[M].NewYork:Springer-Verlag,1997. [7]何琳,朱海潮,邱晓军,等.声学理论与工程应用[M].北京:科学出版社,2006. [8]卢天健,辛锋先.轻质板壳结构设计的振动和声学基础[M].北京:科学出版社,2012. [9]任惠娟,盛美萍.矩形薄板的模态声辐射效率[J].机械科学与技术.2010,29(10):1397-1400. O422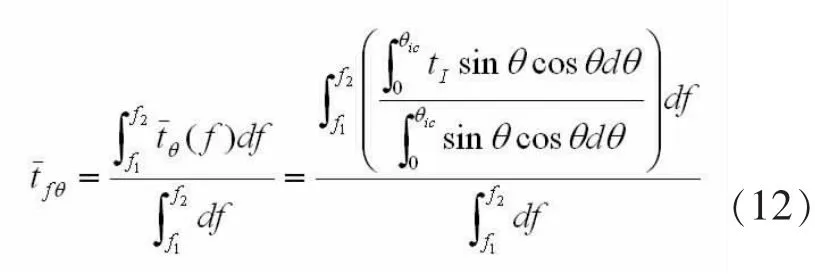


4 结论
