Harmonic Oscillator and Supersymmetric Harmonic Oscillator on Coordinate Dependent Noncommutative Space∗

Qurban Qeyum,Sayipjamal Dulat†,Mamatabdulla Hekim

(1.College of Physics Science and Technology,Xinjiang University,Urumqi Xinjiang 830046,China;2.Department of Physics,Hotan Teachers College,Hotan Xinjiang 848000,China)

Abstract: A three dimensional harmonic oscillator and it’s supersymmetric analogue on coordinate dependent noncommutative space de fined by a su(2)type noncommutative algebrawere discussed.At first,the energy corrections of harmonic oscillator due to noncommutativity were calculated,the result shows that harmonic oscillator obtains angular momentum related extra energy spectrum.Then,the hamiltonian of supersymmetric analogue of oscillator system on noncommutative space were obtained.Analyzing the supersymmetric hamiltonian,it shows that the system generates magnetic dipole interaction automatically as a direct consequence of this su(2)type noncommutative algebra.

Key words:noncommutative space;harmonic oscillator;supersymmetric

0 Introduction

In the past few years,noncommutative quantum mechanics has been studied comprehensively by a lot of researchers inspired by the development of String Theory[1]and considered as a theoretical tool that some ideas of Quantum Field Theory and String Theory can be realized with it.Much attention was focused on the canonical noncommutative space-time which realized by the coordinate operatorsi,i=1,...,N,and momenta operators,i=1,...,N,either satisfying the algebra

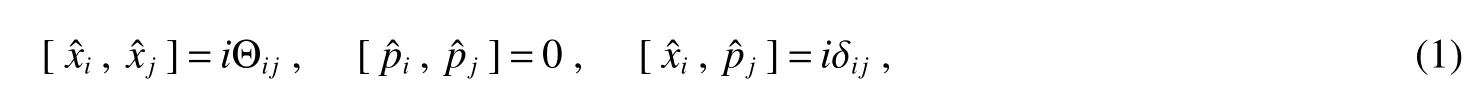
for noncommutative space,or satisfying the algebra

for both noncommutative space and noncommutative phase space.The constant parameters Θijandare totally antisymmetric matrices which represent the noncommutative property of the coordinate and momentum on noncommutative space and phase space respectively.

So far,there has been many works devoted to different aspects of physics in the frame of canonical noncommutative model featured with constant noncommutativity parameters ΘijandFor example,Aharonov-Casher effect[2],Aharonov Bohm effect[3,4],Landau problem[5],spin-hall effect[6]as well as other general phenomenological impacts of the noncommutativity has been extensively studied.

However,the canonical noncommutativity breaks the symmetry of the physical systems,like the rotational symmetry of the Coulomb problem[7,8],the Lorentz symmetry of field theoretical models[9].the symmetry violation is caused by the noncommutativity parameter Θijbeing a constant tensor,we can see that the commutation relationship[]in Eq.(1)should transform as a tensor under rotations,but constant Θijdoes not transform.Due to this problem,recently some researchers tried to formulate more generalized form of noncommutative quantum mechanics where the symmetry can be conserved,and proposed a new model which can be presented by commutation algebra[13]

with coordinate dependent operatorbeing the parameter of noncommutativity,and α being the formal deformation parameter.The star product which corresponding to the algebra(3)was formulated in Ref.[13]up to forth order of α,and the star product conform to second order α were given as

In this paper,we will apply su(2)type noncommutative algebra Eq.(5)on harmonic oscillator system as well as supersymmetric analogue of harmonic oscillator system[14,15]and discuss the effects that directly caused by the this type of noncommutativity.

1 Harmonic Oscillator on Coordinate Dependent Noncommutative Space

In noncommutative quantum mechanics,we just need to replace the usual product with the star product,then the Schrdinger equation will become the quantum mechanics equations in noncommutative quantum mechanics.LetH(x,p)be the hamiltonian in the usual quantum mechanics,the Schrdinger equation in noncommutative space

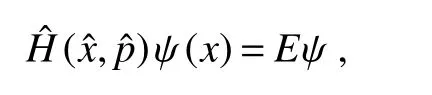
can equivalently be rewritten with star product in commutative space as

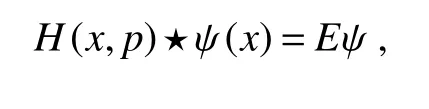
where parametersxandpare commutative quantum mechanics operators satisfying the Heisenberg algebra

For a physical problem in noncommutative quantum mechanics,If the relative star product were de fined,it could easily be transilated to usual quantum mechanics problem.Then we can discuss it in usual quantum mechanics frame.

Let us consider a three-dimensional noncommutative harmonic oscillator on noncommutative space de fined in Eq.(5)described by the Hamiltonian

As far as the algebra(5)is concerned,takingsubstituting them into Eq.(4)and after rearranging the index notations,we can reconstruct star product for algebra(5).The modi fied star product reads

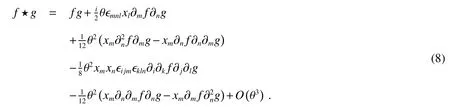
For the case of harmonic oscillator in noncommutative space,the Schdinger equation reads

by using Eq.(8),we can calculatex2?ψ(x),and it yields

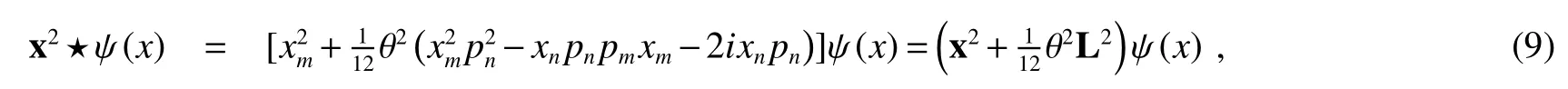
where L2==1,2,3 andLiis the usual angular momentum operator.We used formula

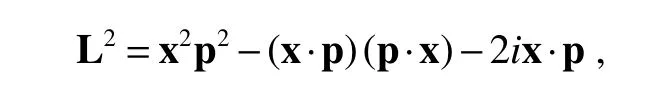
in last step of Eq.(9).

whereH0=can be concerned as perturbation term.Using perturbation formula

we can now calculate the first order energy correction

where|ψ0i is unperturbed wave function,andlis the orbital quantum number.

2 Supersymmetric Harmonic Oscillator on Coordinate Dependent Noncommutative Space

A supersymmetric non-relativistic noncommutative quantum mechanics model that dipole interactions can be automatically generated as a consequence of particular commutative realization of some algebra were proposed[14].In order to do so we will consider a system on coordinate dependent noncommutative space,and apply supersymmetric realization procedures described in Ref.[15,16]on the system,then analyze the impacts of noncommutativity.

We have calculated harmonic oscillator in previous section,in this section we will consider the supersymmetric version of that model.For a harmonic oscillator the hamiltonian also can be written as

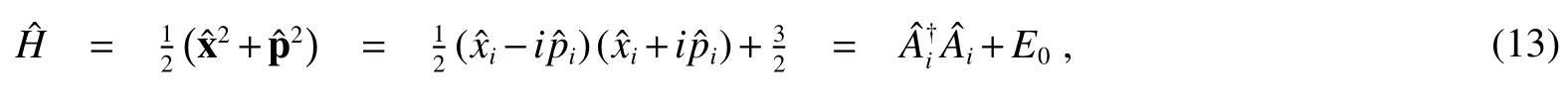
whereE0is the ground state energy,and

are respectively creation and annihilation operators in noncommutative space.

Using Eq.(6),restricting θ to the first order,we have the following set of representation

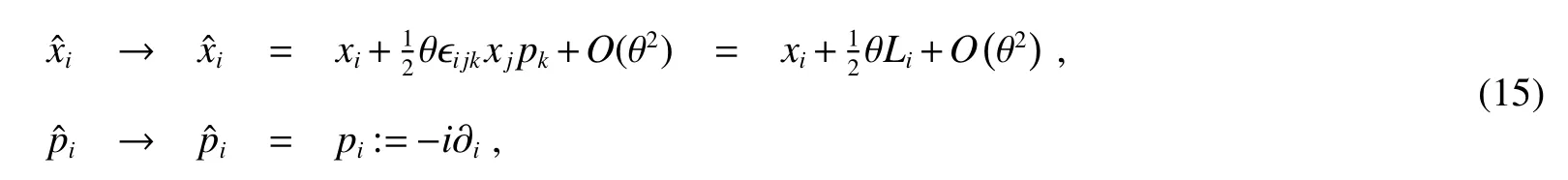
whereLiis the normal angular momentum operator in commutative space.

Referencing Eq.(5),replacing thewith respective representation showed in Eq.(15),the The following set of commutation relationships can be formulated

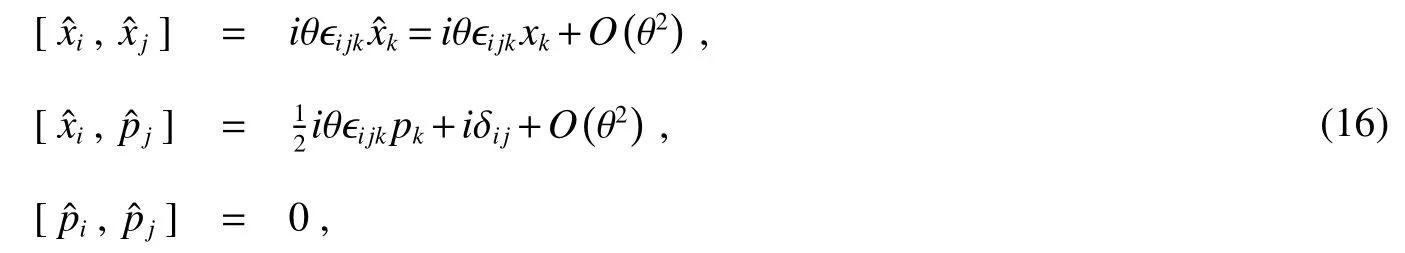
Notice that Eq.(16)is just the respective basic commutation relationships that related with first ordered θ,and it changes to standard Heisenberg algebra when θ=0.by using Eq.(15)and Eq.(16)The commutation relationships betweenandnow become

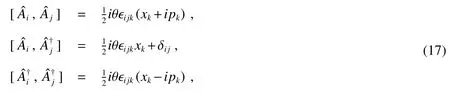
Note that the commutation relationships in Eq.(17)are same as those in the commutative case under the limit θ→ 0.

Following the supersymmetrization procedure proposed in[15,16],the supercharges are de fined as follows

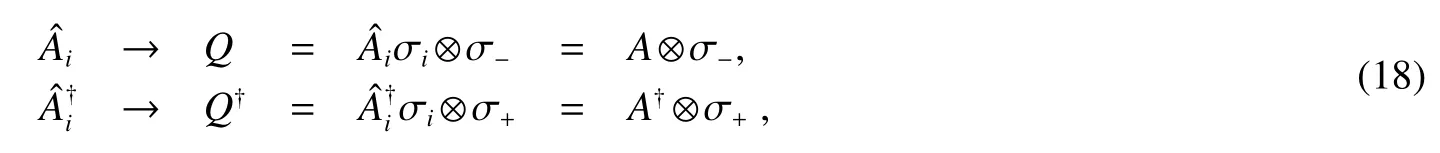
where σiis pauli matrices,

The supersymmetric Hamiltonian is de fined as the non-negative operator.

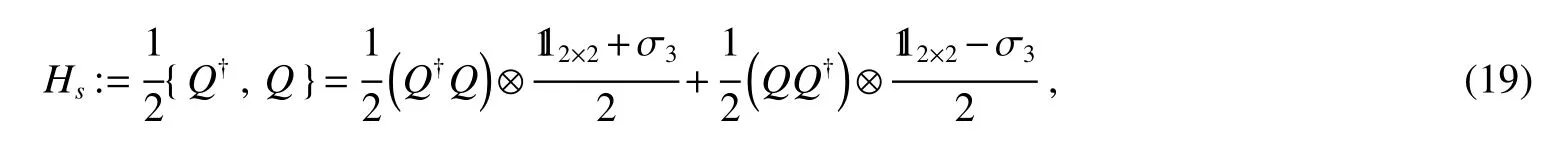
or we can equivalently write it as

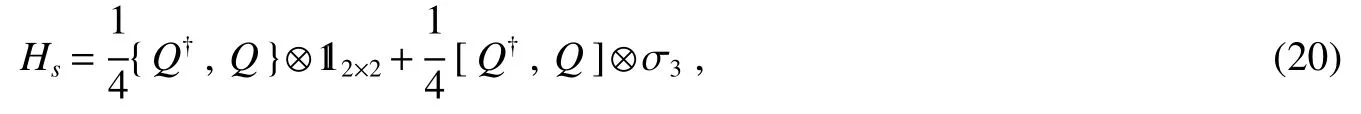
notice that this Hamiltonian is de fined on a space of four component functions(a pair of spinors),

And we get following commutation relationships with the supercharges

Substituting Eq.(18),Eq.(15)into Eq.(20),the supersymmetric hamiltonian reads

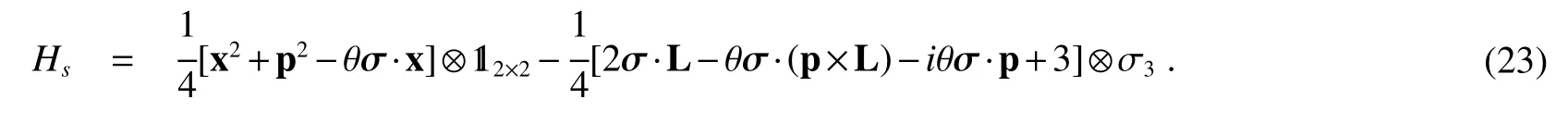
The hamiltonian obtained in Eq.(23)gives some intersting consequence of choosen su(2)type noncommutative algebra,such as the Magnatic-dipole interactions item σ ·x were generated as expected,besides that,the hamiltonian contains σ ·L and σ ·p items which are respectively refers spin-orbit coupling and Dresselhaus interactions.

3 Conclusion

In this paper firstly,we have calculated the harmonic oscillator system in noncommutative quantum mechanics which preservs the symmetry of the angular momentum.As a result harmonic oscillator obtained angular momentum related extra energy spectrum.The corresponding energy correction were explicitly calculated,Besides,we have tried to demonstrate that this algebra generates magnatic-dipole interactions in a supersymmetric system on noncommutative space.Indeed,the supersymmetric hamiltonian implies that the system obtains magnatic-dipole effect as well as spinorbit coupling and Dresselhaus interactions.