分层认知无线电网络中基于稳定匹配的资源分配算法

曹 龙 赵杭生 鲍丽娜 张建照



分层认知无线电网络中基于稳定匹配的资源分配算法

曹 龙*①②赵杭生②鲍丽娜③张建照②

①(解放军理工大学通信工程学院 南京 210007)②(南京电讯技术研究所 南京 210007)③(中国联通江苏分公司 南京 210019)

频谱资源的合理分配是认知无线电技术追求的目标之一，随着认知无线电网络中的次用户(SUs)数量不断增加，频谱资源的精确、实时分配与管控越来越难以实现。针对此问题，该文提出一种分层的认知无线电网络(CRN)架构，多个管理实体专注于为各层用户提供频谱服务；并在该架构下，提出一种基于稳定匹配的资源分配算法，用户通过自主协商形成分配结果，不仅保证了主用户(PUs)对次用户的功率限制，还充分考虑了各自的效用。仿真结果表明，所提算法的性能接近于最优方案，并降低了计算复杂度和系统时延。

认知无线电；资源分配；匹配理论；稳定匹配；最优化

1 引言

移动互联网、物联网以及智能终端的出现带来了便捷的生活方式和良好的用户体验(Quality of Experience, QoE)，不断增长的多媒体业务对带宽和数据速率的要求越来越高，相关机构预测到2020年无线网络流量将是2010年的1000倍[1]，如何高效地利用有限的频谱资源成为工业和学术界关注的重点[2,3]。

认知无线电(Cognitive Radio, CR)[4]技术的出现提高了频谱利用率，在不影响主用户(Primary Users, PUs)通信的前提下，次用户(Secondary Users, SUs)能够接入空闲的PUs频段。CR网络(CR Networks, CRNs)内PUs和SUs共存，资源分配技术能够合理地将空闲频段分配给SUs，提高了频谱利用率，减小了SUs间、SUs与PUs间的干扰。

目前的资源分配方法大多都只考虑SUs的效用函数，例如吞吐量、能量有效性和对PUs的干扰限制等，博弈论利用SUs间的竞争关系进行建模，求解问题的均衡解[9]，然而联合考虑PUs和SUs性能的研究尚不多。

本文首先提出了一种分层的CRNs架构，支持异构认知无线网络，利用多个管理实体为用户提供频谱服务。在此基础上，提出了一种新的资源分配算法用于SUs接入授权信道过程。利用经济学中的双边匹配理论，将该过程建模为一对一匹配问题，SUs和PUs根据设计的效用函数生成偏好信息，通过自主协商形成最终“稳定”的资源分配方案，降低了计算复杂度和系统时延，提高了频谱资源利用率。

2 分层认知无线电网络

如图1所示，分层的CRNs包括3层：管理层、网络层和用户层。管理层由频谱服务中心(Spectrum Service Center, SSC)、频谱管理人员和数据中心组成，SSC通过解析国际、国内、地区、地域等不同范围的频谱使用管理规则、规定、政策，监测频谱使用情况，收集、梳理、分析频谱使用信息，分析和预测频谱使用形势和变化趋势，对频谱服务提供商(Spectrum Service Providers, SSPs)的频谱服务请求做出响应，分配可用的授权频谱；数据中心主要存储数字化的频谱政策[10]、用频案例和频谱监测数据等。网络层由频谱服务提供商和基础网络组成，SSPs主要向网络内的用户提供用频服务，综合全网的用频需求、用户体验(Quality of Experience, QoE)和经费预算等向SSC租借频谱，在指定的时间和区域享有部分授权频谱的独占式使用权。SSC与SSPs可以是无线或有线连接，按照规定的格式(例如频谱消费模型[10])进行数据交互，相互之间是松耦合的关系。用户层内的用户终端(User Equipments, UEs)主要包含PUs和SUs, PUs同样会根据自身的用频需求、QoE和预算等向SSPs租借频谱，而SUs可以采用频谱感知、频谱数据库访问[11,12]等方法进行机会式频谱接入(Opportunistic Spectrum Access, OSA)。

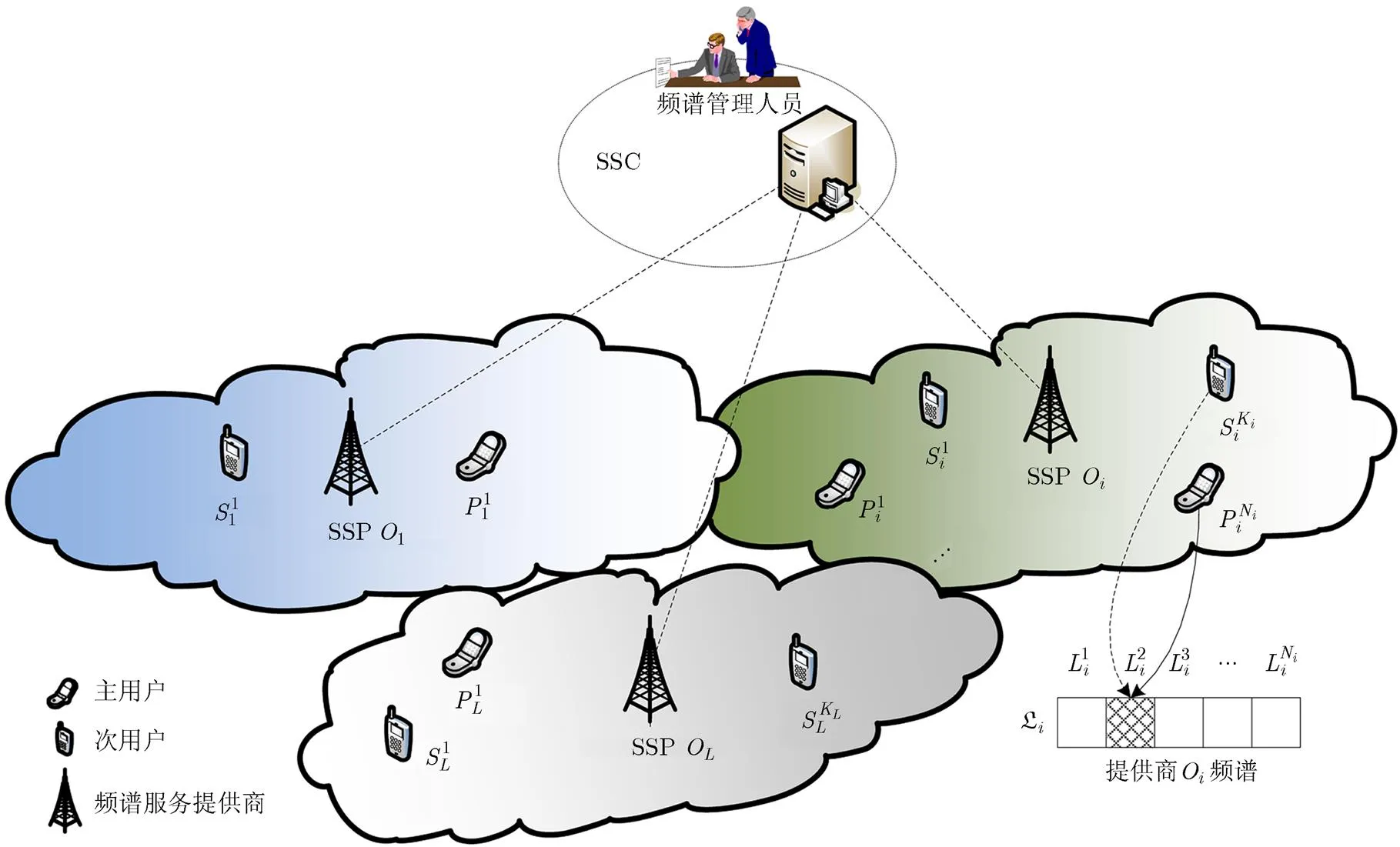
图1 分层认知无线电网络

分层的CRNs是一个异构无线网络，同一SSP内可以采用不同的接入方式，例如PUs采用蜂窝移动方式，而SUs采用WiFi或D2D(Device-to-Device)方式；不同SSPs也同样可以采用不同的接入方式。

图1所示的网络内包含多个频谱分配(指配)过程：(1)SSC将一段时间、特定区域内可用频谱分配给SSPs; (2)SSPs将拥有的授权频谱分配给本网PUs; (3)SUs根据用频需求选择接入PUs拥有的频段。本文重点研究SSP网络内SUs接入PUs拥有的授权频段(即第3个过程)，提出的基于稳定匹配的资源分配算法也可以推广到其它分配过程。

3 系统模型

考虑授权频段被均匀地划分为多个带宽相等、相互正交的子信道，每个SSP拥有一定数量的子信道，SSC分配给SSP的信道集合，并且、每个子信道带宽为；设SSP为个SUs集合提供频谱服务。每个授权子信道都分配给一个PU，假设占用子信道的PU为，因此主用户集合；如果该子信道空闲则有,SSP内活动的PUs集合。PUs是授权频谱的租赁者，在不影响自身通信质量的前提下，PUs允许SUs机会式频谱接入，并且可以选择Overlay和Underlay两种接入方式。假设SU最多只能选择一个授权信道，而每个子信道最多也只能被一个SU占用，这样SSP就能够很容易地计算和排除PUs受到的干扰。系统模型如图2所示。

图2 系统模型

SUs可以采用Overlay和Underlay两种接入方式利用授权频段[13]：当PUs空闲，SUs采用Overlay接入方式，SUs发射机可以根据自己的需求采用合适的发射功率；当PUs工作，SUs采用Underlay接入方式，SUs发射机的发射功率必须满足PUs或是SSP的限制要求。

同理由于每个SU也只能接入单个授权信道，可以得到约束条件：

3.1 次用户的效用函数

假设SU采用Overlay接入方式时，SU发射机以最大发射功率进行通信，则SU在授权信道上可获得的平均可达速率(机会速率)可以表示为

假设SU采用Underlay接入方式时，SU发射机以不大于信道规定的最大发射功率进行通信，同理，此时的平均可达速率可以表示为

3.2 主用户的效用函数

PUs作为授权信道的拥有者，资源分配时应考虑其由于频谱共享而受到的影响。当SU采用Underlay方式接入时，授权信道上PU的可达速率会受到干扰功率的影响；SSP将根据SU可获得的速率、QoE等制定差异化的付费规则，并且PU愿意将授权信道租借给付费高的SU，因此将PU的效用函数设计为可达速率与收入的乘积。

4 基于稳定匹配的资源分配算法

在传统的集中式方法中，管理实体通常会选取一个全局效用作为求解的目标函数，这里选择PUs和SUs效用函数的加权和。

式(8)是0-1整数规划问题，其复杂度为指数幂，并且随着网络规模的增大而急剧变大。传统的匈牙利算法通过集中式方案进行求解[14]，然而在实际执行中通常需要设立协调中心专门负责计算和资源协调分配，此外IBM公司开发的CPLEX应用程序也可用于求解此类问题[15]。

SUs选择接入PUs占用的授权子信道可以看成双边匹配问题[16]，诺贝尔奖经济学奖获得者GALE和SHAPLEY[17]在1962年首先提出了典型匹配问题婚姻匹配，其性能与集中式方案相当但复杂度相当低[18]。实际上，匹配理论通常用于建模两个独立主体集合间的分配问题，一方主体(集合)内的个体对另一方主体(集合)内的个体存在偏好(preferences)关系，它反映该个体在选择对方主体(集合)中个体时的先后顺序。经济学中一般假设偏好是完全有序的、可传递的，在资源分配背景下该条件是完全满足的。通常以符号来表示个体的偏好，例如表示相比于个体，个体情愿选择。文献[19]给出了匹配理论中的部分定义，我们将其扩展到分层CRNs中的资源分配问题。

简而言之，相比于目前已经匹配的对象，两个个体都倾向于彼此称为阻塞对。

我们采用经济学中的G-S算法对资源分配问题进行求解，该算法通常用于求解一对一问题，扩展后可以求解多对一问题，广泛应用于美国住院医师匹配计划、大学生入学和肾脏移植等实际问题[21]。其算法计算复杂度低，并且性能与最优化算法相当。

表1算法主要步骤包含3个部分：初始化、SUs申请和信道(PUs)决策。算法具体实现步骤如表1所示，步骤1-步骤3进行算法的初始化，建立相应的矩阵和集合；步骤5, SUs根据偏好矩阵提出申请；步骤6，信道(PUs)对这些申请进行决策；重复上述步骤直到SUs的申请不被拒绝。当SSP网络的状态发生变化或下一个分配周期时，重复执行该算法。

表1 基于稳定匹配的资源分配算法实现步骤

定理1 表1算法的解是稳定的。

证明 算法步骤1根据式(5)和式(6)效用函数值的大小建立偏好矩阵，由于信道状态的随机性，,，同理,。因此匹配中不存在阻塞个体。,，满足，由算法步骤5可知：SU曾经向信道提出过申请；由可知：算法结束时，信道拒绝了SU的申请。根据算法步骤6可知，，满足。因此匹配中不存在阻塞对。综上，根据定义4可知，算法的解是稳定的。 证毕

定理2 表1算法的解对于SUs来说是弱帕累托最优的。

5 仿真结果与分析

仿真时考虑SSP网络部署在400 m×400 m的正方形区域内，子信道的数量分别取5和10, SUs的数量在动态变化。UEs的地理位置随机生成，图3给出了用户数最多时的用户分布示意图(PUs和SUs分别从序号最大的开始减少)。蓝色的代表PUs收发机，红色的代表SUs收发机，发射机为实心，而接收机为空心。PUs收发机之间的距离为120 m, SUs收发机之间的距离则为100 m。

图3 用户分布情况

为了说明算法性能，本文与式(8)的最优解和随机分配进行了对比，随机匹配的结果是106次仿真结果的平均值。

图4(a)，图5(a)给出了不同SUs数下效用值的比较，可以看出算法获得的全局效用值、SUs效用值与最优解非常接近，而PUs效用值略次于最优解，并且3种效用都远好于随机匹配，这是因为表1算法对于SUs来说是弱帕累托最优的。对比图4(a)和图5(a)，随着子信道数量的增多，SUs可用的频谱接入机会增加，SSP的全局效用、SUs效用和PUs效用都明显增大，也就是说向SSC申请到更多的授权信道对SSP内的SUs和PUs都有益。

图4 主用户数Ni=5的仿真结果

图5 主用户数Ni=10的仿真结果

图4(b)，图5(b)给出了不同SUs数下用户申请次数的比较，可以看出当用户数较少时()，用户申请次数小，这是因为此时接入授权信道的竞争小；随着用户数的增多，某些不受PUs偏爱的用户需要多次申请才能完成匹配。假设SU通过bit的数据向PU提出申请，该PU通过bit的数据反馈结果，根据图4(b)，图5(b)可以估算出基于稳定匹配的资源分配算法所带来的通信开销。

图4(c)，图5(c)给出了不同SUs数下算法的while循环次数比较，可以看出循环次数随着用户数的增多而增大。结合图4(b)和图4(c)，图5(b)和图5(c)可以看出，相同SUs数时算法的循环次数总是大于等于最大申请次数，这是因为在迭代过程中部分匹配对被新的申请所破坏。

6 结束语

本文提出了一种分层的认知无线电网络，多个管理实体为不同层的用户提供频谱服务。在此基础上，提出了适用于该分层架构的资源分配算法。利用经济学中的双边匹配理论，将该过程建模为一对一匹配问题，SUs和PUs根据设计的效用函数生成偏好信息，用户根据各自的偏好自主协商形成最终的资源分配方案。资源分配的目标不再是目标函数的最大化，而是获得系统稳定的弱帕累托解。仿真表明，该算法的性能接近于最优解，并且大大降低了计算复杂度和系统时延，所带来的通信开销也很小，有利于实际部署。

参考文献

[1] Osseiran A, Braun V, Hidekazu T,. The foundation of the mobile and wireless communications system for 2020 and beyond: challenges, enablers and technology solutions[C]. IEEE Vehicular Technology Conference, Dresden, 2013: 1-5. doi: 10.1109/VTCSpring.2013.6692781.

[2] Ahmad A, Ahmad S, Rehmani MH,. A survey on radio resource allocation in cognitive radio sensor networks[J].&, 2015, 17(2): 888-917. doi: 10.1109/COMST.2015.2401597.

[3] Vassaki S, Poulakis M I, and Panagopoulos AD. Spectrum leasing in cognitive radio networks: a matching theory approach[C]. IEEE Vehicular Technology Conference, Glasgow, 2015: 1-5. doi: 10.1109/VTCSpring.2015.7146101.

[4] Mitola J, Guerci J, Reed J,.Accelerating 5G QoE via public-private spectrum sharing[J]., 2014, 52(5): 77-85. doi: 10.1109/ MCOM.2014.6815896.

[5] Musavian LandAissa S. Capacity and power allocation for spectrumsharing communications in fading channels[J]., 2009, 8(1): 148-156. doi: 10.1109/TWC.2009.070265.

[6] Asghari V and Aissa S. Adaptive rate and power transmission in spectrum-sharing systems[J]., 2010, 9(10): 3272-3280. doi: 10119/TWC.2010.090210.100291.

[7] Zhou X, Li GY, LiD,. Probabilistic resource allocation for opportunistic spectrum access[J]., 2010, 9(9): 2870-2879. doi: 10119/ TWC.2010.070610.091511.

[8] 潘甦, 曹跑跑, 刘胜美. 一种多无线电系统中基于公平性和精细化带宽分配的资源分配算法[J]. 电子与信息学报, 2015, 37(2): 399-404. doi: 10.11999/ JEIT140339.

Pan S, Cao P, and Liu S. A resource allocation algorithm based on proportional fairness and refined bandwidth allocation for multi-radio systems[J].&, 2015, 37(2): 399-404. doi: 10.11999/ JEIT140339.

[9] Xu Y, Anpalagan A, Wu Q,. Decision-theoretic distributed channel selection for opportunistic spectrum access: strategies, challenges and solutions[J].&, 2013, 15(4): 1689-1713. doi: 10.1109/ SURV.2013.030713.00189.

[10] IEEE 1900.5-2011. Standard for policy language requirements and system architectures for dynamic spectrum access (DSA) systems [S]. 2011.

[11] Al-Ali AK, SUN Y, FELICE M D,. Accessing spectrum databases using interference alignment in vehicular cognitive radio networks[J]., 2015, 64(1): 263-272. doi: 10.1109/TVT.2014. 2318837.

[12] Chen X and Huang J. Database-assisted distributed spectrum sharing[J]., 2013, 31(11): 2349-2361. doi: 10.1109/ JSAC.2013.131110.

[13] Goldsmith A, Jafar SA, Maric I,. Breaking spectrum gridlock with cognitive radios: an information theoretic perspective[J]., 2009, 97(5): 894-914. doi: 10.1109/JPROC.2009.2015717.

[14] Papadimitriou C H and Steiglitz K. Combinatorial Optimization: Algorithms and Complexity[M]. New York,USA, Dover Press, 1998: 248-255.

[15] IBM. Cplex optimizer[OL].http://www-01.ibm.com/software/commerce/optimization/cplex-optimizer, 2016.

[16] Gusfield D and Irving RW. The Stable Marriage Problem: Structure and Algorithms[M]. Cambridge, MA, USA, MIT Press, 1989: 1-8.

[17] Gale D and Shapley LS. College admissions and the stability of marriage[J]., 1962, 69(1): 9-15. doi: 10.2307/2312726.

[18] Gu Y,Saad W, Bennis M,. Matching theoryfor future wireless networks: fundamentals and applications[J]., 2015, 53(5): 52-59. doi: 10.1109/ MCOM.2015.7105641.

[19] Jorswieck E. Stable matchings for resource allocation in wireless networks[C]. International Conference on Digital Signal Processing (DSP), Corfu, 2011: 1-8. doi:10.1109/ICDSP.2011.6004983.

[20] Naeem M, Anpalagan A, Jaseemuddin M,. Resource allocation techniques in cooperative cognitive radio networks[J].&, 2014, 16(2): 729-744. doi:10.1109/SURV.102313.00272.

[21] Manlove D F. Algorithmics of Matching Under Preferences[M]. Singapore, World Scientific Press, 2013: 1-47.

Resource Allocation Algorithm Based on Stable Matching in Hierarchical Cognitive Radio Networks

CAO Long①②ZHAO Hangsheng②BAO Lina③ZHANG Jianzhao②

①(,,210007,)②(,210007,)③(,,210019,)

The rational spectrum resource allocation is one of the goals of Cognitive Radio (CR) technology. With the rapid increase of Secondary Users (SUs) numbers, the precise and real-time management becomes more and more difficult to achieve.In order to solve this problem, a hierarchical Cognitive Radio Network (CRN) architecture that several administration entities focus on providing spectrum services for users of variety tiers is proposed. The corresponding resource allocation algorithm based on stable matching in this architecture is also given. This algorithm guarantees the restriction on SUs’ transmission power for Primary Users (PUs), and also considers both utility functions of users. Simulation results demonstrate that the proposed method can roughly achieve the same performance of optimal solution with lower computation complexity and system delay.

Cognitive Radio (CR); Resource allocation; Matching theory; Stable matching; Optimization

TN929.5

A

1009-5896(2016)10-2605-07

10.11999/JEIT151460

2015-12-24；改回日期：2016-05-26；网络出版：2016-07-14

曹龙 caolong460@sohu.com

国家自然科学基金(61471395, 61471392, 61301161)，江苏省自然科学基金(BK20141070)

The National Natural Science Foundation of China (61471395, 61471392, 61301161), The Natural Science Foundation of Jiangsu Province (BK20141070)

曹 龙： 男，1988 年生，博士生，研究方向为认知无线电、动态频谱管理.

赵杭生： 男，1962 年生，研究员，博士，研究方向为认知无线电、动态频谱管理.

鲍丽娜： 女，1987 年生，工程师，硕士，研究方向为网络资源管理、认知无线电.

张建照： 男，1985 年生，工程师，博士，研究方向为认知无线电、Ad Hoc网络、动态频谱管理.