基于功能原理和模糊控制的路面附着系数估计*

林柏忠　李振洋　何磊　宗长富

(吉林大学 汽车仿真与控制国家重点实验室， 吉林 长春 130022)



基于功能原理和模糊控制的路面附着系数估计*

林柏忠李振洋何磊†宗长富

(吉林大学 汽车仿真与控制国家重点实验室， 吉林 长春 130022)

为从根本上解决轮胎参数变化影响估计精度的问题，文中不引入轮胎模型，提出了一种基于功能原理和模糊控制的路面附着系数估计算法.首先利用功能原理推算当前车辆状态下的利用附着系数，再通过模糊推理的方法由当前状态下的利用附着系数和滑移率推算当前行驶路面的峰值附着系数，然后利用Matalb软件建立车辆的三自由度模型，对估计算法进行了仿真分析.结果表明，文中算法能有效地估计路面附着系数，具有良好的实时性和准确性.

功能原理；模糊逻辑；路面附着系数；估计算法

在车辆行驶过程中，除空气阻力外，绝大部分作用于车辆上的外力均来自于轮胎与地面间的接触力，因此轮胎与路面间的接触情况对车辆的安全性和动力性等性能起着决定性的作用.路面附着系数表征轮胎与路面间的接触情况，也限制了轮胎可获得的最大路面作用力，因此，路面附着系数是影响主动避撞等主动安全系统性能的关键参数.目前，识别路面附着系数的传感器无法适应汽车行驶过程中复杂的工况，有关其研究仍然处于试验阶段，尚未在实际车辆运行中使用[1]，因此需要对路面附着系数进行实时估计.

为了实现对路面附着系数的实时估计，进而改善车辆主动安全系统的性能，国内外学者在路面附着系数估计领域进行了大量的研究.文献[2-3]利用轮胎的切向振动来估计路面附着系数；文献[4]将最大路面附着系数看作路面附着系数、滑移(转)率、垂向载荷的函数，利用瞬时摩擦系数和瞬时滑移(转)率估算最大路面附着系数；文献[5]利用单轮模型和各向异性的刷子模型推导出轮胎纵向力与路面附着系数之间的关系，从而求出路面附着系数；文献[6]利用扩展双卡尔曼滤波器同时估计车辆的运行状态和路面附着系数，并互为修正；文献[7]利用能量守恒定律对路面附着系数进行实时估计.在上述算法中都引入了不同的轮胎模型，使得这些算法对轮胎参数的变化十分敏感，而车辆在实际行驶过程中，胎压、垂向载荷、路面情况的变化都将导致轮胎参数的变化，从而导致上述算法估计精度的下降.为解决上述问题，文献[8]引入修正算法对轮胎参数进行实时修正，但轮胎参数大多是非线性的，这导致了算法更为复杂，无法保证实时性.因此，利用已有算法很难兼顾算法的准确性和实时性.

为从根本上解决因轮胎参数变化而影响算法精度的问题，文中不引入轮胎模型，提出了一种基于功能原理和模糊控制的路面附着系数估计算法，即利用动能变化量等于系统受到的外力功和模糊控制器进行路面附着系数的估计.

1　车辆模型

1.1整车模型

文中建立了包括车辆的纵向运动、侧向运动、横摆运动以及前后车轮转动在内的整车五自由度模型，如图1所示，并做如下假设：①车辆模型的质心与车辆坐标系的原点重合；②悬架对车辆的垂直运动没有影响；③车辆没有俯仰和侧倾方向的自由度；④忽略纵向滚动阻力对状态参数的影响[9].

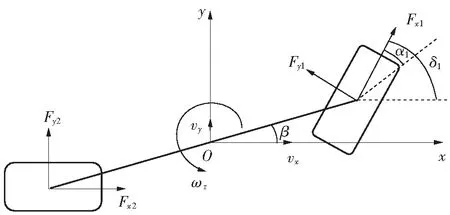
图1　整车模型

车身部分的动力学方程如下：

式中，m为车辆的总质量，Iz为车辆绕z轴旋转的转动惯量，δ1为车辆的前轮转向角，a、b分别为车辆质心到前、后车轮中心的距离，vx、vy分别为车辆的纵向、侧向速度，ωr为车辆的横摆角速度，Fx1、Fy1、Fx2、Fy2分别为前、后轮的纵向力和侧向力，Fw为车辆的空气阻力.

车轮转动的动力学方程如下：

(2)

式中，I1、I2分别为前、后车轮的转动惯量，ω1、ω2分别为前、后车轮的转速，Tt为驱动轮的驱动力矩，Tb为制动力矩，R1、R2分别为前、后车轮的滚动半径.

1.2轮胎模型

文中采用的Dugoff轮胎模型具有形式简单的优点，并且可以计算纯纵滑工况、纯侧偏工况和纵滑侧偏联合工况下的轮胎纵向力与侧向力，因而在车辆实时估算与仿真领域得到了广泛的应用[10].

Dugoff模型如下：

(3)

式中，Fx、Fy分别为轮胎的纵向力和侧向力，Cs、Cα分别为轮胎的纵向刚度和侧向刚度，

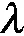
(4)

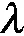
(5)

μmax为峰值路面附着系数，s为轮胎的纵向滑移(转)率，α为轮胎的侧偏角，α1和α2分别为前轮和后轮的侧偏角，

(6)

(7)

Fz为轮胎的垂向载荷，考虑到纵向轴荷转移对轮胎垂向载荷的影响，其计算公式为

(8)

g为重力加速度常数，hg为车辆质心距地面高度，L为车辆的轴距.

2　利用附着系数估计

2.1功能原理

功能原理的基本内容是系统的机械能增量等于外力对系统所作的总功与系统内部耗散力所做的功的代数和[11].对车辆来说，其系统内部耗散力主要指悬架阻尼器的阻尼力和系统内各处的摩擦力，这些力与轮胎和地面间的作用力相比都很小，故文中忽略这些系统内部耗散力所做的功，即认为车辆的动能变化量等于车辆受到的外力功的代数和.

2.2基于功能原理的利用附着系数估计

车辆纵向、侧向和绕z轴的动能变化量分别为

(9)

式中，vx、vx0、vy、vy0分别为车辆当前的纵向速度、侧向速度以及对应的初始速度，ωr、ωr0分别为车辆当前的横摆角速度和初始横摆角速度.

车辆在沿x、y、绕z轴方向受到的各个外力和外力矩所做的功分别为

(10)

式中，Sx、Sy分别为车辆在x和y轴上的位移，β为车辆的横摆角.

根据功能原理有

ΔEx+ΔEy+ΔEz=Wx+Wy+Wz

(11)

假设车辆的前、后轮正行驶在附着系数相同的路面上，则轮胎纵向力和侧向力与垂向力有如下关系：

(12)

式中：i=1，2分别代表前、后轮；μx、μy分别为纵向和侧向利用附着系数.

联立以上各式有

[μx,μy][Fz1(Sxcosδ1+Sysinδ1+aβsinδ1)+Fz2S，

Fz1(Sycosδ1-Sxsinδ1+aβcosδ1)+Fz2(Sy-bβ)]T

(13)

2.3递归最小二乘参数估计器的设计

式(13)可改写为标准的参数识别方程形式

y(k)=φT(k)θ(k)+e(k)

(14)

e(k)为估计误差.

(15)

3　峰值附着系数的估计

为了实现对路面峰值附着系数的估计，文中设计了一个Mamdani型的模糊控制器，该控制器以利用附着系数和车轮滑移(转)率为输入，通过与6条参考路面的比较，得到6种参考路面相似程度的权重系数xj(j=1，2，…，6)，进而计算当前行驶路面的峰值附着系数.

3.1参考路面的选择

参考Norrman划分机动车路面打滑的方法，根据我国典型地区的气候特点，将我国的公路路面状况分为以下7种类型：干燥路面、湿滑路面、积水路面、浮雪路面、积雪路面、泥泞湿滑路面、结冰路面[14].考虑到估计算法的实时性和我国路面材料，文中选用以下6种路面作为参考路面：干沥青、干水泥、湿沥青、湿鹅卵石、雪、冰.

根据半经验轮胎-路面数学模型[15]

μ(s)=C1(1-e-C2s)-C3s

(16)

得到6种路面的参数值(C1、C2、C3)[16]和峰值附着系数，如表1所示.

表1 参考路面的参数值及峰值附着系数

Table1Parametersandmaximumfrictioncoefficientofthereferenceroads

路面C1C2C3μmax干沥青1.280123.99000.52001.1700干水泥1.197325.16800.53731.0900湿沥青0.857033.82200.34700.8013湿鹅卵石0.400433.70800.12040.3400雪0.194694.12900.06460.1907冰0.0500306.39000.00000.0500

从表1可以看出，干沥青和干水泥的峰值附着系数比较接近.为提高对高附着系数路面估计的准确度，文中引入了一种虚拟的高附着路面来代替干沥青路面，该虚拟的高附着路面的峰值附着系数为1.4，其参数值分别为C1=1.5，C2=24，C3=0.45.

3.2模糊控制器的设计

文中将滑移(转)率划分为3个模糊子集，选用三角形函数作为隶属度函数，滑移(转)率的隶属度函数如图2所示.

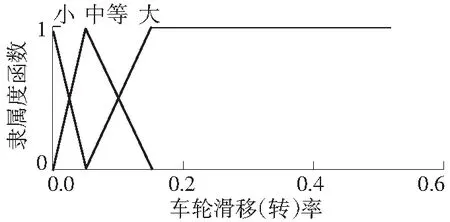
图2　滑移(转)率的隶属度函数

在滑移(转)率很小的情况下，各个参考路面的利用附着系数区别很小，难以区分各个路面，故当滑移(转)率为小时，系统不更新峰值附着系数的估计值，而是保持上一时刻的估计值输出；当滑移(转)率为中或大时，对利用附着系数进行模糊化，其隶属度函数如图3所示.

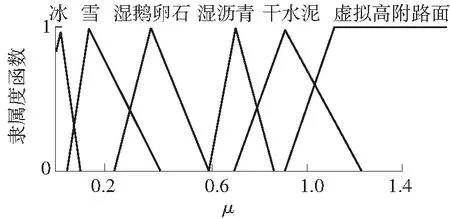
(a)滑移(转)率为中时

(b)滑移(转)率为大时

文中制定了如表2所示的12条模糊推理规则.其中，VD表示非常不相似，D表示不相似，GS表示一般相似，S表示相似，VS表示非常相似.

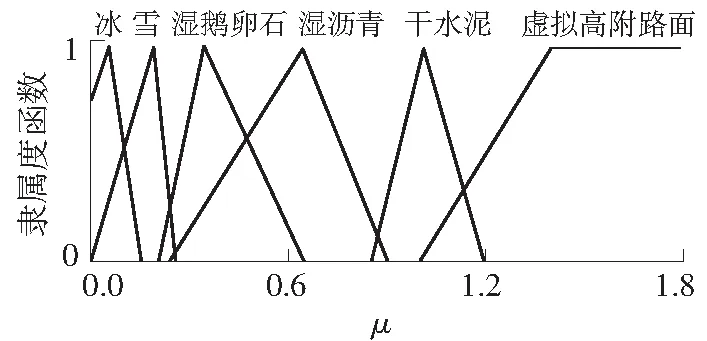
考虑到高斯型函数比三角形函数具有更好的区

分度，故文中采用高斯型函数作为隶属度函数，并采用中位数法进行清晰化处理.相应的清晰化模糊子集和隶属度函数如图4所示.

图4　清晰化模糊子集和隶属度函数

3.3峰值附着系数的计算

在得到6个参考路面的权重系数之后，计算路面峰值附着系数：

(17)

式中，μmax,j为第j种路面的峰值附着系数.

4　仿真验证

为验证文中算法的有效性和正确性，文中利用Simulink软件建立了整车模型，并对算法进行仿真验证.为了尽可能地覆盖典型路面和行驶状态，文中选择3种路面状态(峰值附着系数为0.85、0.55、

表2　 模糊规则

0.20)和2种行驶状态(驱动轮滑移(转)率为0.12、0.90)进行仿真验证

调整驱动轮的驱动力矩和制动力矩，使驱动轮的滑移(转)率为0.9，仿真结果如图5所示.从图中可以看到，估计结果在非常短的时间内就收敛到真实值附近，峰值附着系数，估计值的最大相对误差不超过5%，文中提出的算法在大滑移率情况下具有非常好的准确性与实时性.

(a)利用附着系数

(b)峰值附着系数

图5大滑移(转)率下利用附着系数和峰值附着系数的仿真结果

Fig.5Simulated results of utilized friction coefficient and maximum friction coefficient under large slip radio

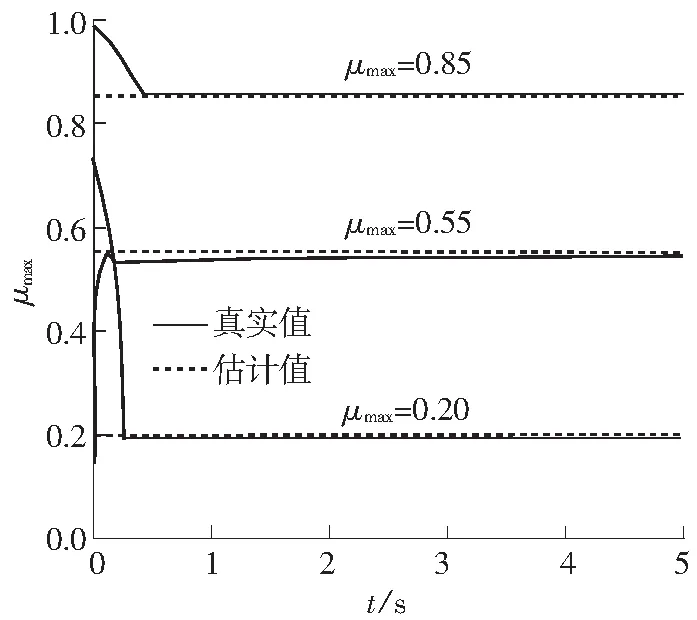
调整驱动轮的驱动力矩和制动力矩，使驱动轮的滑移(转)率为0.12，仿真结果如图6所示.从图中可以看到，在中等滑移率情况下，峰值附着系数的估计值可以在0.5s内收敛到真实值附近，并且其最大相对误差不超过5%，这表明文中提出的算法在中等滑移率条件下依然具有良好的准确性与实时性.

综上所述，无论行驶在何种路面上，只要轮胎滑移(转)率足够大，文中算法都可以准确地估计出峰值附着系数,估计值在0.5 s内即可收敛到真实值附

(a)利用附着系数

(b)峰值附着系数

图6中等滑移(转)率下利用附着系数和峰值附着系数的仿真结果

Fig.6Simulated results of utilized friction coefficient and maximum friction coefficient under medium slip radio

近，显示出良好的实时性，因此文中提出的算法兼顾了准确性和实时性.

5　结论

文中提出了一种基于功能原理和模糊控制的路面附着系数估计算法，得出如下结论：

(1)由于不引入轮胎模型，文中提出的路面附着系数估计算法的精度不受轮胎参数变化的影响；

(2)文中算法具有良好的适应性，对不同的路面而言，只要轮胎的滑移(转)率足够大，就可以获得可靠的估计结果；

(3)在各种情况下，路面附着系数估计值都可以在0.5 s内收敛到真实值附近，证明了文中算法具有良好的实时性；

(4)文中算法兼顾了准确性和实时性的要求，因而适用于车载系统.

[1]陈锦曦.基于容积卡尔曼滤波的路面附着系数估计算法研究 [D].成都：电子科技大学，2014.

[2]UMENOT.Estimationoftire-roadfrictionbytirerotatio-nalvibrationmodel[J].R&DReviewToyotaCRDL， 2002，37：53-58.

[3]UMENOT，ONOE，ASANOK，etal.Estimationoftire-roadfrictionusingtirevibrationmodel[R].Warrendale：SAEInternational，2002.

[4]CHENLong，BIANMingyuan，LUOYugong，etal.MaximumtireroadfrictionestimationbasedonmodifiedDugofftiremodel[C]∥Proceedingsof2013InternationalConfe-renceonMechanicalandAutomationEngineering.Jiujang：IEEE，2013：56-61.

[5]LIUCS，PENGH.Roadfrictioncoefficientestimationforvehiclepathprediction[J].VehicleSystemDynamics， 1996，25(S1)：413-425.

[6]胡丹.基于双扩展卡尔曼滤波的汽车状态及路面附着系数估计算法研究 [D].长春：吉林大学，2009.

[7]王丽.基于能量法的路面附着系数识别方法研究 [D].长春：吉林大学，2012.

[8]SONGXiang，LIXu，ZHANGWei-gong，etal.Approachtoestimationofvehicle-roadlongitudinalfrictioncoefficient[J].JournalofSoutheastUniversity(EnglishEdition)，2013，29(3)：310-315.

[9]李刚，解瑞春，卫绍元，等.基于双容积卡尔曼滤波的车辆状态与路面附着系数估计 [J].中国科学：技术科学，2015，45(4)：403-414.

LIGang，XIERui-chun，WEIShao-yuan，etal.VehiclestateandroadfrictioncoefficientestimationbasedondoublecubatureKalmanfilter[J].ScientiaSinicaTech-nologica，2015，45(4)：403-414.

[10]BIANMing-yuan，CHENLong，LUOYu-gong，etal.Adynamicmodelfortire/roadfrictionestimationundercombinedlongitudinal/lateralslipsituation[R].Warrendale：SAEInternational，2014.

[11]夏冰.基于功能原理的重型车质量辨识方法研究 [D].长春：吉林大学，2013.

[12]AOKIJ，MURAKAMIT.Amethodofroadconditionestimationandfeedbackutilizinghapticpedal[C]∥Proceedingsofthe10thIEEEInternationalWorkshoponAdvancedMotionControl.Trento：IEEE，2008：777-782.

[13]葛柱洪.基于CPN的四轮驱动车辆动力系统分析及驱动控制 [D].哈尔滨：哈尔滨工业大学，2013.

[14]周须文.气象条件对高速公路路面抗滑性能的影响及预报探讨 [C]∥中国气象学会2007 年年会气象软科学论坛分会场论文集.广州：中国气象学会，2007.

[15]BURCKHARDTM，REIMPELLJörnsen.Fahrwerktechnik：radschlupf-regelsysteme[M].Wrzburg：Vogel-Verlag，1993.

[16]刘国福，张玘，王跃科，等.一种基于模型的最佳滑移率计算方法 [J].公路交通科技，2004，21(7)：111-114.

LIUGuo-fu，ZHANGQi，WANGYue-ke，etal.Studyofcalculationofmodelbasedoptimalslipratio[J].JournalofHighwayandTransportationResearchandDevelopment，2004：21(7)：111-114.

SupportedbytheNationalNaturalScienceFoundationofChina(51505179)

EstimationofRoadAdhesionCoefficientBasedonWork-EnergyPrincipleandFuzzyLogicControl

LIN Bo-zongLI Zhen-yangHE LeiZONG Chang-fu

(StateKeyLaboratoryofAutomotiveSimulationandControl，JilinUniversity，Changchun130022，Jilin，China)

Inordertoavoidtheeffectsoftireparametersonestimationaccuracy,thetiremodelsarenotintroducedinthispaper.Onthisbasis,aroadadhesioncoefficientestimationalgorithmcombiningthework-energyprincipleandthefuzzylogiccontrolisproposed.First,theutilizedadhesioncoefficientundercurrentvehiclestateisestimatedonthebasisofthework-energyprinciple.Then,byusingafuzzylogiccontroller,themaximumadhesioncoefficientofcurrentroadisestimatedaccordingtoboththeutilizedadhesioncoefficientandtheslipratiounderthecurrentstate.Finally,byemployingtheMatlabsoftware,avehiclemodelofthreedegreesoffreedomisconstructedtoanalyzetheproposedalgorithmbysimulations.Theresultsshowthattheproposedalgorithmcaneffectivelyestimatetheroadadhesioncoefficient,andhasgoodreal-timeandaccuracy.

work-energyprinciple;fuzzylogic;roadadhesioncoefficient;estimationalgorithm

1000-565X(2016)09-0131-06

2015-08-04

国家自然科学基金资助项目(51505179)

林柏忠(1965-)，男，博士，副教授，主要从事汽车动力学仿真与控制研究.E-mail：672274352@qq.com

何磊(1982-)，男，博士，副教授，主要从事汽车动力学仿真与控制研究.E-mail：jlu_helei@126.com

U461.5

10.3969/j.issn.1000-565X.2016.09.019