尾矿坝溃决泥浆运动机制及其预测模型研究*
2016-10-28郑欣许开立徐晓虎
郑欣 许开立 徐晓虎
(东北大学资源与土木工程学院 沈阳 110819)
尾矿坝溃决泥浆运动机制及其预测模型研究*
郑欣许开立徐晓虎
(东北大学资源与土木工程学院沈阳 110819)
以尾矿溃坝砂流下游演进动力学过程为研究重点,综合运用水文学及水动力学等运动理论和数值计算方法,建立描述尾矿坝溃决泥浆运动的数学模型,采用VOF模型对溃坝后的砂流运动过程进行数值模拟。以某溃决尾矿坝为例,对溃坝后下泄砂流演进过程进行模拟,模拟得到的最终影响范围及泥深均与该溃决尾矿坝溃后的现场观测结果相吻合,证明了模拟的有效性和正确性。
尾矿坝溃坝运动机制影响区域预测
0 引言
尾矿库是维持矿山生产的重要设施,是金属与非金属矿山的重大危险源之一。国内外学者对尾矿库的研究主要集中于坝体安全与环境安全两个方面[1-5]。国外很多尾矿坝下游均为空旷的无人区,这也是国外学者很少研究溃坝后人员和财产损失的主要原因。我国不同于其他国家,尾矿库数量多、规模小,部分尾矿库安全管理不够规范,相当数量的尾矿坝下游就是密集的居民居住区,一旦溃坝可能引起大量的生命伤亡。对尾矿坝稳定性进行研究,防止溃坝事故的发生,是保证尾矿坝下游居民生命安全的重要手段,但也不可忽视对溃坝后果及事故应急救援的研究。对溃坝事故后果进行估算,首先需要明确尾矿溃坝砂流在坝体下游的运动规律,建立泥石流类下泄流体本构模型,预测尾矿溃坝后可能的影响范围,是减灾防灾工程和进行尾矿库风险管理的必要手段。
1 尾矿溃坝砂流流动模拟研究现状分析
尾矿库溃坝砂流演进模拟,主要是研究砂流在尾矿坝下游的推进过程、最终可能的影响范围以及不同时间、不同地点尾矿砂流的覆盖深度和流速。由于尾矿砂流与泥石流中的泥流相似,通常把尾矿砂流看作是宾汉流体,借鉴泥石流的研究方法进行研究。王又武等[6]按照尾矿坝全面溃决和局部溃决分别提出了溃坝水利计算公式;郭朝阳等[7]对原有泥石流以及水库溃坝等方面的数学模型进行适当的调整,建立尾矿溃坝泥石流数学模型,计算溃坝砂流冲击范围和破坏能力;陈殿强等[8]利用黄河水利委员会推出的经验公式,对某铁矿尾矿坝溃坝砂流下游演进进行了计算分析,得到了溃坝砂流的最终影响范围、最大砂流量、不同时间不同地点的尾矿砂流深度;林江、张绪进等[9]为模拟尾矿库溃坝稀性泥石流的演进,在溃坝洪水控制方程的基础上,加入非恒定流输沙方程,建立能同时模拟水流和泥沙运动的平面二维溃坝水流泥沙控制方程,最后将该模型应用于云南某尾矿坝溃坝后的洪水演进及矿砂在下游的淤积过程。李全明等[10]以尾矿坝溃坝砂流下游演进动力学过程作为研究的主要内容,运用水文学、水动力学及数值计算方法得到尾矿溃坝淹没范围的定量评估方法。目前尾矿坝溃坝砂流控制方程的数值求解方法有很多,其中有限体积法在国外研究较早,且较为完善[11-12]。
本文对溃坝砂流演进过程使用Fluent软件进行了两相流三维模拟,物理模型的建立和网格的划分均使用ICEM CFD,求解方法选取SIMPLE算法。
2 尾矿坝溃坝砂流演进模拟
2.1控制方程
尾矿溃坝产生的水与尾矿砂本质上属于泥石流,只是与一般的泥石流在组成上存在很大的差异性,可以参考泥石流的运动规律来进行尾矿溃坝砂流演进过程的研究。一般情况把大于某临界粒径(>2 mm)的粗泥沙或石块看作“固相”,把水和细颗粒泥沙结合而成的非沉降性浆体看作“液相”,由于尾矿砂粒径小,大部分粒径小于2 mm,故可把尾矿砂流看作是“液相”一相流。可以把溃坝后尾矿砂流在尾矿坝下游的演进过程当作气液两相流进行模拟。多相流可以分为气固两相流、气液两相流、液液两相流、固液两相流等。工业应用和自然界中最常见的是气液两相流,如何追踪动态相间的自由界面是气液两相流数值模拟中的一个关键性问题。由Hirt和Nichols提出[13]的VOF方法,能够比较有效地处理自由表面的追踪问题,本文将采用该方法处理自由表面。
VOF方法对每一项引入体积分数,通过求解每一控制单元内的体积分数,确定相间界面。在每一个控制体中,所有的相体积分数之和为1。公式(1)为体积函数的控制方程。
(1)
其中,aq为第q相流体积函数,无量纲;ui为速度分量,m/s;xi为坐标分量,m;Saq为q相的质量源,无源情况下为零。
以Navier-Stokes方程为基础, 紊流方程为封闭模型,建立溃坝砂流运动过程三维数学模型。动量方程、连续方程、紊动能方程和紊动能耗散率方程等基本微分方程如下所示。
连续方程:
(2)
动量方程:
(3)
K方程:
(4)
ε方程:
(5)
式中,t为时间,s;ui,uj为速度分量,m/s;xi,xj为坐标分量,m;ρ为流体密度,kg/m3;μ为分子黏性系数,(N·m)/s;k为紊动动能,m2/s2;ε为紊动耗散率,m2/s2;P为修正压力,Pa;C1ε,C2ε为经验常数,无因次。
在引入体积函数后,密度ρ和黏性系数μ不再是常量,而是与体积函数有关的量,其表达式如下:
ρ=awρw+(1-αw)ρa
(6)
μ=αwμw+(1-αw)μa
(7)
式中,ρw,ρa为水、气2种流体的密度,kg/m3;αw为水的体积分数,无因次;μw,μa为水、气2种流体的分子动力粘性系数,(N·m)/s。
2.2网格划分及边界条件的设置
ICEMCFD是美国ICEMTechnologies公司的产品,于1990年问世,2000年被ANSYS公司收购。ICEMCFD几何模型工具能清理建模过程中形成的不完整曲面,高度智能化的ICEMCFD软件拥有强大的CAD模型修复能力、自动中面抽取、独特的网格“雕塑”技术,可生成结构化网格、非结构化网格、适体坐标以及H型自适应网格。本文模拟的前处理阶段主要建模和网格划分均使用的是ICEMCFD,流场区域网格采用的是非结构化网格。
Fluent的边界条件包括:
(1)流动进、出口边界条件;
(2)壁面、轴对称和周期性边界;
(3)Internalcellzones:fluid,solid(porousisatypeoffluidzone);
(4)Internalfaceboundaries:fan,radiator,porousjump,wall,interior。
本文模拟边界条件设置如下:所有壁面和底面设置为Wall,所有和空气接触的面设置为压力出口,初始压力为大气压。
3 溃坝砂流演进模拟对比研究
以金山尾矿库为例,该尾矿库于1980年启用,为了满足生产澄清回水的要求,尾矿库经常处于高水位状态。初期土坝高6m,尾矿堆积坝(包括子坝在内)总高达21.7m,库区纵深径流距离为150m。1986年4月30日凌晨该尾矿坝中段发生溃决事故。事故发生后对现场进行调查取证,库内水及尾矿总量为84.5 万m3,绝大部分倾斜下游,坝顶决口宽度为245m。溃决剧滑下泄过程历时几分钟,现场取得的数据如下:密度为1.6t/m3,糙率系数n为0.06,下游堆积区坡度为零,坝的内坡比为1.0∶1.6,外坡比为1.0∶2.0。根据现场调查,溃坝下泄砂流总量为84万m3,全六面体网格划分,总共有600 438个网格。
坝址流量过程线如图1所示。
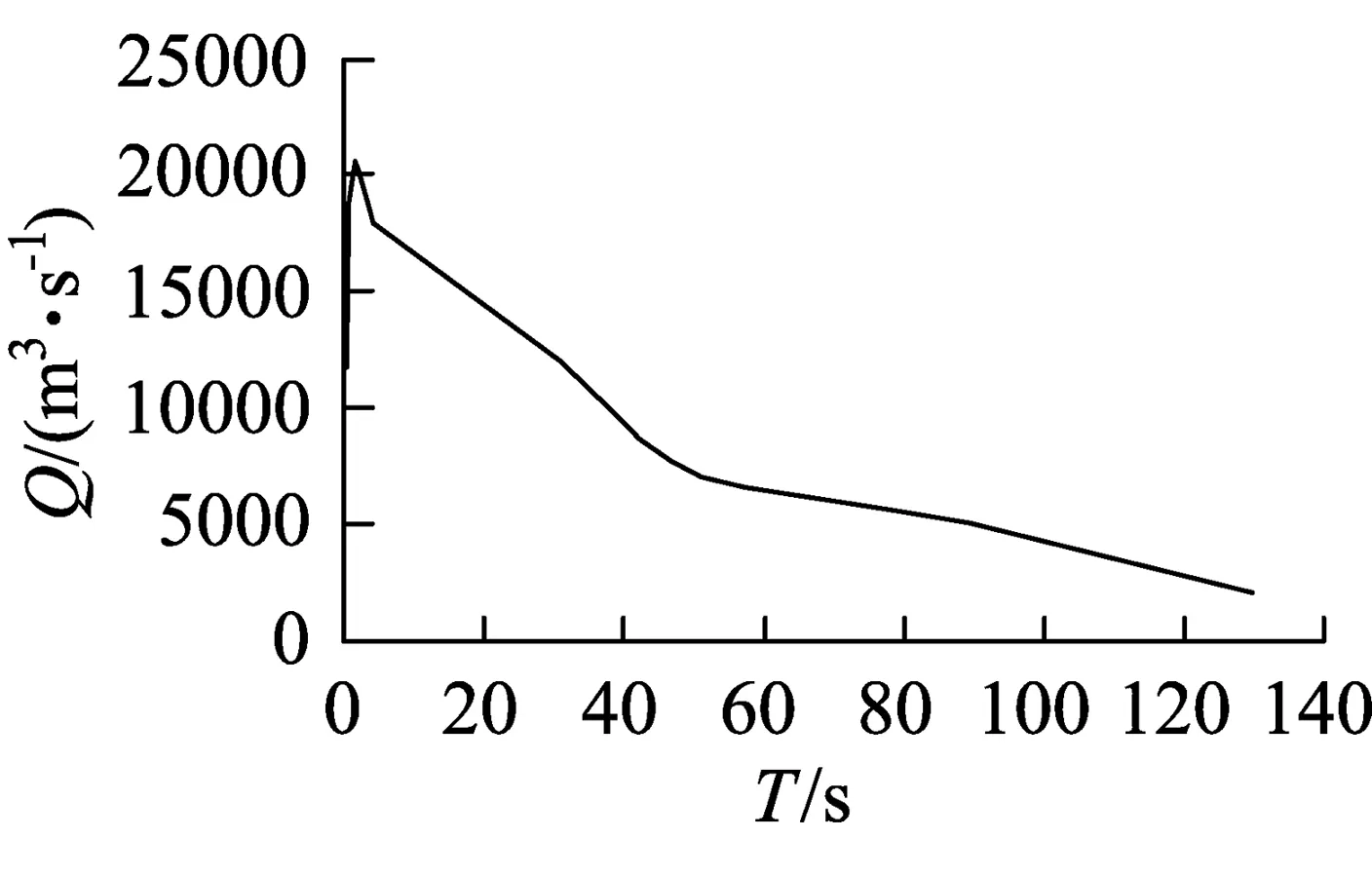
图1 下泄砂流过程线
砂流最终影响范围的对比图如图2,其中虚线部分为真实的影响范围。不同时刻尾矿砂流影响范围见图3。不同时刻溃坝后下游的泥深情况见图4。溃坝后下游不同位置不同时间的速度情况见图5。
溃坝尾矿砂在坝下游逐渐形成一个“涌波”并向下游传播。根据溃坝现场实际测量,近坝址处尾矿砂的最终覆盖厚度约为1.8m,距坝址1 000m的下游最终覆盖厚度约0.5m。将本文模拟结果与溃坝后现场观测结果进行对比可以看出,模拟得出的最终影响范围及泥深情况与实际基本吻合。

图2 砂流最终影响范围
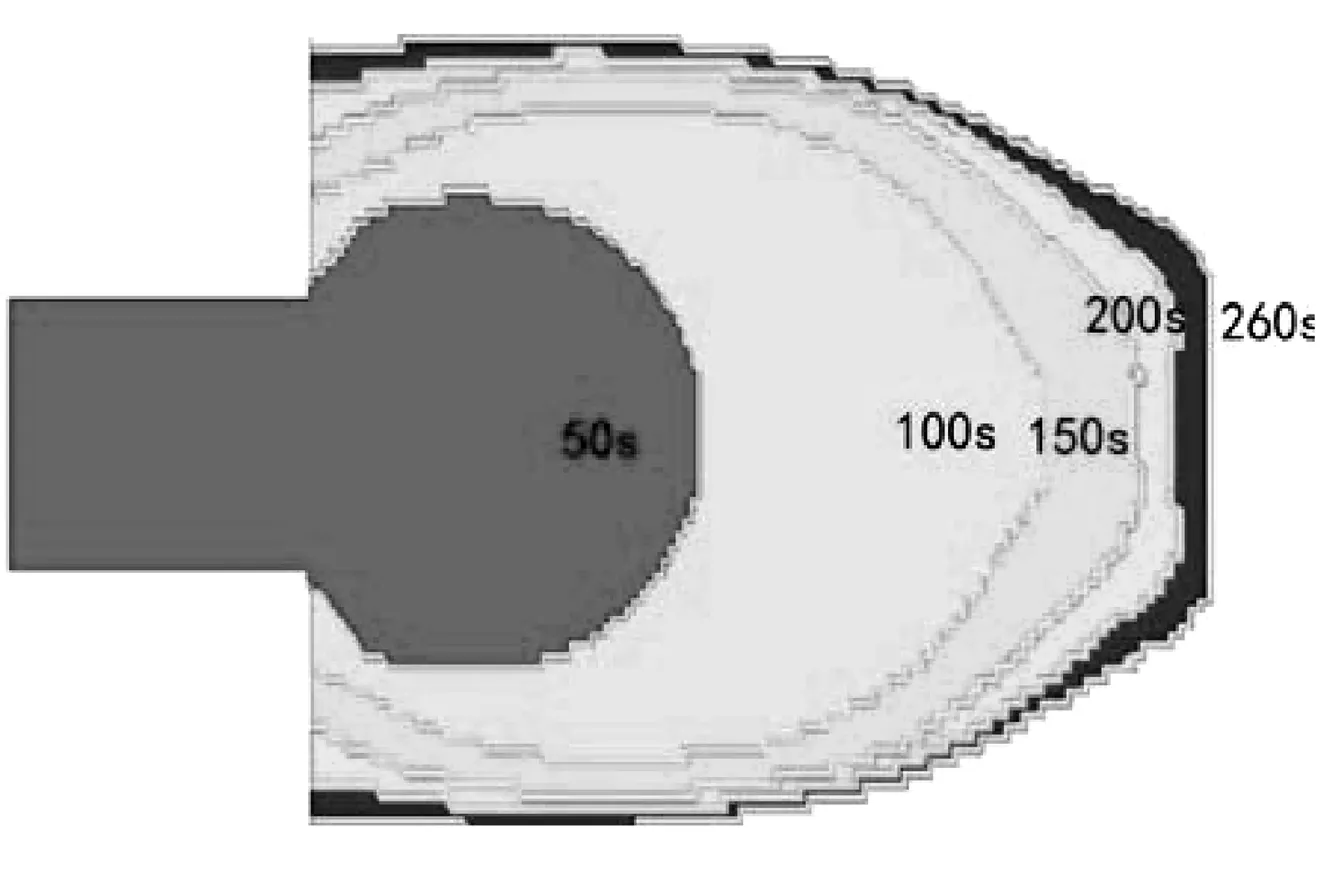
图3 不同时刻砂流影响范围

图4 不同时刻溃坝后下游的泥深情况

图5 不同位置不同时间的速度情况
4 结论
(1)由于尾矿砂粒径小,故可把尾矿砂流看作是液相“一相流”,把下泄砂流的演进过程按气液两相流进行模拟。数学模型以Navier-Stokes方程为基础,物理模型的建立和网格的划分均使用ICEMCFD,求解方法选取SIMPLE算法,紊流方程为封闭模型,自由表面的追踪采用VOF法,使用Fluent软件对溃坝砂流演进进行三维模拟。
(2)以曾经发生过溃坝的金山尾矿库为例,对溃坝后下泄砂流演进行模拟,得到的最终影响范围及几个点处的泥深均与现场观测结果比较吻合,证明了模拟的有效性和正确性。
(3)尾矿坝溃坝风险的大小,由事故发生的可能性和事故后果的严重性两方面来决定,不仅应关注坝体稳定性方面的研究,更应该强化溃坝后事故后果估算和事故应急决策方面的研究。对尾矿坝溃坝风险进行系统科学的评估,可为国家尾矿库风险管理提供依据。
[1]MariaTZandarin.Theroleofcapillarywaterinthestabilityoftailingdams[J].EngineeringGeology,2009,105(1/2):108-118.
[2]M Rico. Floods from tailings dam failures[J].Hazardous Materials,2008,154(1/2/3):79-87.
[3]Stephen R Griffiths. Factors in fluencing the risk of wild life cyanide poisoning on a tailing storage facility in the Eastern Gold fields of Australia[J].Ecotoxicology and Environmental Safety,2009,72(5):1579-1586.[4]M Rico. Reported tailings dam failures a review of the European incidents in the worldwide context[J].Hazardous Materials, 2008,152(2):846-852.
[5]Jason Phillips. Applying a mathematical model of sustainability to the rapid impact assessment matrix evaluation of the coal mining tailings dumps in the Jiuliu Valley, Romania[J].Resources, Conservation and Recycling,2012,63(8):17-25.
[6]王又武,袁平,陈坷佳,等.尾矿库溃坝有关问题探讨[J].工程建设,2008,41(5):35-41.
[7]郭朝阳,唐治亚.尾矿库溃坝模型探讨[J].中国安全生产科学技术,2010,6(1):43-47.
[8]陈殿强,何峰,王来贵.凤城市某尾矿库溃坝数值计算[J].金属矿山,2009 (10):74-77.
[9]林江,张绪进,张小峰.考虑矿砂淤积的尾矿坝溃坝洪水数值模拟[J].中国农村水利水电,2009(5):150-153.
[10]李全明,李玲,王云海,等.尾矿库溃坝淹没范围的定量计算方法研究[J].中国安全科学学报,2011(11):92-96.
[11]LEVEQUE R J. Finite volume methods for hyperbolic problems [M].Cambridge: Cambridge University Press,2002.
[12]TORO E F. Shock-capturing methods for free-surface shallow flows[M]. Chichester: John Wily&Sons,2001.
[13]Hirt C W,Nichols B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics,1981,39(1):201-225.
Research on Movement Mechanism of Tailings Flow and Calculating Method of Submerged Area
ZHENG XinXU KailiXU Xiaohu
(SchoolofResources&CivilEngineering,NortheasternUniversityShenyang110819)
Focused on the study of the dynamics process of tailings flow in the down- stream, a mathematical model describing the tailings dam break flow movement is systematically established from hydrology, water dynamics and motion theory, and then the tailings flow movement process is simulated by using VOF model. Taking one broken tailings dam as an example, the tailings dam-break flow’s evolution process is simulated. The simulation result basically agrees well with the measured value from ultimate impact range and depth of the tailings dam mud, which proves the simulation to be valid and correct.
tailings damdam breakmovement mechanisminfluence areaestimation
国家自然科学基金(51404063)。
郑欣,女,1978年生,辽宁本溪人,东北大学讲师,博士。
2015-08-25)
许开立,男,1965年生,山东郓城人,东北大学教授。
