海上丛式井组钻井顺序优化模型及求解方法
2016-10-28曹向峰管志川史玉才
曹向峰, 管志川, 史玉才, 薛 磊, 张 欣
(1.中国石油大学石油工程学院,山东青岛 266580; 2.中石化胜利石油工程有限公司钻井工艺研究院,山东东营 257017;3.中海油安全技术服务有限公司,天津 300452)
海上丛式井组钻井顺序优化模型及求解方法
曹向峰1,2, 管志川1, 史玉才1, 薛磊1, 张欣3
(1.中国石油大学石油工程学院,山东青岛 266580; 2.中石化胜利石油工程有限公司钻井工艺研究院,山东东营 257017;3.中海油安全技术服务有限公司,天津 300452)
海上丛式井组待钻井较多且井口间距较小,优化钻井顺序有助于防碰和采用批钻井方式。综合考虑防碰要求并兼顾批钻井要求,以井眼分离系数作为井眼交碰风险评价指标,以整个井组的防碰井段总长度最小作为钻井顺序优化目标,建立海上丛式井组钻井顺序优化模型及遗传算法求解方法,给出实例计算分析。结果表明:以整个井组的防碰井段总长度最小作为海上丛式井组钻井顺序优化指标是可行的;建立的钻井顺序优化方法能够满足海上丛式井防碰及批钻井要求。
海上丛式井; 钻井顺序; 优化模型; 防碰; 批钻井; 遗传算法
引用格式:曹向峰,管志川,史玉才,等.海上丛式井组钻井顺序优化模型及求解方法[J].中国石油大学学报(自然科学版),2016,40(3):96-101.
CAO Xiangfeng, GUAN Zhichuan, SHI Yucai, et al. Drilling sequence optimization model and its solution method for offshore cluster wells[J]. Journal of China University of Petroleum (Edition of Natural Science), 2016,40(3):96-101.
海上丛式井组待钻井较多且井口间距较小,考虑防碰要求时通常先钻外围水平位移大、造斜点浅的井,后钻内排水平位移小、造斜点深的井[1-6];考虑批钻井要求时通常采用跳“日”字或“田”字的斜对角线钻井顺序[2]等。笔者以防碰为优化目标,兼顾批钻井要求,建立海上丛式井组钻井顺序优化的数学规划模型及遗传算法求解方法。
1 海上丛式井组钻井顺序优化模型
防碰问题贯穿丛式井组钻井设计及施工全过程。考虑到海上丛式井防碰问题的重要性,优选钻井顺序时应首先考虑防碰要求,其次才是批钻井要求。
1.1选择钻井顺序优化指标
井眼交碰风险评价指标包括邻井最近距离[3,6]、井眼分离系数[7-9]、井眼交碰概率等[7,10-11]。其中,邻井最近距离未考虑井眼轨迹误差影响,评价结果不够可靠;其余指标均考虑了井眼轨迹误差影响,评价结果比较可靠。选择井眼分离系数作为井眼交碰风险评价指标,并基于井眼交碰风险分析结果构建钻井顺序优化指标。
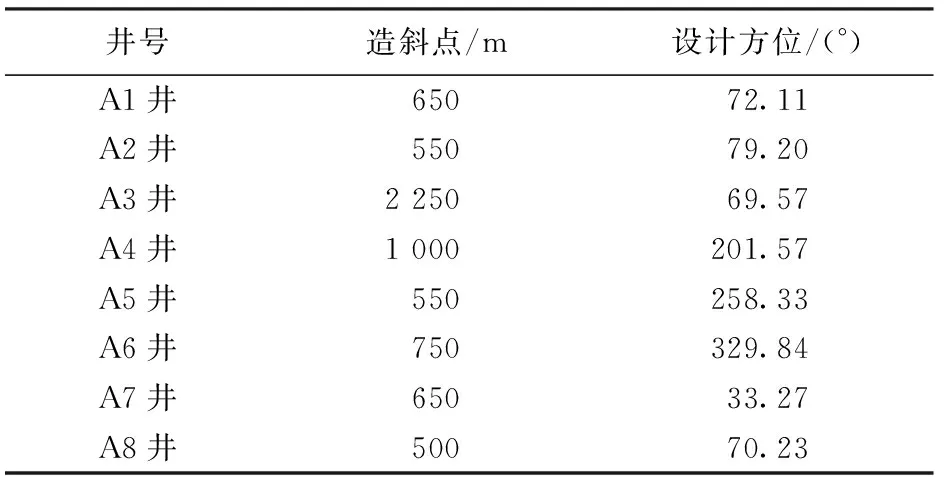
井眼分离系数越小,井眼交碰风险越高,防碰难度也较大。钻井现场依据井眼分离系数划分了井眼交碰风险等级,制定了相应的防碰技术规范[12-14]。例如,当分离系数SF>5.0时可以安全钻进;1.5 当丛式井组的井眼轨道设计工作完成之后,整个井组的防碰井段总长度与钻井顺序有关。反之,可以用防碰井段总长度最小为优化指标,优化海上丛式井钻井顺序。 以A6井、A7井、A8井为例,井眼交碰风险分析结果见表1。其中,若同一口井与多口邻井的防碰井段有重叠部分,统计该井的防碰井段长度时重叠部分不得重复计入。比如,最后钻A8井时需要同时与A6井和A7井防碰,防碰井段分别为501~508、501~552 m,扣除重叠井段之后,钻A8井时防碰井段应为501~552 m、长度为52 m。可以看出,对于A6井、A7井、A8井来说,钻井顺序A6→A8→A7和A8→A6→A7对应的防碰井段总长度最小,均为217 m;钻井顺序A7→A8→A6和A8→A7→A6对应的防碰井段总长度最大,均为253 m,比最小值多了36 m(16.59%)。依据现有的钻井顺序优化原则,可以判断出钻井顺序A8→A6→A7和A6→A8→A7满足防碰及批钻井要求,而钻井顺序A7→A8→A6和A8→A7→A6不满足防碰及批钻井要求。 表1 钻井顺序与防碰井段总长度 1.2构建钻井顺序优化目标矩阵 需要先完成整个井组的井眼交碰风险分析工作,再构建钻井顺序优化对应的目标矩阵。 (1)最近距离扫描分析。将全部设计轨道转换到同一个坐标系中,应用等间距插值法求出各设计轨道上插入点的坐标[15],再结合文献[16]给出的最近距离防碰扫描方法,对任意两口井进行最近距离防碰扫描分析,计算出基准点到邻井的最近距离及对应井深。 (2)井眼轨迹误差分析。将设计轨道视为实钻轨迹,并按钻井设计给定的轨迹测量方式选择测量误差,然后应用现有的井眼轨迹误差分析方法[17],计算出各井设计轨道上全部插值点对应的误差椭球参数。 由于设计井眼轨道造斜点以上通常为垂直井段,方位角不确定,误差椭球的空间姿态也不确定,若人为指定某个方位角就相当于指定了误差椭球的空间姿态,会影响井眼交碰分析结果。尝试采用过多种处理方法,发现将上部垂直井段误差椭圆等效成面积相等的误差圆是比较合适的。 (3)井眼交碰风险分析。井眼分离系数有多种计算方法,包括传统方法[14]、中心向量法[7]、等效椭球法[18](定向分离系数)、垂足线法[7]、椭圆缩放法[19]等。选择不同的计算方法,井眼分离系数计算结果也不同,有可能过于乐观,也有可能过于保守。 综合考虑计算难度及钻井现场认可度,采用中心向量法计算各待钻井设计轨道上全部插值点对应的井眼分离系数。 (4)构建钻井顺序优选目标矩阵。基于井眼交碰风险分析结果,将各个设计轨道上井眼分离系数小于1.5的所有插值点编号分别存放到集合Sij和Sji(i,j=1,2,…,n)中,最终整理出目标矩阵。 (1) 目标矩阵S中每个元素都是一个子集合,集合Sij和Sji不一定相同;因为集合Sij是以i井为基准井,以j井为比较井时,i井设计轨道上分离系数小于规定值的全部节点编号;Sji是以j井为基准井,以i井为比较井时,j井设计轨道上分离系数小于规定值的全部节点编号;当i=j时集合Sij=φ(空集)。 1.3建立钻井顺序优化模型 对n口井从1至n进行编号,用编号代替井号,每一种钻井顺序都对应一个具有n个元素的全排列。设全排列P为任一种钻井顺序,即P=[p1,p2,…,pk,…,pn],k=1,2,…,n;1≤pk≤n。以整个井组的防碰井段总长度最小为优化目标建立钻井顺序优化模型: (2) 上述海上丛式井钻井顺序优化模型尚未考虑油藏开发方案调整以及批钻井要求。为了弥补该缺陷,可以利用上述模型求出多个备选方案(包括若干个最优解及次优解),再综合考虑油藏开发方案和批钻井要求,进行适当调整。 此外,考虑到丛式井防碰井段往往不限于同一个开次,造斜点深度(直井段长度)和井眼尺寸也影响井眼交碰风险评价结果及防碰施工效果,采用批钻井方式时建议分开次建立和求解丛式井施工顺序优化模型;不采用批钻井方式则可以直接采用该优化模型,在多个备选方案之中需要防碰的井眼长度之和越小越好。 理论上说,n口井的钻井顺序有n!种。当待钻井较多时,适合采用遗传算法[20]求解钻井顺序优化问题,也就是寻找某一个(或多个)钻井顺序使整个井组的防碰井段总长度最小。 采用遗传算法[20]求解本文建立的钻井顺序优化模型时,推荐按以下方法选择初始群体和迭代次数、构造适应度函数和优化遗传算子(包括选择算法、交叉算法、变异算法)。 (1)初始群体。对于n口井随机产生N组序列个体,作为初始群体。选择不同井数进行试算,统计分析发现取初始群体N=4n时,得到最优解的概率比较大且迭代时间不会过多。 (2)适应度函数。式(2)给出的钻井顺序优化问题属于最小值问题,应用遗传算法求解该问题时,需要构造适应度函数: (3) 式中,f(i)为初始群体中第i个个体对应的适应值;L(i)为第i个个体对应的防碰井段总长度,m;Lmax和Lmin分别为初始群体中防碰井段总长度的最大值和最小值,m。 由式(3)看出,适应度函数的值域为(0,1),防碰井段越小则适应度越大。 (3)选择算法。采用比例选择方法选择初始群体[21]。预先生成一个0到1的随机值,若被选择的个体的适应值大于该随机值,就将该个体放入交配池中。 (4)交叉算法。每一种钻井顺序都对应一个具有n个元素的全排列,最适合采用部分映射交叉方法[21,22]。为避免父代交叉产生较差的子代,还需要加入交叉检验步骤: ①根据井数n,按式(4)确定交叉带的宽度w,然后随机选取交叉带的起始位置, (4) ②交换双亲的交叉带,形成原始子代; ③确定两交叉带的映射关系; ④根据映射关系,对原始子代的非交叉带进行变化,直到子代没有冲突。 (5)变异算法。变异算子能改变个体的某些基因,产生新的个体,增强种群的多样性,能有效地避免较早收敛而产生局部最优解的现象(早熟)[23-24]。 钻井顺序优化问题适合采用互换变异方法。也即,对某一钻井顺序随机选择两个位置,然后将这两个位置上的井号进行相互交换。为了避免早熟现象,进行强制群体变异,并加入变异检验步骤防止变异产生较差子代。 (6)迭代次数。迭代次数并非越多越好,因为当迭代次数增加到一定值时,有可能已经找到全局最优解或次优解,过多的迭代只会增加程序运行时间。目前主要根据经验或试算方法确定迭代次数。据试算结果,推荐按下式确定迭代次数: (5) 式中,n为丛式井组井数;C为迭代次数。 (7)其他注意事项。建立的丛式井钻井顺序优化模型通常会出现多解现象。为了找到全部最优解(或次优解),可对遗传算法重复运行约10次,并且每次都重置初始群体,最后输出多个钻井顺序,以便钻井设计人员结合批钻井要求做进一步筛选。 此外,模拟计算分析还发现,当丛式井井数不超过20口时,遗传算法能求出最优解;当井数超过20口时,也能求出比较好的近似解,基本上能够解决上百口井的钻井顺序优化问题。 以南海西部某海上丛式井组为例。该井组有8口定向井,设计方位及造斜点(KOP)见表1,井口槽排列关系见图1(间距2.28 m)。 表1 设计方位及造斜点 图1 井口槽排列关系Fig.1 Arrangement of slots 按钻井工程设计书中给定的轨道设计方案,取防碰扫描间距ΔL=1 m,按前文给出的方法建立海上丛式井钻井顺序优选数学模型并采用遗传算法求解(取初始群体N=32,交叉带宽度w=3,迭代次数C=100),计算结果如下: 按防碰井段总长度由小到大,列出部分最优解和次优解及其对应的防碰井段总长度。 此外,还计算出该井组防碰井段总长度最大值为1 462 m,比推荐钻井顺序多431 m(41.80%),与之对应的钻井顺序至少有以下几种: P1=[3,1,7,2,8,6,5,4],1 462m, P2=[3,1,7,8,6,2,4,5],1 462m, P3=[3,1,2,4,7,8,6,5],1 462m, P4=[1,2,3,7,8,4,6,5],1 462m, P5=[1,2,3,7,8,6,4,5],1 462m. 可以看出,上述几种钻井顺序均难以满足防碰和批钻井要求。比如,A3井位于井组中心且造斜点最深(2 250m),按丛式井防碰施工原则理应最后钻该井,若先钻该井势必导致整个井组的防碰井段总长度比较大,也难以满足批钻井要求(至少有2次需要将钻机移至相邻井口槽)。 此外,原钻井工程设计给出的钻井顺序为[8,5,2,7,1,6,4,3],也即A8→A5→A2→A7 →A1→A6→A4→A3,求出与之对应的防碰井段总长度为1 156m,比推荐钻井顺序多了125m(12.12%)。同时还发现,该钻井顺序尚未完全满足批钻井要求(有1次需要将钻机移至相邻井口槽)。 分析表明,笔者建立的海上丛式井钻井顺序优化方法更有优势,可明显减少海上丛式井组防碰井段长度,减少防碰施工难度和工作量,也有助于实现批钻井方式。 选择分离系数作为井眼交碰风险评价指标,以井组间防碰井段总长度最小为优化指标,建立了海上丛式井组钻井顺序优化模型。该模型可用遗传算法求解,能够满足海上丛式井防碰及批钻井要求。 [1]刘晓艳,施亚楠,李培丽. 丛式井组总体防碰与钻井顺序优化技术及应用[J]. 石油钻采工艺,2012,34(2):9-12,16. LIUXiaoyan,SHIYanan,LIPeili.Techniquesofclusterwellgeneralanti-collisionanddrillingsequenceoptimization[J].OilDrilling&ProductionTechnology, 2012,34(2):9-12, 16. [2]董星亮.海洋钻井手册[M].北京:石油工业出版社,2009. [3]中国石油天然气股份有限公司.密集丛式井上部井段防碰设计与施工技术规范:QSY1296-2010[S].北京:石油工业出版社,2010. [4]罗玉金,汪兴华,周永福.丛式井的优快钻井技术[J].重庆科技学院学报(自然科学版),2007,9(3):7-11. LUO Yujin,WANG Xinghua, ZHOU Yongfu. Optimized drilling technology of cluster well[J].Journal of Chongqing University of Science and Technology(Natural Science Edition), 2007,9(3):7-11. [5]韩雪银,付建民,钟帆,等.丛式井防碰技术在金县1-1油田的应用[J].中国海上油气,2014,26(5):70-75. HAN Xueyin, FU Jianmin, ZHONG Fan, et al. Application of anti-collision solution for cluster wells in JXl-1 Oilfield[J]. China Offshore Oil and Gas, 2014,26(5):70-75. [6]石油钻井工程专业标准化委员会. 钻井井眼防碰技术要求:SY/T 6396-2009[S].北京:国家能源局,2009. [7]University of the Highlands and Islands, UHI Research Office. Introduction to wellbore positioning[EB/OL]. [2014-01-05]. http://www.uhi.ac.uk/en/research-enterprise/energy/wellbore-positioning-download. [8]POEDJONO B, AKINNIRANYE G, CONRAN G, et al. Minimizing the risk of well collisions in land and offshore drilling[R]. SPE 108279, 2007. [9]POEDJONO B, LOMBARDO G J, PHILLIPS W. Anti-collision risk management standard for well placement[R]. SPE 121040, 2009. [10]BROOKS A G. A new look at wellbore collision probability [R]. SPE 116155, 2010. [11]柳贡慧,董本京,高德利. 误差椭球(圆)及井眼交碰概率分析[J]. 钻采工艺,2000,23(3):5-12. LIU Gonghui, DONG Benjing, GAO Deli. Probability analysis of error ellipsoid(ellipse) and hole intersection [J]. Drilling & Production Technology, 2000,23(3):5-12. [12]POEDJONO B, AVILA C, VAN C P, et al. Case studies in the application of an effective anticollision risk management standard[R]. SPE 126722, 2010. [13]POEDJONO B, AKINNIRANYE G, CONRAN G, et al. Well-collision risk in congested environments[R]. SPE 101719, 2006. [14]CHENG Kun, CHENG Zhong, WEI Yunan, et al. China offshore anti-collision risk management standard and remedial measures[R]. SPE 141089, 2011. [15]韩志勇. 定向钻井设计与计算[M]. 2版. 东营:中国石油大学出版社,2007. [16]鲁港,邢玉德,吴俊林,等. 邻井防碰计算的快速扫描算法[J]. 石油地质与工程,2007,21(2):78-81. LU Gang, XING Yude, WU Junlin, et al. Fast scanning algorithm of the adjacent well anticollision calculations[J]. Petroleum Geology and Engineering, 2007,21(2):78-81. [17]董本京,高德利,柳贡慧.井眼轨迹不确定性分析方法的探讨[J].天然气工业,1999,19(4):59-63. DONG Benjing, GAO Deli, LIU Gonghui. Discussion of trajectory uncertainty analysis methods[J]. Natural Gas Industry, 1999,19(4):59-63. [18]刁斌斌,高德利.邻井定向分离系数计算方法[J].石油钻探技术,2012,40(1):22-27. DIAO Binbin, GAO Deli. Calculation method of adjacent well oriented separation factor[J]. Petroleum Drilling Techniques, 2012, 40(1): 22-27. [19]SAWARYN S J, JAMIESON A L, MCGREGOR A E. Explicit calculation of expansion factors for collision avoidance between two co-planar survey error ellipses[R]. SPE 159840, 2012. [20]赵舒展.遗传算法研究与应用[D].杭州:浙江工业大学,2006. ZHAO Shuzhan. Genetic algorithm research and application[D]. Hangzhou: Zhejiang University of Technology, 2006. [21]史玉才,管志川,朱宽亮. 大型丛式井组井口分配模型及其自适应遗传算法[J]. 中国石油大学学报(自然科学版),2012,36(6):70-73. SHI Yucai, GUAN Zhichuan, ZHU Kuanliang. Wellhead allocation model for large scale cluster well and its self-adaptive genetic algorithm[J]. Journal of China University of Petroleum(Edition of Natural Science), 2012,36(6):70-73. [22]唐世浩,朱启疆. 遗传算法中初始种群与交叉、变异率对解的影响及其解决方案[J]. 科技通报,2001,17(3):1-7. TANG Shihao, ZHU Qijiang. Effects of the initial population, crossover and mutation rate to the results of genetic algorithms and a possible solution scheme[J]. Bulletin of Science and Technology, 2001,17(3):1-7. [23]李大卫,王莉,王梦光. 变异算子及其最优变异率[J]. 系统工程与电子技术,1999,21(5):48-50,54. LI Dawei, WANG Li, WANG Mengguang. A new mutation operator and optimal mutation rate[J]. Systems Engineering and Electronics, 1999,21(5):48-50, 54. [24]周远晖,陆玉昌,石纯一. 基于克服过早收敛的自适应并行遗传算法[J]. 清华大学学报(自然科学版),1998,38(3):93-95. ZHOU Yuanhui, LU Yuchang, SHI Chunyi. Adaptive and parallel genetic algorithm based on solving premature convergence[J]. Journal of Tsinghua University (Sci & Tech), 1998,38(3):93-95. (编辑刘为清) Drilling sequence optimization model and its solution method for offshore cluster wells CAO Xiangfeng1,2, GUAN Zhichuan1, SHI Yucai1, XUE Lei1, ZHANG Xin3 (1.School of Petroleum Engineering in China University of Petroleum, Qingdao 266580, China;2.DrillingTechnologyResearchInstitute,ShengliPetroleumEngineeringCompanyLimited,Dongying257017,China;3.CNOOCSafetyTechnologyServiceCompanyLimited,Tianjin300452,China) Due to more wells and small wellhead space of offshore cluster wells, optimizing drilling consequence is helpful for anti-collision and batch drilling. Considering the anti-collision and the requirements of batch drilling, the wellbore separation factor was selected as the evaluation index of the wellbore collision risk assessment, and the minimum total length of anti-collision intervals of the whole cluster was selected as the optimal index of drilling consequence optimization to establish a mathematical drilling consequence optimization model and a genetic algorithm for offshore cluster wells. Also a living example was solved and discussed. The results show that it is feasible to select the minimum total length of anti-collision intervals as the optimal index to establish the drilling consequence optimization model. The drilling consequence optimization method can satisfy the requirements of anti-collision and batch drilling for offshore cluster wells. offshore cluster wells; drilling sequence; optimization model; anti-collision; batch drilling; genetic algorithm 2016-01-10 国家“863”计划(2012AA091501);中石化集团公司项目(13JP10006) 曹向峰(1979-),男,高级工程师,博士研究生,研究方向为钻井工程。E-mail:chaoxiangfeng.slyt@sinopec.com。 1673-5005(2016)03-0096-06doi:10.3969/j.issn.1673-5005.2016.03.012 TE 21 A

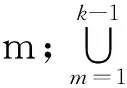
2 遗传算法求解方法
3 实例分析

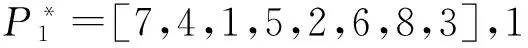



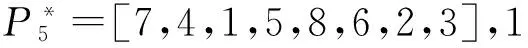
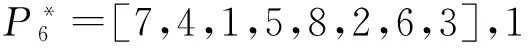
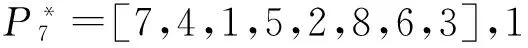

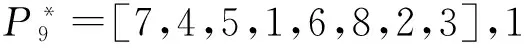

4 结束语
