三电平DPWM光伏逆变器的中点平衡控制

龚仁喜，钟榕蓉，刘　畅，彭立亮

(广西大学 电气工程学院， 南宁　530004)



三电平DPWM光伏逆变器的中点平衡控制

龚仁喜，钟榕蓉，刘畅，彭立亮

(广西大学 电气工程学院， 南宁530004)

传统中点平衡控制方法运用在三电平DPWM(discontinuous pulse-width modulation)逆变器中会打乱DPWM的箝位区域，从而使DPWM策略失效。针对该问题提出了一种新的中点平衡控制方法。此方法在中点电位波动大于正限值时将距离负电平最近的一相箝位于负电平，在小于负限值时将距离正电平最近的一相箝位于正电平，由此推算出调中点电位时刻应注入调制波的零序电压分量。搭建Simulink模型及由DSP控制器和Q8构成的半实物仿真实验平台，对所提算法分别进行了离线仿真及硬件在环(hardware-in-the-loop,HIL)仿真实验，证明了所提算法的可行性及有效性。此方法能简单有效地控制中点电位平衡，无需在每个载波周期都进行复杂的计算即可达到控制目的，同时能确保DPWM低开关损耗的特性。

中点平衡控制；不连续脉宽调制；三电平逆变器；硬件在环仿真

二极管箝位式电路拓扑(NPC)是运用最为广泛的多电平并网逆变器拓扑。相比传统两电平逆变器，NPC逆变器具备du/dt、总谐波畸变率(THD)小、器件电压应力低的优点，所以更适用于中高压大功率电能变换和交流驱动场合[1-2]。随着光伏电站功率的不断攀升[3]，NPC逆变器将逐渐成为大中型并网光伏逆变器的主流结构。

在电力变换系统中，器件损耗(包括导通损耗和开关损耗)是影响系统效率至关重要的一环，而变换器的开关损耗与具体的调制方式有很大关系，改进调制方式可以在一定程度上减小开关损耗。为此，有学者提出了不连续脉宽调制(discontinuous pulse width modulation，DPWM),将每个开关周期的开关次数降低到连续调制(continuous pulse width modulation， CPWM)时的2/3，大大地降低了开关损耗。相较于CPWM，在开关频率相同情况下，DPWM可使开关损耗降低1/3[4]。在中高压功率变换要求开关频率较低的场合，若保证与CPWM相同的开关损耗，DPWM可将开关频率提高50%，因而可降低滤波器设计难度和成本，减小体积，同时提升系统动态性能。近年来，越来越多的研究将DPWM运用到三电平的功率变换器中[5-10]。

虽然将三电平DPWM运用到NPC光伏逆变器中既能提高系统效率又可改善系统性能，但其固有的中点电位不平衡问题仍然存在，若不加以控制，会对输出电压及电流产生较严重的负面影响[11]。目前， 基于CPWM的NPC逆变器中点平衡方法主要有2种：载波CPWM逆变器采用向原始调制波注入零序分量的方法[12-13]；空间矢量CPWM逆变器多使用调节平衡因子的方法[14-16]。两种方法的本质相同，即都是通过调节每个开关周期内冗余正负小矢量的作用时间以达到中点平衡控制的目的。近年，也陆续有新方法被提出，例如：文献[16]提出了变虚拟空间矢量方法，通过正负小矢量作用时间及虚拟中矢量产生的电流控制中点电位；文献[17]提出了模型预测控制方法，通过优化预测电流与参考电流之间的平方差及中点电位的偏差值构成的性能指标函数来控制中点电位，具备较快的动态响应速度。

然而，上述方法都是在CPWM基础上提出的，若将方法移植到DPWM中，由于DPWM的箝位特性，并不能取得好的效果，甚至会打乱其箝位特性，从而导致DPWM失去其开关损耗低的优势。针对DPWM变换器的中点电位平衡控制，文献[3]指出：某些扇区内相电流很小，因而开关损耗很小，可采用传统调节正负小矢量作用时间的方法调节中点电位，而余下扇区则可采用DPWM策略且不对中点电位进行控制，但并未提及基于DPWM特性的有效中点平衡控制方案。文献[7]提出：在每个开关周期交替注入两路对中点电位影响相反的零序电压的办法，但该方法本质上仍采用两电平的DPWM策略，且在调节中点电位期间增加了开关动作，并不能很好地发挥DPWM低损耗的特性。总体而言，迄今为止基于DPWM的中点电位平衡控制方法鲜有研究成果呈现。

1　三电平NPC逆变器的不连续脉宽调制

1.1三电平DPWM

本文将三电平NPC光伏逆变器作为研究对象，电路拓扑如图1所示。在光伏逆变器中，通常要求运行在单位功率因数，因此本文的分析基于功率角为0，且假设输出滤波电感足够小，以使逆变器的并网电压电流同相。三电平逆变器每相输出Udc/2，0，-Udc/2这3种电平，分别用1，0，-1共3个状态表示，三相的开关状态组合构成了27个空间矢量，如图2所示。

图1　三电平NPC光伏逆变器主电路拓扑

图2　三电平空间矢量

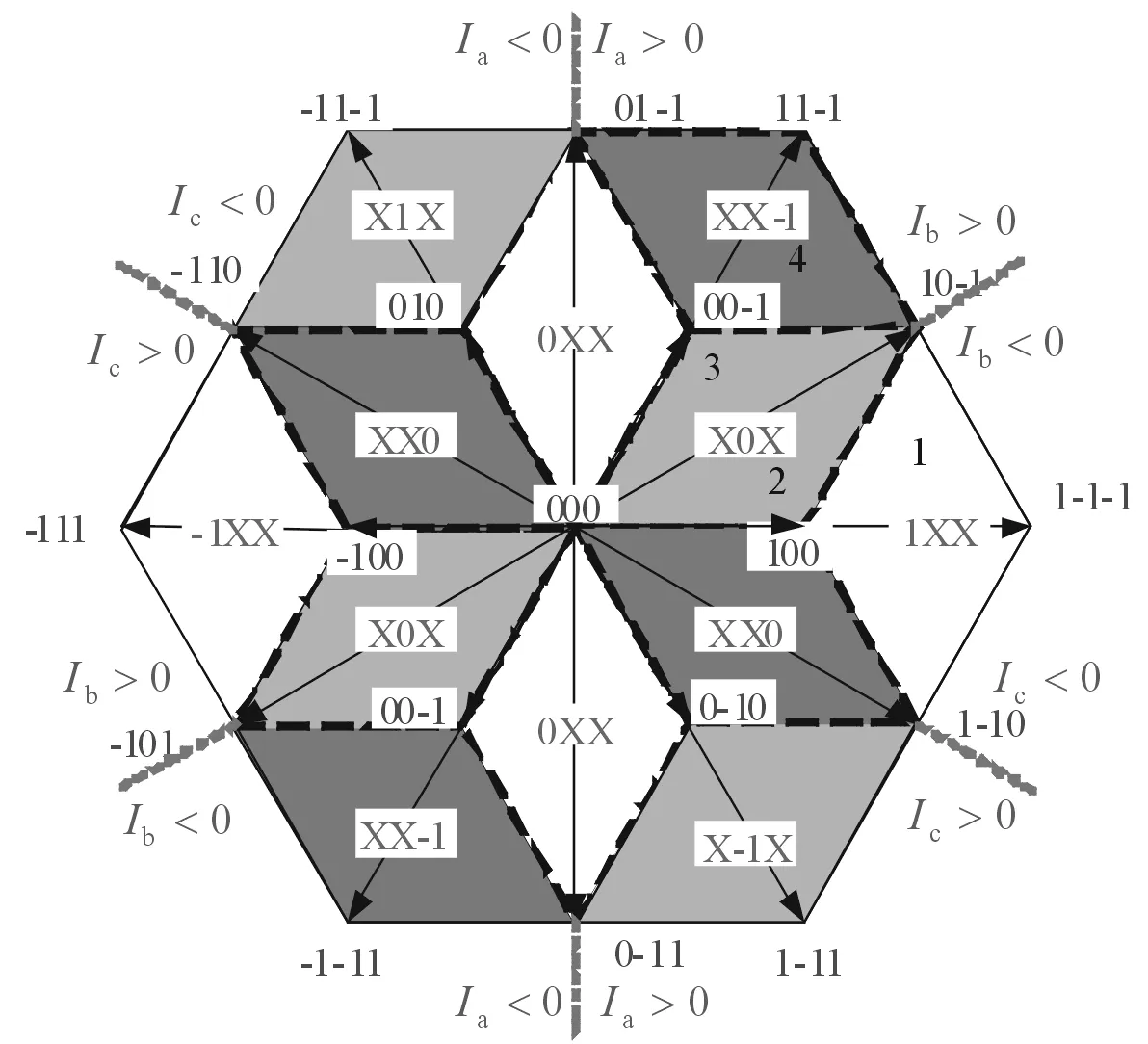
图3　DPWMA箝位区域(1XX表示A相箝位于正电平)

A相原始调制波添加Vz后波形如图4所示。任意相在每个基波周期内都存在箝1，0，-1的区域，每一时刻只有其中一相箝位，随着调制度M的变化，1，0，-1所占比例也会发生变化。

图4　DPWMA的调制波(M=0.9)

1.2DPWM下的中点电位不平衡问题分析

Udc2,Udc1,vo,io分别为直流侧上下电容电压、中点电位及中点电流，并定义流出O点的电流方向为正方向，如图1所示，且

(2)

分析图5和表1可知：零矢量、大矢量不产生流过中点O的电流，不影响中点电位vo；正小矢量产生流入O点的电流，导致vo升高；负小矢量产生流出O点的电流，导致vo降低；中矢量产生的电流等于某相电流，此电流既可能流入也可能流出O点，所以vo既可能升高也可能降低，视合成参考矢量所处扇区而定。

与CPWM不同，DPWMA在每个载波周期内仅采用冗余小矢量对中的1个(表1带下标的小矢量为DPWMA策略下摒弃的小矢量)。

图5　不同开关状态对中点电位的影响

矢量幅值开关状态中点电流io0矢量0[000][111][-1-1-1]0小矢量Udc3正负正负[100][0-1-1]-iaia[110][00-1]ic-ic[010][-10-1]-ibib[011][-100]ia-ia[001][-1-10]-icic[101][0-10]ib-ib中矢量3Udc3[10-1][-101]ib[01-1][0-11]ia[-110][1-10]ic大矢量2Udc3[1-1-1][11-1][-11-1][-111][-1-11][1-11]0

接下来分析DPWMA策略下的vo波动情况。以图3的第I扇区为例，将其划分为4个小扇区。在1、2扇区(0°～30°)，正小矢量[100]和中矢量[10-1]作用产生的中点电流io分别为-ia和ib(ia>0，ib<0)，则每个载波周期内io平均效果为负，即电流流入中点O，从而使vo升高；在3、4扇区(30°～60°)，负小矢量[00-1]和中矢量[10-1]作用产生的io分别为-ic和ib(ic<0，ib>0)，则扇区内的每个载波周期内io平均效果为正，即电流流出中点O，从而使vo降低。

合成参考矢量进入第II扇区后，情况类似。当参考矢量旋转1个基波周期后，vo形成了频率3倍于基频的振荡，如图6所示。当6个大扇区的平均电流绝对值不相等时，会产生vo偏移。随着时间的推移偏移量变大。长时间的持续偏移将导致直流侧上下电容的严重不均压，如图7所示。

中点平衡的控制目标即消除图7的直流偏移，并尽量减小图6的3倍频波动幅值。

2　DPWM下的中点电位平衡控制

2.1传统中点平衡控制方法在DPWM中的局限

在CPWM逆变器中，通过注入零序分量Vz的方法调节中点电位。注入Vz后会改变正负小矢量的作用时间，如图8所示。若中点电位vo过大，则可向调制波中注入负的零序电压Vz。注入Vz后，正小矢量[110]作用时间减小，负小矢量[00-1]的作用时间增大，可达到降低vo的控制目的。

图6　vo的3倍基频振荡

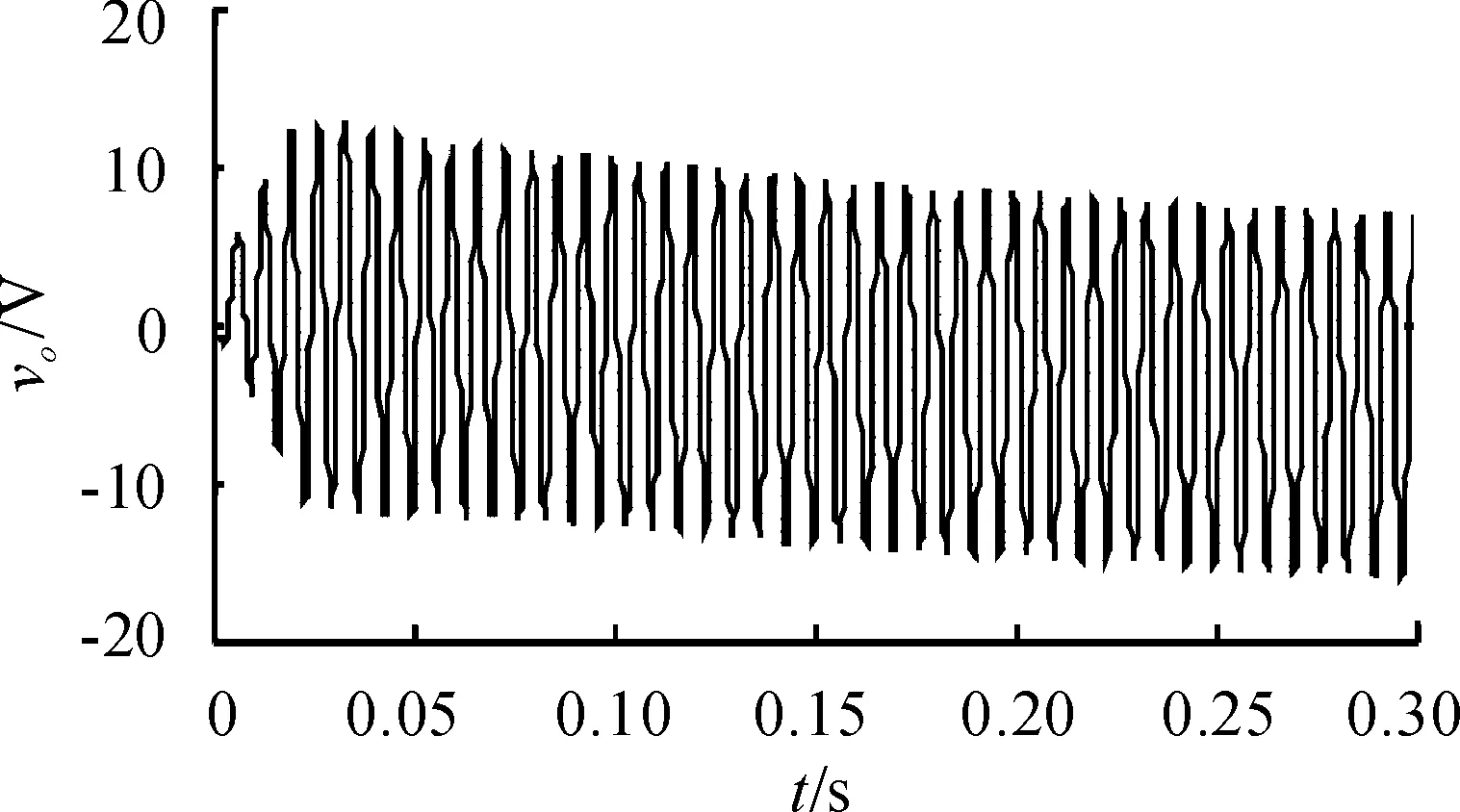
图7　vo的直流偏移

若将传统中点平衡方法移植到DPWM中，假设某一时刻B相箝位在0电平时(图3中第I大扇区的第2小扇区)，vo超出正限值，此时需要注入负的Vz以降低vo。注入Vz后，开关序列将从DPWM的5段式退化为CPWM的7段式，失去了DPWM的低损耗特性。

由于DPWM中每个载波周期只使用一对冗余小矢量当中的1个，而无法像传统CPWM那样通过调节1个载波周期内的正负小矢量作用时间来达到调节中点平衡的目的，因此传统的中点平衡控制方法不适用于DPWM逆变器。

2.2基于DPWM的中点电位平衡策略

通过上文分析可知：正小矢量令vo增大，负小矢量令vo降低。为此，本文提出一种可称为箝位法的中点电位调节方法：若vo大于正限值，将某相箝位于-1电平使负小矢量作用时间增加，从而降低vo；若vo小于负限值，将某相箝位于+1电平使正小矢量作用时间增加，从而提高vo。原理如图9所示，vo会在合成参考矢量从第I大扇区的小扇区2过渡到小扇区3时达到正向峰值。若期间vo大于系统允许的最大中点电位值时，可将C相(从图9可知，此时C相是距离-1电平最近的相)箝位在-1电平，开关序列由[10-1] [100] [000] [100] [10-1]变为[1-1-1] [10-1] [00-1] [10-1] [1-1-1])，负小矢量[00-1]的占空比较大，可以有效地在短时间内降低vo且不增加开关动作次数，确保了DPWM的低损耗特性。相反，当某个时刻vo的值小于系统允许的最小中点电位值时，可将三相中距离+1电平最近的一相箝位在+1电平，以增加正小矢量的作用时间。

图8　传统中点电位平衡策略原理

上述中点电位平衡方法是在空间矢量的基础上进行的分析，为通过载波实现所提算法，将各扇区的中点平衡控制作对比发现，仅需向三相调制波中注入式(3)的零序分量：

(3)

Δ为根据直流母线电压及其他逆变器性能指标所设定的中点电位阈值。

算法的流程如图10所示。

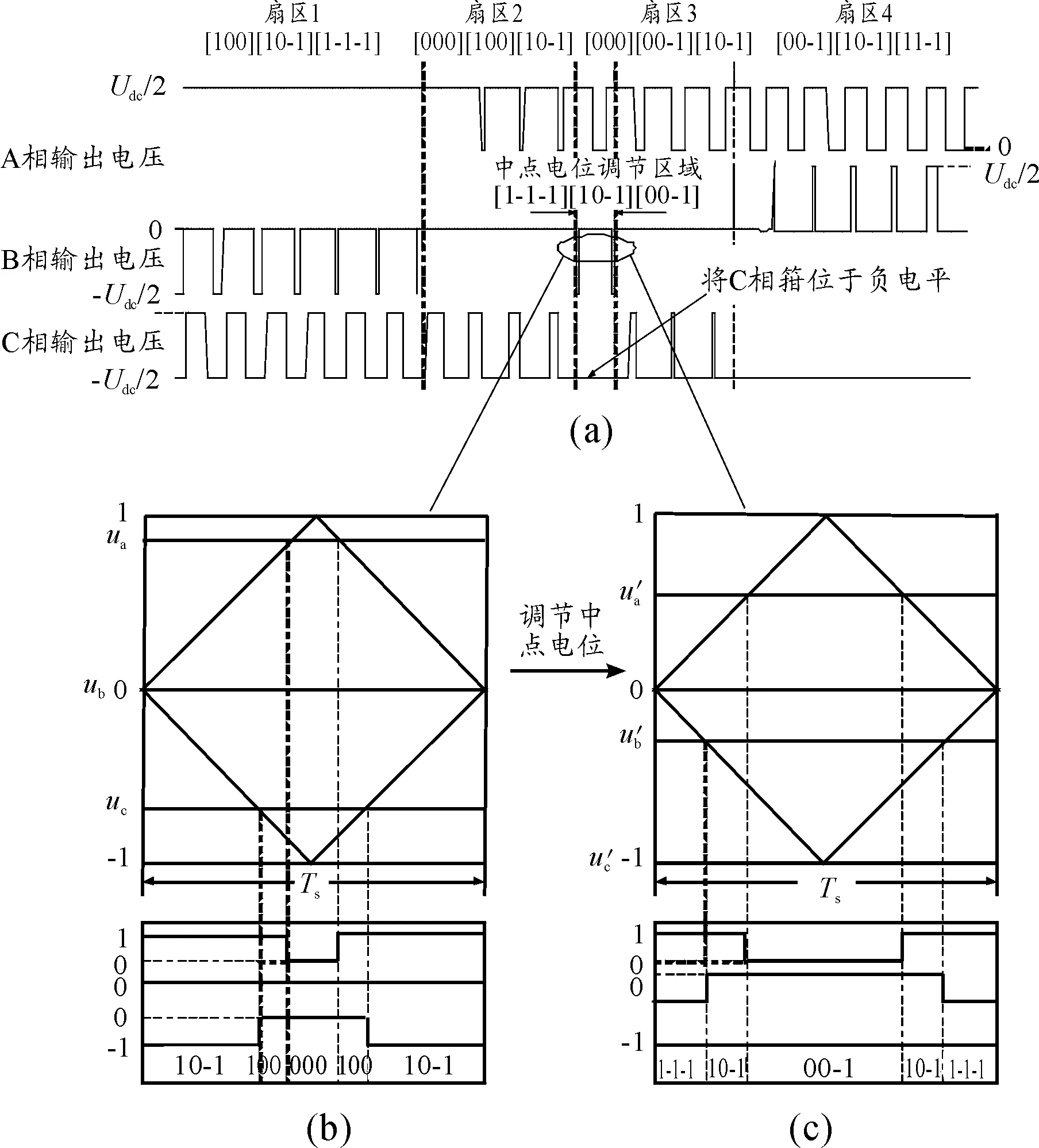
图9　箝位法调节中点电位原理

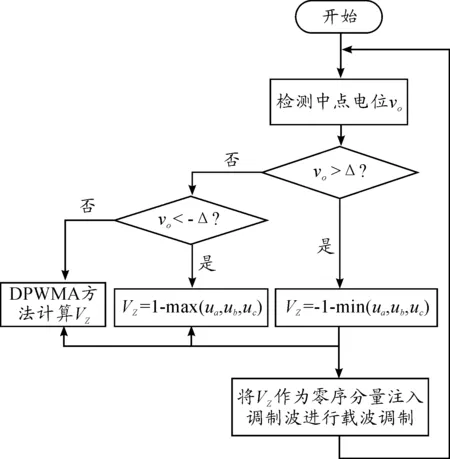
图10　箝位法调节中点电位流程

算法步骤：

1) 按式(2)检测中点电位vo；

2) 若vo<-Δ或vo>Δ，按式(3)计算Vz；

3) 若-Δ≤vo≤Δ，按DPWMA规则计算Vz；

3　离线及硬件在环仿真验证

3.1离线仿真

为了验证所提方法的准确性及有效性，搭建单级式三电平NPC光伏逆变系统的Simulink仿真模型，及由Q8和DSP控制器构成的硬件在环仿真实验平台分别进行离线仿真及硬件在环仿真验证，所涉及的主要参数见表2。

表2　相关参数

图11是未进行中点电位平衡调节的相关波形。可见上下电容电压起始时刻存在40 V电压差(即vo=-40 V)，且经过长时间后此电压差并未消除。

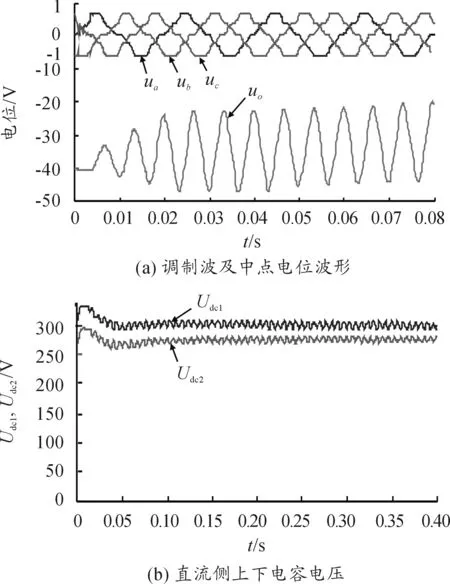
图11　未调节中点电位

图12是将论文[8]所提的传统中点平衡方法用到DPWMA中的仿真结果。与图4相比，调制波的箝位特性遭到破坏，增加了大量的开关动作。此外，逆变器的共模电压增大、输出谐波含量增加，系统的控制性能下降。由此验证了传统中点平衡控制方法不适用于DPWM逆变器的结论。

图12　采用传统中点平衡控制方法

图13是采用所提中点电位平衡策略后的相关波形，设置阈值Δ=12 V。对比图11，图13(a)的三相调制波起始的几个周期中存在短暂的调节中点电位区域，0.07 s后，vo稳定；图13(b)中的上下电容电压不再有直流偏差。

图13　采用所提中点平衡控制方法

3.2硬件在环仿真

为了进一步验证算法的实用性，本文搭建了Q8+DSP的硬件在环实验平台。Q8全称为Quanser8 Hardware in the Loop Board，通过识别光伏逆变系统的主电路Simulink模型作为虚拟的被控对象。DSP作为控制器采集Q8输出的相关电压电流信号进行计算，并向Q8输出12路DPWM波信号控制功率管的通断。DSP控制器的型号为TMS320F28335。HIL仿真实验平台的系统框图如图14所示。

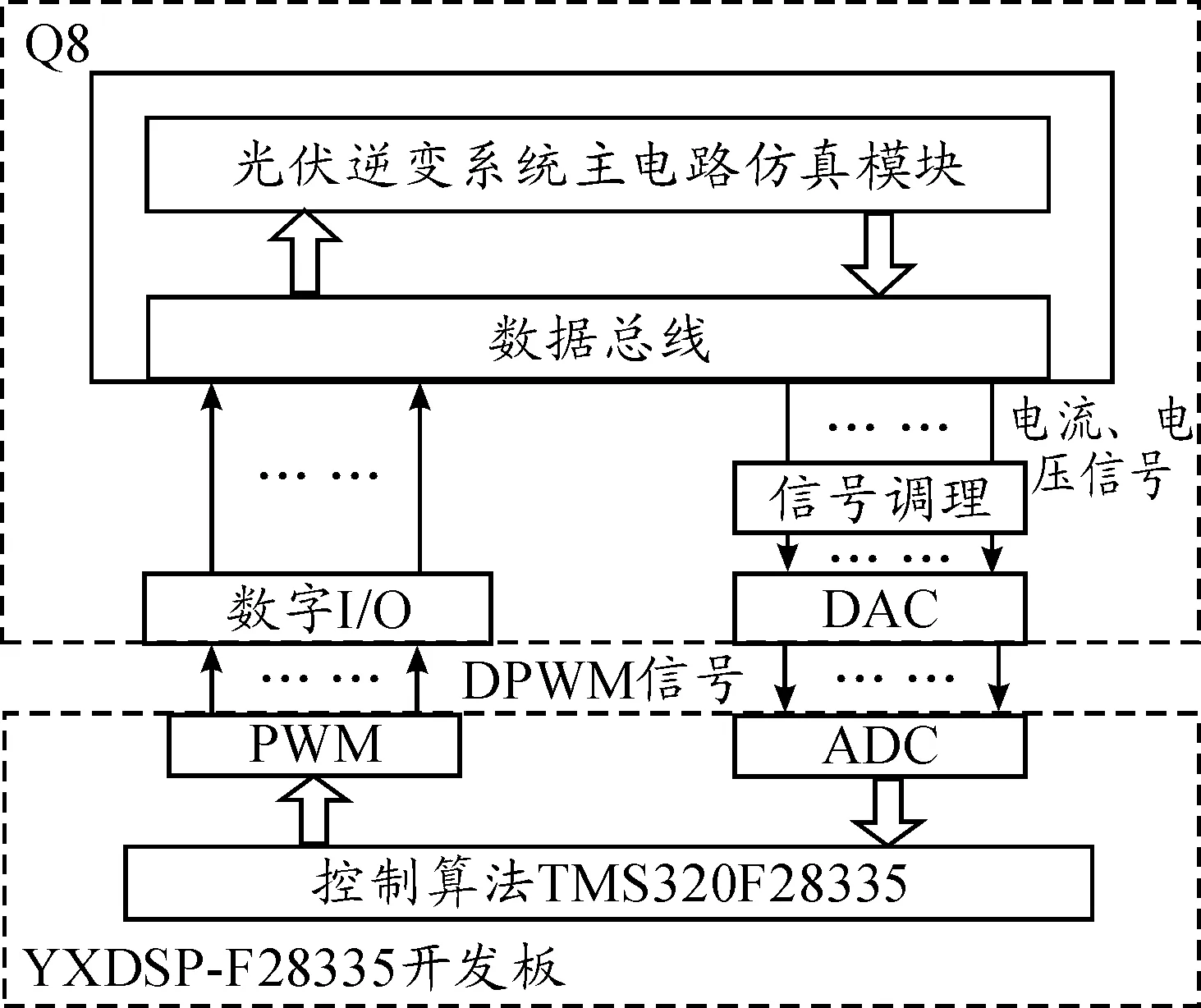
图14　Q8+DSP硬件在环仿真系统框图

用示波器观测到的实验波形如图15所示。

图15　中点电位vo的调节效果

由图15可知：在调节中点电位前，vo不稳定，存在与图7仿真结果相似的直流偏移及较大的峰峰值(最大达32 V)；调节中点电位后(设置阈值Δ=8 V)，vo的直流偏移得以消除，峰峰值为16 V左右。

4　结束语

本文所提方法能简单有效地调节中点电位平衡，不影响DPWM的低开关损耗优势。理论上可将阈值设置得尽量小，以减小vo的低频(3次)波动幅值，但如此会造成中点电位调节时间在一个基波周期内的比重过大，从而增加共模电压。因此，采用DPWM无法做到完全消除中点电位的低频波动。但在工程运用中，只需消除vo的直流偏移，同时将低频波动的幅值限制在直流母线电压的5%以内即可满足工程需求。本文所提方法能满足此要求。

[1]YARAMASU V,WU B.Predictive Control of Three-Level Boost Converter and NPC Inverter for High Power PMSG-Based Medium Voltage Wind Energy Conversion Systems[J].IEEE Transactions on Power Electronics,2014,29(10):1-1.

[2]ABU-RUB H,HOLTZ J,RODRIGUEZ J,et al.Medium-Voltage Multilevel Converters—State of the Art,Challenges,and Requirements in Industrial Applications[J].Industrial Electronics IEEE Transactions on,2010,57(8):2581-2596.

[3]梁秀璟.台达:持续关注中国光伏逆变器市场[J].自动化博览,2016(1):85-87.

[4]KAKU B,MIYASHITA I,SONE S.Switching loss minimised space vector PWM method for IGBT three-level inverter[J].IEE Proceedings-Electric Power Applications,1997,144(3):182-190.[5]ZHANG X,WANG Q,BURGOS R,et al.Discontinuous pulse width modulation methods with neutral point voltage balancing for three phase Vienna rectifiers[C]//Energy Conversion Congress and Exposition.[S.l.]:IEEE,2015.[6]BEIG A R,KANUKOLLU S,AL HOSANI K,et al.Space-Vector-Based Synchronized Three-Level Discontinuous PWM for Medium-Voltage High-Power VSI[J].IEEE Transactions on Industrial Electronics,2014,61(8):3891-3901.

[7]LAUTTAMUS P,TUUSA H.Design of discontinuous switching sequences in the case of grid-connected three-level voltage-source converter[C]// Power Electronics Conference.[S.l.]:IEEE,2010:760-767.

[8]张帅,牛宏侠,侯涛.三电平逆变器SVPWM参考矢量区域快速判断研究[J].电机与控制应用,2015(7):29-33.

[9]DALESSANDRO L,ROUND S D,DROFENik U,et al.Discontinuous Space-Vector Modulation for Three-Level PWM Rectifiers[J].IEEE Transactions on Power Electronics,2008,23(2):530-542.

[10]冯九一,宋文祥,姜书豪,等.三电平有源钳位逆变器同步优化PWM方法[J].电机与控制应用,2015,42(11):10-15.

[11]YOO S,LEE J S,LEE K B.A new discontinuous PWM method of three-level inverter for neutral-point voltage ripple reduction[C]// International Conference on Power Electronics and Ecce Asia.[S.l.]:IEEE,2015.

[12]宋强,刘文华,严干贵,等.基于零序电压注入的三电平NPC逆变器中点电位平衡控制方法[J].中国电机工程学报,2004(5):61-66.

[13]姜卫东,杨柏旺,黄静,等.不同零序电压注入的NPC三电平逆变器中点电位平衡算法的比较[J].中国电机工程学报,2013(33):17-25.

[14]宋文祥,陈国呈,武慧,等.一种具有中点电位平衡功能的三电平空间矢量调制方法及其实现[J].中国电机工程学报,2006(12):95-100.

[15]张长信.NPC三电平变流器中点平衡算法的研究[D].合肥：合肥工业大学,2012.

[16]桂石翁,吴芳,万山明,等.变虚拟空间矢量的三电平NPC变换器中点电位平衡控制策略[J].中国电机工程学报,2015(19):5013-5021.

[17]王美龄,王丽梅,孙永亮.一种基于模型预测控制的T型三电平逆变器中点电位平衡控制方法[J].电气工程学报,2015(9):66-72.

(责任编辑杨黎丽)

Neutral-Point Potential Balancing Control of Three-Level Discontinuous PWM PV-Inverters

GONG Ren-xi, ZHONG Rong-rong, LIU Chang, PENG Li-liang

(College of Electrical Engineering, Guangxi University, Nanning 530004, China)

To solve the problem that the DPWM’s advantage of low switching losses will be destroyed when traditional neutral-point potential balancing methods are applied in DPWM inverters, a new balancing method was developed. The proposed method was implemented by clamping one phase-leg to negative DC-bus when the potential is higher than the positive limit, or positive DC-bus when the potential is lower than the negative limit, according to which the zero-sequence voltage was calculated to balance the neutral-point potential. Then, a Simulink model and a hardware-in-the-loop (HIL) testing platfrom composed of a Q8 model and a DSP controller were built, whose simulation and experiment results were verified the validity and feasibility of the proposed method. This method maintains low switching losses of DPWM and balances the neutral-point potential effectively and more simply, without extra complex calculations in every period of carrier-wave like the traditional method.

neutral-point potential balancing; DPWM; three-level inverters; HIL simulation

2016-03-28

国家自然科学基金资助项目(61561007)

龚仁喜(1962—)，男，广西桂林人，教授，博士生导师，主要从事电力电子技术及应用、智能检测技术研究，E-mail:rxgong@gxu.edu.cn；钟榕蓉(1987—)，女，广西南宁人，硕士研究生，主要从事新能源电力变换研究。

format：GONG Ren-xi, ZHONG Rong-rong, LIU Chang, et al.Neutral-Point Potential Balancing Control of Three-Level Discontinuous PWM PV-Inverters[J].Journal of Chongqing University of Technology(Natural Science)，2016(9):87-94.

10.3969/j.issn.1674-8425(z).2016.09.014

TP23

A

1674-8425(2016)09-0087-08

引用格式：龚仁喜，钟榕蓉，刘畅，等.三电平DPWM光伏逆变器的中点平衡控制[J].重庆理工大学学报(自然科学)，2016(9):87-94.