课堂教学的专家评价与学生评价一致性分析

李国辉，耿　辉，冯　静，杨文尧

(国防科学技术大学　1.信息系统与管理学院；2.训练部，湖南　长沙　410073)



课堂教学的专家评价与学生评价一致性分析

李国辉1，耿辉2，冯静1，杨文尧1

(国防科学技术大学1.信息系统与管理学院；2.训练部，湖南长沙410073)

结合专家评价和学生评价的综合评价是课堂教学评价中的一种重要方法。这里的问题是专家评价和学生评价是否一致呢？本文以某高校抽取的评优教师的专家和学生评分作为样本，采用描述性统计法、图形分析法和Kappa统计量法，分析二者的一致性程度。

课堂教学评价；学生评教；专家评教；一致性分析

在人才培养的质量工程中，课堂教学的评价工作是一个重要环节。教学评价是教学质量监控体系中的核心。

早在上世纪20年代的美国，一些高校中就开展了评教工作。到上世纪80年代，学生评教在一些国家兴起，成为高校教学评估中日常管理的一部分[1]。随着评价标准的不断规范和完善，美国许多州的高校建立起了一套以提高教师的自我参与、自我督促和自我完善能力为目的的评估体系。

上世纪80年代中期，我国开始开展课堂教学的评价工作。此时学生评教也才逐步开展。经过30多年的时间，我国高校的教学评价体系已基本建立起来[2]。其中专家评价与学生评价相结合的方法是目前一种重要的评价方法[3]。有学者[4]给出了基于非参数方法对课堂教学的评价一致性问题进行建模，而本文将主要利用实际的评价数据进行统计分析，研究专家评价与学生评价相结合的课堂教学评价问题。专家评价是以教学经验丰富的教授作为主体组成教学督导组，通过随机听课的方式来进行评教，而学生评价是全体学生们通过网上的教学评价系统来对授课教师进行评价。最后综合专家评价与学生评价的得分作为教师课堂教学的最后评价。

对于课堂评价中的专家评价与学生评价，哪个更客观一些呢？学生是学习的主体，全程接受教师的授课，他们对教师的评价应该更全面。但是专家评教是一种专业评教，在评价教师的课堂教学形式、教学内容设计和讲授内容组织和表述准确性方面，评价更为客观。而学生评教可能会带有任务性和随意性。本文不讨论专家评价与学生评价哪个更为合理，而是用采集的评价数据来分析两者的一致性问题，用数据来说话。本文通过描述性统计法、图形分析法和Kappa统计量法对专家评价与学生评价的一致性程度进行分析，给出一些建议从而进一步促进课堂教学评价工作的改进。

一、一致性检验的描述性统计

描述性统计分析是指对收集到的数据进行位置特征、离散特征、形态特征及图形的分析，确定数据的统计分布情况。

1.偏倚程度和扁平程度。数据的偏倚度分为如下三种情况：如果数据的频数分布曲线以平均数为中心，左右两边形状对称，那么称为对称分布；如果频数分布曲线的峰部偏向左边，尾部拖向右边，称为右偏分布或正偏分布；如果频数分布曲线的峰部偏向右边，尾部拖向左边，称为左偏分布或负偏分布。在数据的扁平程度度量方面，如果分布曲线的峰态值为3时，曲线呈正态分布曲线；如果分布曲线的峰态值大于3时，曲线呈尖顶曲线；如果分布曲线的峰态值小于3时，曲线呈平顶曲线。

2.集中趋势和离散趋势。集中趋势由数据的位置特征所反映，离散趋势由数据的离散特征所反映。数据的离散程度越大，位置特征对数据的代表性也越差；数据的离散程度越小，位置特征对数据的代表性也就越好。集中趋势的度量参数包含平均值、中位数和众数。离散趋势的度量参数包含极差、四分位值、方差或标准差。

3.相关关系与散点图。两个变量之间的相关关系可以通过散点图来直观地表示出来。它将两个变量形成的成对数据用点的形式标在平面直角坐标系上。对这些点形成的散布进行分析，就可以看出变量xi和yi(i=1,2,…,n)之间的相关关系，用r表示。

(1)

根据实际数据计算出的r，其取值一般分布在-1与+1之间。那么r的绝对值越接近1，表示两个变量之间的相关程度越高；r的绝对值越小，两者的相关程度越低。

散点图是用来描述两种变量之间相关性的直观图。在直角坐标系中，自变量为横坐标，因变量为纵坐标。坐标系中的每一个点代表一组数据。多组数据由多个点表示，此时这些点是根据两种变量之间的相关关系散布在坐标系中。我们可以根据散点图的分布情况来直观地判断出两个变量之间的相关性强度。

二、数据一致性的Kappa统计量法

Kappa统计量是用来比较两个或多个观测者对同一事物，或者同一观测者对同一事物的两次或多次观测结果是否一致的统计指标量，用于度量判别类结果的一致性。以两个观察者为例，如图1所示。设Po为两个观察者判断一致的概率，有：

(2)

其中，N为总的样例数；TP为真正例，TN为真反例，是两者观察一致的样本数量；FP为伪正例，FN是伪反例，是两者观察不一致的样本数量。P1和P2分别是观察者1和观察者2判断为真的样本总数，N1和N2分别是观察者1和观察者2判断为假的样本总数。P1+N1 =P2+N2 =N.

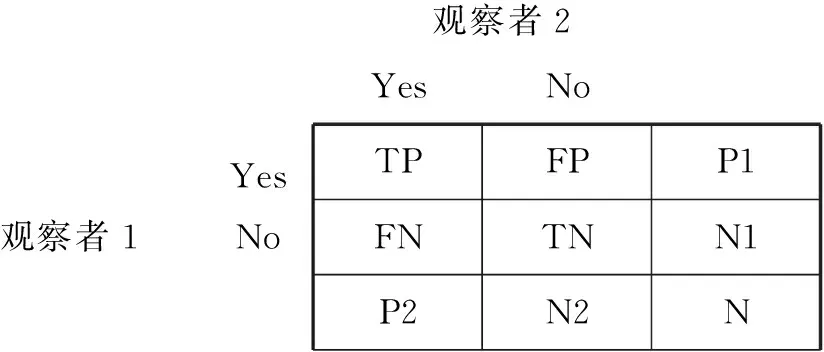
观察者2YesNo观察者1 Yes No TPFPP1FNTNN1P2N2N

图1Kappa统计量计算

设Pe为随机情况下的期望一致率，即两个观察者判别的结果因为偶然机会所造成的一致率。采用边缘统计量来计算：

(2)

Kappa统计量的定义为：

(3)

Kappa系数是两个差值的比值，其中分子为实际观察到的一致率和可能的期望一致率之差。分母表示非随机情况下的一致率。

Kappa系数取值范围一般在-1到1之间。如果Kappa系数为1，表明两个观察者的判断结果完全一致；如果Kappa系数为0，表明两个观察者的结果完全是因为随机造成的，完全不一致；当不一致比一致更多，Kappa系数为负值。易知Kappa系数越大，一致性程度越好。通常情况下，如果kappa系数位于0.21-0.40范围的一致性是“可接受的”，位于0.41-0.60范围的一致性是“中等的”，位于0.61-0.8范围的一致性是“较大的”，大于0.81的一致性是“非常好的”。

三、专家与学生评教数据的描述性统计分析

我们尝试对一个学期中参与课堂教学评优的评价数据进行分析。选取某个学期总共参与评优的教师共有97人。然后将这97名教师的专家评价的结果与学生评价的结果进行比较。在时间一致，对象样本一致，数据具有可比性的前提下，分析专家评价和学生评价结果的一致性。表1是专家打分与学生打分的各个描述性统计量。需要说明的是，我们对两组评分数据进行了归一化预处理，使得两组评价数据的均值趋于相等，以便进行归一化合并处理。

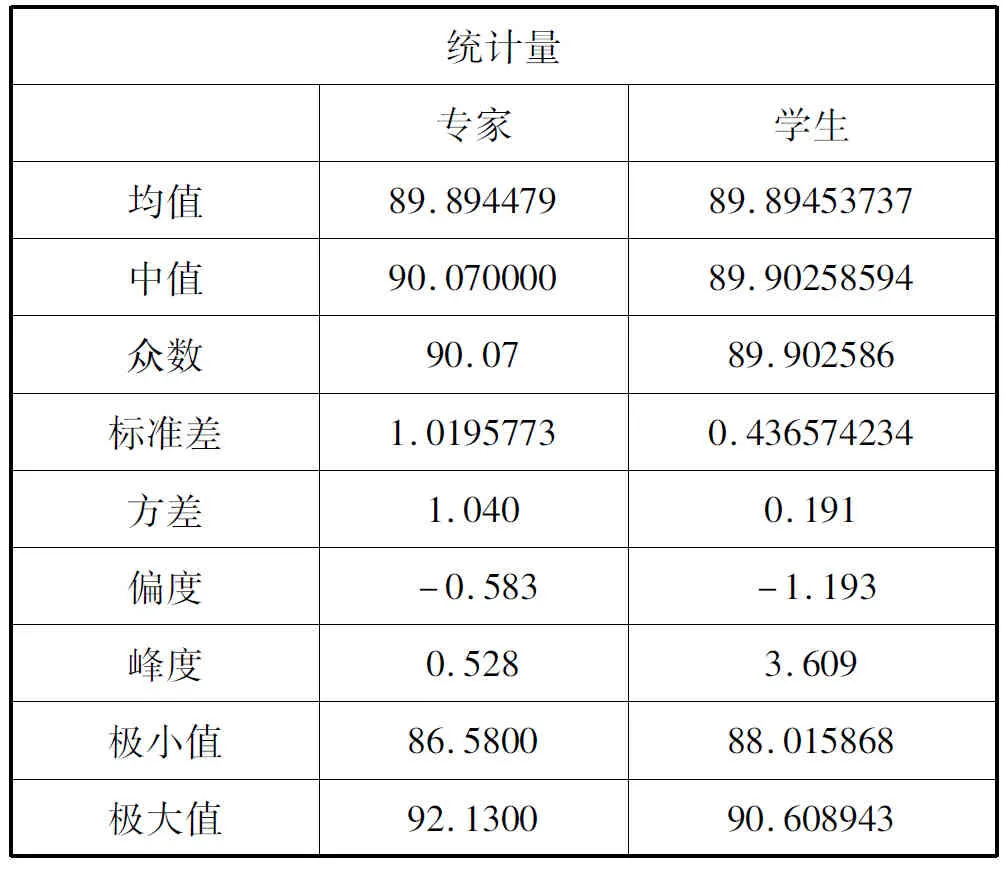
表1　专家打分和学生打分描述性统计结果

1.偏度分析。专家评价的偏度为-0.583，属于负偏；学生评价的偏度为-1.193，也属于负偏，都在“0>偏度>-3”的范围内，表示评分集中在高数值段内。但是学生偏度更大，表示学生更偏向给教师打高分。

2.峰态分析。专家打分的峰态为0.528，位于“峰态<3”的区间内，说明专家所给分数比较均匀地分散在众数的两侧。学生打分的峰态值为3.609，位于“峰态值>3”的区间内，说明学生所给分数较为密集的分布在众数的周围，区分度相对较小。

3.集中趋势与离散趋势分析。把专家评价和学生评价的平均值归一化到一致值，为89.89。这样的情况下，专家评价的标准差为1.020，学生评价的标准差为0.437。专家打分的标准差要比学生打分的标准差大0.583，这正好与专家打分的分数较为分散、均匀而学生打分较为集中的结论保持一致。专家认为这些教师之间存在一定的差距，所以所给的分数也有一定的差距，有一定的区分度，导致标准差较大；而学生所给的分数差别不大，相对集中一些，标准差只有0.437。

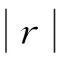
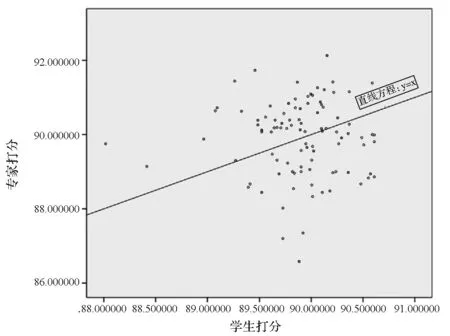
图2　专家打分与学生打分散点图

5.散点图分析。图2中每一个点代表一位教师的专家打分和学生打分的情况，横坐标为学生打分，纵坐标为专家打分。当某位教师的专家打分与学生打分相同时，相应的点便在拟合线y=x上。所以这条拟合线代表了专家打分与学生打分的一致性程度。

从散点图中可以看出，在拟合线上或周围的点分布较少，说明专家打分与学生打分相关关系较弱，图上的散点随机地分布在各处，几乎看不出二者之间的线性关系，所以专家打分与学生打分的一致性程度很低。直线上部的点表示学生打分较低而专家打分较高的教师，直线下部的点表示学生打分较高而专家打分较低的教师。这两种情况的数据分布基本相等。

四、专家与学生评教数据的图形分析法

教师的课堂教学总评分由专家打分和学生打分的加权平均值构成。我们用图形分析法分析总评分与专家打分和学生打分之间的一致性，得出一致性关系。首先，分析课堂教学的总评分与专家打分的一致性程度。将教师总分排名与专家打分排名进行对比，找出二者不同排名段内相同的教师的个数，用图3的形式表示。其中横坐标表示排名百分比，例如0.4表示排名前40%的被评价对象(教师)。纵坐标值(重合率)对应于该排名百分比下，总分进入前40%的被评价对象与专家打分进入前40%的被评价对象的相同对象比例。

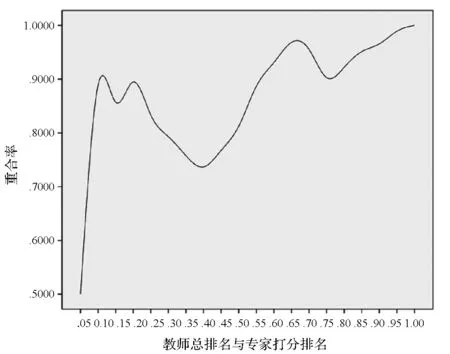
图3　教师总排名与专家打分的教师排名

专家打分排名和教师的总得分排名的重合率是很高的，基本上都是保持在80%以上的重合率，除了排名在前5%和30%到45%这段区间之外。在排名前5%的教师中，二者此时的重合率为50%。在教师排名的前40%这个点上，教师总排名与专家打分的教师排名的重合率达到了一个极小值点，此时重合率为73.68%，即排名前38名中，有28名是相同的。在教师排名的前65%这个点上，教师总排名与专家打分的教师排名的重合率达到了一个极大值点，此时重合率到达了96.83%，也就是说排名前63名中，有61名是相同的。所以总的来说，专家打分与总评分的一致性还是很高的，即二者的吻合度很高。说明专家打分时比较严谨认真，细心周全，所给分数比较客观合理，不会出现主观性很大的分数。

另外，再分析教师的总评分与学生打分的一致性程度，如图4所示。其横坐标和纵坐标的含义同图3。

从图4中看出，学生打分的教师排名与教师的总排名一致性程度较低，不是很理想。在教师排名的前4名和前9名里面，都是仅有一名教师是相同的，重合率仅为25%和11.11%；在排名的前14名和前19名里面，相同的也分别只有2名教师和3名教师，重合率仅为14.29%和15.79%。再从整个得到的数据来看，当学生打分的总排名超过75%之后，二者的重合率才超过80%。整体而言，相比于专家打分的排名来说，学生打分的排名与总排名的一致性程度就要差很多，尤其是排名越靠前的教师，学生打分的排名与总排名的差别越大。

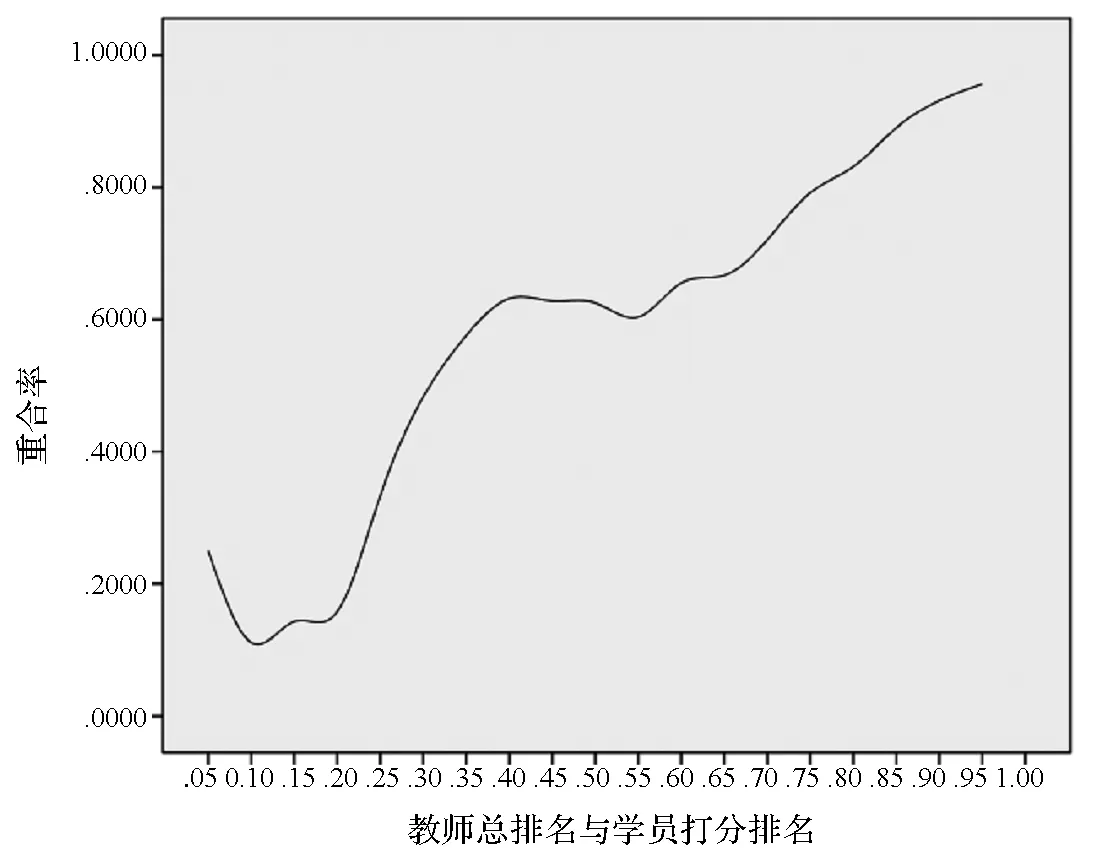
图4　教师总排名与学生打分的教师排名

五、专家与学生评教数据的Kappa一致性分析

教师课堂教学评价的总评分是学生评分和专家评分的加权平均值(本文中假设是各占百分之五十)，90(含)以上为评价优秀。在对参与评优的教师中，有些教师的总评分达到90分以上，但是在学生评价中的排序比较靠后。在总评分中虽然已经考虑到学生评价的成分，但是为了进一步体现学生评价的重要性，对学生打分排名靠后的90分以上得分的教师进一步筛选，如果排名靠后，将从优秀名单中去掉。问题是，学生打分排名靠后的线如何划？也就是排名排在前多少百分比的教师作为评价优秀的必要条件。

下面我们用Kappa检验方法分五种情况进行讨论，即当学生评价分别排在前50%、60%、70%、80%、90%的教师作为评优的必要条件，看它们与总评分90分以上作为评优条件的一致性如何。根据本文第1节描述的Kappa模型，设N=97为总的评价样本总数，k为学生评分排名的前百分比值，例如排名前70%，表示教师的学生评分位于前70%以内。P1和P2分别表示被评价者总分90分(含)以上的样本数和学生评价排名前k的样本数，N1和N2分别是被评价者总分小于90分的样本数和学生评价排名未排到前k的样本数。显然P1+N1=P2+N2=N.

表2给出了用Kappa统计量计算得出的三个学期评价数据的一致性指标值。

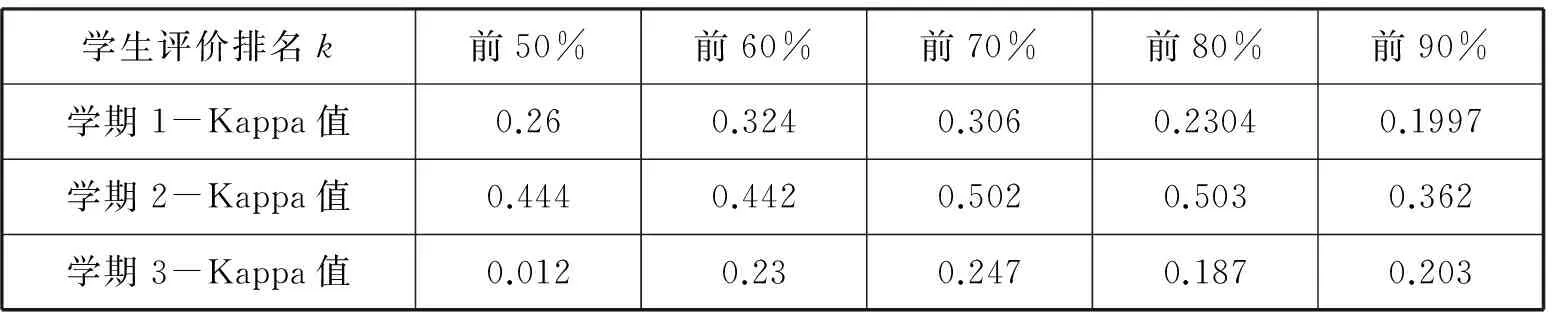
表2　学生评价排名与总评优秀的一致性程度

从计算结果看，Kappa值主要位于0.21-0.50之间，表明一致性是可接受的。这里的一致性，是计算总评分90分(含)以上的判断为优秀，90以下为良好以下，与学生评分排名前k为优秀，排名后k为良好的一致性。直观看，提高学生评价排名的百分比值，可以使得总评分为优秀与学生排名前k的重合率不断提高，评价优秀一致性不断提高，但同时增加了两者在非优秀(良好及其良好以下)评价的不一致性。因此从表2的数据中可以看出，评价优秀和良好以下的总一致性在学生排名前70%左右达到最大，之后又开始衰减。因此从数据分析角度看，取学生排名前70%左右作为一个判断优秀的必要条件是合理的。

六、结束语

教学督导组专家主要以随机采样方式从教学形式和教学内容对课堂教学进行评价。但是可能受到自身专业领域的限制，对授课专业内容不熟悉，难以对授课内容进行准确评价。虽然不是全程听课，但是根据采样理论，这种评价方式具有一定的合理性。

学生是教师授课的主体，他们是最直接的接受者，所以对教师的评价，他们最具有发言权。但是学生评教也有一定局限性的，体现在任务性、随意性、师生关系等。因此造成专家评价与学生评价的一致性存在某些偏差。

在考虑到专家评价与学生评价存在偏差的情况下，目前采用两者加权平均，总分超过90分的前提下，再次强调学生主体的重要性，以学生评价排名前70%作为优秀评价的必要条件，具有合理性。

今后还有许多工作可以研究，例如不同类型课程统一排名是否合理，理学、工科、文科、实验、核心与选修课程的统一排名是否合理？专家评价与学生评价的权重分别为多少合适？专家评价和学生评价的指标如何改进，专家采样评价和学生评价的方式是否进一步优化等问题，期待后续进一步开展研究。

[1]黄成林.国外教师教学质量评价发展的研究及启示[J].清华大学教育研究， 2006(6)：101-105.

[2]王宇柏.高等职业院校人才培养督导评价调研报告[J].北京市经济管理干部学院学报，2014(3)：53-59.

[3]周柏林.基于Kappa统计量的督导评教与学生评教一致性分析[J].科教导刊，2014(25)：3-5.

[4]冯静，潘正强，李国辉，等.基于非参数评价的课堂教学评价一致性建模与分析[J].数学的实践与认知，2015(15)：164-170.

(责任编辑：赵惠君)

A Consistency Analysis of Experts’and Students’Evaluation for Classroom Teaching

LI Guo-hui1，GENG Hui2，FENG Jing1，YANG Wen-yao1

(1.CollegeofInformationSystemandManagement，2.EducationDepartment，NationalUniversityofDefenseTechnology，Changsha410073，China)

Comprehensive evaluation combined with the experts’evaluation and the stadents’evaluation is an important method in the evaluation for classroom teaching.There rises a problem whether the experts’evaluation and the students’evaluation are consistent.Taking samples from the experts’evaluation and the students’evaluation in a certacn university，using desscriptive statistics，diagram analysis and Kappa statistic method，the paper analyses the consistency of both.

evaluation of classroom teaching；students’evaluation；experts’evaluation；consistency analysis

2016-05-31

李国辉(1963-)，男，湖南衡阳人。国防科学技术大学信息系统与管理学院教授，博士，主要从事信息系统工程研究。

G647

A

1672-8874 (2016) 03-0040-05