一个带有随机参数的新的二维混沌系统的随机Hopf分岔分析

罗瑞芬，张建刚，杜文举

(兰州交通大学数理学院，甘肃兰州 730070)



一个带有随机参数的新的二维混沌系统的随机Hopf分岔分析

罗瑞芬，张建刚，杜文举

(兰州交通大学数理学院，甘肃兰州 730070)

研究了一个带有随机参数的新的二维混沌系统的随机Hopf分岔.首先根据正交多项式逼近将此带有随机参数的二维混沌系统化为等价的确定性系统，然后通过第一Lyapunov系数法研究了等价的确定性系统的Hopf分岔.研究发现，随机系统与确定性系统不同，随机Hopf分岔的临界值不仅是由随机系统中的确定性参数决定，随机参数的强度也是决定因素之一.最后，理论结果通过数值模拟被证实.

稳定性；随机混沌；随机Hopf分岔；Chebyshev多项式逼近

Hopf分岔一直是非线性动力学领域中的一个研究热点，特别是近几年，许多学者对不同系统的Hopf分岔现象进行了较为深入的研究，涉及的领域也非常广泛，有化学工厂[1]、机械系统[2]、生态系统[3]、金融系统[4-5]、生物系统[6-7]、计算机网络[8-9]等.由于系统的复杂性，这些研究大体上仅限于定性阶段，对于系统的定量研究还相当有限，特别是对随机分岔的研究还处于初始阶段.随机系统在自然界中广泛存在，越来越多地被用来刻画事物间的动态关系，尤其是含有随机参数的随机系统.目前，解决含有随机参数的系统问题，有三个数学方法比较常用：蒙特卡罗方法[10]、随机微扰法和正交多项式逼近法[11]，其中第三种方法后来由Li[12]做了改善，是个有效的分析方法[13].近几年，利用Chebyshev多项式逼近法对一些经典的动力学模型的随机分岔和混沌现象[13-16]进行了成功的分析.Fang[17]运用Chebyshev多项式逼近法研究了有界随机变量的随机参数系统，李永坤等也运用此方法研究了随机动力系统的分岔与混沌现象以及控制和同步问题[18-22]，结果表明，Chebyshev多项式逼近法是研究含有随机参数的随机动力学问题的有效方法.本文用相同的方法对一个新的二维混沌系统的随机混沌和Hopf分岔进行了研究，并借助Maple软件详细讨论了这个系统的Hopf分岔现象，给出了这个系统产生Hopf分岔的参数条件.该方法对分析其它系统的Hopf分岔现象具有一定的参考意义.

1 一个带有随机参数的新的二维混沌系统的正交多项式逼近

确定性的二维混沌系统：

相应的方程（3）选择第二类切比雪夫多项式[16].ρU(u)表示第i个正交多项式，M表示选取多项式的最大阶数，同时正交多项式的正交性能可表达成如下形式：

的正交性，可以得到等价的确定性系统.当M →∞，方程（5）严格成立，否则方程（5）就是个近似方程.本文中取2M=，可得等价确定性的近似方程如下：

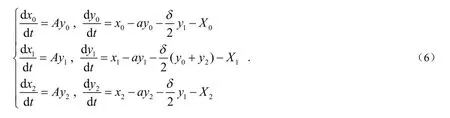
2 随机Hopf分岔分析

2.1 Hopf分岔的存在性

借助Maple，获得特征方程如下：

2.2 分岔的趋势和稳定性

为了进一步研究Hopf分岔，对系统（6）的第一Lyapunov系数进行研究.

当 L1＜0时，平衡点渐进稳定，发生超临界的Hopf分岔，并且在平衡点附近存在稳定的极限环；当 L1＞0时，平衡点不稳定，发生亚临界的Hopf分岔，并在平衡点附近存在不稳定的极限环.

令Cn是一个定义在复数域C上的非线性空间，p, q∈Cn，其中q∈Cn是特征值 Ρ1所对的特征向量，p∈Cn是一个伴随特征向量，满足：

当a=a0时，方程（6）有平衡点 o(0， 0， 0， 0， 0， 0)，方程（6）能表达成：

这里的x=(x0,y0, x1, y1, x2,y2)，B(x, y)，C（x, y, z）分别是双线性和三线性函数，可表示为：

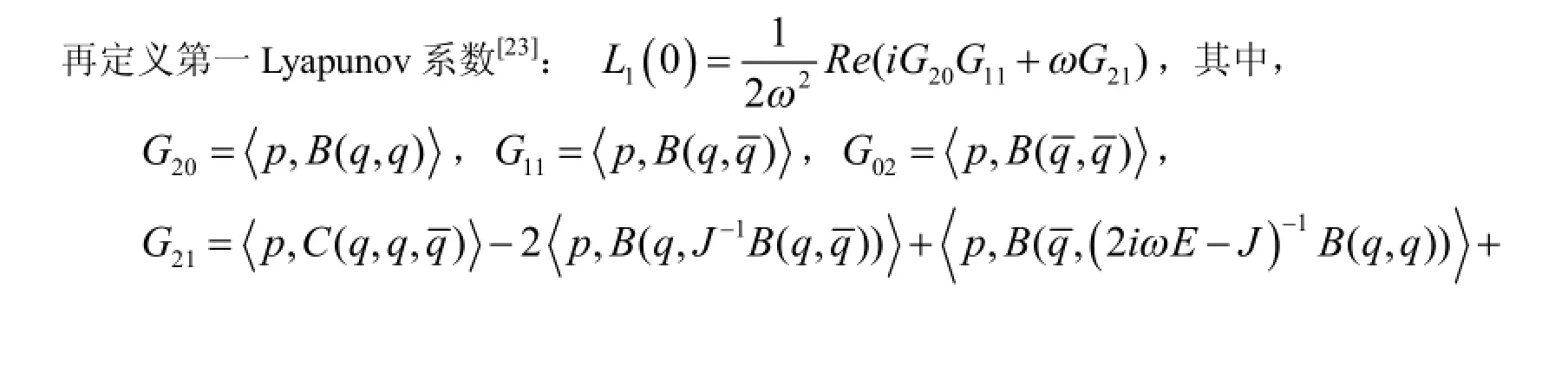
这里的K见附录.也可得到：

并且有：

3 结 语

本文通过正交多项式逼近来研究含有随机参数的二维混沌系统的随机Hopf分岔现象，利用正交多项式逼近将随机二维混沌系统化为等价的确定性系统，然后运用Lyapunov系数法对等价的确定性系统的Hopf分岔进行研究.结果表明，随机二维混沌系统中的随机Hopf分岔与传统的Hopf分岔不同，随机Hopf分岔的临界值不仅是由随机系统中的确定性参数决定，随机参数的强度也是决定因素之一.有关该系统在控制和同步方面的一些问题还需要进一步研究.

[1] Continillo G, Grabski A, Mancusi E, et al. Parallel tools for the bifurcation analysis of large-scale chemically reactive dynamical systems [J]. Computers Chemical Engineering, 2012, 38: 94-105.

[2] Walter V W. Stability and bifurcation in multi-scaled stochastic mechanic [J]. Procedia IUTAM, 2013, 6: 169-179.

[3] Huang D, Wang H. Hopf bifurcation of the stochastic model on HAB nonlinear stochastic dynamics [J]. Chaos, Solitions and Fractals, 2006, 27: 1072-1079.

[4] Zhang Q, Xu Z Z, Feng T J, et al. A dynamic stochastic frontier model to evaluate regional efficiency: Evidence fromChinese county-level panel data [J]. European Journal of Operational Research, 2015, 241: 907-916.

[5] Klaus B, Klijn F, Walzl M. Stochastic stability for roommate markets [J]. Journal of Economic Theory, 2010, 145: 2218-2240.

[6] Vinals J, Lepine F, Gaudreault M. Pitchfork and Hopf bifurcations in stochastic regulatory networks with delayed feedback [J]. Biophysical Journal, 2009, 96: 305.

[7] Hasegawa H. Stochastic bifurcation in FitzHugh-Nagumo ensembles subjected to additive and/or multiplicative noises [J]. Physica D, 2008, 237: 137-155.

[8] Li W, Su H, Wang K. Global stability analysis for stochastic coupled systems on networks [J]. Automatica, 2011, 47: 215-220.

[9] Huang Z T, Yang Q G, Can J F. The stochastic stability and bifurcation behavior of an Internet congestion control model [J]. Mathematical and Computer Modelling, 2011, 54: 1954-1965.

[10] Zhao H Y, Huang X X, Zhang X B. Hopf bifurcation and harvesting control of a bioeconomic plankton model with delay and diffusion terms [J]. Physica A, 2015, 421: 300-315.

[11] Zhang Y, Xu W, Fang T. Stochastic Hopf bifurcation and chaos of stochastic Bonhoeffer-vander Pol system via Chebyshev polynomial approximation [J]. Applied Mathematics and Computation, 2007, 190: 1225-1236.

[12] Li J. The expanded order system method of combined random vibration analysis [J]. Acta Mechanica Sinica, 1996, 28: 63-68.

[13] Ma S J. The stochastic Hopf bifurcation analysis in Brusselator system with random parameter [J]. Applied Mathematics and Computation, 2012, 219: 306-319.

[14] Pandey R K, Suman S, Singh K K, et al. An approximate method for Abel inversion using Chebyshev polynomials [J]. Applied Mathematics and Computation, 2014, 237: 120-132.

[15] Eslahchi M R, Dehghan M, Amani S. The third and fourth kinds of Chebyshev polynomials and best uniform Approximation [J]. Mathematical and Computer Modelling, 2012, 55: 1746-1762.

[16] Ma S J, Xu W, Li W, et al. Period-doubling bifurcation analysis of stochastic van der Pol system via Chebyshev polynomial approximation [J]. Acta Physica Sinica, 2005, 54: 3508-3515.

[17] Fang T, Leng X L, Song C Q. Chebyshev polynomials approximation for dynamical response problem of random system [J]. Journal of sound and vibration, 2003, 226:198-206.

[18] Li Y K, Li C Z. Stability and Hopf bifurcation analysis on a delayed Leslie-Gower Predator-prey system incorporating a prey refuge [J]. Applied Mathematics and Computation, 2013, 219: 4576-4589.

[19] Hu Z Y, Teng Z D , Zhang L. Stability and bifurcation analysis in a discrete SIR epidemic model [J]. Mathematics and Computers in Simulation, 2014, 97: 80-93.

[20] Anton C, Deng J, Wong Y S. Hopf bifurcation analysis of an aeroelastic model using stochastic normal form [J]. Journal of Sound and Vibration, 2012, 331: 3866-3886.

[21] Zhang G D, Shen Y, Chen B. Bifurcation analysis in a discrete differential-algebraic Predator-prey system [J]. Applied Mathematical Modelling, 2014, 38: 4835-4848.

[22] Wang B. Existence, stability and bifurcation of random complete and periodic solutions of stochastic parabolic equations [J]. Nonlinear Analysis, 2014, 103: 9-25.

[23] Hassard B, Kazarinoff N, Wan Y. Theory and Application of Hopf bifurcation [M]. Cambridge: CambridgeUniversity Press, 1981: 306-319.

附录：

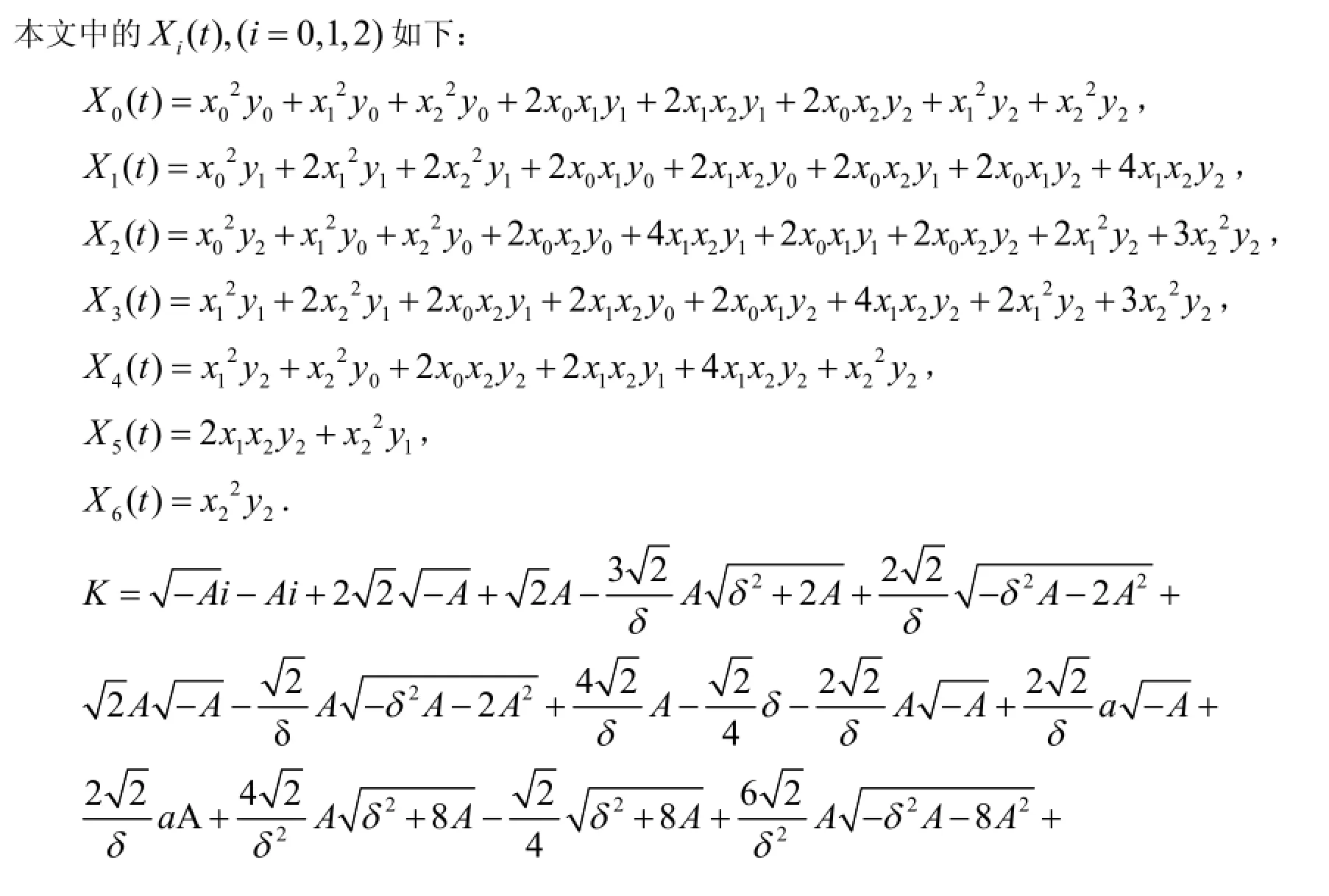
(编辑：王一芳)

Stochastic Hopf Bifurcation Analysis of a Novel Two-dimensional Chaotic System with Random Parameters

LUO Ruifen, ZHANG Jiangang, DU Wenju
(School of Mathematics and Physics, Lanzhou Jiaotong University, Lanzhou, China 730070)

It is probed in this paper that a novel two-dimensional chaotic system with random parameter is proposed. First of all, the system is trasformed from two-dimensional chaotic system with stochastic parameters to the equivalent deterministic system based on orthogonal polynomials approximation. Then the Hopf bifurcation of equivalent deterministic system is studied by the calculation of the first Lyapunov coefficient method. It is discovered from the research that the stochastic system differs from the deterministic system. The critical value of stochastic Hopf bifurcation is determined not only by deterministic parameters but also the intensity of random parameters in stochastic system which is one of the decisive factors. Finally, the numerical simulations results show the effectiveness of the method and the correctness of the theoretical results in the paper.

Stability; Stochastic Chaos; Stochastic Hopf Bifurcation; Chebyshev Polynomial Approximation

O175.12

A

1674-3563(2016)01-0026-10

10.3875/j.issn.1674-3563.2016.01.004 本文的PDF文件可以从xuebao.wzu.edu.cn获得

2015-05-07

罗瑞芬(1990- )，女，甘肃临夏人，硕士研究生，研究方向：随机动力学