水泥稳定碎石拉压弯静态模量与动态模量比较分析

吕松涛，陈杰东，张　晖

(长沙理工大学　公路养护技术国家工程实验室,湖南　长沙　410114)



水泥稳定碎石拉压弯静态模量与动态模量比较分析

吕松涛，陈杰东，张晖

(长沙理工大学公路养护技术国家工程实验室,湖南长沙410114)

为了揭示水泥稳定碎石半刚性基层材料的动、静态抗拉模量、抗压模量和弯拉模量之间的相关关系，开发了同时测试3种模量的新方法，推导出了在四点弯曲受力状态下水泥稳定碎石中的抗拉模量、抗压模量和考虑剪切效应影响的弯拉模量计算公式，开展了不同加载频率下的动态模量和加载速率为1 mm/min条件下静态模量的测试试验；揭示了水泥稳定碎石动态模量随加载频率的变化规律，建立了动、静态模量的转化关系，揭示了拉、压、弯3种动、静态模量的差异性。研究结果表明：水泥稳定碎石材料不是各向同性材料，呈现出明显的拉、压模量不同的特性；3种动态模量均随加载频率的增长呈现幂函数增长规律，动态模量试验条件更加符合路面实际受力状态；相同荷载级位下，3种动态模量都大于对应的静态模量，比值区间约为：1.11～1.91。

道路工程；水泥稳定碎石；室内试验；动态模量；静态模量；加载频率

0　引言

我国半刚性基层材料回弹模量的测定多以静态试验为主，静态试验方法中试件受力状态与路面结构真实应力状态差异较大，不能真实反映重复荷载作用下基层材料的动态响应性质。采用动态试验方法进行材料模量测试势必将成为我国路面结构设计的发展趋势[1-3]。另一方面，经典弹性理论描述的是拉伸、压缩弹性模量相同的材料，而在工程实际中，许多材料如混凝土等表现出拉、压不同的材料性质已成为大家的共识[4-6]。同样，半刚性基层是拉、压模量差异较大的结构层，我国在进行沥青路面结构设计时简单采用无侧限抗压回弹模量来进行结构的荷载响应分析[7-8]，造成计算结果与实际情况存在较大的偏差。在路面结构设计时如不考虑以上两方面因素，势必导致设计精度的降低，亦无法准确把握交通荷载作用下路用性能的衰变规律，导致养护决策的盲目性。

本文利用材料试验系统MTS(Material Test System)，提出了一种拉、压、弯拉模量同步测试的新方法，开展了不同加载频率下水泥稳定碎石动态弯拉模量、抗压模量、抗拉模量和1 mm/min加载速率下3种静态模量的试验，揭示了3种动态模量随加载频率的变化规律，对比分析了3种动、静态模量之间的差异性，为优化我国沥青路面结构刚度设计参数提供了试验依据和理论支撑。

1　配合比设计与试件制作养生

1.1原材料

水泥：采用P·C32.5级水泥，对其进行细度检测、凝结时间测试、安定性检测以及抗折强度试验，得到其各项技术性质如表1所示。

表1　水泥技术指标Tab.1　Cement technical indexes

集料：采用某碎石厂生产的石灰岩集料，公称最大粒径为19 mm，原材料各项技术指标均满足规范规程要求。

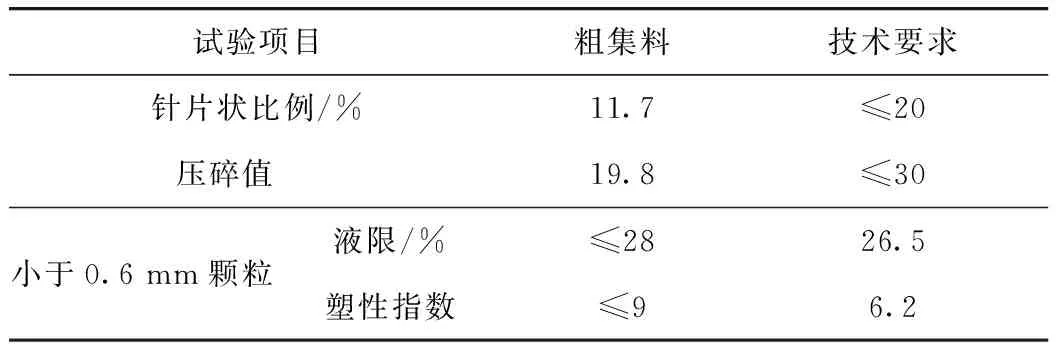
表2　集料性质试验结果Tab.2　Test result of aggregate property

1.2配合比试验

采用的矿料级配如表3所示。

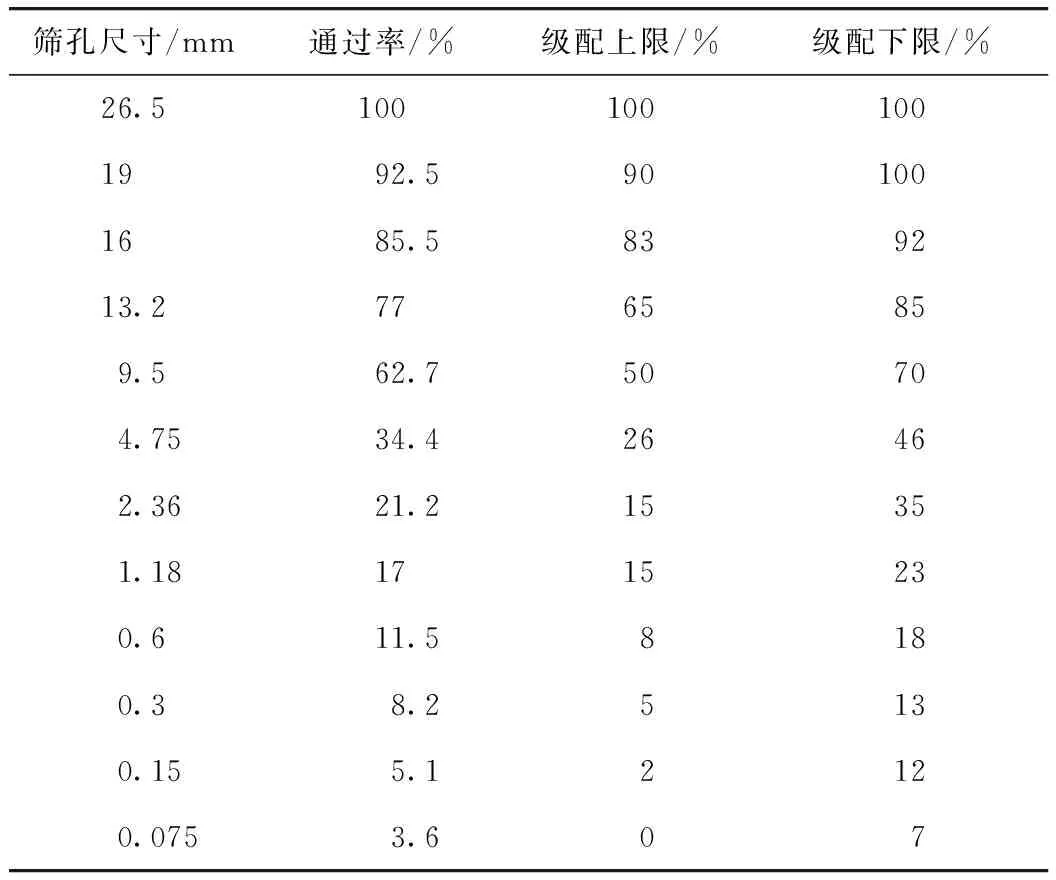
表3　水泥稳定碎石矿料合成级配Tab.3　Synthetic aggregate gradation of cement stabilized macadam

根据表3确定的矿料合成级配，进行水泥稳定碎石的重型击实试验，首先确定不同水泥剂量下的最佳含水量与最大干密度，而后通过各水泥剂量下的无侧限抗压强度试验确定满足要求的水泥剂量，最终试验结果为：水泥稳定碎石材料的外掺水泥剂量为4.5%，最大干密度为2.35 g/cm3，最佳含水量为4.5%。

1.3试件制备养生

据此，按照试验规程的要求[9]，制作弯拉强度及弯拉模量梁式试件，其尺寸为100 mm×100 mm×400 mm，试件成型均采用静压成型的试验方法，成型后，试件在温度为(20±2)℃、湿度≥95%的标准养生室内进行90 d标准龄期的养生。

2　模量试验方法与计算公式

2.1动静模量试验方法

路面材料静态模量是在逐级加、卸载条件下，根据材料受力和相应的回弹变形计算得出的模量。现行试验规程对于水泥稳定碎石材料弯拉模量的测试采用的是三分点加载的方式。将最大施加荷载(本论文采用极限破坏荷载的30%)均分为5～6级，持续稳定地施加第1级荷载的同时，利用LVDT位移计持续采集试件中部挠度变化，荷载施加时间为1 min；然后全部卸去荷载并保持0.5 min，让试件充分回弹，LVDT全程记录试件跨中挠度变化；之后逐级加载、卸载，得到多级荷载作用下的荷载-回弹变形曲线，加载、卸载速率均为1 mm/min。

在进行弯拉模量测试的基础上，在试验梁跨中上下表面分别对称粘贴4片应变片，共8片，并分别连接动态应变采集仪，以记录上表面的压应变和下表面的拉应变，用于抗压模量和抗拉模量的计算。由于水稳碎石试件表面一般比较粗糙，试验前需在粘贴应变片处用水泥浆填平表面缝隙，待水泥浆凝固后用砂纸打磨处理，避免水泥浆在试件表面成层。测试原理图和应变片粘贴方式分别如图1、图2所示。

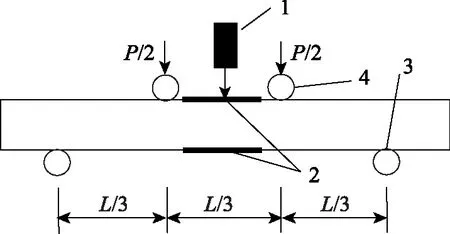
1—LVDT位移计；2—应变片；3—圆柱形支座；4—加载头图1　动静态拉压弯模量测试原理图Fig.1　Testing principle of tensile, compression, and flexural static and dynamic moduli

图2　应变片粘贴示意图Fig.2　Schematic diagram of strain gauges pasting

动态模量为材料在特定加载频率下受到荷载循环往复作用，根据对应的应力-应变关系计算得出的模量。其与静态模量测试方法的区别在于加载方式的不同，试验采用半正矢波加载，加载频率分为1，4，7，10 Hz 4个等级，荷载等级采用30%试件破坏荷载。荷载循环作用200次，取最后10次加载循环的平均荷载和变形振幅用于计算3种动态模量。

2.2动静模量计算方法

当梁的跨高比大于5时，纯弯曲的正应力公式可以推广应用于横力弯曲的正应力计算。然而对于跨高比小于5的试验梁，用材料力学细长梁的纯弯曲理论及假设计算时，误差会随高跨比减小而迅速增大[10]。现行无机结合料试验规程针对弯拉模量采用的是跨高比l/h为3的比例，并未考虑剪切作用对梁挠度的影响，故与实际情况不符[9]。本文在规程原公式的基础上，推导出了考虑剪切作用影响的弯拉模量计算修正公式(后文提及的弯拉模量均为考虑剪切影响后的弯拉模量)。

根据文献[9]，不考虑剪切影响的弯拉模量与跨中挠度存在以下关系：

(1)

式中，ω为跨中挠度；Ef为不考虑剪切影响的弯拉模量；P为施加荷载；L为试件跨径；b为跨中截面宽度；h为跨中截面高度。

当考虑剪切作用影响时，剪切作用引起的附加挠度在图1所示的四点弯曲试验条件下有

(2)

(3)

则弯、剪共同作用引起的挠度ω′可表示为：ω′=ω+Δω。将以上各式代入可得：

(4)

(5)

对于试件拉、压模量，文献[10]由平面假设和平衡条件，利用顶部压应变和底部拉应变得到了四点弯曲作用下，梁式试件的抗压模量、抗拉模量计算公式：

(6)

(7)

3　试验结果与分析

3.1动静态模量试验结果

针对3种静态模量进行5组试验分析，分析时泊松比μ取值0.25。计算分析结果如表4所示。

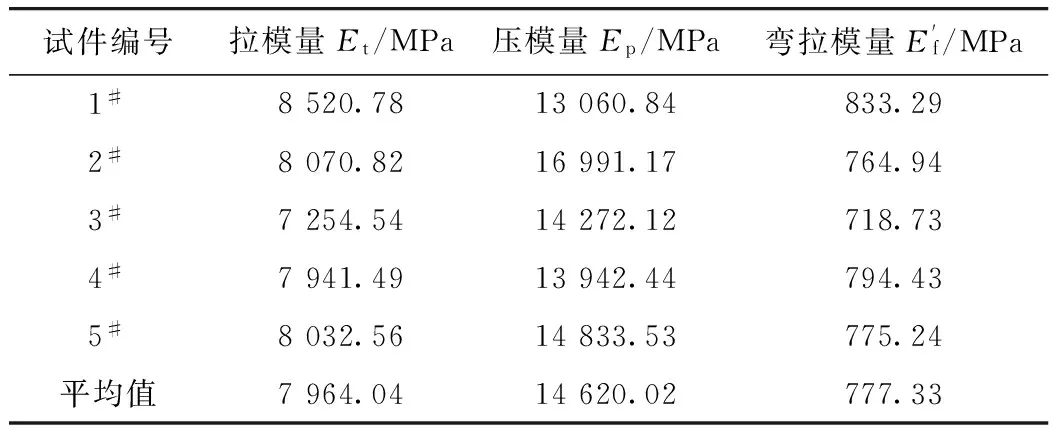
表4　静态拉压弯模量试验结果Tab.4　Test result of tensile, compression, and flexural static moduli

从表4可以看出：(1)拉模量均值为7 964 MPa，压模量均值为14 620 MPa，弯拉模量均值为777 MPa，压模量远远大于弯拉模量和拉模量，弯拉模量远远小于拉、压模量。(2)压模量与弯拉模量比值约为18.81，压模量与拉模量比值约为1.84，拉模量与弯拉模量比值约为10.25。这表明水泥稳定碎石材料是一种拉、压模量不同的各向异性材料。

实验室条件下的加载频率取决于外部荷载对路面结构的振动频率。现行半刚性材料动态模量测试借鉴国外经验，采用10 Hz的标准来表征车辆60～80 km/h速度下材料的受荷频率，然而对于其他车速对应的加载频率并未加以考虑，因此有必要开展不同加载频率下的动态模量测试，并揭示动静模量两者之间的对应关系。

不同加载频率下3种动态模量的测试结果如表5所示。

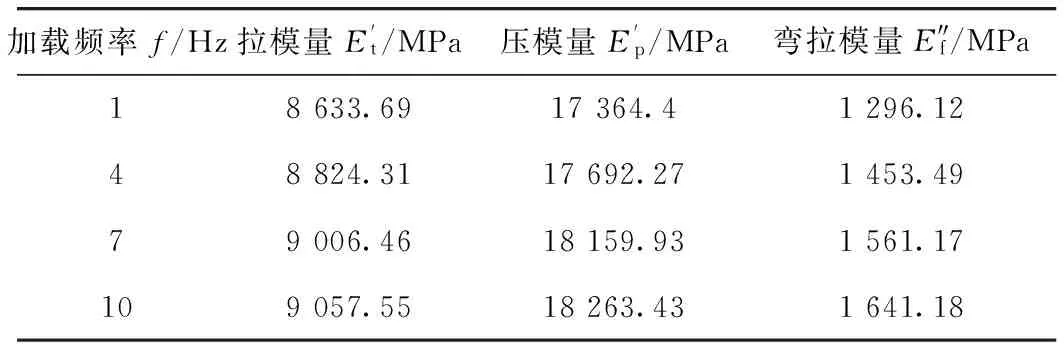
表5　不同加载频率下的动态拉压弯模量试验结果Tab.5　Test result of tensile, compression, and flexural moduli under different loading frequencies

由表5可看出，不同加载频率下压模量与弯拉模量比值分别为：13.40，12.17，11.63，11.13，比值均值为12.08；压模量与拉模量比值分别为：2.01，2.00，2.02，2.02，比值均值为2.01;拉模量与弯拉模量比值分别为：6.66，6.07，5.77，5.52，比值均值6.01。在动态荷载下，压模量亦远远大于拉模量和弯拉模量，水泥稳定碎石仍然表现出明显的拉、压模量不同的力学性质。

3种动态模量随加载频率的变化规律可用幂函数表征。同时，因为静态模量测试时，对应的加载频率应接近于0。因此，将静态模量视为加载频率为0时的取值考虑其中，得到了更为普适的模量-加载频率经验关系：

(8)

式中，E为动态拉、压、弯模量；E0为静态拉、压、弯模量；f为加载频率；a，b为拟合参数。

拟合过程如图3所示。

拟合结果汇总见表6。

研究表明造成动态模量增长的原因是多样的：有材料自身因素的影响，如试件本身压密成型，存在进一步的压紧密实的过程，导致在循环荷载作用下回弹变形的减小[12]；也存在试验条件的影响，在相同荷载条件下，荷载作用频率越高，对材料造成的激振频率越快，试件来不及产生相应的变形，导致试件的实际变形与响应回弹变形存在的滞后现象[13]；另外试件与设备之间的摩擦也会导致试件的结构阻尼增大，即材料的黏性变形越来越大[14]，以上因素综合导致了动态模量的逐级增加。从以上拟合结果可见，随着加载频率的增长，水泥稳定碎石动态模量呈现出较好的幂函数增长规律。

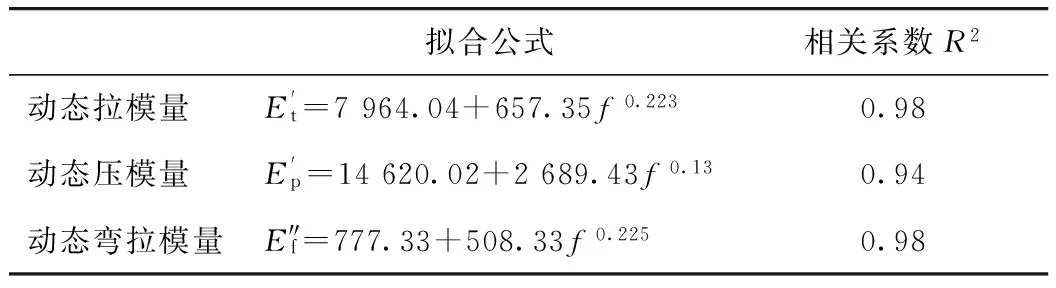
表6　不同加载频率下的3种动态模量拟合结果Tab.6　Fitting result of 3 dynamic moduli under different loading frequencies

3.2动静态模量比较分析

(1)静态荷载作用下的3种模量均小于加载频率为1 Hz下的动态模量，考虑到车速60～80 km/h的汽车荷载对应于10 Hz下的动态模量值，可见静态模量值不适合表征高速行驶车辆荷载作用下的路面真实受力状态，动态模量更能反映路面的实际情况。

(2)不同加载频率下动、静态压模量比值分别为：1.19，1.21，1.24，1.24，比值均值为1.22；拉模量比值分别为：1.08，1.11，1.13，1.14，比值均值为1.11；弯拉模量比值分别为：1.67，1.87，2.01，2.11，比值均值为1.91。这表明不同加载频率下，3种动态模量都大于静态模量，用静态模量分析路面结构力学响应是不合理的。

(3)从大量试验中可知路面常用材料在受力状态不同时，会表现出不同的应力-应变关系，即表现出不同的拉、压、弯模量特征。对于路面材料而言，早有学者提出路面设计中简单采用无侧限抗压回弹模量作为结构层模量的弊端，推导出了双模量理论的基本公式及试验方法[11]。从表4、表5的结果中可以看出，无论动态荷载还是静态荷载作用下，水泥稳定碎石材料的压模量都远远大于拉模量和弯拉模量，进一步佐证了水泥稳定碎石材料是一种拉、压模量不同的各向异性材料。这表明现规范用单一的无侧限抗压回弹模量来进行路面结构设计计算是不科学的，而应根据结构层不同位置所处的实际应力状态选用不同的模量类型。

4　结论

(1)水泥稳定碎石材料在动、静态荷载作用下，都表现出拉压模量不同的各向异性特性。用单一的静态模量来表征路面受力状态是不合适的，而应根据路面材料的实际受力状态选取相应的模量参数来进行结构应力分析。

(2)3种动态模量随加载频率的增长呈现幂函数增长关系。

(3)3种动态模量都大于静态模量，动、静态压模量比值约为1.22，拉模量比值约为1.11，弯拉模量比值约为1.91。动态模量更适合于分析路面结构在车辆荷载作用下的力学响应。

[1]沙爱民,贾侃,陆剑卿，等.半刚性基层材料动态模量的衰变规律[J].中国公路学报,2009,22(3):1-6.

SHA Ai-min,JIA Kan,LU Jian-qing，et al. Deterioration Laws of Dynamic Modulus of Semi-rigid Base Course Materials[J]. China Journal of Highway and Transport,2009,22(3):1-6.

[2]刘伟,严金海,李锋，等.乳化沥青冷再生混合料动静模量相关性[J].公路交通科技,2015,32(5):1-6.

LIU Wei,YAN Jin-hai,LI Feng, et al. Correlation between Dynamic Modulus and Static Modulus of Cold Recycled Mixture with Emulsified Asphalt [J]. Journal of Highway and Transportation Research and Development, 2015,32(5):1-6.

[3]孙建.沥青混合料动态模量研究[D].西安:长安大学，2007.

SUN Jian. Research on Dynamic Modulus of Asphalt Mixture[D]. Xi’an: Chang’an University,2007.

[4]张洪武,张亮，高强.拉压不同模量材料的参变量变分原理和有限元方法[J]. 工程力学,2012,29(8):22-17.

ZHANG Hong-wu, ZHANG Liang, GAO Qiang. The Parametric Variational Principle and Finite Element Method for Material with Different Modulus in Tension and Compression[J]. Engineering Mechanics, 2012,29(8):22-17.

[5]孔娟,袁聚云,潘晓明，等.不同拉压模量厚壁球壳弹塑性分析[J].力学与实践,2010,32(1):41-45.KONG Juan,YUAN Ju-yun,PAN Xiao-ming,et al. Elasto-plastic Analysis of Thick Spheric Shell with Different Elastic Moduli for Tensile and Compressive Deformations [J].Mechanics in Engineering, 2010,32(1):41-45.

[6]PATEL B P, KHAN K, NATH Y. A New Constitutive Model for Bimodular Laminated Structures: Application to Free Vibrations of Conical/Cylindrical Panels[J]. Composite Structures,2014,110(3):183-191.

[7]JTG D50—2006,公路沥青路面设计规范[S].

JTG D50—2006, Specifications for Design of Highway Asphalt Pavement[S].

[8]姚祖康.沥青路面结构设计[M].北京：人民交通出版社，2011.

YAO Zu-kang. Design of Asphalt Pavement Structure [M].Beijing: China Communications Press,2011.

[9]JTG E51—2009,公路工程无机结合料稳定材料试验规程[S].

JTG E51—2009, Test Methods of Materials Stabilized with Inorganic Binders for Highway Engineering [S].

[10]王中正,朱军祚,谌磊，等.集中力作用下深梁弯剪耦合变形应力计算方法[J].工程力学,2008,25(4):115-119.

WANG Zhong-zheng, ZHU Jun-zuo, CHEN Lei,et al. The Stress Caculation Method for Deep Beams with Shear-bending Coupling Distortion under Concentrated Load [J]. Engineering Mechanics, 2008,25(4):115-119.

[11]刘金莲,应荣华.双模量理论在柔性路面设计中的应用研究[J].湖南交通科技,2001,27(1):16-23.

LIU Jin-lian,YING Rong-hua. Application Research of Double Modulus Theory in Flexible Pavement Design[J].Hunan Communications Science and Technology,2001,27(1):16-23.

[12]程箭,许志鸿,李淑明，等. 水泥稳定碎石静态模量与动态模量比较[J].建筑材料学报,2009,12(1):63-75.

CHEN Jian,XU Zhi-hong,LI Shu-ming,et al. Comparison of Compressive Resilient Modulus and Dynamic Modulus of Cement-Stabilized Macadam[J].Journal of Building Materials, 2009,12(1):63-75.

[13]郭大进,黑鹏,韩立志.半刚性基层材料动态特性研究[J].公路交通科技,2005,22(12):42-61.

GUO Da-jin, HEI Peng, HAN Li-zhi. Study on Dynamic Characteristics of Semi-rigid Base Layer [J].Journal of Highway and Transportation Research and Development,2005,22(12):42-61.

[14]ORUC S, CELIK F, AKPINAR M V. Effect of Cement on Emulsified Asphalt Mixtures[J]. Journal of Materials Engineering & Performance, 2007, 16(5):578-583.

Comparative Analysis of Tensile, Compression, Flexural Static Modulus and Dynamic Modulus of Cement-stabilized Macadam

LÜ Song-tao，CHEN Jie-dong，ZHANG Hui

(State Engineering Laboratory of Highway Maintenance Technology, Changsha University of Science & Technology,Changsha Hunan 410114, China)

In order to reveal the relations of tensile, compression and flexural resilient moduli with dynamic moduli of cement-stabilized macadam semi-rigid base, a new test method for measuring 3 moduli simultaneously is developed. The formulas of tensile, compression, and flexural modulus which considering the influence of shearing effect for cement-stabilized macadam under 4-point bending are derived. The measurment experiments of dynamic modulus under different loading frequencies and static modulus at 1 mm/min loading speed are conducted. The change rules of tensile, compression and flexural moduli with loading frequency are revealed, and the transformation relationships of static and dynamic moduli are established. The differences of tensile, compression and flexural static modulus and dynamic modulus are revealed. The result indicates that (1) cement-stabilized macadam is not isotropic material, the tensile and compression moduli show a significant difference obviously; (2) the variations of 3 dynamic moduli show a power function growth relationship with the increase of loading frequency, the testing condition of dynamic modulus is closer to the actual stress condition of the pavement; (3) three dynamic moduli are larger than the corresponding static modulus under the same load level, the ratio range is from 1.11 to 1.91 approximately.

road engineering; cement stabilized macadam; laboratory test; dynamic modulus; static modulus; loading frequency

2015-11-12

国家自然科学基金项目(51208066，51578081)

吕松涛(1979-)，男，河南郑州人，博士,副教授.(58003611@qq.com)

10.3969/j.issn.1002-0268.2016.10.007

U416.217

A

1002-0268(2016)10-0039-05