顾及最小二乘拟合端点效应的日长变化预报*
2016-10-27蔡宏兵
雷 雨,蔡宏兵
(1. 中国科学院国家授时中心,陕西 西安 710600;2. 中国科学院时间频率基准重点实验室,陕西 西安 710600;3. 中国科学院大学,北京 100049)
顾及最小二乘拟合端点效应的日长变化预报*
雷雨1,2,3,蔡宏兵1,2
(1. 中国科学院国家授时中心,陕西 西安710600;2. 中国科学院时间频率基准重点实验室,陕西 西安710600;3. 中国科学院大学,北京100049)
针对日长(Length Of Day, LOD)变化预报中最小二乘(Least Squares, LS)拟合存在端点效应的问题,采用时间序列分析方法对日长变化序列进行端点延拓,形成一个新序列,然后用新序列建立最小二乘模型,最后再结合最小二乘模型和自回归(Autoregressive, AR)模型对原始日长变化序列进行预报。实验结果表明,在日长变化序列两端增加统计延拓数据,能有效减小最小二乘拟合序列的端点畸变,从而提高日长变化的预报精度,尤其对中长期预报精度提高明显。
日长变化;预报;最小二乘拟合;端点效应;时间序列分析
日长变化是表征地球自转运动的一个重要参量,反映了地球自转速率的快慢。日长变化与极移(Polar Motion, PM)的两个分量统称为地球自转参数(Earth Rotation Parameters, ERP)。地球自转参数是实现地球参考系与天球参考系相互转换的必需参数,在卫星导航、深空探测以及天文地球动力学研究等领域有重要应用[1]。卫星激光测距(Satellite Laser Ranging, SLR)、甚长干涉基线测量(Very Long Baseline Interferometry, VLBI)与全球卫星导航系统(Global Navigation Satellite System, GNSS)等现代空间测地技术是获取地球自转参数的主要手段,但复杂的资料处理过程使得地球自转参数的获取存在一定延迟,因此对地球自转参数进行高精度预报是一项必要工作。
当前预报日长变化的方法有多种,这些方法大多是最小二乘外推模型和其他模型的组合,如最小二乘外推与自回归(Autoregressive, AR)模型的组合(LS+AR)[2]、最小二乘外推与神经网络(Neural Network, NN)技术的组合(LS+NN)[3-5]和最小二乘外推与高斯过程回归(Gaussian Process Regression, GPR)模型的组合(LS+GPR)[6-7]等。这些组合方法均是首先建立最小二乘外推模型,得到日长变化序列趋势项和周期项的外推值,再利用其他方法对最小二乘拟合残差序列进行预报,而日长变化预测值为最小二乘外推值和残差序列预测值的叠加。
实际工作中发现,在利用最小二乘模型对日长变化序列进行拟合时,在拟合序列的两端存在发散畸变现象(在数据处理中称作端点畸变效应,简称端点效应),致使趋势项、周期项和残差序列的预报值出现偏差,最终导致日长变化序列的最终预测值不准确。本文针对日长变化预报中最小二乘拟合存在端点效应的问题,在利用最小二乘模型拟合日长变化序列之前,先采用时间序列分析方法对日长变化序列进行数据延拓,即在观测序列的两端增加用统计学方法延拓出的若干数据点,形成一个新序列,然后用新序列求得最小二乘模型系数,最后再利用最小二乘外推与自回归组合模型对日长变化原始序列进行预测。算例表明,通过对观测序列两端的数据延拓,可以有效消除端点效应的影响,从而提高日长变化预报的精度。
1 预报方法
1.1资料预处理
本文所用日长变化资料源自国际地球自转与参考系服务(International Earth Rotation and Reference Systems Service, IERS)组织发布的EOP 05 C04序列,采样间隔为1 d。日长变化序列中包含多种周期性变化成分,其中对周期为5 d~18.6 a的62个固体地球带谐潮汐项利用IERS协议给出的经验模型给予扣除[8],而扣除这些固体潮汐项后的日长变化称为ΔLODR。本文对日长变化的预报均是针对ΔLODR的预报。
1.2最小二乘外推模型
日长变化序列扣除固体潮汐项后,还含有长期趋势项和周年项、半周年项等季节性变化成分,这些趋势项和周期项采用下述最小二乘模型进行拟合和外推:
(1)
其中,T1和T2分别表示周年项和半周年项的振荡周期,本文取T1=365.24 d、T2=182.62 d;a和b表示长期趋势项参数;c1和d1表示周年项参数;c2和d2表示半周年项参数。这6个未知参数可以通过最小二乘法求得。
1.3自回归模型
自回归模型是对平稳时间序列{zt,t=1, 2, …,n}建立的一个概率统计模型,它根据变量自身过去的变化规律来建立预报模型,其数学模型为
(2)
其中,p为模型阶次;εt为白噪声;φ1,φ2, …,φp为模型参数,可以采用Yule-Walker方程求解。
使用自回归模型的关键在于选取模型阶次p。常用的定阶准则有信息论准则、传递函数准则与最终预报误差准则,这3种准则在实际应用中是等效的[9]。本文选用赤池信息量准则(Akaike Information Criterion, AIC)确定阶次p,准则函数可以表示为
(3)
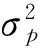
当模型阶次p和模型参数φ1, φ2, …, φp确定时,可根据下述方式进行时间序列的多步外推预报。
(4)
(5)
(6)
1.4预报流程
本文预报方法与常规方法的区别在于,本文方法在对ΔLODR序列建立趋势项和周期项最小二乘外推模型之前,首先利用时间序列分析方法在ΔLODR序列首尾两端进行数据延拓,以削弱最小二乘拟合端点效应的影响,具体方法如下:
(1)首先根据(1)式对ΔLODR序列进行最小二乘拟合,建立趋势项和周期项外推模型,然后利用自回归模型对最小二乘残差序列进行预报,最后利用最小二乘外推与自回归组合模型在ΔLODR序列首尾两端分别外推若干数据点,这样原始ΔLODR序列加上首尾两端外推的数据形成了一个新序列。
(2)利用新序列确定最小二乘模型系数,即用新序列重新建立趋势项和周期项最小二乘外推模型,然后再结合最小二乘模型和自回归模型对原始ΔLODR序列进行预报。
需要说明的是,新序列只用来求解最小二乘模型系数,而在后续预报中仍然使用原始ΔLODR序列。
2 算例分析
选用1999年1月1日至2011年10月22日期间的日长变化数据进行实验,其中2010年1月1日至2011年10月22日作为预报期,建模序列长度取为10a。
为了验证端点数据延拓方法对端点效应的改善效果,首先对比端点延拓前后最小二乘拟合效果。图1绘出了端点延拓前后最小二乘拟合的残差序列,其中图1(a)为最小二乘拟合序列首端前50个历元的残差序列,图1(b)为最小二乘拟合序列尾端最后50个历元的残差序列,拟合时段为2000年10月26日至2010年10月25日,端点延拓数据个数为360,即在首尾两端各外推360个数据点。
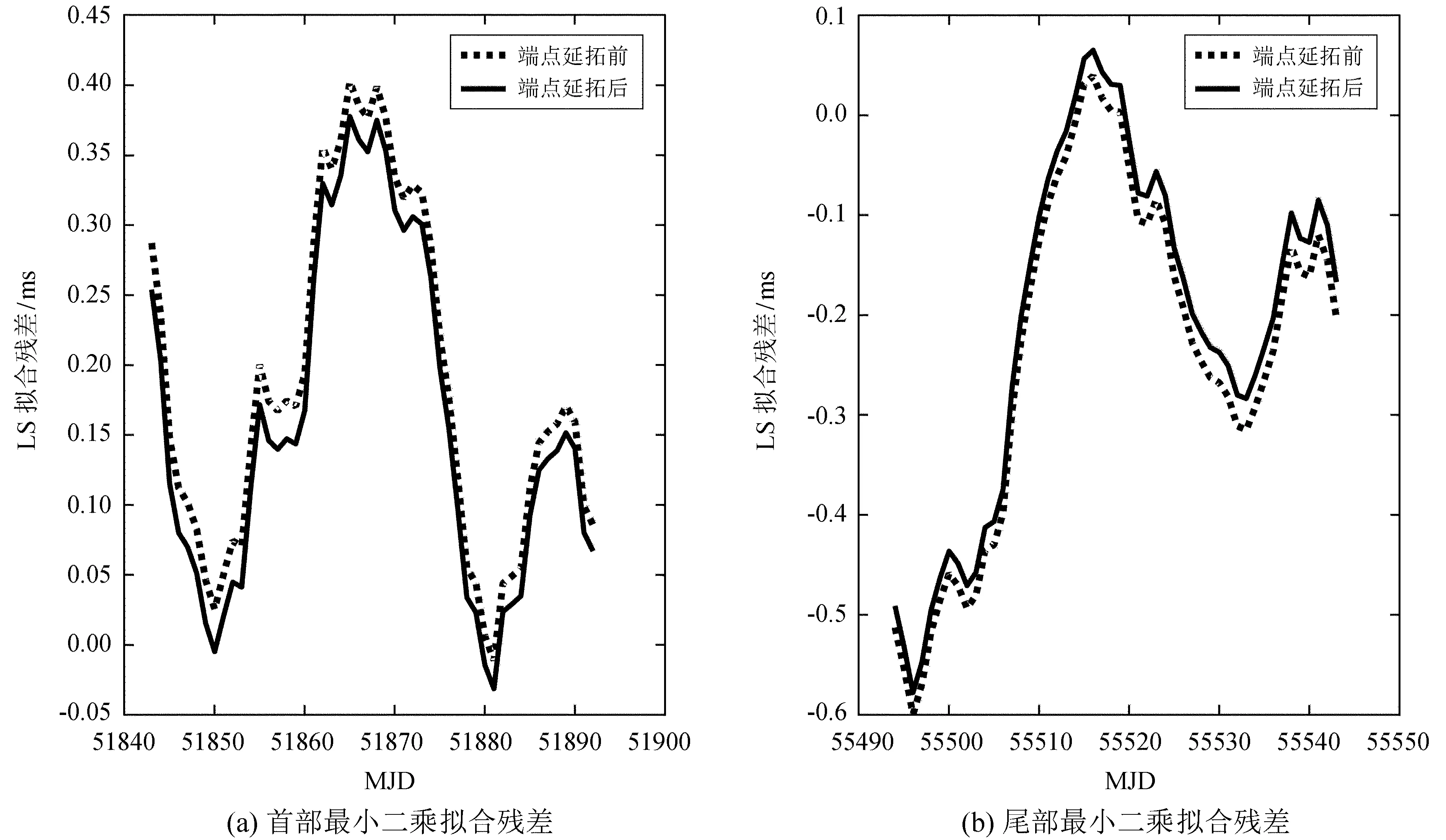
图1端点延拓前后最小二乘拟合效果对比
Fig.1ComparisonofLSfittingwithandwithoutedgeextension
从图1可以看到,与端点延拓前相比,端点延拓后最小二乘拟合残差在序列首尾两端更接近于0,即端点延拓后最小二乘拟合的ΔLODR序列更为准确,这说明端点延拓方法能有效抑制最小二乘拟合出现的端点效应问题。为了进一步说明端点延拓方法对端点效应的改善作用,本文选取1999年1月1日至2009年12月31日期间的日长变化数据进行拟合实验,将拟合长度取为10 a,每隔1 d拟合1次,即拟合滑动窗口为10 a,总共拟合300次,并统计每次端点延拓前后首部和尾部50个历元残差序列的均方根误差(Root Mean Square Error, RMSE),其中端点延拓前首部和尾部50个历元残差序列的300次平均均方根误差分别为0.29 ms和0.30 ms,端点延拓后首部和尾部50个历元残差序列的300次平均均方根误差分别为0.22 ms和0.23 ms,实验结果可以说明端点延拓方法对端点畸变的抑制效果。
为了验证本文方法相对于常规最小二乘外推与自回归组合模型对日长变化预报精度的改善情况,分别利用这两种方法对日长变化进行1~360 d跨度预报,选用均方根误差作为精度评估指标,其计算公式为
(7)
其中,Pj、Oj分别表示j点的日长变化预测值和观测值;l为预报跨度;N为预报期数。本文总共进行了300期的预报,每次预报时建模序列长度始终取为10 a,每隔1 d滑动预报1次,即N=300。
图2给出了本文方法和常规最小二乘外推与自回归组合模型的日长变化预报均方根误差对比图,表1统计了两种方法在各种跨度的预报均方根误差情况。结合图2和表1可以看出,本文方法的预报精度相对于常规最小二乘外推与自回归组合模型在各个预报跨度有不同程度的改善,其中,对于1~30 d短期预报,预报精度改善不明显,在10%以内;从第30 d开始,本文方法的预报精度明显优于常规最小二乘外推与自回归组合模型,精度最大改善了15.80%,且一直保持在13%左右,这说明本文方法对于中长期跨度预报具有更明显的优势,同时也从侧面说明端点效应对日长变化中长期预报的影响更大。
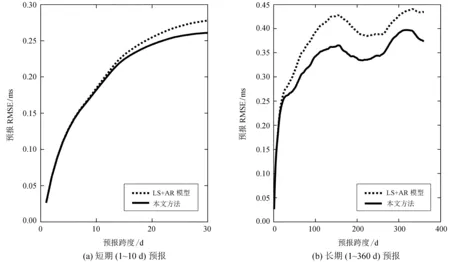
图2本文方法和常规最小二乘外推与自回归组合模型的日长变化预报均方根误差对比
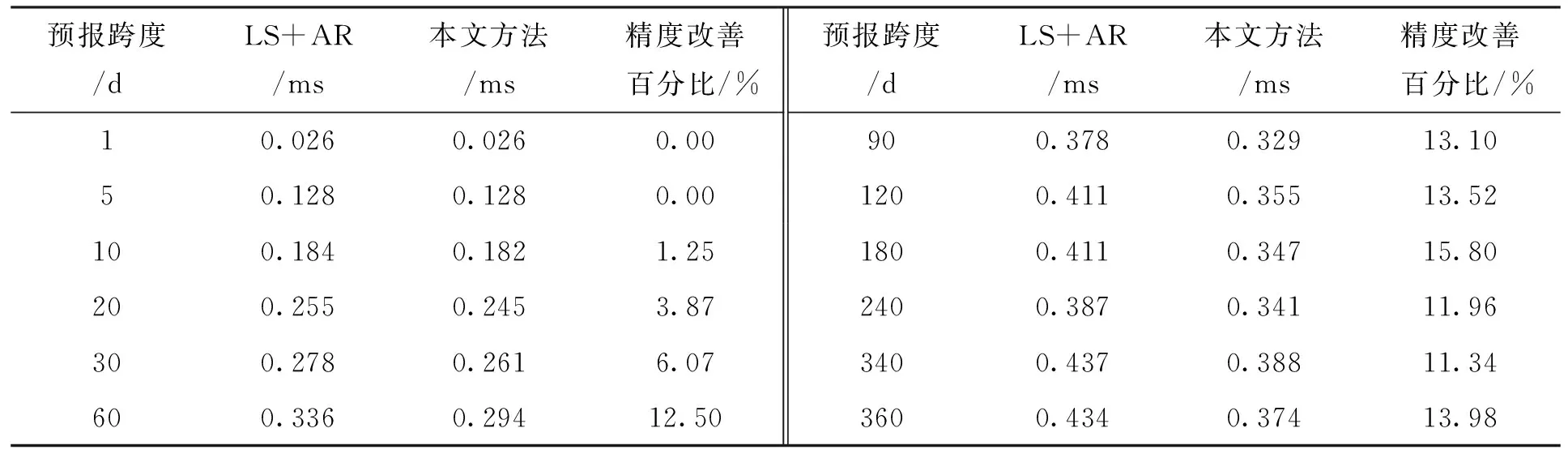
Fig.2 Comparison of the prediction RMSE between the LS+AR and the proposed method
3 结 论
本文提出了一种顾及最小二乘拟合端点效应的日长变化预报方法,其实质是在原始序列两端增加统计延拓数据,以将最小二乘拟合出现的端点效应移至模拟序列的两端,从而减小原始序列的端点畸变。算例表明,通过在观测序列的两端增加用时间序列分析方法延拓的模拟数据点,然后再进行最小二乘拟合,可以有效削弱端点效应的影响;相对于常规最小二乘外推与自回归组合预报模型,本文方法的日长变化预报精度有明显改善,对于中长期预报其精度提高尤为明显。此外,在实验中发现,端点延拓长度对本文方法的预报精度具有较大影响,本文对此并未进行深入研究,而仅仅选取了相对较优的预报结果,因此,本文方法仍有提升空间。对于如何选取最佳的端点延拓长度,将进行深入研究。
[1]Gambis D, Luzum B. Earth rotation monitoring, UT1 determination and prediction[J]. Metrologia, 2011, 48(4): 165-170.
[2]Xu Xueqing, Zhou Yonghong. EOP prediction using least square fitting and autoregressive filter over optimized data intervals[J]. Advances in Space Research, 2015, 56(10): 2248-2253.
[3]Wang Qijie, Du Yanan, Liu Jian. Introducing atmospheric angular momentum into prediction of length of day change by generalized regression neural network model[J]. Journal of Central South University, 2014, 21(4): 1396-1401.
[4]Lei Yu, Zhao Danning, Cai Hongbing. Prediction of length-of-day using extreme learning machine[J]. Geodesy and Geodynamics, 2015, 6(2): 151-159.
[5]雷雨, 蔡宏兵, 赵丹宁. 样本输入方式对极端学习机预报日长变化的影响[J]. 天文研究与技术, 2015, 12(3): 299-305.
Lei Yu, Cai Hongbing, Zhao Daning. Effects of training patterns on predictions of variations of length of day using an extreme learning machine neural network[J]. Astronomical Research & Technology, 2015, 12(3): 299-305.
[6]雷雨, 赵丹宁, 高玉平, 等. 基于高斯过程的日长变化预报[J]. 天文学报, 2015, 56(1): 53-62.
Lei Yu, Zhao Daning, Gao Yuping, et al. The prediction of length-of-day variations based on Gaussian processes[J]. Acta Astronomica Sinica, 2015, 56(1): 53-62.
[7]Lei Yu, Guo Min, Cai Hongbing, et al. Prediction of length-of-day using Gaussian process regression[J]. The Journal of Navigation, 2015, 68(3): 563-575.
[8]Petit G, Luzum B. IERS conventions (2010) [R]. Frankfurt am Main: Verlag des Bundesamts für Kartographie und Geodäsie, 2011: 123-131.
[9]丁月蓉, 郑大伟. 天文数据处理方法[M]. 南京: 南京大学出版社, 1998: 307-308.
Enhancing the Prediction Accuracy of the Length of Day Change by Eliminating the Edge-effect of Least Squares Fitting
Lei Yu1,2,3, Cai Hongbing1,2
(1. National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China, Email: leiyu@ntsc.ac.cn;2. Key Laboratory of Time and Frequency Primary Standards, Chinese Academy of Sciences, Xi’an 710600, China;3. University of Chinese Academy of Sciences, Beijing 100049, China)
In order to eliminate the edge-effect of least squares (LS) fitting for the length of day change (ΔLOD), the time-series analysis model is first used to extrapolate ΔLOD series forward and backward and then generate a new series. Subsequently, the cofficients of a LS model are estimated using the new generated series. As a result, the edge-effect is changed to the edge of the new series, and thus the original fitted ΔLOD series can be free from the edge-effect. Finally, a combination of LS and autoregressive (AR) models (LS+AR) is employed to predict the original ΔLOD data. The results indicate that the proposed method can efficiently eliminate the edge-effect, and thus improve the prediction accurcy of the LS+AR model, especially for medium- and long-term prediction.
Length Of Day (LOD) change; Prediction; Least Squares (LS) fitting; Edge-effect; Time-series analysis
中国科学院 “西部之光” 人才培养计划联合学者项目(201491) 资助.
2015-12-29;
2016-01-19
雷雨,男,博士. 研究方向:地球自转变化监测与预报. Email: leiyu@ntsc.ac.cn
P227.1
A
1672-7673(2016)04-0441-05
CN 53-1189/PISSN 1672-7673
