吊杆张拉程序对外倾单肋钢拱桥拱肋内力影响分析
2016-10-26汪一意陈建兵俞志豪
汪一意,陈建兵,俞志豪
(苏州科技大学土木工程学院,江苏苏州215011)
WANG Yiyi,CHEN Jianbing,YU Zhihao
(School of Civil Engineering,Suzhou University of Science and Technology,Suzhou 215011)
吊杆张拉程序对外倾单肋钢拱桥拱肋内力影响分析
汪一意,陈建兵,俞志豪
(苏州科技大学土木工程学院,江苏苏州215011)
以某外倾单肋异形钢拱桥为研究对象,采用有限元计算程序Midas/Civil建立空间有限元模型,对吊杆的张拉顺序、张拉次数对拱肋内力及拱肋吊点位移的影响进行了对比分析计算。考虑结构内力均衡与安全,兼顾施工方便性和经济性,得到了较为合理的张拉方案Ⅲ:交替对称一次张拉至最终吊杆力的张拉程序。
外倾单肋;钢拱桥;吊杆;张拉顺序;有限元分析
WANG Yiyi,CHEN Jianbing,YU Zhihao
(School of Civil Engineering,Suzhou University of Science and Technology,Suzhou 215011)
桥梁除了满足结构安全、经济适用外,桥梁艺术及美学也逐渐引起了人们的重视,一大批结构形式新颖、造型别致的桥相继建成[1]。外倾单肋式拱桥是区别于传统形式拱桥的新型拱桥[2],该桥的受力性能比较复杂,其拱肋的受力受施工因素影响较大,不同的吊杆张拉顺序会对拱桥结构受力产生不同的影响,有时会成为控制结构受力的关键因素[3-4]。目前,国内外专家学者对双肋外倾式拱桥的整体受力及钢结构的稳定分析进行了大量研究,但鲜见对施工过程中单拱肋的内力受不同吊杆张拉顺序影响的研究。本文结合某外倾单肋异形钢拱桥,根据各施工阶段情况提出了不同的吊杆张拉顺序,计算分析了不同的吊杆张拉顺序及次数对其拱肋内力的影响,得出了合理的吊杆张拉方案,为此类桥梁施工提供参考。
1 工程概况
本桥为三跨异形钢拱桥,全长131.93 m,跨径布置为12.5 m+105 m+12.5 m,桥宽5 m,中跨为105 m下承式异形钢拱桥,主梁为钢结构曲线箱梁;主跨和边跨道路平面均位于曲线范围,曲线半径分别为108 m和29.1 m;桥梁以跨中为对称中心,采用双向人字坡2.3%和-2.3%,竖曲线半径为434.7 m;桥梁立面及横断面图如图1、图2所示。拱肋向外倾斜15°,拱轴线在其自身倾斜面内为二次抛物线,矢高为26.25 m,矢跨比为1/4,拱肋截面采用矩形,全拱为变截面,截面宽度由拱脚的3.5 m变至拱顶的2.0 m,截面高度由拱脚的2.0 m变至拱顶的1.5 m。拱脚标准断面如图3所示,其中由拱脚向跨中方向6 m肋中灌注C40微膨胀混凝土。吊杆采用1860级环氧喷涂钢绞线,直径65 mm,水平布置间距为4.5 m,全桥合计19根吊杆。拱肋与主梁之间为刚性连接,如图4所示。全桥钢材均采用Q345钢。
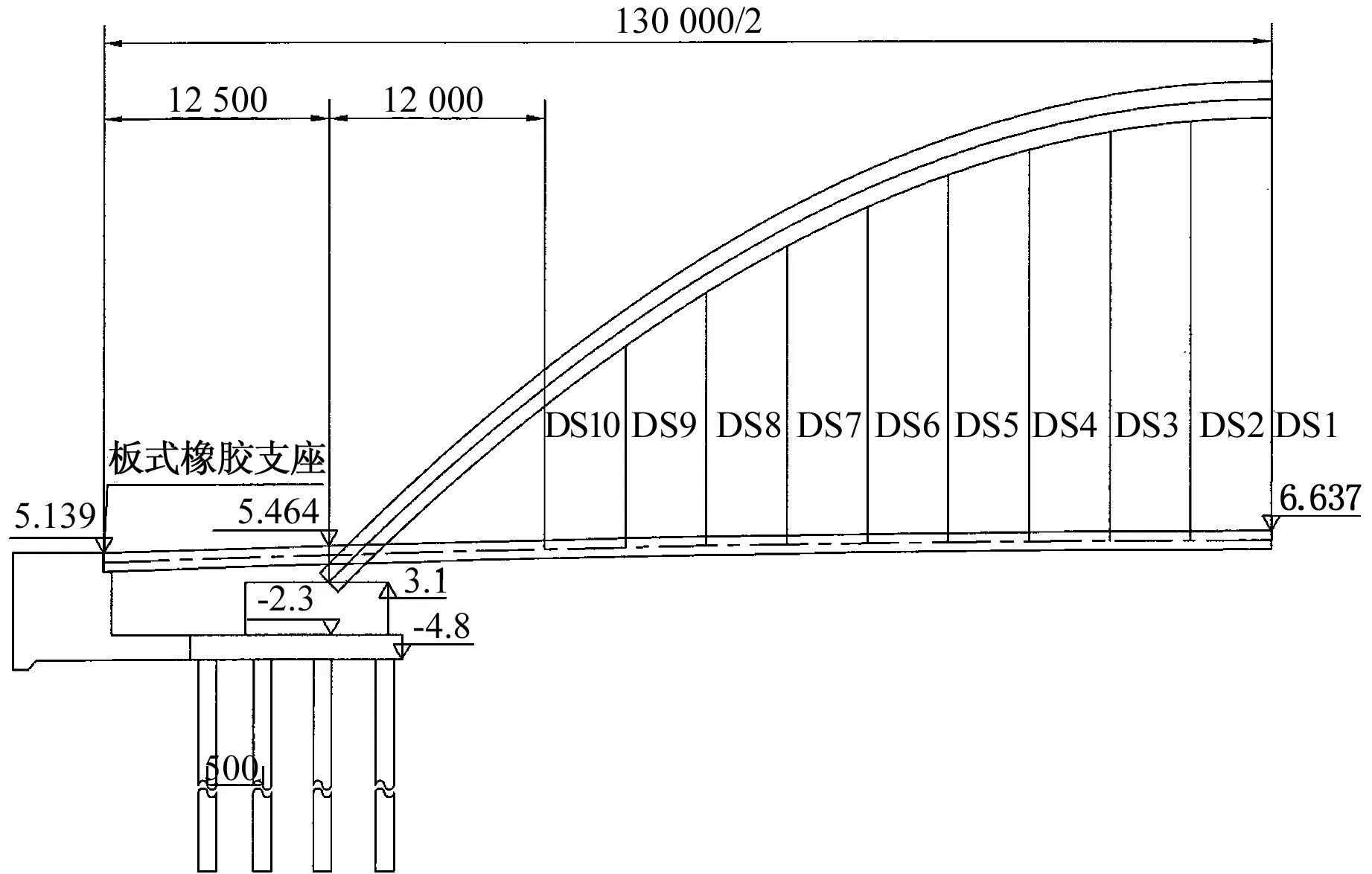
图1 桥梁立面图(单位:mm)
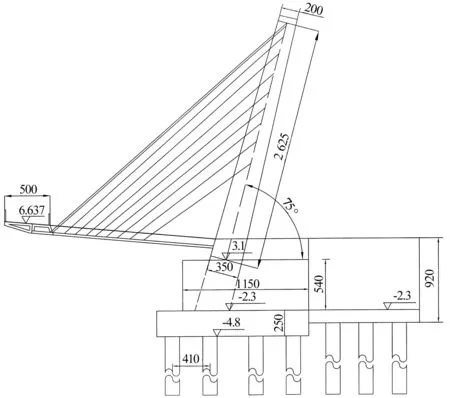
图2 桥梁横断面图(单位:cm)
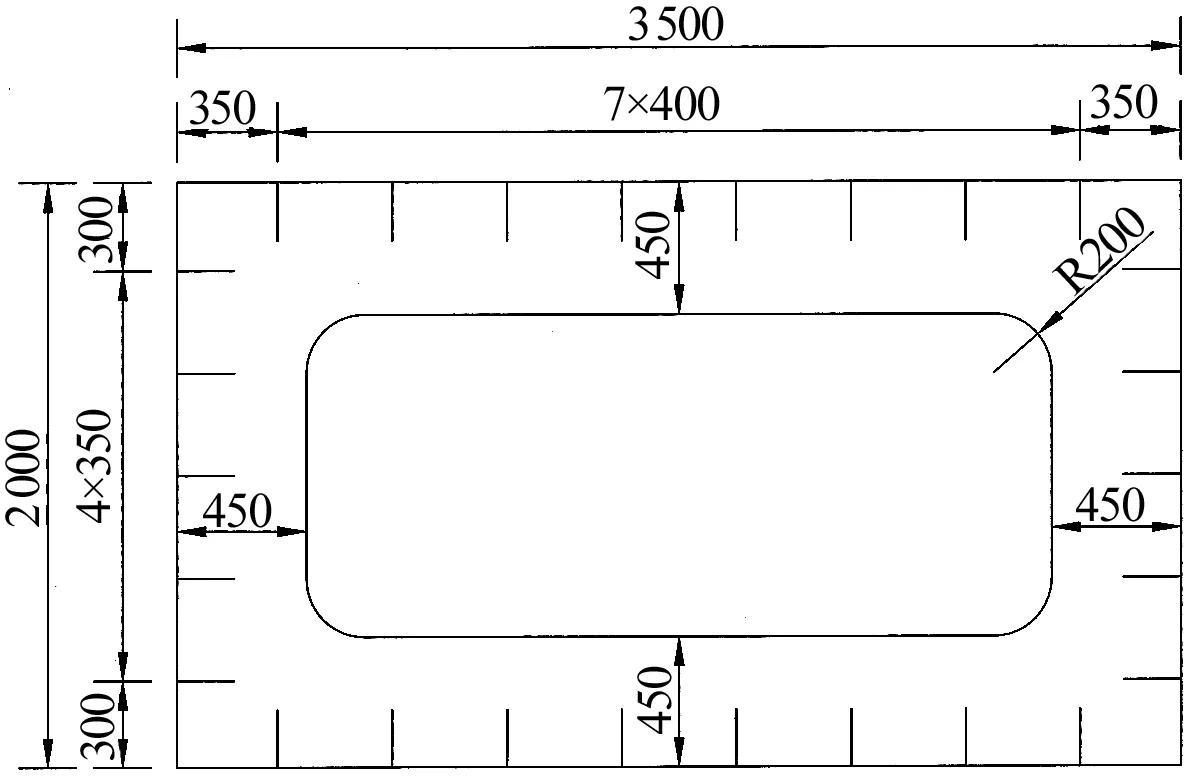
图3 拱脚标准断面(单位:mm)

(a)外侧 (b)内侧图4 拱肋与主梁连接段
2 结构分析计算模型
为分析不同吊杆张拉顺序对拱肋内力的影响,采用有限元软件Midas/Civil 2013建立三维模型,如图5所示。全桥共划分364个节点,383个单元,拱肋、主梁以及拱肋与主梁连接段均采用梁单元模拟,灌注段混凝土采用与拱肋共节点重叠梁单元模拟,吊杆采用只受拉桁架单元模拟。本桥采用支架施工,支架采用只受压弹簧模拟,边界条件均采用一般支承,拱脚完全固结,主梁只有竖向约束。

图5 桥梁有限元模型
3 吊杆张拉方案
本桥为多次超静定结构,按照不同的次序,张拉吊杆相当于给结构施加了不同的荷载,此施工过程中结构的内力是不同的[5],因此需要选择相对安全稳定的张拉顺序。拱桥吊杆张拉施工中,采用对称张拉可以保证结构对称受力,且受力清晰,容易控制。交替张拉,结构内力分布均衡,但张拉设备需往复移动,操作复杂。本文提出6种张拉方案,并进行对比分析[6-7]:
工况Ⅰ,吊杆由拱脚向拱顶依次对称张拉:DS10→DS9……DS2→DS1。
工况Ⅱ,吊杆由拱顶向拱脚依次对称张拉:DS1→DS2……DS9→DS10。
工况Ⅲ,吊杆交替对称张拉:DS4→DS8→DS1→DS6→DS3→DS5→DS9→DS7→DS2→DS10。
常用的吊杆张拉次数有一次张拉法、初张拉和调整张拉的两次张拉法以及多次调整张拉法。一次张拉法可以达到简化张拉工序和缩短工期的目的,但有可能在张拉过程中导致结构某些部位受力不合理。以上3种工况采用一次张拉法,分10个批次,一次张拉力如表1。两次张拉法张拉顺序同一次张拉法,对应的工况名称依次定为Ⅳ、Ⅴ、Ⅵ。初张拉力为表1中设计索力的50%,然后调整张拉至设计索力[8],分20个批次。
表1吊杆设计索力 kN
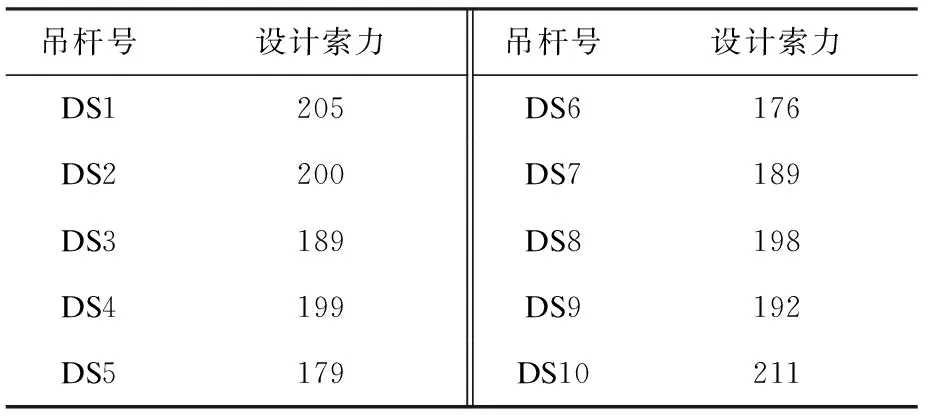
吊杆号设计索力吊杆号设计索力DS1205DS6176DS2200DS7189DS3189DS8198DS4199DS9192DS5179DS10211
4 吊杆张拉过程受力分析
限于文章篇幅以及为方便数据处理,以不同截面命名图表,将不同工况下同一截面的受力置于同一图表中,可直观比较不同工况下主控截面的内力。
4.1一次张拉法
经分析计算,拱肋在一次张拉法Ⅰ、Ⅱ、Ⅲ工况下各主控截面应力值如图6~8所示(图表中应力均为累计应力,受拉为正,受压为负,下同)。
从图6~8中可以看出,拱肋各主控截面上下缘应力线形呈对称性,拱肋受力合理。不同工况下除1/2截面上缘受压下缘受拉外,其他主控截面均是上缘受拉下缘受压。在施工过程中各主控截面应力均在钢材强度设计值之内,故对最终拱肋内力进行比较分析:
第三,信息来源。在保健食品信息寻求方面,有研究指出,标签说明、专业人士(包括医生和营养师),以及亲朋好友被认为是营养和健康信息的可靠来源,虽然广告媒体也是信息传播的主要载体,但是它们也是民众最不信任的来源[28]。当前的研究频频报道健康专业人员的影响力会增加保健食物的消费,这表明卫生专业人员的建议有可能影响老年人的保健食物消费,是可靠和值得信赖的保健食品来源[29]。由于健康信息可以影响消费者对保健食品的接受程度,信息来源的可信度对老年消费者客观理性的理解保健食品并接受它就显得尤为重要。
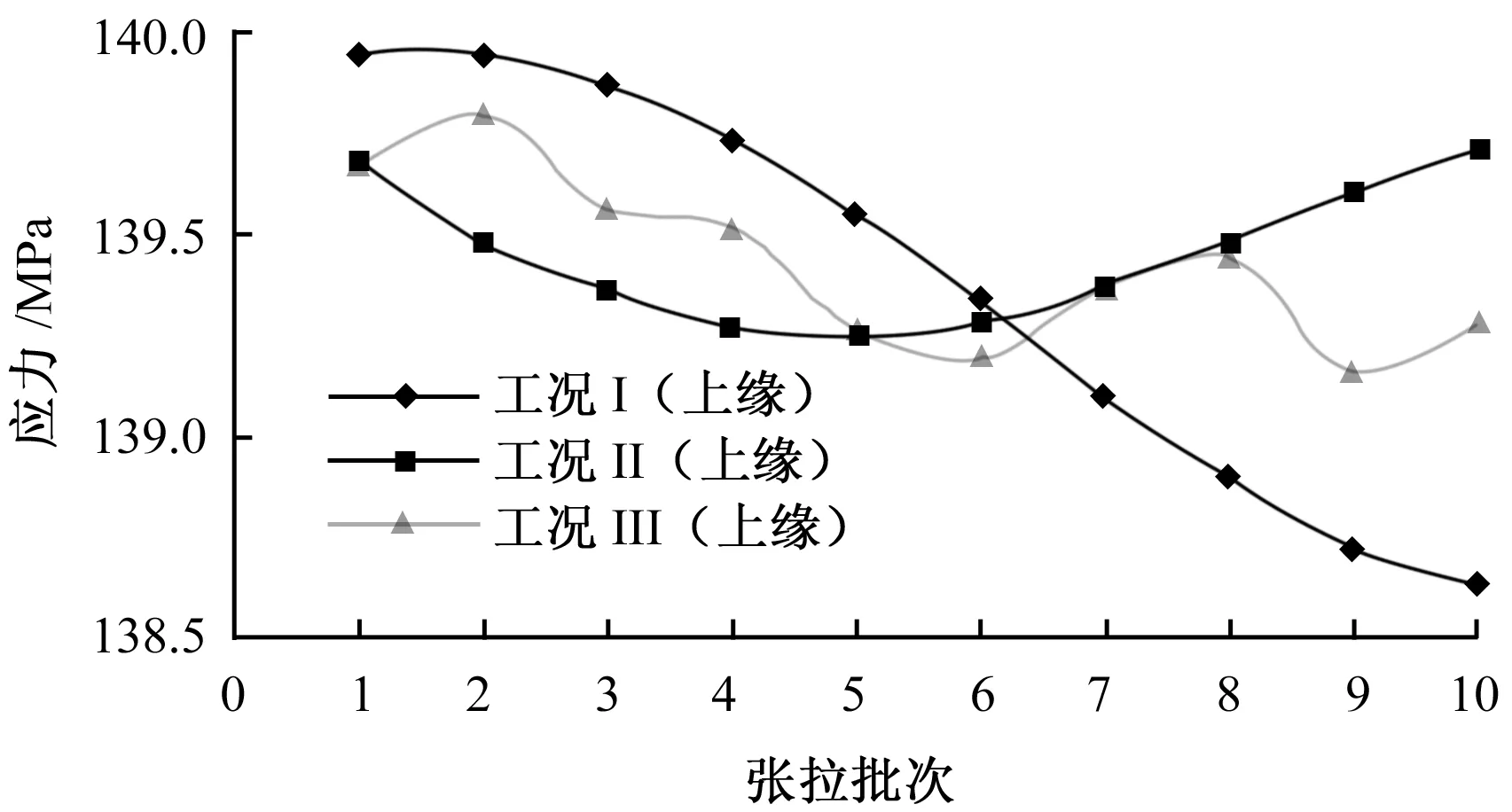
(a)上缘
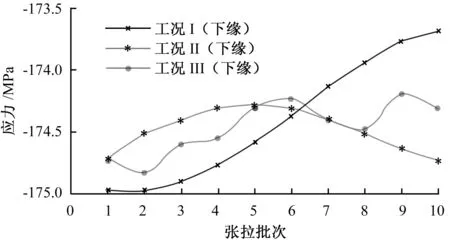
(b)下缘图6 拱脚截面上下缘应力
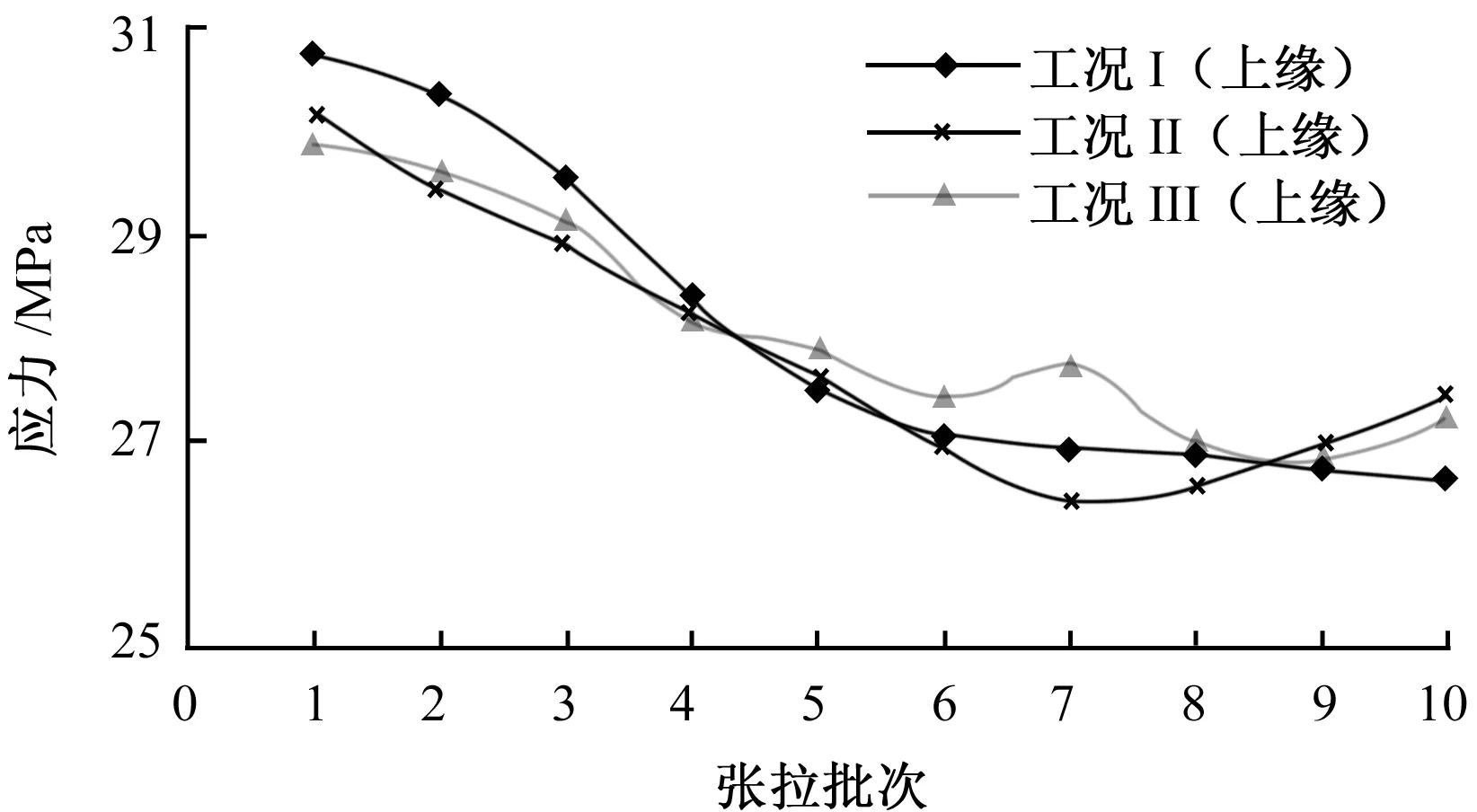
(a)上缘
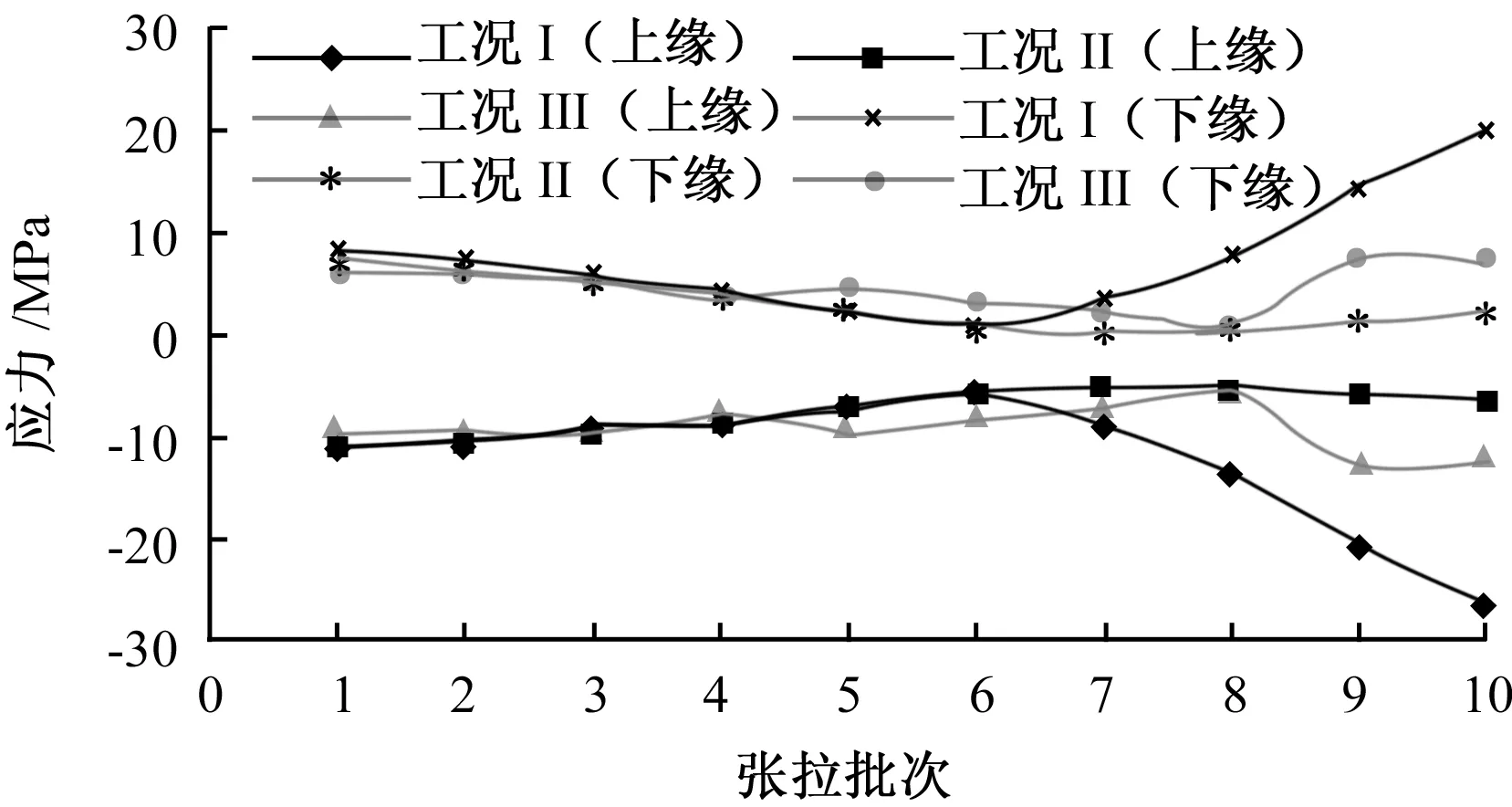
图8 跨中截面上下缘应力
图6中拱脚截面在工况Ⅱ中上(下)缘应力最大,为139.7 MPa(-174.7 MPa);工况Ⅲ中上(下)缘应力次之,为139.3 MPa(-174.3 MPa);工况Ⅰ中上(下)缘应力最小,为138.6 MPa(-173.7 MPa)。
图7(a)中1/4截面上缘应力在工况Ⅱ中最大,工况Ⅲ中次之,工况Ⅰ中最小,依次为27.4 MPa、27.2 MPa、26.6 MPa;图7(b)中1/4截面下缘应力在工况Ⅰ中最大,工况Ⅲ中次之,工况Ⅱ中最小,依次为-33.7 MPa、-33.0 MPa、-32.5 MPa。
图8中1/2截面在工况Ⅰ中上(下)缘应力最大,为-26.5 MPa(19.9 MPa);工况Ⅲ中上(下)缘应力次之,为-12.2 MPa(7.0 MPa);工况Ⅱ中上(下)缘应力最小,为-6.4 MPa(2.1 MPa)。
综上比较,工况Ⅰ中拱脚截面应力最小,1/2截面应力大;工况Ⅱ中1/2截面应力最小,拱脚截面应力最大;工况Ⅲ中各截面应力居中。故,按工况Ⅲ顺序张拉吊杆可使拱肋受力较为均匀,方案较为合理。
4.2两次张拉法
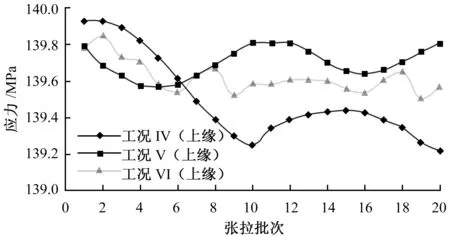
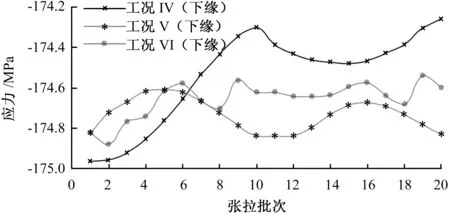
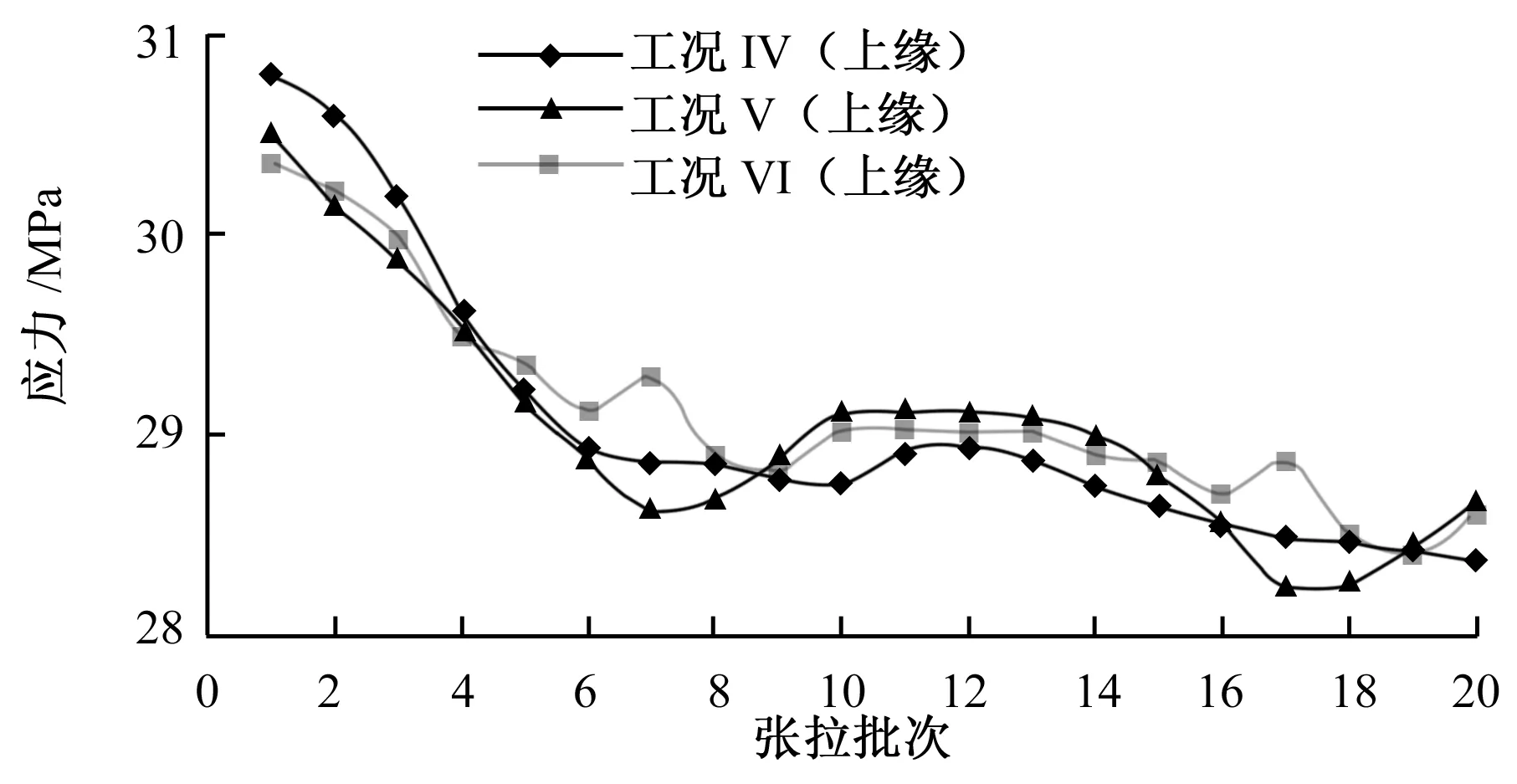
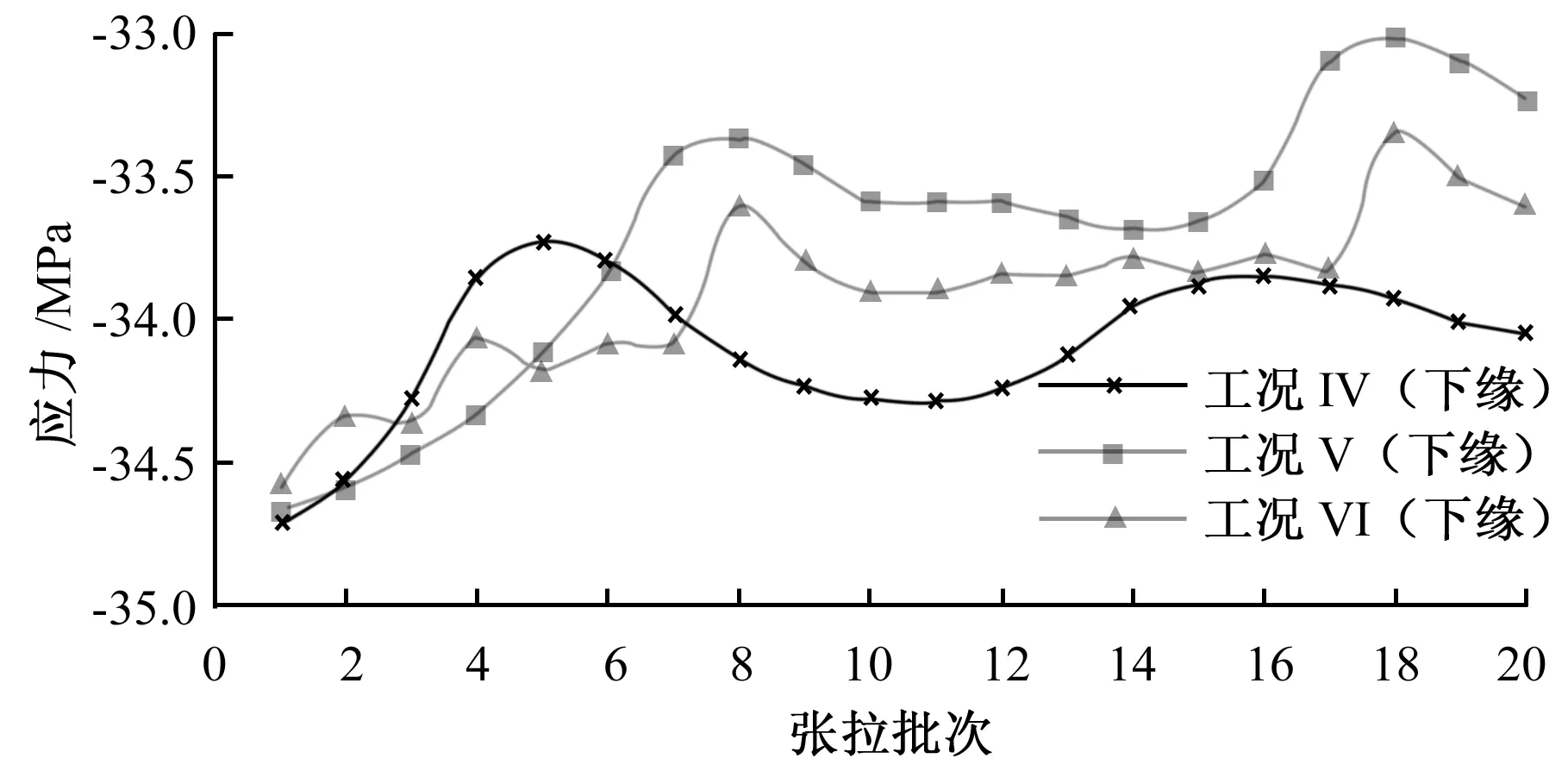
拱肋在两次张拉法Ⅳ、Ⅴ、Ⅵ工况下拱肋主控截面应力值如图9~11所示。
(a)上缘
(b)下缘图9 拱脚截面上下缘应力
(a)上缘
(b)下缘图10 1/4截面上下缘应力
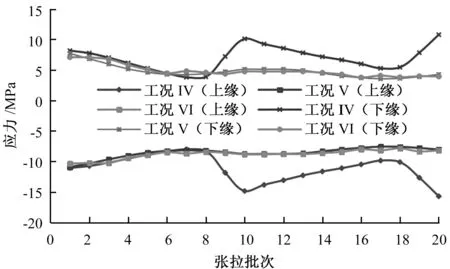
图11 跨中截面上下缘应力
由图9~11可见,拱肋各主控截面均未超过钢材强度设计值,初张拉时各主控截面内力除应力值不同,走势与一次张拉法截面应力走势一致。调整张拉阶段拱脚截面应力有小幅波动,但最终仍呈减小趋势。调整张拉完成后,各截面上下缘受力类型与一次张拉法下受力类型相同。
图9中拱脚截面在工况Ⅴ中上(下)缘应力最大,为139.8 MPa(-174.8 MPa);工况Ⅵ中上(下)缘应力次之,为139.5 MPa(-174.6 MPa);工况Ⅳ中上(下)缘应力最小,为139.2 MPa(-174.3 MPa)。
图10(a)中1/4截面上缘应力在工况Ⅴ中最大,工况Ⅵ中次之,工况Ⅳ中最小,依次为28.65 MPa、28.6 MPa、28.37 MPa;图10(b)中1/4截面下缘应力在工况Ⅳ中最大,工况Ⅵ中次之,工况Ⅴ中最小,依次为-34.05 MPa、-33.6 MPa、-32.2 MPa。
综上比较,与一次张拉法结果一致,工况Ⅵ中拱脚截面应力最小,1/2截面应力大;工况Ⅴ中1/2截面应力最小,拱脚截面应力最大;工况Ⅵ中各截面应力居中。故,工况Ⅵ张拉方案用于施工是较为合理的。
5 Ⅲ、Ⅵ吊杆张拉方案比较
由以上分析得工况Ⅲ和Ⅵ的张拉顺序分别为一次张拉法和两次张拉法中较为优越的张拉方案。现以内力与位移为分析对象,进一步比较两方案的优越性。
5.1工况Ⅲ、Ⅵ截面应力
表2中列出Ⅲ和Ⅵ两工况下拱肋各主控截面的应力,以对比工况Ⅲ与工况Ⅵ的优劣。
表2Ⅲ、Ⅵ工况主控截面应力 MPa

工况支点1/4截面跨中截面ⅢⅥ上缘139.327.2-12.2下缘-174.3-33.07.0上缘139.528.6-8.2下缘-174.6-33.63.95
由表2可知,Ⅲ工况下支点截面上(下)缘应力为139.3 MPa(-174.3 MPa),与Ⅵ工况下拱肋支点截面上下缘应力差值为-0.2 MPa(0.3 MPa),Ⅲ、Ⅵ工况中1/4截面上下缘应力差值为-1.4 MPa(0.6 MPa),1/2截面上下缘应力差值为4.0 MPa(-3.05 MPa)。由此可见,工况Ⅵ下支点截面与1/4截面最终应力较工况Ⅲ稍大,跨中截面应力较小,综上再考虑施工安全稳定及施工方便性与经济性,选用一次张拉法的工况Ⅲ更为合理。
5.2拱肋与吊杆连接处节点位移分析
桥梁线形控制是确保桥梁施工宏观质量控制的主控及桥梁建设的安全保证[9],表3列出工况Ⅲ与工况Ⅵ下拱肋与吊杆连接处的节点位移。
表3吊杆与拱肋连接处节点位移值 mm
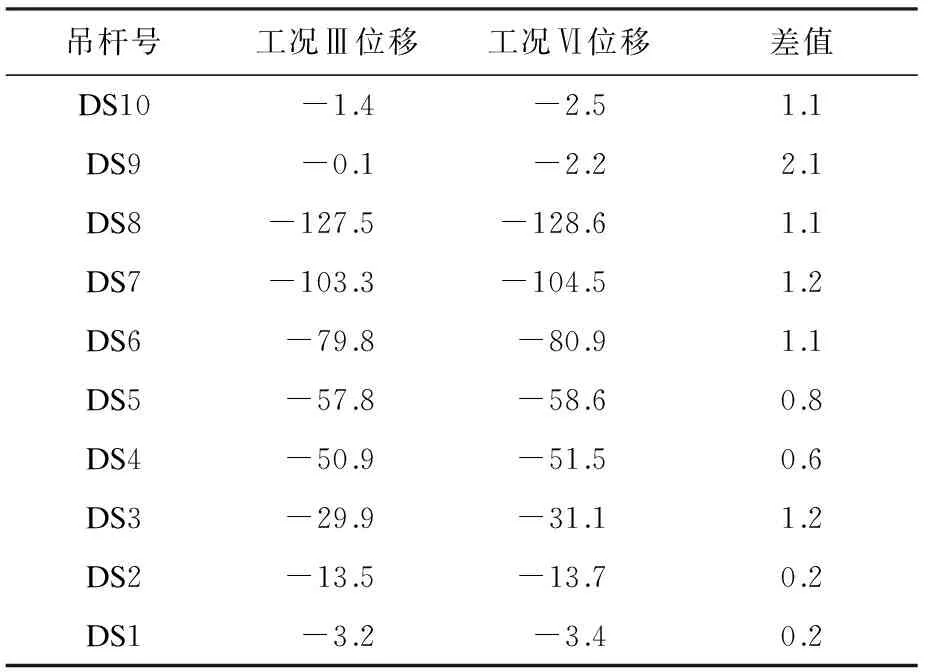
吊杆号工况Ⅲ位移工况Ⅵ位移差值DS10-1.4-2.51.1DS9-0.1-2.22.1DS8-127.5-128.61.1DS7-103.3-104.51.2DS6-79.8-80.91.1DS5-57.8-58.60.8DS4-50.9-51.50.6DS3-29.9-31.11.2DS2-13.5-13.70.2DS1-3.2-3.40.2
由表3可以看出,不同工况下拱脚吊杆附近与跨中附近位移较小,其他位置位移较大;对比Ⅲ、Ⅵ工况下拱肋吊杆节点处位移可知,Ⅵ工况下位移较Ⅲ工况下位移较小,且DS1处位移差值最小,为0.2 mm,DS9处位移差值最大,为2.1 mm。可见,工况Ⅵ下拱肋位移比工况Ⅲ下拱肋位移大,因此,按工况Ⅲ顺序张拉吊杆更为合理。
6 结论
本文针对某异形钢拱桥吊杆张拉施工提出了6种吊杆张拉方案,采用Midas/Civil 2013软件建模进行仿真计算,对不同张拉方案下拱肋内力变化及最终变形进行了分析,得出:
1)对本类轻型钢拱桥而言,不同吊杆张拉顺序会对结构受力产生一定的影响,但不会引起结构产生过大的局部应力。
2)两次张拉法张拉吊杆过程中调整张拉对结构内力的影响与初张拉的影响基本一致,交替对称张拉可使拱肋受力更为均衡,两次张拉与一次张拉对结构的最终应力影响相差较小。
3)在施工过程中没有出现局部应力超过材料强度设计值,选用最终结构内力及变形较小的施工方案:交替对称一次张拉至最终索力的工况Ⅲ张拉顺序。
[1]金立新,潘盛山,郭慧乾,等.国内外对角斜跨拱桥的设计与施工[J].公路,2011(9):74-78.
[2]张俊平,刘爱荣,李永河.蝴蝶拱桥的模型试验与理论研究[J].桥梁建设,2007(2):15-17.
[3]李新平,颜显玉,陈孔亮.外倾式组合拱桥吊杆张拉力的确定及分析[J].科学技术与工程,2009(1):311-315.
[4]单成林.拱桥吊杆的更换设计及施工方法[J].中外公路,2009(8):151-153.
[5]苏庆田,李伟,张立鹏,等.外倾式拱桥吊杆及临时支架施工顺序优化[J].结构工程师,2013(3):139-144.
[7]黄伟,杨磊,丁琼迪.空间扭转系杆拱桥吊杆张拉顺序优化[J].安徽工业大学学报(自然科学版),2012(4):361-364.
[8]张连海,刘凡,李新生,等.系杆拱桥半刚性吊杆初始张拉力分析与测定[J].苏州科技学院学报(工程技术版),2011(1):37-40.
[9]赵伟,郑剑涵,陆森强.特大跨系杆钢拱桥成桥状态与吊杆张拉力优化分析[J].中外公路,2016(1):113-118.
责任编辑:唐海燕
Influence of Sequences of Suspender Tensions Upon Inner Force of Arch Rib of Steel Arch Bridge with Single Extraversive Rib
A finite element model was established by using Midas/Civil to study special-shaped steel arch bridge with single extraversive rib and to analyze the influence of tension order and number of tensions upon the inner force and displacement of the hoisting point.Considering internal force balance,safety,convenience and economy,a reasonable tensioning scheme was proposed that suspenders be tensioned alternately and symmetrically to final tensile force in one time.
single extraversive rib;steel arch bridge;hanger;tension sequence;finite element analysis
10.3969/j.issn.1671-0436.2016.04.002
2016- 03-14
汪一意(1992—),男,硕士研究生。
U442.5;U448.22
A
1671- 0436(2016)04- 0007- 05
