基于组合测距的无线传感器网络自定位算法*

郄剑文，贾方秀，李兴隆，王晓鸣

（1.南京理工大学智能弹药技术国防重点学科实验室，南京210094；2.中国工程物理研究院化工材料研究所，四川绵阳621900）

基于组合测距的无线传感器网络自定位算法*

郄剑文1*，贾方秀1，李兴隆2，王晓鸣1

（1.南京理工大学智能弹药技术国防重点学科实验室，南京210094；2.中国工程物理研究院化工材料研究所，四川绵阳621900）

针对如何在锚节点密度较低的情况下提高无线传感器网络中节点自定位精度的问题，本文提出了一种基于RSSI和TDOA组合测距的加权质心定位算法。该算法分别对传统RSSI和TDOA测距模型增加了校验参数及温度补偿，将未知节点与锚节点间距离估计值的倒数作为权值参数，再利用加权质心算法计算出未知节点的位置坐标。硬件试验表明室内环境中基于改进RSSI测距模型的定位算法相比于传统RSSI质心定位算法的误差改进比率为56.2%，仿真结果显示基于组合测距的定位算法在锚节点密度较低时也能达到较高的定位精度。

无线传感器网络；定位；信号强度指示；到达时间差

EEACC：7230；6150Pdoi：10.3969/j.issn.1004-1699.2016.05.020

无线传感器网络［1-3］WSN（Wireless Sensor Net⁃works）的定位是指自组织的网络通过特定的方法提供节点位置信息，一般分为节点自身定位和目标定位。在定位技术相关研究中，根据是否已知自身的位置，将传感器节点分为锚节点（Beacon node）和未知节点（Unknown node）。按照定位过程中是否测量节点间的距离，定位算法分为基于距离（Range-based）和距离无关（Rage-free）的定位算法［4］。

Range-based定位算法主要有三边测量法、三角测量法等［5-6］。其中较常用的测距技术有信号强度指示RSSI（received signal strength indication）到达时间差TDOA（time difference of arrival）和到达时间TOA（time of arrive）等［7-9］。常见的Rage-free定位算法有质心算法、距离向量-跳段算法DV-HOP（distance vector-hop）和Amorphous算法等［10-11］。文献［12］研究表明，RSSI是一种低功率、低成本的测距技术，但测距精度较低，可能产生±50%的测距误差。文献［13］提出了一种基于超声波信号的TDOA定位方法，该方法同时使用扩展卡尔曼滤波和鲁棒扩展卡尔曼滤波去除环境噪声，其定位误差在室内视距环境下可达到0.3 m，但其仅能实现小范围的高精度定位。为解决Range-based定位系统硬件功耗较高的问题，Belusu和Heidemann等人率先提出了低功耗的质心定位算法［14］，该算法利用质心公式将节点间跳数与节点位置之间建立联系，适用于环境多变条件下大规模WSN网络定位，但其定位精度较低。

基于上述研究，本文在改进传统测距模型的基础上，提出一种基于RSSI和TDOA组合测距的无线传感器网络加权质心定位算法。将RSSI测距范围广和TDOA测距精度高的优势相结合，以求在网络中锚节点密度较低的情况下达到较高的节点自定位精度，并进行了硬件试验与软件仿真验证该定位算法的定位精度。

1　RSSI测距算法

1.1传统RSSI测距模型

WSN研究中常用的无线信号传播路径损耗模型有Free-space模型［15］和Shadowing模型［16］。经典Free-space模型为

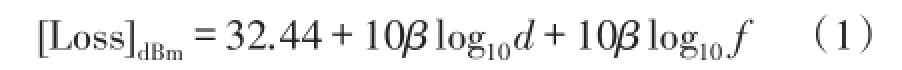
其中d为接收对象与信源间的距离，单位为km；f为信号的频率，单位为MHz；β为路径衰减系数，其典型值见表1。该模型只适用于信号短距离传播损耗的计算。

表1　β的几种典型值

在WSN实际应用中，Shadowing模型是一个被广泛应用的模型，以dB作为计量单位的对数正太Shadowing模型为

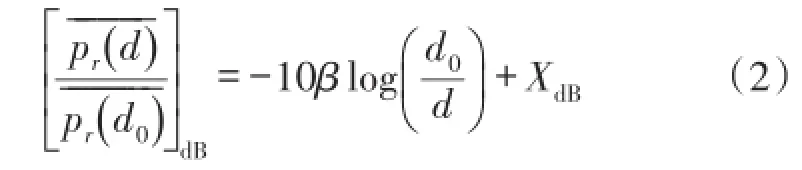
dB一个高斯随机变量。该模型中通常取基准距离d0为1 m。本文将采用Shadowing简化模型，即将模型中的第2部分进行忽略。

1.2改进测距模型

在实际应用中，由于多径、绕射、障碍物等因素的影响，相对位置固定的同一节点对在不同环境下的RSSI值相差很大。此外，距离一定的节点对在同一环境下的不同区域或者不同方位条件下，RSSI值也不一定相同。所以在同一网络拓扑结构中，相同的RSSI值对于不同的节点对代表着不同的距离。本文将锚节点之间的距离参数和信号强度两种信息作为参考来校正未知节点与锚节点间的距离估计值，以提高测距算法的精度和环境适应性。

如图1所示，假设N是未知节点，锚节点对Mi和Mj之间的距离记为Dij。在一定时间内，记N收到固定锚节点Mi信号的RSSI平均值为RSSIi，信号强度平均值为Pi；锚节点Mi收到锚节点Mj信号的RSSI平均值为RSSIij，信号强度平均值为Pij。则有关系式

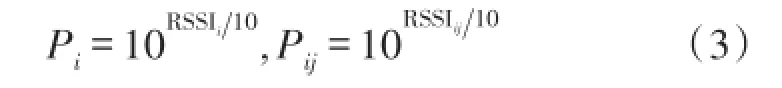
式中RSSI平均值RSSIi和RSSIij单位为dBm；信号强度平均值Pi和Pij单位为mW。

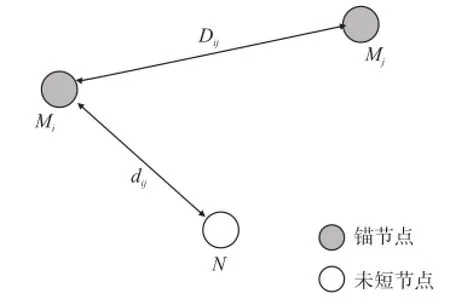
图1　测距校正模型

图1中dij表示以锚节点对Mi和Mj的相关信息作为参考，利用简化Shadowing模型计算得到的未知节点N与锚节点Mi之间的距离值，即

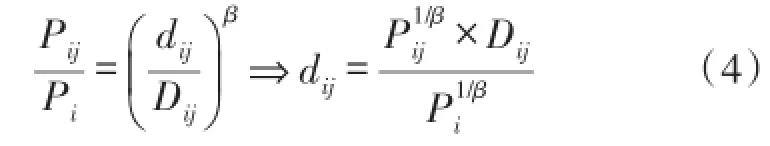
将锚节点Mi能探测到的锚节点个数记为m，则将未知节点N到锚节点Mi的校正距离di表示为以Mi和Mj（1≤j≤m）间距离及信号强度为参考计算得到的估计距离dij的平均值，即

2　TDOA测距算法

2.1基于温度补偿的超声波测距模型

超声波是一种频率超过2 kHz的弹性机械波，超声波精确测距在各个领域中已经得到了广泛的应用，其精度在一定测距范围内能达到厘米级别［17］。由于温度的变化对超声波传播速度的影响最大，所以本文建立基于温度补偿的超声波测距模型。

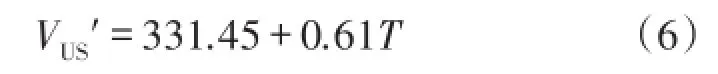
式中VUS′为加温度补偿后的声速，单位为m/s；T为环境实际的温度，单位为℃。

2.2TDOA测距模型

针对TDOA测距模型，本文选用无线射频信号和超声波信号。如图2所示，在同一传播介质中，假设VRF、VUS分别为无线射频信号与超声波信号的传播速度，则其到达同一节点的时间差Δt为

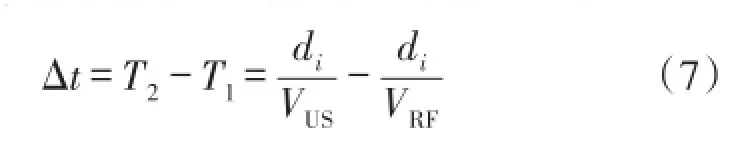
求解di得

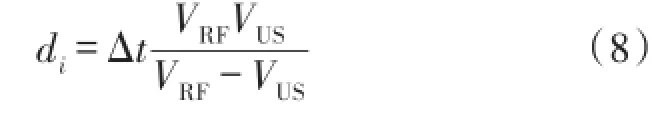
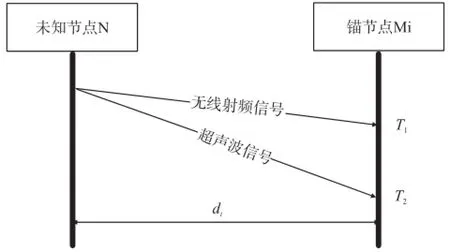
图2　TDOA测距示意图

常温常压下，超声波在空气中的传播速度VUS≈344 m/s，无线射频信号的传播速度可以达到VRF≈3× 108m/s，即VRF远大于VUS，所以距离的计算公式可以简化为

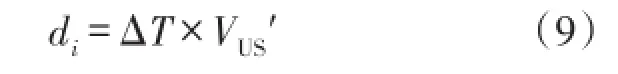
3　组合定位算法设计

3.1组合测距

由于TDOA测距算法需要同时获得射频信号和超声波信号，且超声波信号的有效作用距离仅为5 m左右。这导致基于此测距方法的定位算法对网络中锚节点的分布密度要求很高，虽然能够达到较高的定位精度，但定位成功率较低；RSSI测距中射频信号的传输距离远比超声波传播距离远，但由于实际环境中的干扰、遮挡、反射等因素的影响，测得的信号强度损耗和理论值有一定差距，测距算法精度相对较低。

综合考虑以上两种测距算法的优缺点，本文提出了基于TDOA和RSSI校验的组合测距算法。通过TDOA测距算法提高总体的测距精度，而其作用范围小的缺陷由RSSI测距算法进行弥补。组合测距算法优先选择TDOA测距，在其作用范围之外采用RSSI测距。

3.2加权质心定位算法

加权质心定位算法［18-19］主要是利用未知节点与锚节点之间的信号强度值来计算各个锚节点的权值。如图3所示，设WSN中n个锚节点Mi的位置坐标为（Xi，Yi）。未知节点N的估测坐标为（Xe，Ye），则加权质心算法计算公式为

式中Wi表示各个锚节点在定位算法中的权值参数，若未知节点N无法与锚节点Mi通信，则Wi的值为0。

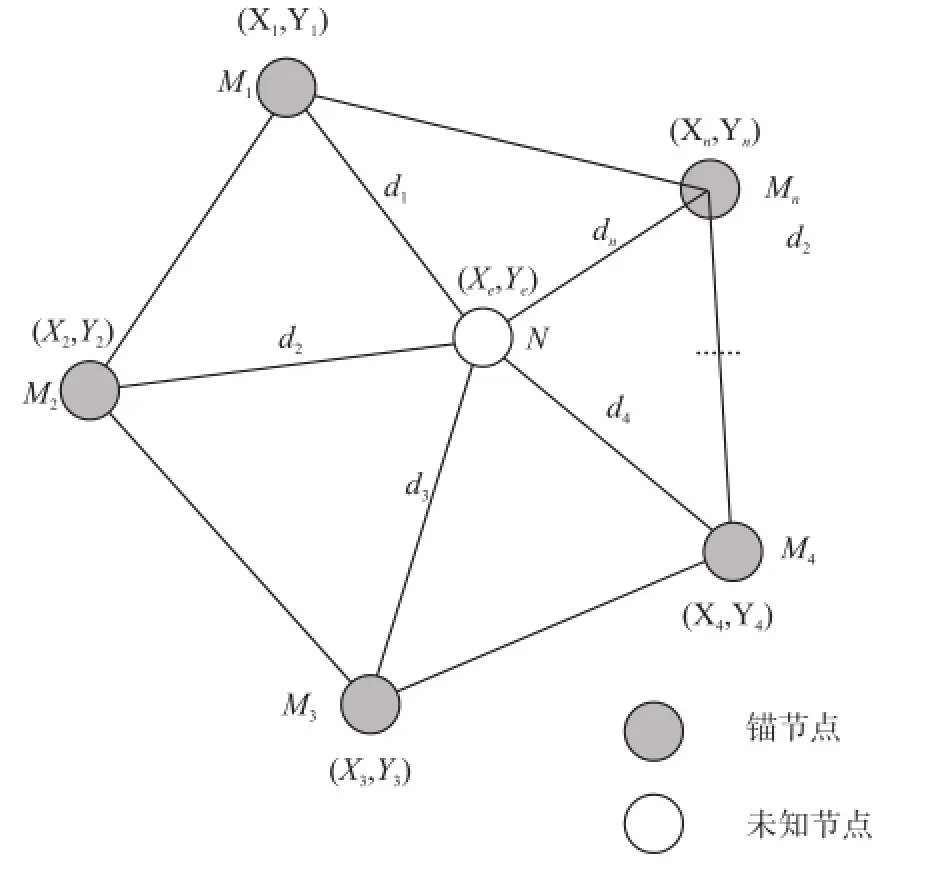
图3　质心定位算法示意图

综合考虑组合测距算法的精度以及权值参数的合理性，本文选取未知节点与锚节点间估计距离di的倒数作为该锚节点的定位权值Wi，即

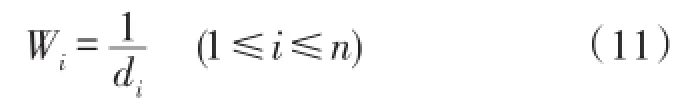
此权值参数的选取体现出了距离未知节点近的锚节点权值较大，这是因为距离越近测距误差相对越小。显然该权值参数的选取方法能够合理得体现出各个锚节点对于未知节点估计位置的决定权大小。设未知节点的真实位置坐标为（xe，ye）。则定义算法的绝对定位误差ER为

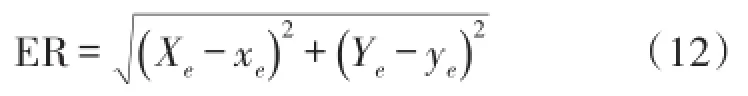
3.3定位算法流程设计

本文提出的定位算法是基于WSN已完成自组网并形成稳定节点簇前提下的。如图4所示，在传感器网络自组网完成之后，锚节点对之间收发RF信号，以获取当前环境中的RSSI校验参数。同时未知节点广播自身ID并周期性的发出RF及US信号，若锚节点返回TDOA测距结果，则优先采用此数值。若未返回TDOA测距结果，则针对此锚节点采用RSSI校验测距。遍历簇中所有锚节点，对未知节点采用上述加权质心定位算法，以计算结果更新节点位置信息表。

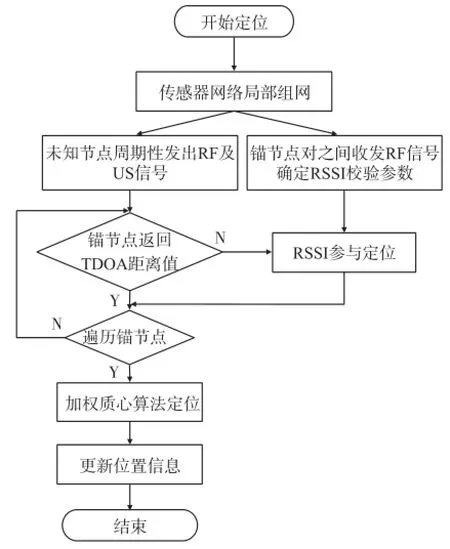
图4　定位算法流程图

4　模拟试验及仿真

4.1硬件模拟试验

由于实际硬件数量与场地的限制，现分别对单个定位算法进行小范围定位试验，以评估基于RSSI改进模型及TDOA补偿模型的定位算法性能。针对本文具体的硬件实现，将d=1 m，f=2.4 GHz，β=1.7代入式（1）中可计算出）的值。如图1所示，将5个无线传感器节点直接摆放到地面上，其中4个节点分别摆放到3 m×4 m矩形试验区域的四个顶点处，作为网络中的锚节点。则锚节点的位置坐标分别为M（10，0），M（23，0），M（33，4），M（40，4），未知节点将接收到的RSSI数据无线传输给协调器，协调器通过串口与上位机相连。试验区域中每个小方格为0.5 m× 0.5 m，显然整个试验区域内有35个交叉格点，且均在超声波测距范围内。则随机选取12个交叉格点作为未知节点的位置，分别使用基于传统RSSI测距模型、改进RSSI测距模型和TDOA温度补偿测距模型的三种加权质心定位算法进行定位计算。

算法试验分为两个阶段，第一阶段是RSSI和TDOA原始数据采集阶段，周期性的采集未知节点接收到锚节点的RSSI和TDOA数据及锚节点之间的RSSI数据，并将数据存储到上位机中。第二阶段就是利用本文中的定位算法对未知节点进行定位计算。

图5　硬件试验

对于RSSI改进定位算法，由于试验是在室内环境中进行的，由表1可知，β取值范围为1.6～1.8，则在此范围内分析试验数据可得表2。从中可知，RSSI改进定位算法在β=1.7时定位试验平均误差及方差最小，则取β=1.7时该算法的定位结果与其他两种定位算法进行比较。

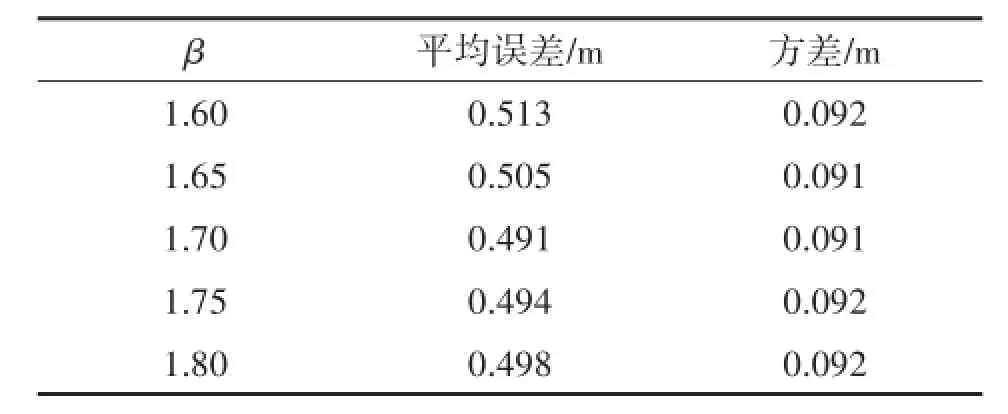
表2　不同β值RSSI改进定位算法结果

3种定位算法硬件试验结果如图6所示，由拟合曲线可以看出RSSI改进算法的定位精度及误差稳定性明显高于传统RSSI质心定位算法，由具体的试验数据计算可得其平均误差改进比率为56.2%，标准偏差改进比率为49.5%。而TDOA定位算法的平均误差及标准偏差最小，这也体现出了其在小范围定位中的优势。

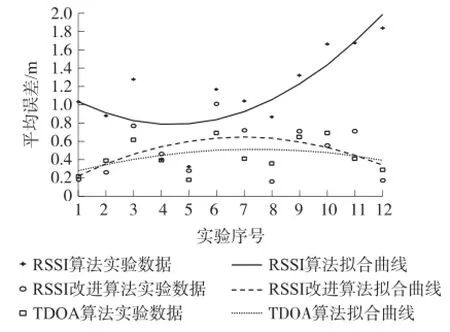
图6　硬件试验结果（β=1.7）

4.2算法软件仿真

为全面评估本文所提出的基于RSSI和TDOA组合测距定位算法的性能，本文采用C++平台对此进行仿真分析。仿真试验的初始条件为：100个WSN节点随机分布在100 m×100 m的区域内，节点通讯半径设为20 m，超声波有效测距范围设为5 m，锚节点密度的变化范围为20%～40%。本文在仿真试验环境参数中加入满足正态分布的随机噪声，来模拟真实环境中反射、折射及多径现象对无线信号的影响。结合硬件试验数据，取TDOA测距的绝对测距误差满足NT（0.537，1.0432），改进RSSI测距模型的绝对测距误差满足NM（2.379，2.0762），传统RSSI测距的绝对测距误差满足NR（10.288，3.5582）。在不同锚节点密度的条件下，分别仿真500次，仿真结果取500次模拟试验的平均值，如图7所示。

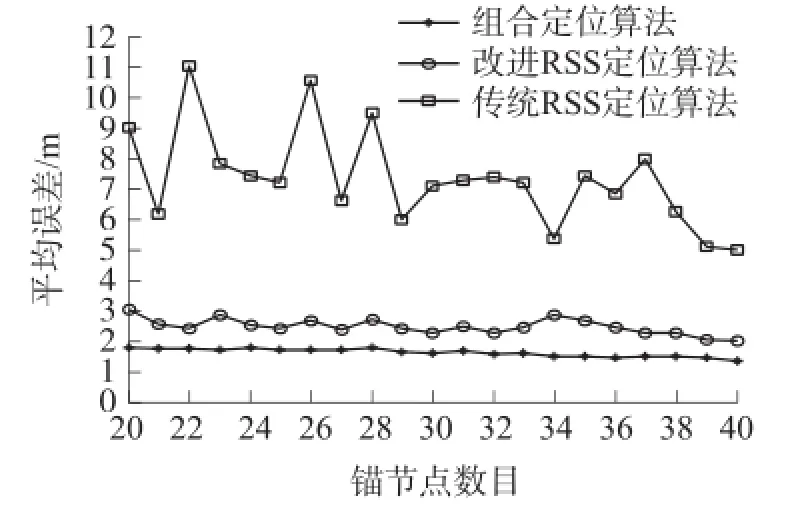
图7　软件仿真结果

软件仿真结果表明，相比于另外两种定位算法，基于组合测距的定位算法在不同的锚节点密度下均有较高的定位精度及稳定性。相比于传统RSSI定位算法的平均误差改进比率为77.9%，相比于改进的RSSI定位算法的平均误差改进比率为34.4%。且锚节点密度在低于30%的情况下，组合算法的定位精度也能达到2 m以内。

5　结论

针对低锚节点密度条件下如何提高无线传感器网络节点自定位精度的问题，本文将RSSI测距算法覆盖范围广和TDOA测距算法精度高的优势相结合，分别对传统RSSI和TDOA测距模型增加了校验参数及温度补偿，在此基础上提出一种基于RSSI和TDOA组合测距的无线传感器网络加权质心定位算法。硬件试验及软件仿真结果表明，该定位算法相比于传统RSSI定位算法的平均误差改进比率为77.9%，标准偏差改进比率为81.5%。在锚节点密度低于30%的情况下，组合算法的定位精度也能达到2 m以内。

［1］Chaturvedi P，Daniel A K.Wireless Sensor Networks—A Survey［J］.Int Conf on Recent Trends in Information Telecommunication and Computing Itc，2014，38（6）：393-422.

［2］Yao L I，Hua N，Tian L G，et al.A Survey on Cluster Based Rout⁃ing Protocols in Wireless Sensor Networks［J］.Telecommunica⁃tion Engineering，2015，45（18）：687-695.

［3］Rawat P，Singh K D，Chaouchi H，et al.Wireless Sensor Net⁃works：a Survey on Recent Developments and Potential Synergies［J］.Journal of Supercomputing，2014，68（1）：1-48.

［4］Han G，Xu H，Duong T Q，et al.Localization Algorithms of Wire⁃less Sensor Networks：a Survey［J］.Telecommunication Systems，2013，52（4）：2419-2436.

［5］Lee J K，Kim Y，Lee J H，et al.An Efficient Three-Dimensional Localization Scheme Using Trilateration in Wireless Sensor Net⁃works［J］.IEEE Communications Letters，2014，18（9）：1591-1594.

［6］Misra R，Shukla S，Chandel V.Lightweight Localization Using Tri⁃lateration for Sensor Networks［J］.International Journal ofWire⁃less Information Networks，2014，21（2）：89-100.

［7］姜志鹏，陈正宇，刘影，等.TOA定位算法非线性优化问题研究［J］.传感技术学报，2015，28（11）：1716-1719.

［8］张会新，陈德沅，彭晴晴，等.一种改进的TDOA无线传感器网络节点定位算法［J］.传感技术学报，2015，28（3）：412-415.

［9］Liu C，Yang J，Wang F.Joint TDOA and AOA location algorithm［J］.Journal of Systems Engineering and Electronics，2013，24（2）：183-188.

［10］Maung N A M，Kawai M.Experimental Evaluations of RSS Threshold-Based Optimised DV-HOP Localisation For Wireless Ad-Hoc Networks［J］.Electronics Letters，2014，50（17）：1246-1248.

［11］Zhao L Z，Wen X B，Li D.Amorphous Localization Algorithm Based on BP Artificial Neural Network［J］.International Journal of Distributed Sensor Networks，2015，2015.

［12］Meguerdichian S，Slijepcevic S，Karayan V，et al.Localized Algorithms in Wireless Ad-Hoc Networks：Location Discovery and Sensor Exposure［J］.Proceedings of Mobihoc，2001：106-116.

［13］Zhang R，Hoflinger F，Reindl L.TDOA-Based Localization Using Interacting Multiple Model Estimator and Ultrasonic Transmitter/ Receiver［J］.IEEE Transactions on Instrumentation and Measure⁃ment，2013，62（8）：2205-2214.

［14］Bulusu N，Heidemann J，Estrin D.GPS-Less Low Cost Outdoor Optimization For Very Small Devices［J］.IEEE Personal Commu⁃nications Magazine，2000，7（5）：28-34.

［15］Zhao J，Li H，Sun X.Research on the Signal Random Attenuation Coefficient Based on RSSI in WSN Localization Technology［C］// Wireless Communications，Networking and Mobile Computing，2009.WiCom'09.5th International Conference on.IEEE，2009：1-4.

［16］Mao G，Anderson B D O，Fidan B.Path Loss Exponent Estimation For Wireless Sensor Network Localization［J］.Computer Net⁃works，2007，51（10）：2467-2483.

［17］Can Basaran，Jong Wan Yoon，Sang Hyuk Son，Taejoon Park.Self-Configuring Indoor Localization Based on Low-Cost UltrasonicRange Sensors［J］.Sensors，2014，14（10）：18728-18747.

［18］Zhao C，Xu Y，Huang H.Weighted Centroid Localization Based on Compressive Sensing［J］.Wireless Networks，2014，20（6）：1527-1540.

［19］Wang J，Urriza P，Han Y，et al.Weighted Centroid Localization Algorithm：Theoretical Analysis and Distributed Implementati-on.［J］.IEEE Transactions on Wireless Co-mmunications，2011，10（10）：3403-3413.

郄剑文（1992-），男，汉族，内蒙古包头人，南京理工大学机械工程学院机械电子工程专业硕士研究生，主要为研究方向为无线传感器网络技术，qiejian⁃wen55@163.com；

贾方秀（1980-），女，博士，南京理工大学机械工程学院讲师，主要为研究方向为MEMS惯性传感器电路设计及IMU姿态测量技术，jiafangxiu@gmail，com；

王晓鸣（1962-），男，汉族，南京理工大学机械工程学院教授，博士生导师。中国兵工学会理事，中国兵工学会弹药专业委员会主任委员，主要为研究方向为弹药精确化与智能化技术，202xm@163.com。

Self-Localization Algorithm Based on Integrated Ranging in Wireless Sensor Networks*

QIE Jianwen1*，JIA Fangxiu1，LI Xinglong2，WANG Xiaoming1
（1.Ministerial Key Laboratory of Intelligent Ammunition，Nanjing University of Science and Technology，Nanjing 210094，China；2.Institute of Chemical Materials of CAEP，Mianyang Sichuan 621900，China）

In order to improve the self-localization accuracy at a low beacon node density in Wireless Sensor Net⁃works（WSN）.A weighted centroid localization algorithm based on received signal strength indication（RSSI）and time difference of arrival（TDOA）is proposed.The algorithm adds calibration parameters and temperature compensa⁃tion for RSSI and TDOA ranging model.The inverse of the estimate distance between the unknown node and beacon node is used as the weight parameter.Then the position coordinates of unknown nodes are calculated by the weight⁃ed centroid algorithm.The hardware test and software simulation results show that the error improvement rate of pro⁃posed algorithm is more than 50%and it can achieve a relatively high localization accuracy under the condition of low beacon node density.

wireless sensor networks；location；received signal strength indication；time difference of arrive

TP301.6

A

1004-1699（2016）05-0739-06

项目来源：国家自然科学基金项目（61201391）

2015-12-29修改日期：2016-01-20