永磁同步电机的无差拍预测转矩控制系统*
2016-10-26浦龙梅张宏立
浦龙梅, 张宏立
(1. 新疆建设职业技术学院,新疆 乌鲁木齐 830000;2. 新疆大学 电气工程学院,新疆 乌鲁木齐 830000)
永磁同步电机的无差拍预测转矩控制系统*
浦龙梅1,张宏立2
(1. 新疆建设职业技术学院,新疆 乌鲁木齐830000;2. 新疆大学 电气工程学院,新疆 乌鲁木齐830000)
将无差拍控制理论应用于永磁同步电机预测转矩控制系统,通过求解无差拍期望电压矢量,判断其空间位置,缩小逆变器输出电压矢量的优选范围。应用无差拍预测转矩控制策略,单步预测滚动优化次数由传统预测转矩控制的7次降低至3次,多步预测节省系统运算资源的效果更优。仿真和试验结果表明无差拍预测转矩控制策略在继承预测转矩控制优越动、稳态性能的同时还能减轻系统的运算负担。
无差拍控制; 预测转矩控制; 运算负担; 滚动优化
0 引 言
有限控制集模型预测控制(Finite Control Set Model Predictive Control, FCS-MPC)自提出以来[1],得到了诸多学者的广泛关注。预测转矩控制(Predictive Torque Control, PTC)在保持传统直接转矩控制高动态性能的同时,在处理非线性约束问题时具有更优的灵活性[2]。但是,转矩预测在线寻优算法运算量巨大[3],尤其应用于多步预测控制或者多电平、不对称拓扑结构时,对控制系统硬件支撑提出了一定的挑战。在同一应用平台,巨大运算量势必带来采样周期长、开关频率低等问题,从而导致电机转矩脉动大、定子电流质量低。
针对上述问题,有学者提出离线优化方法[4],以减轻在线寻优的运算负担。但离线策略存在时效性差及数据片面性等问题,无法直观体现模型预测控制在线滚动优化的优势。另有学者指出可结合调制策略以消除转矩纹波[5],虽效果突出但运算负担并未得到缓解,反而增加了控制系统的复杂程度。
本文针对永磁同步电机PTC系统,结合无差拍(Dead Beat, DB)控制理论[6-7],研究了一种适用于永磁同步电机的无差拍预测转矩控制(Dead Beat Predictive Torque Control, DB-PTC)策略。通过无差拍控制器,所有电压矢量不再逐一参与价值函数的评估,从而缩小了最优电压矢量的筛选范围,减少了在线优化的滚动次数。在降低控制系统运算量的同时,还能获得与PTC相似的控制效果。
1 永磁同步电机PTC
永磁同步电机在转子两相同步旋转坐标系下的连续时域模型为
(1)
(2)
其中:
ψd=Ldid+ψf,ψq=Lqiq
式中:ud、uq,id、iq,ψd、ψq——d-q坐标系下的定子电压、电流和磁链;
Rs——定子电阻;
Ld、Lq——定子d、q轴等效电感;
ωe——转子电气角速度;
Te——电机电磁转矩;
p——转子极对数;
ψf——转子永磁体磁链。
PTC利用功率变换器的离散化本质,通过滚动优化,直接选出使单一价值函数最小的最优电压矢量。因而,利用前向欧拉法可得到k+1时刻的转矩和磁链预测值为
(3)
式中:Ts——采样周期;
k——时刻。
若忽略定子电阻,则k+1时刻的定子磁链幅值为
(4)
模型预测控制中价值函数反映系统控制指标,在两电平逆变器驱动的永磁同步电机PTC系统中,除转矩和磁链两个主控目标外,还要对系统开关频率进行限制,同时还要设置过流保护等,即有
(5)
其中:
(6)
式中:n——预测步数;
Tek+n、ψsk+n——k+n时刻的转矩和磁链预测值;
Q1、Q2——权值系数,表示转矩跟踪和磁链跟踪两个控制目标的相对重要性;
j=1,2,…,7——两电平逆变器可产生的7个开关状态;
Imax——逆变器可输出的最大电流,表示电机在正常工作时其相电流不应大于该阈值。
因此,根据式(5)选出的最优电压矢量均能够保障系统的稳定运行。永磁同步电机PTC结构如图1所示。

图1 永磁同步电机PTC结构
相较于传统直接转矩控制策略,FCS-PTC的优越性在于对逆变器产生的所有电压矢量进行逐一优选。但是,当逆变器可输出电压矢量较多且采样频率较高时,巨大运算量使开关控制信号延迟,从而导致系统性能恶化。图2为传统PTC预测时域过程,预测步数较大(N>1)时,一个采样周期内无法完成对下一时刻预测值的计算。
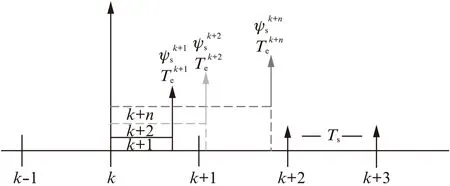
图2 传统PTC预测时域过程
2 永磁同步电机DB-PTC
2.1无差拍电压矢量优选
无差拍控制建立在系统离散模型之上,在一个控制周期内使被控量达到其期望值。在永磁同步电机控制系统中,以电磁转矩和定子磁链幅值的零跟踪误差为控制目标,直接计算出加在定子端的最优电压矢量。
对式(2)求导并离散化可得到用于无差拍控制的系统方程:
(7)
其中:
根据无差拍控制的定义,令Tek+1=Teref,ψsk+1=ψsref;联立式(4)、式(7)可计算得到无差拍控制期望电压矢量udk、uqk。
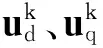
首先,利用Park变换得到定子静止坐标系下的无差拍期望电压矢量:
(8)
则无差拍期望电压矢量所在扇区位置为
通过判断θDB大小即可确定DB-PTC的最优电压矢量选择范围,如图3所示。最优电压矢量的选择范围由传统PTC的7个电压矢量缩小至3个电压矢量,分别为相邻两个有效矢量和一个零矢量。表1为不同扇区传统PTC和DB-PTC对应的最优电压矢量选择范围。

θDB[0,π/3](π/3,2π/3](2π/3,π](π,4π/3](4π/3,5π/3](5π/3,π]SDB123456PTC可选电压矢量000,…,111000,…,111000,…,111000,…,111000,…,111000,…,111DB-PTC可选电压矢量000,100,110000,110,010000,010,011000,011,001000,001,101000,101,100
2.2系统控制结构
对于传统的PTC策略,每一步预测其滚动优化次数始终为7。这种以指数形式增长的计算量势必会加重系统的运算负担。相比之下,DB-PTC每步预测仅滚动3次,预测步数越大,其节省运算资源的效果愈加明显。两种控制策略下多步预测电压矢量的优选过程如图4所示。
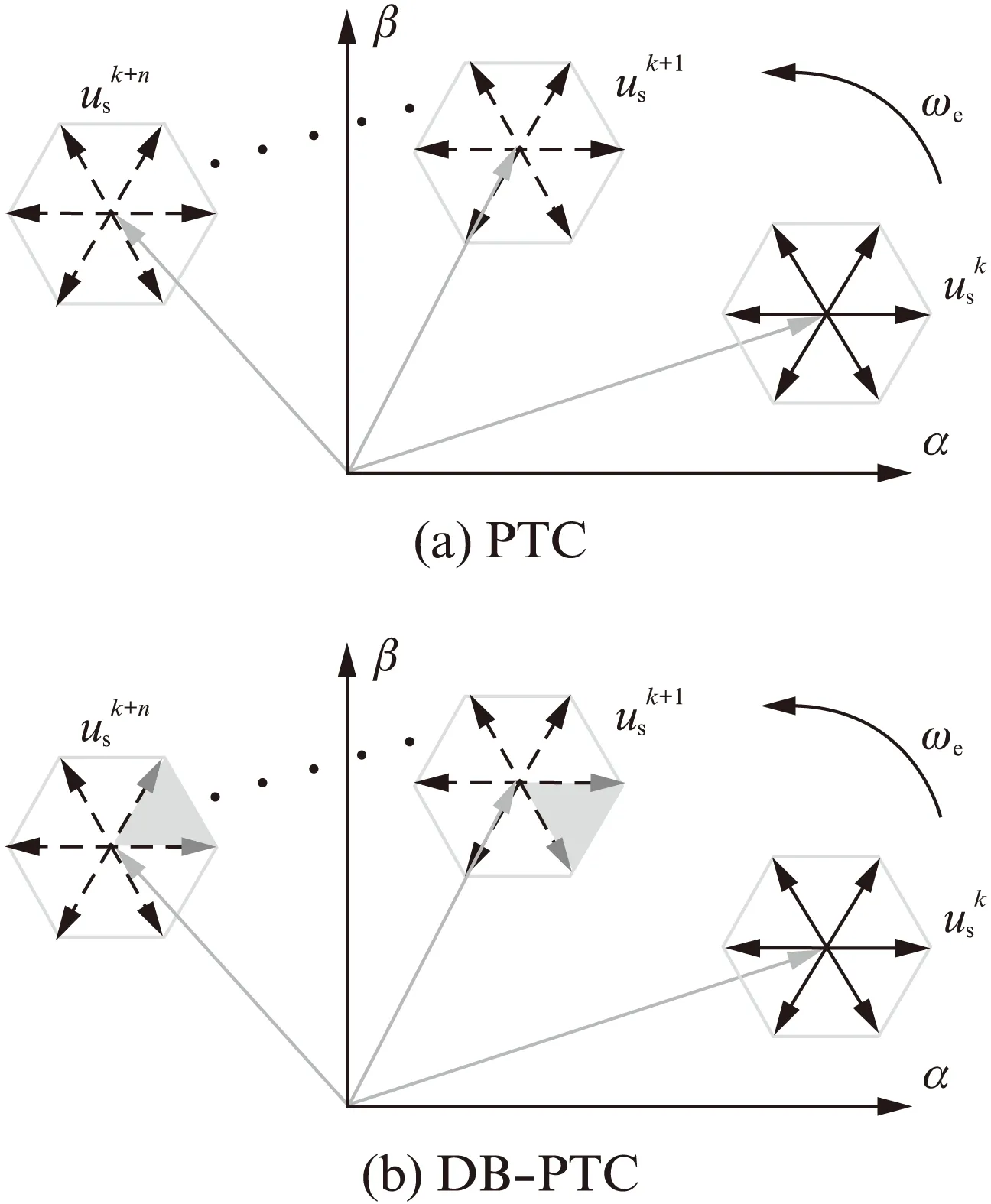
图4 最优电压矢量的选择范围
图5为永磁同步电机DB-PTC结构,与传统PTC结构相比,其增加了无差拍期望电压矢量估测环节和电压矢量优选范围确定环节。

图5 永磁同步电机DB-PTC结构
图6为DB-PTC算法流程图,其中预测步数N=1。由表1可知,在每一扇区对应的可选电压
矢量中总有零矢量的存在。为避免零矢量的漏选,构建了新的电压序列,即[001,000,010,000,011,…,000,001]。即当开关状态i=1时,对应电压矢量001;当i=2时,对应电压矢量000;当i=3时,对应电压矢量010;当i=4时,对应电压矢量000;当i=12时,对应电压矢量000;当i=13时,对应电压矢量001。可以发现,零矢量对应的开关状态均为偶数。同时,对于每一扇区SDB,仅滚动计算3次。
3 仿真分析及试验研究
3.1仿真分析
搭建了基于MATLAB/Simulink的仿真试验平台,对DB-PTC和传统PTC方法进行了仿真对比分析。其中电机参数如下: 定子电阻1.25Ω,d轴电感12mH,q轴电感30mH,转子磁链0.45Wb,极对数为5,额定转速1000r/min。
永磁同步电机DB-PTC系统在不同速度段运行时的响应波形如图7所示。电机初始为静止状态,在0.52s起动后加速运行至额定速度。在该过程中,电机输出额定转矩以便拥有尽可能高的加速度。电机转速达到给定值后经短暂的超调过程进入稳定运行阶段。在2.05s时,给定转速由1000r/min突变至-1000r/min,电机逐渐由正转状态过渡至反转运行。由图7可以看出,在整个运行阶段,电机转速和电磁转矩均表现出良好的跟踪性能,同时定子电流质量很高。
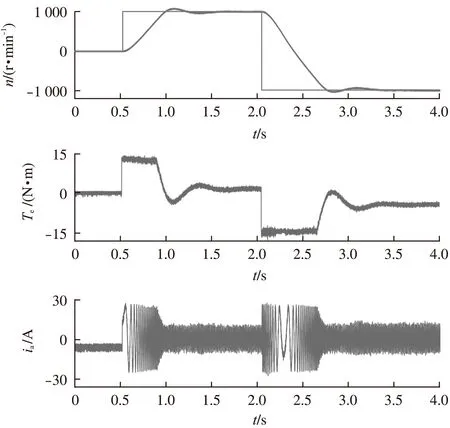
图7 DB-PTC全速域运行结果
图8为电机起动过程传统PTC和DB-PTC两种方法下的开关状态变化对比。由图8可以看出,在转矩阶跃变化过程中,两者动态响应时间都很短,说明DB-PTC继承了PTC优越的动态性能。另外,在暂态响应过程中,两者输出的最优电压矢量均为有效电压矢量,故可保证电机转矩能够以最快速度跟踪参考值。
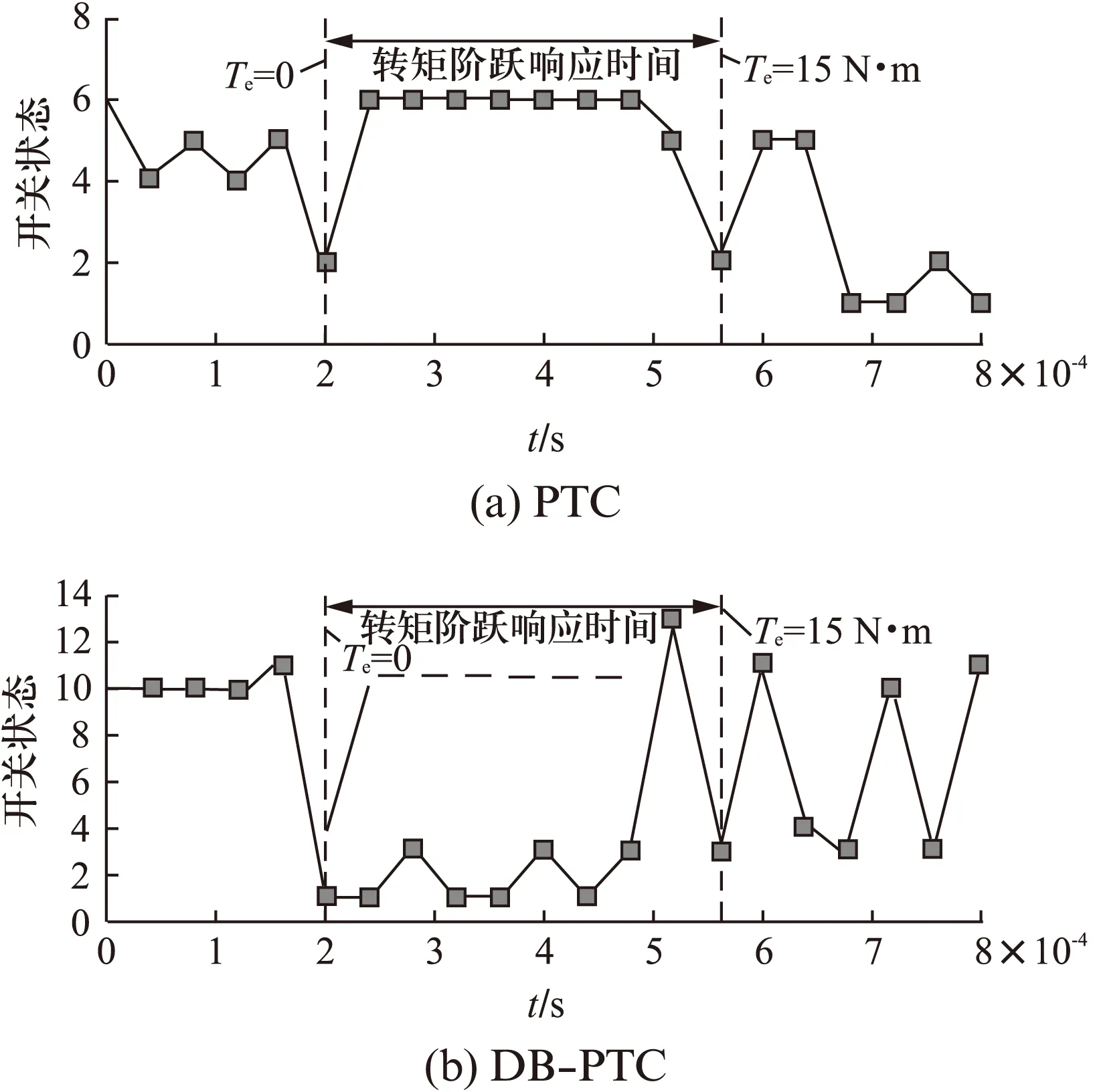
图8 动态性能对比
3.2试验研究
为验证所提方法的性能,搭建了一台内置永磁同步电机试验样机。其轴端与一台直流电机相连,作为负载,电机参数同上。试验平台以TI公司的DSP TMS320F2812为控制核心,控制频率为10kHz。为采用背靠背控制结构,整流模块以二极管为开关器件,逆变模块采用英飞凌公司的BSM10GB170-DLC型IGBT。采用增量式光电脉冲编码器,其分辨率为2048脉冲/r。
图9所示为PTC和DB-PTC两种控制策略下预测算法耗时对比,算法计算时间由DSP的I/O口输出高低电平至示波器测量得到。由图9可以看出,单步预测(N=1)时,PTC滚动计算7次,DB-PTC滚动计算3次,两种控制策略运算耗时接近,均在一个采样周期之内。当预测步数较大(N=2)时,PTC滚动计算49次,而DB-PTC仅滚动计算9次,DB-PTC运算耗时远低于PTC,说明所研究的DB-PTC策略在降低系统运算负担方面有突出效果。
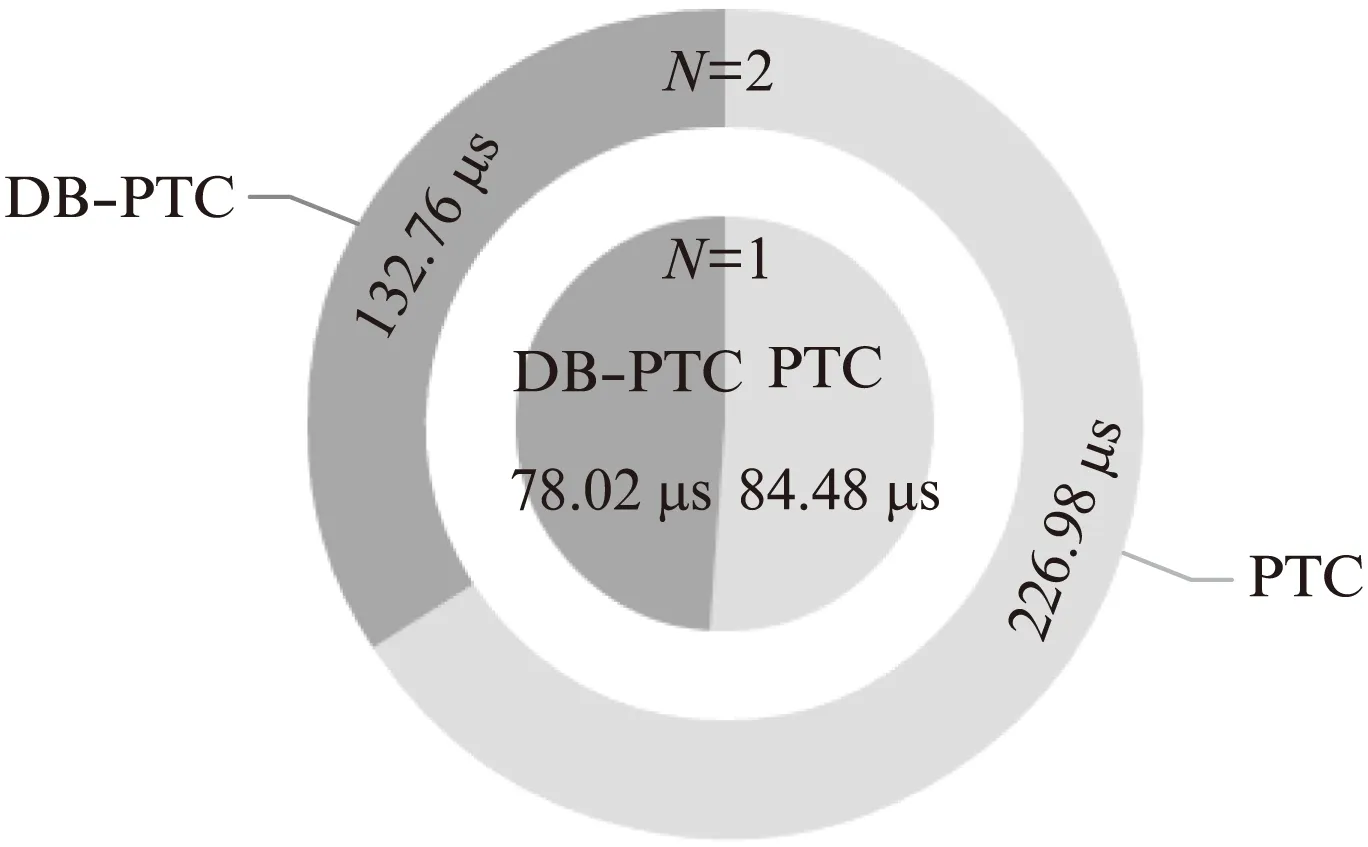
图9 两种控制策略算法耗时对比
图10为电机稳态运行时的转矩和a相电流波形,图11为负载扰动下的定子电流和转矩波形。从其试验结果可以看出,DB-PTC方法具有与传统PTC方法类似的动、稳态性能,表明了所提方法的有效性和可行性。
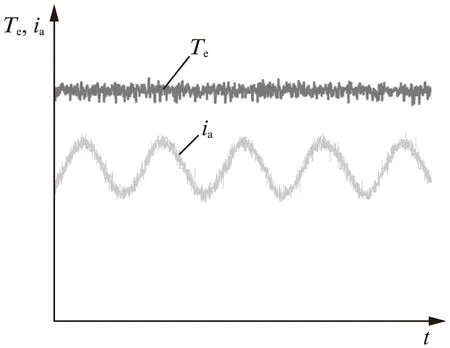
图10 稳态试验结果
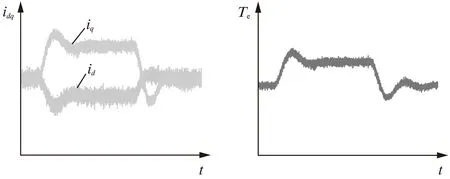
图11 负载扰动试验结果
4 结 语
本文研究表明,DB-PTC策略能够明显降低传统PTC策略在线滚动优化运算量。通过判断无差拍期望电压矢量所在空间位置,缩小了逆变器输出最优电压矢量的筛选范围,从而减轻了系统的计算负担。试验结果验证了所提方法的有效性,同时所提方法具有与传统PTC类似的动、稳态性能,因此在某些应用场合可将其取而代之。
[2]王晶鑫,姜建国.基于预测算法和变结构的矩阵变换器驱动感应电机无差拍直接转矩控制[J].中国电机工程学报,2010,30(33): 65-70.
[3]席裕庚,李德伟,林姝.模型预测控制——现状与挑战[J].自动化学报,2013,39(3): 222-236.
[4]STOLZE P, TOMLINSON M, KENNEL R, et al. Heuristic finite-set model predictive current control for induction machines [C]∥2013 IEEE ECCE Asia Down Under, Crown Conference Centre, Melbourne, Australia, 2013: 1221-1226.
[5]ZHU H, XIAO X, LI Y. Torque ripple reduction of the torque predictive control scheme for permanent-magnet synchronous motors[J]. Industrial Electronics IEEE Transactions on, 2012,59(2): 871-877.
[6]王斌,王跃,王兆安.无速度传感器的永磁同步电机无差拍直接转矩控制方法[J].电机与控制学报,2014,18(6): 42- 49.
[7]孙丹,陈殷,林斌.基于集成观测器的PMSM无差拍直接转矩控制系统[J].浙江大学学报(工学版),2015(6): 1079-1086.
Predictive Torque Control with Dead Beat Solution for Permanent Magnet Synchronous Motor*
PULongmei1,ZHANGHongli2
(1. Xinjiang Vocational and Technical College of Construction, Urumqi 830000, China;2. College of Electrical Engineering, Xinjiang University, Urumqi 830000, China)
A control strategy of finite control set model predictive torque control with a deadbeat solution for permanent synchronous magnet motor drives was presented. By solving the desired voltage vector of deadbeat control and identifying which sector it was located, so the optimal range of output voltage vector was narrowed. For one step prediction based on a two-level inverter, the frequency of receding horizon optimization was reduced from seven to three compared with traditional predictive torque control strategy. For long steps prediction, the effect of cutting down computation burden was more significative .The Simulink and experimental results showed that the proposed strategy had a excellent dynamic and steady state performance similar with predictive torque control strategy. Moreover, the amount of computation was reduced.
dead beat control; predictive torque control; computation burden; receding horizon optimization
国家自然科学基金项目(51575469)
浦龙梅(1973—),女,硕士,讲师,研究方向为电气自动化。
张宏立(1973—),男,博士,副教授,研究生导师,研究方向为智能控制、机器学习等。
TM 351
A
1673-6540(2016)08- 0021- 05
2016-03-02
