寄生蝇声源定位机制分析
2016-10-26侯艳丽纪学军夏克文
侯艳丽,纪学军,夏克文
(1.中国电子科技集团公司第五十四研究所,河北 石家庄 050081;2.河北科技大学 信息科学与工程学院,河北 石家庄050018;3.河北工业大学 电子与信息工程学院,天津 300401)
寄生蝇声源定位机制分析
侯艳丽1,2,3,纪学军1,夏克文3
(1.中国电子科技集团公司第五十四研究所,河北 石家庄 050081;2.河北科技大学 信息科学与工程学院,河北 石家庄050018;3.河北工业大学 电子与信息工程学院,天津 300401)
奥米亚棕蝇尺寸微小,其两耳间距与寄主声音信号的波长极不匹配,却能在极短的时间内利用双耳接收的声音信号对其寄主声源实现精确定位,针对奥米亚棕蝇的惊人定位能力展开研究,分析其定位机制。在奥米亚棕蝇听觉系统力学模型的基础上,建立其数学模型,求解其频域响应,并利用模态分解方法求解两侧鼓膜的时域瞬时响应。通过理论计算和仿真分析了两鼓膜的振动特性,仿真结果表明,奥米亚棕蝇的定位能力要归功于其独特的耦合听觉结构,该结构能放大双耳接收声音信号的强度差和时间差、且随着入射角的变化而变化,从而实现了极短基线的高精度定位。
奥米亚棕蝇;声源定位;耦合结构;模态分解
0 引言
人类和较大型动物对声源的定位主要是由于其头部对入射声波具有一定的散射作用,使到达其双耳的信号存在强度差和时间差,且不同方向上的声源信号会使双耳处于不同的响应状态,双耳就像一对信号差异接收器,中枢神经系统对上述差异进行反应从而实现对声源的定位。奥米亚棕蝇是一种生存在北美的寄生蝇,其尺寸极其微小——听觉器官的跨度约为1.2mm、两耳间距仅450~520μm,为了繁殖后代,怀孕的雌性奥米亚棕蝇必须准确地将其幼虫放置在活野生蟋蟀身上,蟋蟀在夜间寻求交配时所发出的叫声是雌性寄生蝇唯一的定位线索。蟋蟀发出声音的波长约为7cm,与寄生蝇的双耳间距在几何尺度上严重失配,到达寄生蝇双耳的声音信号具有几乎相等的强度和微小的时间差。按照动物的常规声源定位机理,寄生蝇无法实现寄主声源定位,但生物学研究表明寄生蝇能够凭借其独特的听觉系统准确地判断蟋蟀所处的位置[1]。试想一下,如果寄生蝇的听觉系统能实现时间差或强度差的放大,使放大后的效果与大尺寸的动物差不多,那么将能实现精度定位。
R.N Miles等构建了能描述奥米亚棕蝇听觉系统的力学模型[2]。在此力学模型基础上,文献[3-7]对基于寄生蝇的声源定位系统进行了研究。本文在奥米亚寄生蝇听觉系统力学模型的基础上,分析其数学模型、两侧鼓膜的时域振动特性和频域特性,进而分析和总结其定位机理,为寄生蝇的定位机理在声源定位乃至电磁波源测向方面[8-9]的应用提供理论依据。
1 听觉系统的数学模型
研究表明,寄生蝇的双耳不是独立的,其两鼓膜通过膜间桥在中心枢突处形成机械耦合相连,该耦合连接使得两鼓膜接收到的声压信号不仅对自己产生响应,对另一侧鼓膜也产生响应,进而使离声源较近的鼓膜产生较大的反应,离声源较远的鼓膜产生较小的反应,使得两侧响应具有一定的差异[10]。
R.N Miles等人构建的奥米亚寄生蝇听觉系统力学模型如图1所示[2]。在该模型中,将膜间桥看成由刚性系数为k3、阻尼系数为c3的扭转弹簧进行耦合连接的2段钢梁,膜间桥两侧的所有运动部位看成有效的集中质量m1和m2,将膜间桥两端的鼓膜、与鼓膜相连的表皮内突、球状听神经等考虑成弹簧-阻尼对(k1,c1)和(k2,c2),考虑两耳的对称性,有m1=m2=m,k1=k2=k,c1=c2=c。
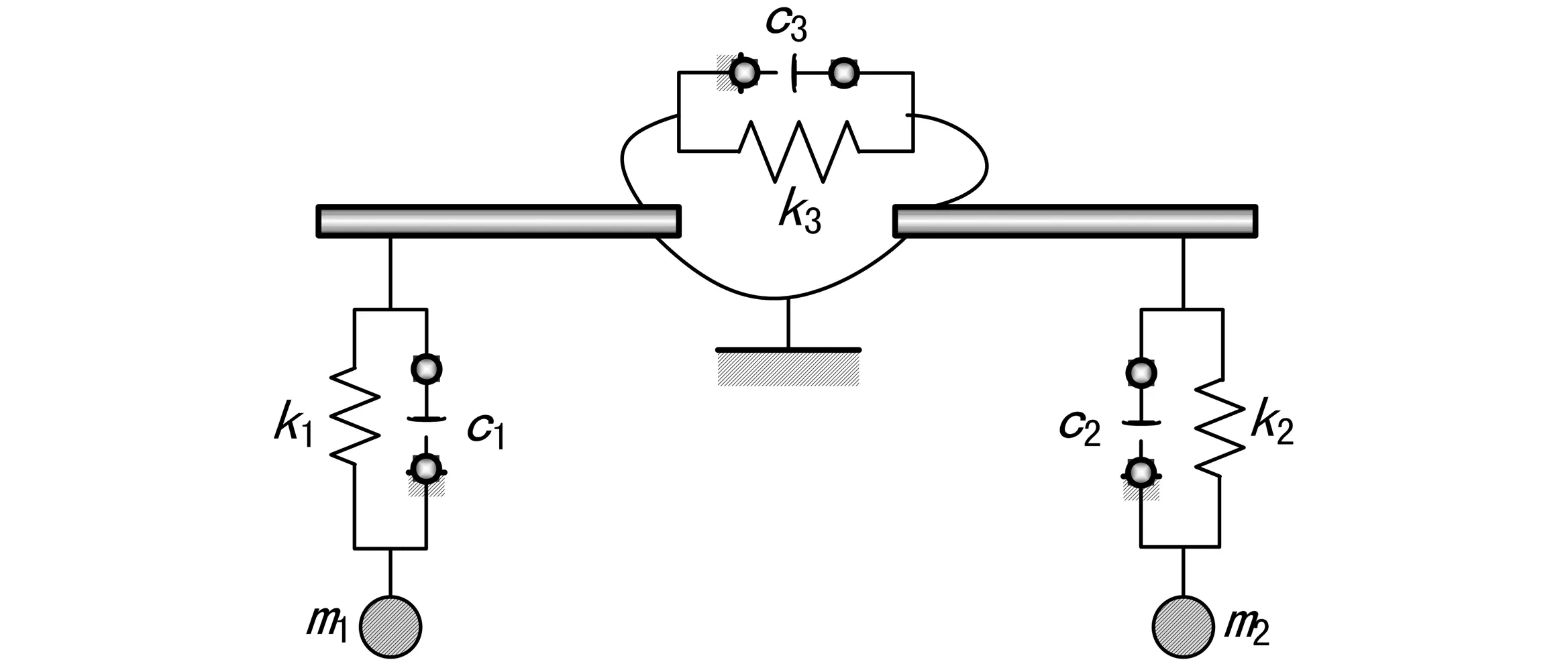
图1 奥米亚棕蝇听觉系统的力学模型
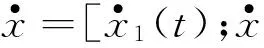
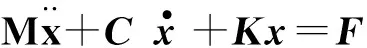
(1)
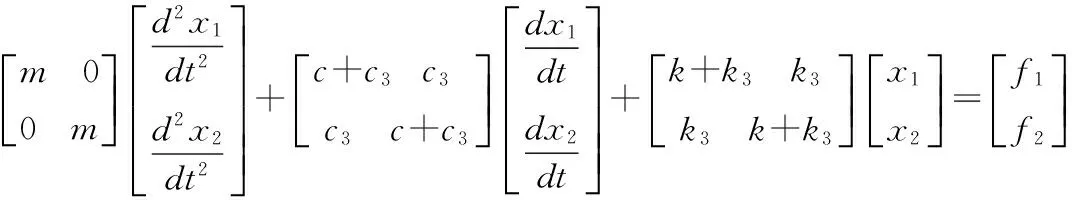
(2)
依据式(2),奥米亚寄生蝇听觉系统可以看成是一个两输入-两输出系统,作用在两鼓膜的声压信号为两输入,两鼓膜的振动位移为两输出。且k3和c3的存在,使两鼓膜间不再是独立的,而是存在着耦合连接,想要确定两鼓膜间是如何相互作用的,需要求解式(2)中的二阶微分方程组。
2 系统的频域响应
将式(1)进行傅里叶变换得:
[(jω)2M+(jω)C+K]X(ω)=F(ω)。
(3)
则奥米亚寄生蝇耦合听觉系统的传递函数矩阵为:
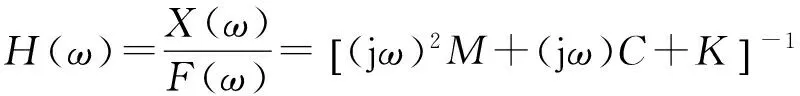
(4)
式(4)中右上角的“-1”表示矩阵求逆运算。
令f1(t)=δ(t),f2(t)=f1(t-τ),则F1(ω)=1、F2(ω)=e-jωτ。其中τ表示声程差在两鼓膜间产生的传输延时,τ=dsin(θ)/c,d为两鼓膜间距,θ为声波入射方向与寄生蝇身体轴向的夹角,c=344m/s为声波的传播速度。则两鼓膜的振动位移响应为:

(5)
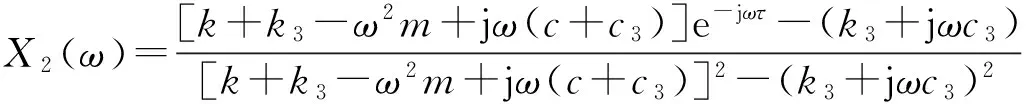
(6)
将式(5)除以式(6),得
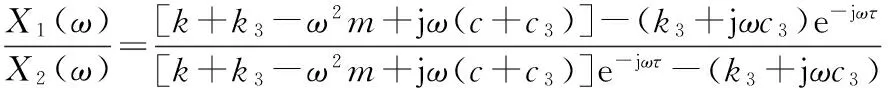
(7)
由式(7)可以看出,两输出响应具有一定的幅度差和相位差。为了使结果看起来更加直观,下面采用模态分解法求解该系统的时域响应。
3 模态分解法求解系统响应
采用模态分解法求解系统响应的思路是:对物理坐标进行变换,得到模态坐标,将两存在耦合的微分方程转化为2个独立的微分方程再进行求解[11-12]。
考虑比例阻尼系统,即
C=αM+βK。
(8)
已知模态阵型具有关于质量矩阵和刚度矩阵的正交性,由式(8)可知,模态阵型关于阻尼矩阵也具有正交性,于是有

(9)
式中,Φ为模态阵型;I为单位阵;ωi和ξi分别为第i阶模态的无阻尼自由振荡频率和阻尼比。奥米亚棕蝇听觉系统的自由度为2,所以有1≤i≤2和1≤j≤2,设奥米亚棕蝇听觉系统的模态阵型为:
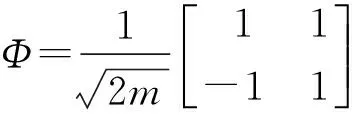
则有
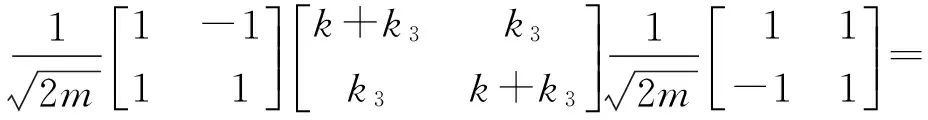
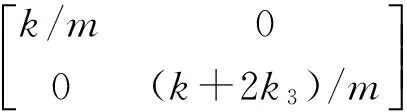
(10)
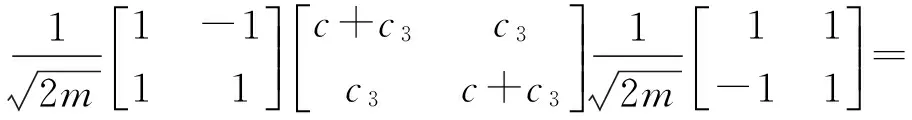
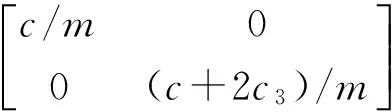
(11)
根据式(9)、式(10)和式(11),得到一阶、二阶模态的自由振荡频率和阻尼比分别为:
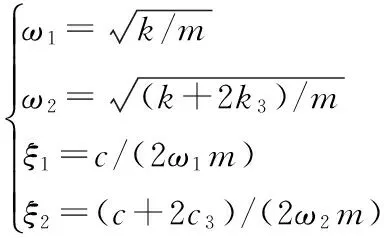
(12)
由式(12)可以看出,系统参数决定振荡频率和阻尼比。利用模态阵型,对物理坐标进行坐标变换:
x=Φη。
(13)
式中,η=[η1,η2]T是模态坐标向量。
将式(13)代入式(1)得:
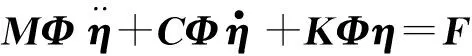
(14)
将上式左乘ΦT,有
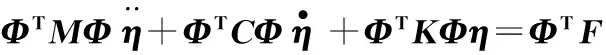
(15)
经化简有
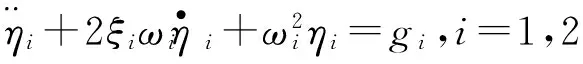
(16)
式中,ΦTF=[g1;g2]。存在耦合的2个物理坐标方程转换成了2个相互独立的模态坐标方程,求出这2个二阶常系数非齐次线性方程的解,再代入到式(13),即可求出物理坐标下的系统响应。
不妨设作用在奥米亚棕蝇中心枢突处的声波激励为Psin(ωt),两侧鼓膜处的压力信号可以写成f1(t)=Psin(ωt+ωτ/2)和f2(t)=Psin(ωt-ωτ/2),则式(16)可以改写成:
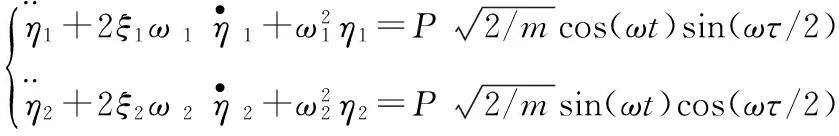
(17)
利用待定系数法求解,可求出
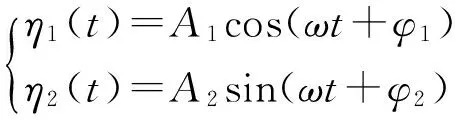
(18)
式中,A1、A2和φ1、φ2分别是两阶模态响应的幅度和相位。

(19)
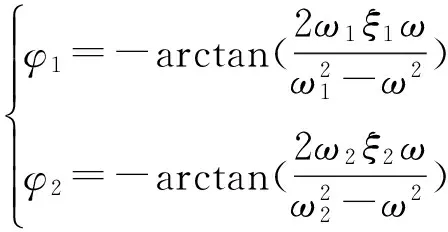
(20)
可以看出两阶模态响应的幅度和相位受控于系统参数;另外,入射波的频率也影响响应的相位;一阶模态响应的幅度取决于两鼓膜所受力的差异,二阶模态响应的幅度取决于两鼓膜所受力的叠加。
由式(13)和式(18),可得物理坐标下的系统响应
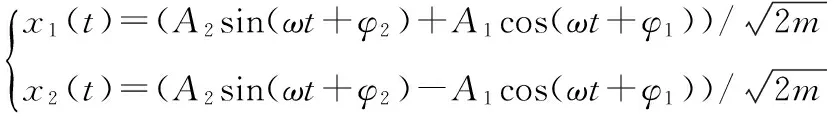
(21)
式(21)中的x1(t)和x2(t)就是奥米亚棕蝇两鼓膜在声激励作用下产生的位移。两侧鼓膜响应是一阶和二阶模态响应的合成,考虑以一阶模态响应的相位为基准,两阶模态响应合成的示意图如图2所示。
图2中,Δφ是两鼓膜响应x1和x2间的相位差,φ12是两阶模态响应η1和η2间的相位差。为方便计算和推导,在图2中设置了5个点O、A、B、C和D,且OB与AD垂直,令∠AOB=β、∠BOD=α,则Δφ=α+β。设响应x1和x2的幅度分别是R1和R2,通过三角形的运算,可以计算两鼓膜响应的幅度和相位差。具体如下:
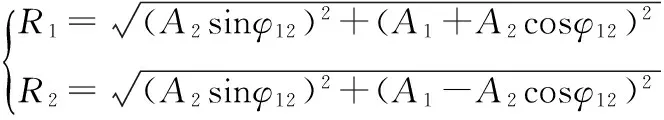
(22)
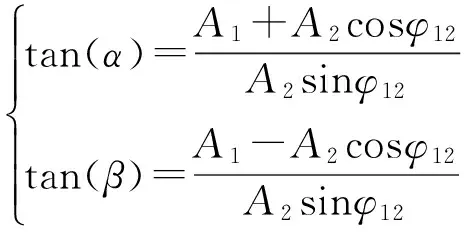
(23)
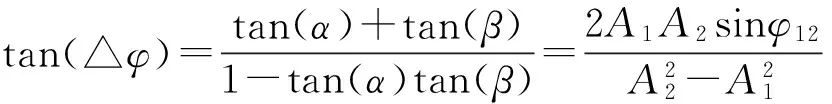
(24)
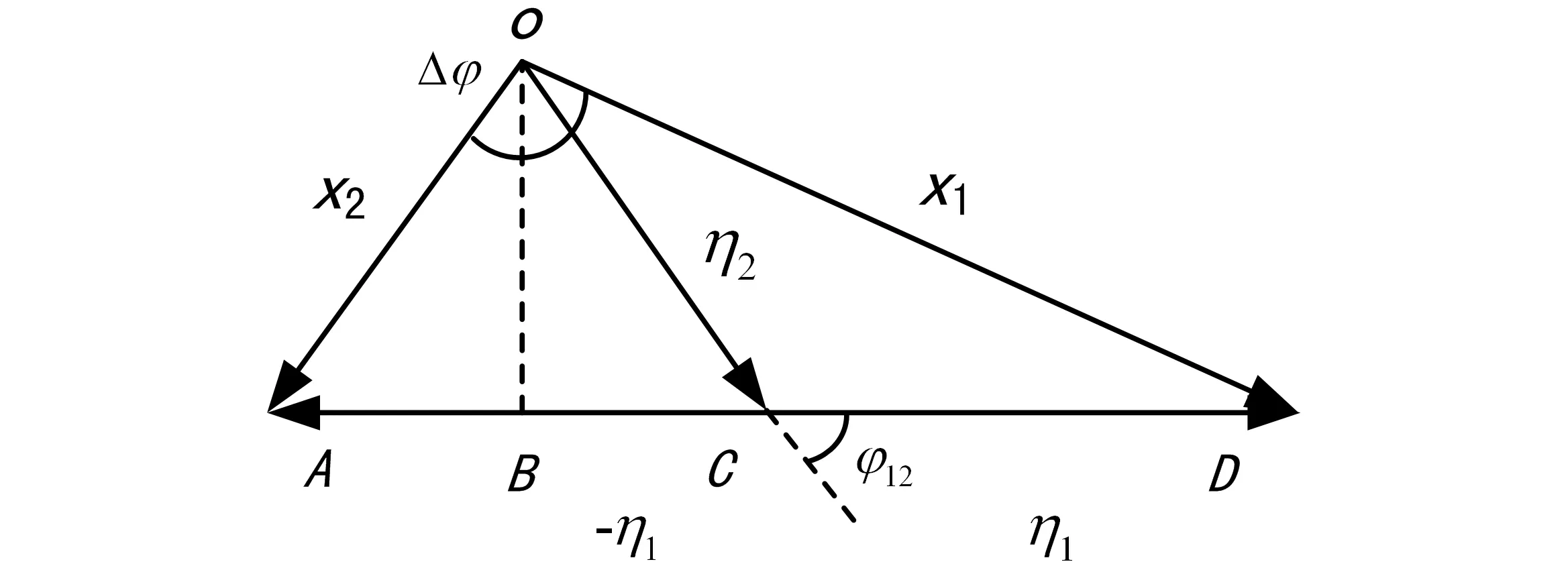
图2 响应的矢量合成
若听觉系统内不存在耦合结构,则 φ12=90°,且A2>>A1,则R1=R2、Δφ很小。有了耦合结构,由图2和式(19)、式(20)可知,φ12≠90°,A1和A2都减少了,但同时二者间的差距被大大缩小了,从而使R1≠R2、Δφ较大,当φ12=0°时有最大相位差,(Δφ)max=180°。可见耦合结构实现了信号间微小差异的放大。
由式(19)、式(20)、式(21)、式(22)、式(23)和式(24)可知,对于某一固定频率的入射波,φ12固定、A1和A2随着入射角的变化而变化,使得两鼓膜响应的幅度差和相位差随着入射角的变化而变化,依据幅度差或相位差与入射角之间的对应关系可以实现声源定位。
4 仿真结果与分析
已知蟋蟀叫声的频率成分单一,约为 5 kHz,寄生蝇听觉系统的跨度约为1.2 mm。依据文献[2]设置耦合结构的参数,m=2.88×10-10kg,k=0.576 N/m,k3=5.18 N/m,c=1.15×10-5N s/m,c3=2.88×10-5N s/m。两侧鼓膜振动位移响应(两侧响应信号)的幅度差和时间差随入射角变化的曲线如图3和图4所示。为便于比较,两侧鼓膜接收信号(两侧输入信号)的幅度差和时间差也被绘制出来。
由图3和图4可以看出,耦合结构放大了两鼓膜响应的幅度差和时间差,且放大后的幅度差和时间差与入射角间具有一对一的函数关系,从而使奥米亚棕蝇可以依据放大后的幅度差或时间差来进行声源定位。
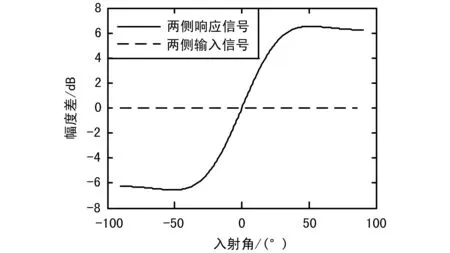
图3 两侧响应的幅度差与入射角的关系曲线
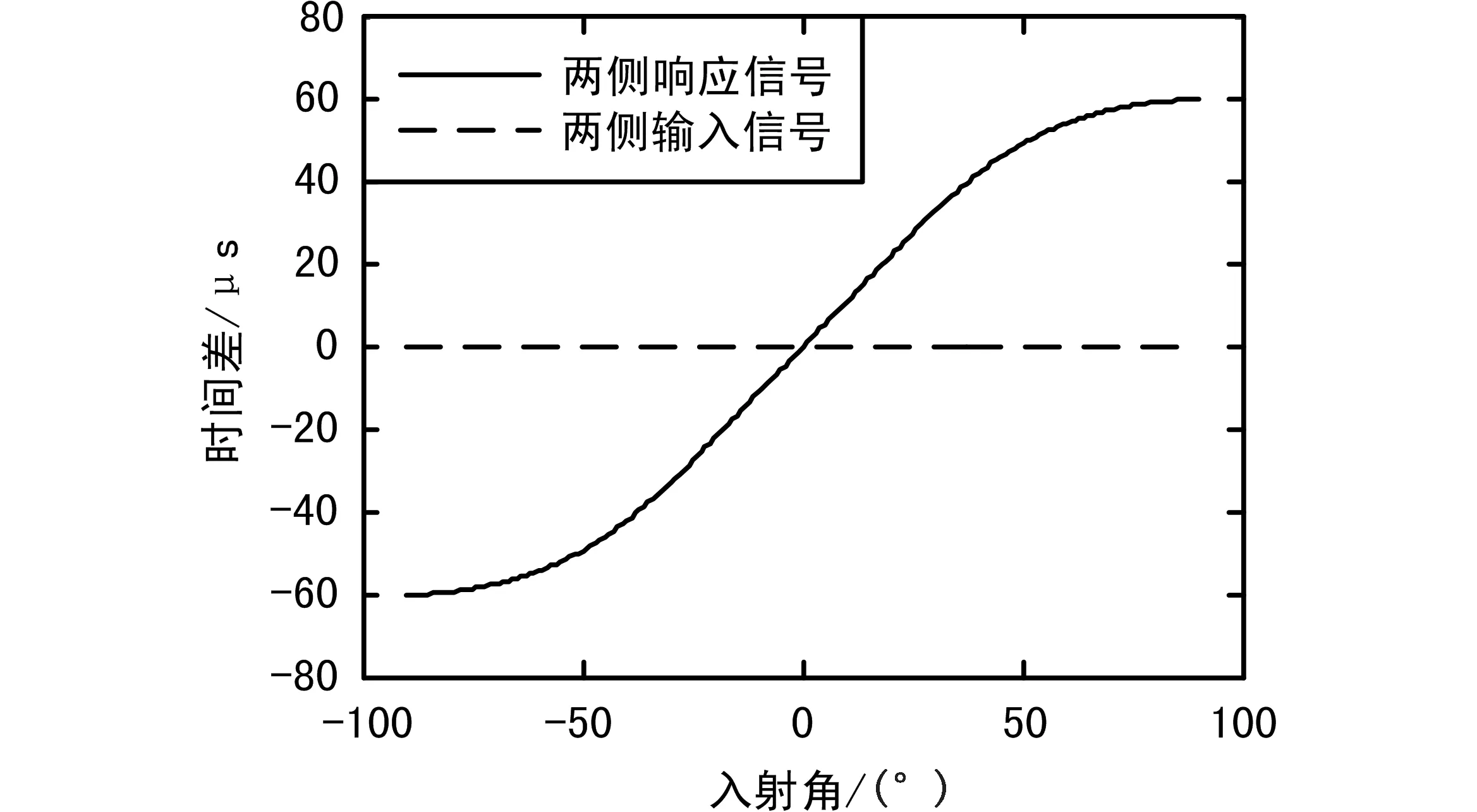
图4 两侧响应的时间差与入射角度的关系曲线
仿真入射角为45°、入射波频率在0~25 kHz变化时,两侧响应的幅度差和时间差曲线如图5和图6所示。
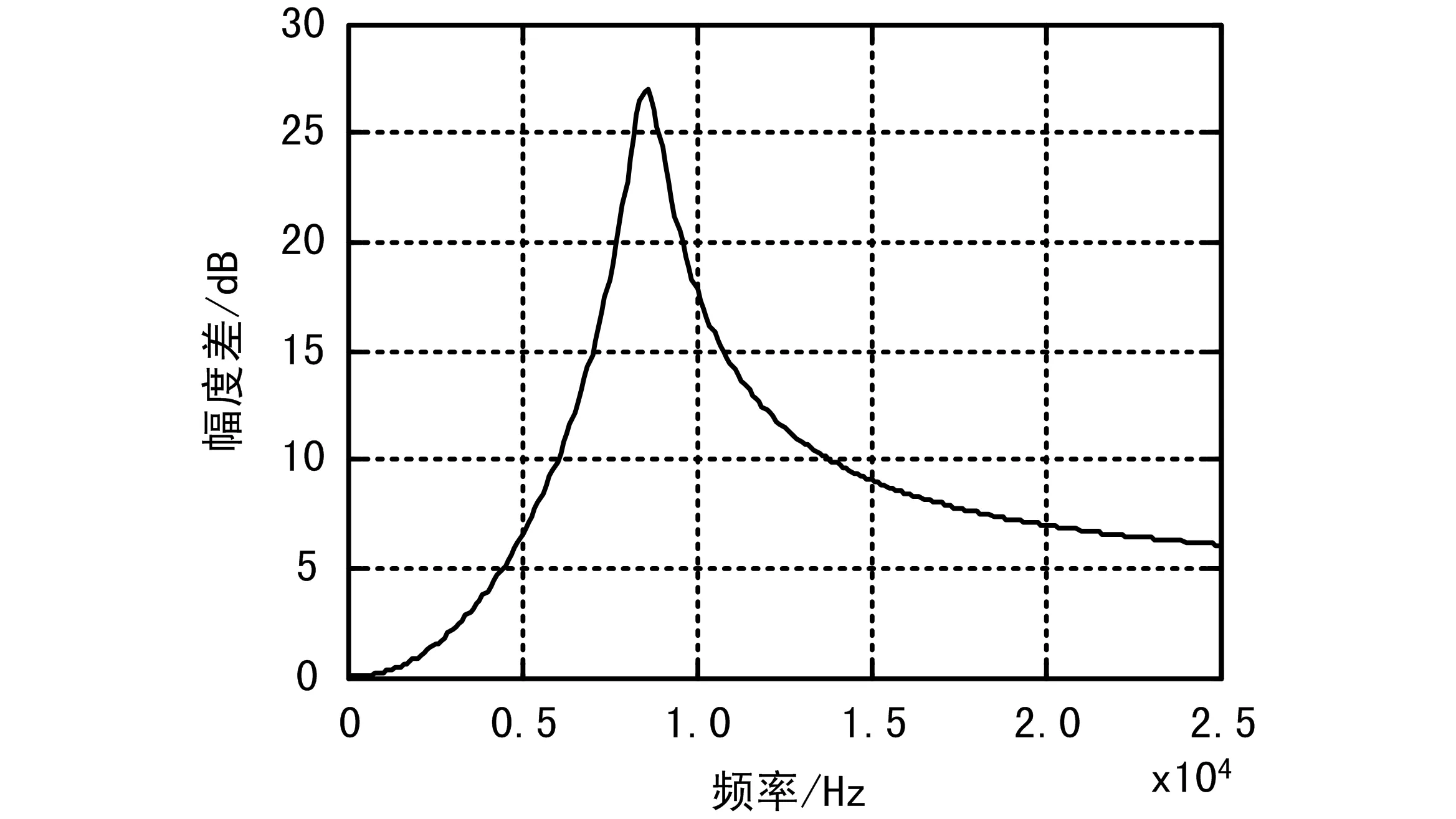
图5 两侧响应的幅度差与入射波频率的关系曲线

图6 两侧响应的时间差与入射波频率的关系曲线
由图5和图6可以看出,不止是5 kHz、对于0~25 kHz的信号,两侧响应的幅度差和时间差都被不同程度地放大,且幅度差和相位差的敏感频段不是完全一致的。
设声压信号为入射角为45°、幅度为1的正弦波,两侧鼓膜接收到的声压信号幅度都为1、时间差为dsin(θ)/λ≈2.5μs,经耦合后两鼓膜的时域瞬态响应如图7所示。
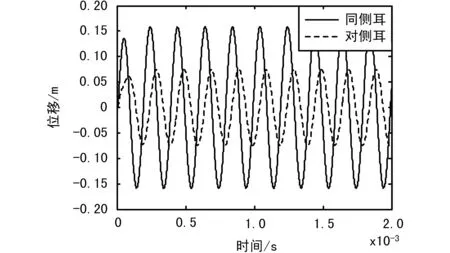
图7 两鼓膜的时域响应
由图7可以看出,在声激励的作用下,两鼓膜响应具有明显的振幅差和时间差;且一旦开始振动,差异立即显现出来;当声波入射角和频率不发生改变时,差异也是恒定的。
从上述仿真可以看出,奥米亚寄生蝇利用膜间桥的机械耦合放大了两侧鼓膜接收信号的时间差和幅度差,并且不同入射方向、不同入射频率时的时间差和幅度差具有明显的变化,奥米亚棕蝇就是依靠这种非线性的耦合放大作用实现寄主声源定位的。
5 结束语
奥米亚寄生蝇双耳间距极其微小,与寄主发出声音的波长严重失配,但它具有一个特殊的听觉结构,能将入射声波信号的微小差异进行放大。通过建立数学模型、进行理论推导和仿真分析,发现该耦合听觉结构能对频率为0~25 kHz、入射角为-90°~90°的声波信号实现不同程度的幅度差和相位差放大。具体地,当耦合结构的参数确定后,放大效果取决于入射波频率和入射方向;对于入射方向确定的单频入射波,被放大的响应差异是确定的;对于单频入射波,响应差异随着入射方向的变化而变化;对于入射方向确定的入射波,响应差异随入射波频率的变化而变化。正是由于这种非线性的耦合放大机制,奥米亚寄生蝇实现了寄主声源的精确定位。模拟耦合听觉系统的动态特性,将其应用在利用幅度差、时间差或同时利用幅度差和时间差的声源定位、电磁波源测向等方面,将在保证精度的前提下实现接收设备的小型化,对于工程应用具有重要的价值。
[1]王庆生.微型生物听觉系统的定向机理及仿生声感应结构的设计与实验研究[D].上海:上海交通大学,2010:9-19.
[2]MILES R N,ROBERT D,HOY R R.Mechanically Coupled Ears for Directional Hearing in the Parasitoid fly Ormia Ochracea[J].Journal of the Acoustical Society of America,1995,98(6): 3 059-3 070.
[3]ACAKAYA M,MURAVCHIK C H,NEHORAI A.Biologically Inspired Coupled Antenna Array for Direction of Arrival Estimation[J].IEEE Transaction on Signal Processing,2011,59(10): 4 795-4 808.
[4]BEHDAD N,LI M,ALJOUMAYLY M.Biologically-inspired Antenna Arrays Based on the Hearing Mechanism of the Parasitoid fly Ormia Ochracea[C]∥2011 IEEE International Symposium on Antennas and Propagation,pokane,Washington,2011: 1 526-1 529.
[5]MASOUMI A R,YUSUF Y,BEHDAD N.An Improved Architecture for Two-element Biomimetic Antenna Arrays[J].IEEE Transactions on Antennas and Propagation,2013,61(12): 6 224-6 228.
[6]杨铭,朱鑫磊,张雅琼,等.基于奥米亚棕蝇听觉定向机制声定位系统仿生学设计[J].中国科技论文,2014,9(8): 870-873.
[7]XU H P,XU X Y,JIA H,et al.A Biomimetic Coupled Circuit Based Microphone Array for Sound Source Localization[J].JASA Express Letters,2015,138(3): 270-275.
[8]塔娜.奥米亚寄生蝇听觉定位机理及其动力学特性研究[D].上海:上海交通大学,2007:34-38.
[9]杨忠.一种基于干涉仪体制的机载测向技术研究[J].无线电工程,2010,40(12): 58-60.
[10]李东虎.干涉仪测向系统中的基线配置技术[J].无线电工程,2014,44(4): 17-19.
[11]张相庭,王志培,黄本才.结构振动力学[M].上海: 同济大学出版社,1994:61-120.
[12]徐斌,高跃飞,余龙.MATLAB有限元结构动力学分析与工程应用[M].北京:清华大学出版社,2009:26-50.
侯艳丽女,(1981—),博士,讲师。主要研究方向:无线电测向。
纪学军男,(1966—), 研究员。主要研究方向:通信对抗。
Analysis on Sound Source Orientation Mechanism of Parasitoid Fly
HOU Yan-li1,2,3,JI Xue-jun1,XIA Ke-wen3
(1.The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China;2.InstituteofInformationScienceandEngineering,HebeiUniversityofScienceandTechnology,ShijiazhuangHebei050018,China;3.SchoolofElectronicandInformationEngineering,HebeiUniversityofTechnology,Tianjin300401,China)
Though ormia ochracea has very tiny size,and its interaural distance and the wavelength of sound signal are severely unmatched,it can locate its specific host for the parasite (cricket) in a remarkably short period of time by the sound signals arriving at its two ears.According to the surprising ability of ormia ochracea,its orientation mechanism is studied and analyzed.Based on the mechanical model of ormia ochracea’s auditory structure,its mathematical model is established,its responses in frequency domain are concluded,and the time transient responses of two eardrums are computed by mode decomposition.The vibrating characteristics of both ends are analyzed by theoretical computing and simulation.The experimental results show that the orientation ability of ormia ochracea owes to its unique coupled auditory structure,which can amplify the interaural intensity difference (IID) and interaural time difference (ITD) that change with the incident angle of sound source,so the high-accuracy localization with short baseline can be achieved.
Ormia ochracea;sound source orientation;coupled structure;mode decomposition
10.3969/j.issn.1003-3106.2016.10.08
2016-07-01
河北省高等学校科学技术研究基金资助项目(ZD2015033,QN2015126);河北省科技支撑计划基金资助项目(14210309D-1)。
TN929
A
1003-3106(2016)10-0033-05
引用格式:侯艳丽,纪学军,夏克文.寄生蝇声源定位机制分析[J].无线电工程,2016,46(10):33-37.
