基于观察学习的概率分布预测模型研究*

吕宗磊　陈国明

(1.中国民航信息技术科研基地　天津　300300)(2.中国民航大学计算机科学与技术学院　天津　300300)



基于观察学习的概率分布预测模型研究*

吕宗磊1,2陈国明2

(1.中国民航信息技术科研基地天津300300)(2.中国民航大学计算机科学与技术学院天津300300)

论文结合松弛属性约束和生成虚拟数据的思想,提出了基于观察学习的概率分布预测模型。传统上观察学习主要用于单点预测和分类问题,论文将观察学习机制应用到小样本集下的概率分布预测问题。该模型利用松弛属性约束分离出数据子集,三次样条插值的方法构建基学习器,并借助虚拟数据使各基学习器达成一致。为了更好地应用模型,给出了信任度设定方法,完善了算法的退出机制。在人工数据和UCI公共数据集的相关实验表明,基于观察学习的概率分布预测模型解决了小样本集下的概率分布预测问题,且优化置信度后的算法具有更好的泛化能力和更高的精度。

观察学习算法; 概率分布; 小样本问题; 虚拟数据生成

Class NumberTP311

1　引言

如何预测概率分布是机器学习领域中常遇到的一类问题,与单点预测相比,概率分布预测可以更精确地刻画数字特征,如置信度、置信区间等。概率分布是描述随机变量的一个有效工具,广泛应用于各领域,如雷电流幅值[1]、风速趋势检测[2]、生物多聚体系统[3]等。通常样本集足够大时,分组统计频次可近似替代概率分布函数。然而在一些新兴领域,数据本身不足或者获取数据的代价过高,不可避免地在小样本集上研究概率分布。

小样本问题(Small Sample Size Problem,SSSP)是一个广泛存在的问题,在人脸识别[4]、语音情感识别[5]和3D动态手势个性化交互[6]等领域备受关注,也是当前学术研究热点之一。许多领域的研究结果表明,松弛属性约束条件[7]和生成虚拟数据[8]是克服小样本问题的有效思路。Li Der-Chiang等综合考虑松弛属性约束和生成虚拟数据的方法提出了基于遗传算法的虚拟数据生成方法[9]。Zhang Cuicui等提出了一种基于泛化学习的集成框架,该框架基于泛化分布产生新数据以缓解小样本问题的影响[10]。Jang Min等提出观察学习算法[11],该算法生成的虚拟数据既用于扩充样本集,又促使各学习器之间互相学习并达成一致,最终提高了算法的泛化能力。但这些方法主要针对数值预测,并不能直接作用于概率分布。

为了预测小样本集的概率分布问题,本文采用松弛属性约束的思想扩充有效样本,采用改进的三次样条拟合的概率分布作为基学习器。将观察学习机制拓展到概率分布集成问题上,完善了概率分布预测模型的参数设置和退出机制。

2　观察学习原理

观察学习(Observational Learning)概念最早来自于1971年Bandura的社会学习理论[12],其核心思想是观察者可以仅通过观察榜样的行为而自己不需要实际模仿,就能够在日后表现出新的行为。1999年Jang Min将该思想引入到集成学习领域并提出了观察学习算法(Observational Learning Algorithm,OLA)[11]。OLA采用生成虚拟数据的方式模拟观察者学习榜样的过程,这些虚拟数据中隐含了达到学习目标的辅助规则信息。随后将观察学习应用到多储层渗透率预测[13],在训练数据不充足的情况下仍然取得了良好的应用效果。2002年,Jang Min在原始的观察学习的基础上,进一步优化了虚拟数据生成策略并分析了虚拟数据提高回归算法泛化能力的原理。同时得出结论,OLA在集成的多样性和平均误差方面均优于其他集成学习算法[14]。

观察学习主要包括准备过程(P-step)、训练过程(T-step)和观察过程(O-step)。以回归模型为例,原始的观察学习采用BP神经网络作为其基学习器。在P-step设定学习器的数目k并采用Bootstrapping方法从数据集D中提取出相应子集D1,D2,…,Dk。在T-step通过子集Di训练选定的学习器模型Li(如BP神经网路);由于各个学习器并没有强制要求类型相同,因此观察学习机制也能拓展到异构集成学习问题。在O-step,实质是各个学习器Li提取其他学习生成虚拟数据的过程。在回归模型中学习器先进行“-i”集成,即不含学习器Li的组合[14]。然后在真实样本附近增加服从正态分布的随机数,由集成后的模型生成虚拟样本,并添加到子集Di为新一轮训练做准备。最后不断重复训练-观察-再训练过程,直至结束。

原始观察学习并没有规定停止训练的条件,只是经过充分大的训练次数G后,停止观察学习,将不同的新学习器按照一定比例(通常相同比例)组合成最终模型并输出结果。其基本训练框架如算法1所示,其中Step1～Step3是准备过程,Step4是准备过程,Step5～Step6是观察过程。

算法1观察学习集成框架

输入:数据集D,基学习器模型L1,L2,…,Lk输出:最终模型LGStep1:Li,i=1,2,…,k表示集成学习框架中的k个基学习器模型。Step2:Di,i=1,2,…,k表示用bootstrapping方法从原始数据集D中抽取的子集。Step3:G表示不断训练观察的次数,t=0Step4:对于每一个学习器Li,i=1,2,…,k,根据子集Di训练学习器Li的参数。参数由各自基学习器类型不同,形式有所不同,但在集成模型中必须有相同的目标输出。Step5:对于每一个学习器Li,i=1,2,…,k,虚拟数据产生方式如下:Lt-i=∑kj=1,j≠iβijLtj其中Ltj表示第j个学习器在第t次迭代时的模型;βij表示第j个学习器对第i个学习器的虚拟数据生成的影响因子;Lt-i表示第t次迭代后的“-i”集成的模型。第t次循环生成的虚拟数据Dti结合相应的输出由Lt-i根据某种虚拟数据生成策略生成本次迭代的虚拟数据Dti。Step6:更新子集Di=Di∪Dti,t=t+1Step7:如果t⩽G,返回Step4;否则,执行Step8。Step8:输出LG=∑ki=1αiLGi,算法结束。

在Jang Min工作的基础上,Yu Fan等将观察学习机制从同构集成模型推广到了异构集成模型,并分析了观察学习提高分类性能的原因[15]。陈曦等提出了一种“基于学习成果优异度加权”的观察学习算法,克服了机场噪声监测点关联预测中小样本引起的欠拟合问题[16]。但这些预测并不涉及对概率分布的集成。文献[17]将观察学习拓展到预测概率分布,并分析了异构集成学习下的该概率分布预测模型同样适用,但其置信度的设置依赖经验并不通用,且多学习器退出机制理论并不完善。

3　基于观察学习的概率分布预测算法

小样本集下的概率分布预测问题主要研究在一组约束条件下目标属性的概率分布问题。所谓小样本并不单纯指样本总数少,而是指满足约束条件,与研究目标相关的有效样本少。出现这种情况也容易理解:之前收集的数据并不是针对当前研究的。因此,面对一个有效样本少、相关数据丰富,同时存在无关数据的样本集不可避免。针对此,提出了一种可行的概率分布预测算法。

3.1准备过程

数据集是条件属性和目标属性的笛卡尔积的子集,即D=A1×A2×…×As×T,其中s为条件属性个数,T为目标属性。条件集C是约束条件的集合,预测概率分布实质是研究满足特定条件集下的概率分布函数。

定义1有效集

数据集D中选择所有满足条件集C的记录,其目标属性值构成的集合称为有效集,记作σC(D)。

其中有效集是多重集,允许有重复元素。例如表1数据集D在条件集C={A1=a,A2=b,A3=c}下的有效集σC(D)={2,2,4}。

表1　数据集D

当条件集C下的有效集足够大时,采用传统方法拟合概率分布函数,然而有时有效集很小,无法满足算法要求。数据集一方面有效样本少,另一方面存在大量相关样本,松弛属性约束的目标在于如何利用这些“不太有效”样本。

松弛属性约束的本质是牺牲一定的精度,增强算法的泛化能力。以条件集C为例,同时满足三个约束条件的样本小于阈值ξ时,可以降低要求,选取同时满足两个约束的样本。以此类推,若样本数仍然小于ξ时,只选取满足一个约束条件的样本。逐步松弛过程如图1所示。松弛的程度取决于原始数据集大小和阈值的选择:当初始数据集过小时或阈值过大,会导致条件集松弛为空集,此时无意义;当初始数据充足但阈值过小时,不需要松弛属性约束,即大样本情况下,可以采用传统统计方法直接拟合。

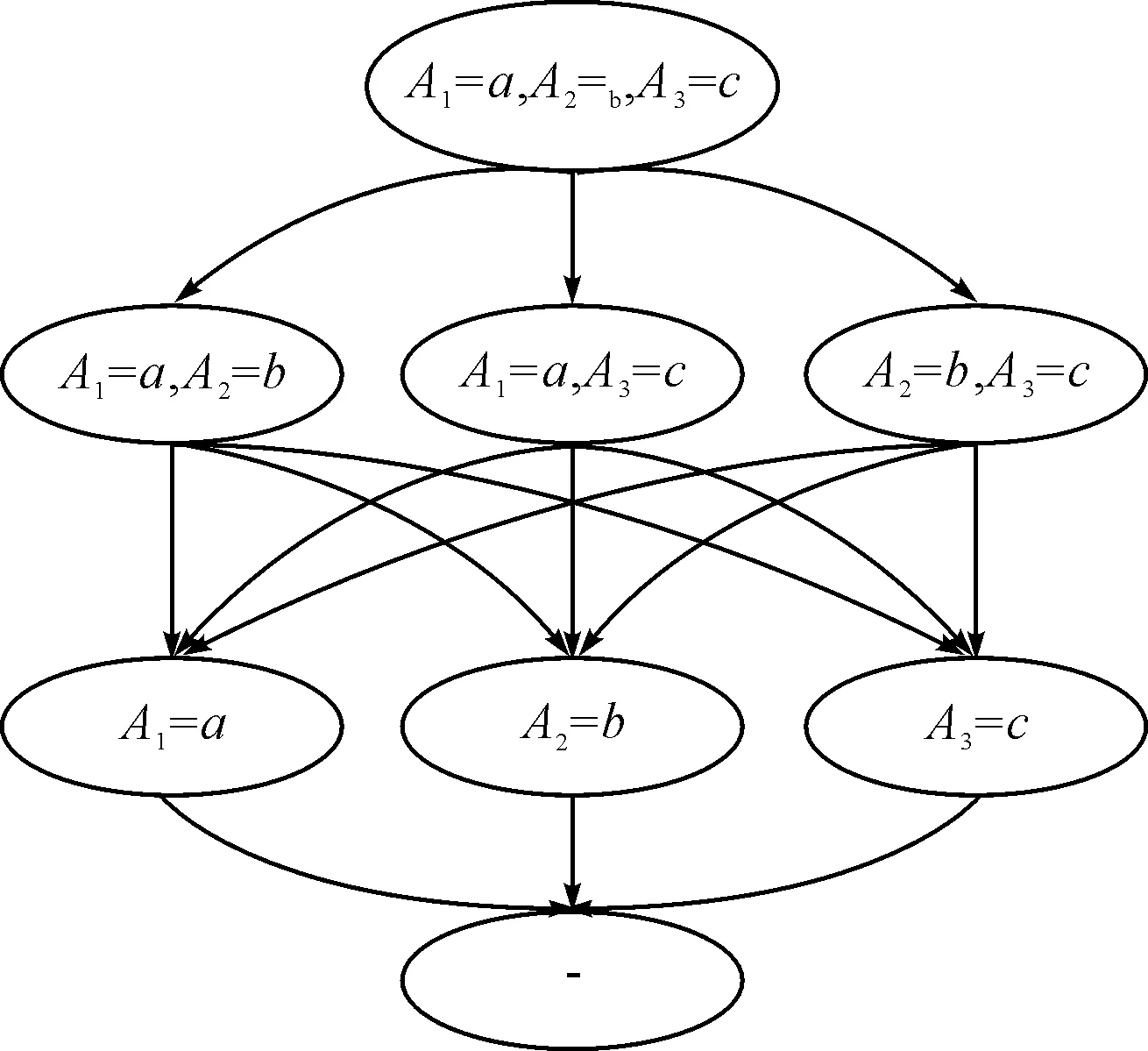
图1　逐步松弛条件集的过程

确定松弛条件集后,如何抽取数据子集是准备过程的重要一步。在观察学习的回归模型中采用Bootstrapping的方法抽取子集,该方法认为各个学习器本质上是无区别的,抽取哪些样本点也没有区别,只需构建出相应学习器即可。然而在小样本下的概率分布预测并不适合。这里学习器数量等于松弛属性后新条件集的个数,因而各个学习器代表的含义并不完全相同,这里抽取的子集Di设定为各自条件集下的有效集。

不同条件集下的有效集下会产生不同的概率分布函数。每个概率分布函数都在一定程度上代表最终概率分布,但真实的分布只有一个。也就是说,如何用多个条件分布组合出最终分布是核心问题,观察过程将详细介绍如何组合最终分布。

3.2训练过程

训练过程实质是将离散的点集拟合出概率分布函数。这里考虑两种情况:一种情况是根据数据背景已知这些数据的分布类型,如正态分布。然后根据最大似然原理计算未知参数。另一种情况是不知道参数类型,这种情况在新问题中更常见。考虑到多项式函数能够逼近任意形式的函数,因此多项式插值是可行的方法。

插值的方法有多种,如拉格朗日插值、分段插值等,但高次多项式差值容易产生Runge现象,分段线性插值不能保持光滑性。一种较理想的方式是采用三次样条插值,既可以保持分段插值的稳定性,又可以保证插值函数的光滑性。

式(1)为分段三次样条插值结果,其中xi为插值点,ai、bi、ci、di为待定系数i=0,1,…,n。

(1)

考虑到分布函数上的每一点都应该为正数,而标准的三次样条插值方法无法保证插值点处为正数的条件下,整条曲线也为正数。为此对插值函数进行调整,要求插值函数不仅过插值点,而且在插值点的一阶导数为零。第i段的调整结果如式(2)所示。

(2)

训练阶段的学习器既可以是基于参数学习或基于非参数的插值函数,也可以是二者混合。因此,基于观察学习的概率分布预测模型同样适用于异构集成。

3.3观察过程

观察过程主要通过生成虚拟数据,使各个概率分布逐步趋于一致。在回归模型中,可以通过文献[14]中的“-i”集成方式组合新学习器生成虚拟数据;但由于概率分布模型的各个学习器代表的含义不同,因此,虚拟数据应根据各自分布特点自行产生。虚拟数据体现了学习器的观点,但学习器接受其他观点的程度是不同的。为此给出信任度的定义。

定义2信任度

令A和B是两个学习器,所谓A对B的信任程度θAB就是指一个0～1之间的实数来表示每一次A接受B观点的程度。

为了便于分析,假设A对B的信任程度与A、B自身的观点之间是独立的,即θAB和θBA不必相等,也不必满足特定约束。事实上,信任程度可以看作是一个在学习器进行讨论前就已经存在的先验知识。因此,A对B的信任程度可以看作是一个常数。

在概率分布模型中,每个学习器都代表一组约束下的分布函数,因此属性间的数量关系反映了两个学习器间的信任程度。因此,定义第i个学习器对第j个学习器的置信度如式(3)所示。

(3)

其中,Ci,Cj表示松弛后对应第i个和第j个学习器的条件集。信任度决定了观察过程中一个学习器吸收其他学习器产生虚拟数据的比例。另一个问题是虚拟数据如何生成。

虚拟数据可以是服从各自概率分布的随机数,只要数目足够多就能够代表自身分布。但若每个学习器按照自身模式随机生成,无法保证最终概率分布的一致性。为此,虚拟数据的另一部分随自身概率分布特点固定的产生虚拟点。两种虚拟数据生成的数据集可以由V1+αV2表示,其中V1=σ1(f,N),表示随机生成N个服从f的虚拟数据,V2=σ2(f,N),表示固定生成N个服从f的虚拟数据,α为比例函数,初始为0,随迭代次数的增加逐步增加到1。

这种混合生成虚拟数据的机制,既保证了算法的泛化能力,又保证了算法的收敛性。特别的当α≡1时,相当于几个概率分布的组合输出。

3.4退出机制

在回归模型中,并未给出退出训练-观察的条件,当学习器观点一致,或者当分布函数差异度为零时,则可以代表数据集下的泛化分布函数。分布函数的差异度是指任意两个概率分布函数差的积分值,如式(4),或者用1-Div〈fi,fj〉/2表示二者的相似性。为了提高运算效率,迭代过程采取统计随机点的均方误差来衡量两个分布的差异,如式(5),其中x1,x2,…,xm为随机点。

(4)

(5)

若任意两个分布的差异度都小于退出阈值ζ后,则任意分布函数都是最终的泛化分布函数。算法2给出了基于观察学习的概率分布预测模型的完整运算过程。

算法2基于观察学习的概率分布预测模型

输入:数据集D,条件集C,阈值ξ,退出阈值ζ输出:最终模型fStep1:比较|σC(D)|和ξ,若|σC(D)|<ξ,则松弛C,并比较每一个子条件集|σCi(D)|和ξ,直至对每个条件集都有|σCi(D)|⩾ξ;此时对应的条件集分别为C1,C2,…,Ck。Step2:从数据集中抽取子集Di=σCi(D),其中i=1,2,…,k。Step3:计算信任度矩阵θ,其中每个元素的计算方法如下θij=|σCi∪Cj(D)||σCj(D)|Step4:用三次样条插值方法将子集Di拟合概率分布函数fi其中,i=1,2,…,k。Step5:for(i=1;i⩽k;i++)begin for(j=1;j⩽k;j++) D*j=σ1(fj,θij|D|)+ασ2(fj,θij|D|) Di=Di∪D*i endStep6:更新后的子集Di拟合新的fi,i=1,2,…,k。Step7:随机生成m个随机数x1,x2,…,xm。并计算DivDiv=max1⩽i,j⩽n∑mk=1(fi(xk)-fj(xk))2。Step8:若Div>ζ回到Step5,否则下一步。Step9:输出结果一致的概率分布f,算法结束。

其中Step1～Step3是准备过程,寻找有效集的复杂度为O(kn),其中n表示样本数目,k表示属性个数;当k不大时,松弛属性约束的过程可以视为常数。Step4～Step6是训练-观察-再训练过程,其复杂度主要受到生成虚拟数据个数的影响,观察-训练的迭代次数与退出阈值ζ相关。Step7～Step9判断算法是否终止并输出最终分布,其时间复杂度为O(m),其中m为随机数的个数。

4　实验结果与分析

为了验证基于观察学习的概率分布预测模型的有效性,选取样本充足的人工数据及UCI上的公共数据集,设计了以下几组实验。

实验一:三次样条插值效果分析。实验随机生成10000个服从正态分布N(0,1)的随机点,然后采用分八段的三次样条插值进行拟合。并检验三次样条插值与标准正态分布的相似性,实验结果如图2所示。

实验表明,用三次样条插值方法得到的正态分布与标准正态分布的相似性高达98.91%。说明在样本充足时,直接通过三次样条插值拟合概率分布是可行的。因此,在未知数据分布的情况下,采用直接三次样条插值获得的概率分布函数作为基准分布是合理的。

图2　三次样条插值效果图

实验二:退出机制分析。选取UCI数据集quake,该数据集包含三个条件属性(震源深度,纬度,经度)和一个目标属性(地震等级)。根据震源深度可以分为浅源地震(60km以下)、中源地震(60到300km)和深源地震(300km以上)。实验输出为中国及周边地区的浅源地震的概率分布,因此条件集为C={0≤focal_depth≤60,4≤latitude≤53,73≤longitude≤135}。为了验证混合虚拟数据生成机制保证最终分布的一致性,设置系数函数α如式(6)所示,其中t表示迭代次数;退出阈值ζ=0.001。迭代过程的差异度如表2所示。

(6)

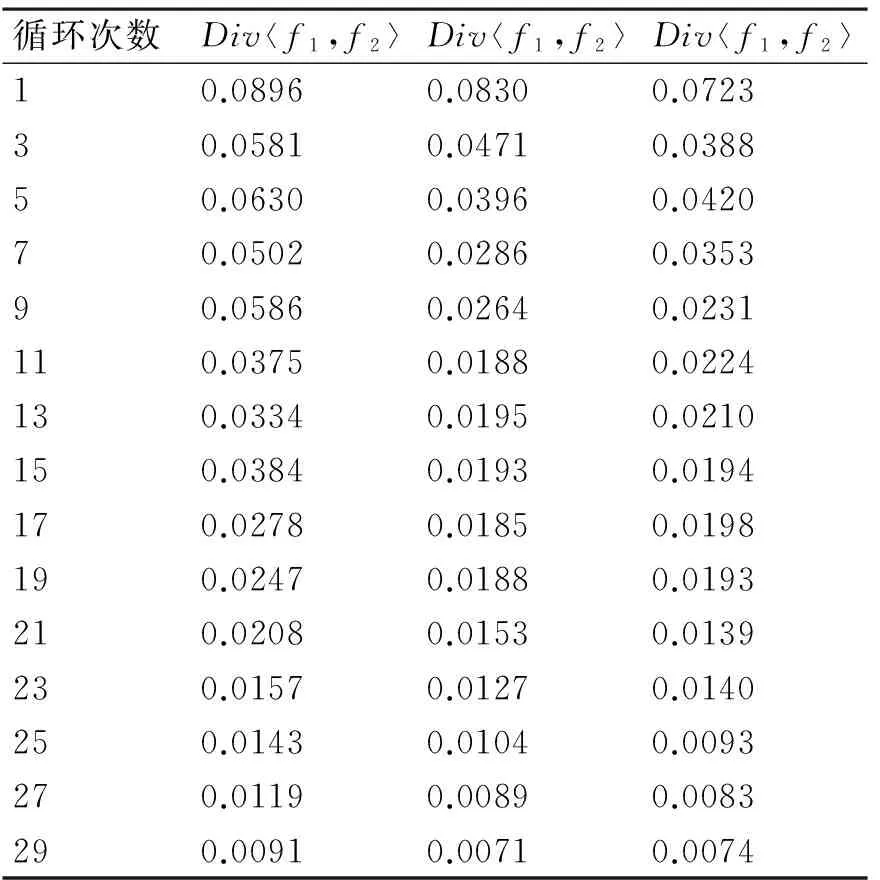
表2　迭代过程表

从表2中可知,在前20次循环时,差异度整体上逐渐减小,由于随机因素的影响,出现个别差异度增大的情况。但随着迭代次数到20次以后,随机因素影响减小,不同分布之间的差异度稳定地逐渐减小,直到趋同。

实验三:验证基于观察学习概率分布预测模型的预测效果。数据集及参数设置与实验二相同,选择直接用三次样条拟合的分布为标准fS,比较概率分布的平均相加fA、置信度参数相同(当i≠j时,θij=0.1;否则,θij=1)的观察学习fO1、改进置信度的观察学习方法fO2。对应的单约束的条件分布曲线(初始基学习器)和最终的分布曲线对比图如图3、4所示。

其中图4中fS与fA、fO1、fO2的相似性分别为86.87%、94.02%,97.76%。该实验结果表明,基于观察学习的概率分布预测模型显著优于概率分布的简单叠加,并且优化置信度后的观察学习算法具有更高的精度。

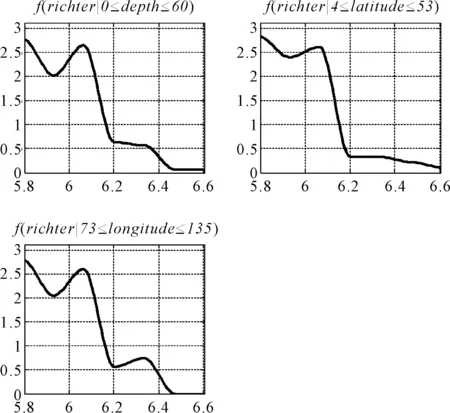
图3　各条件分布图

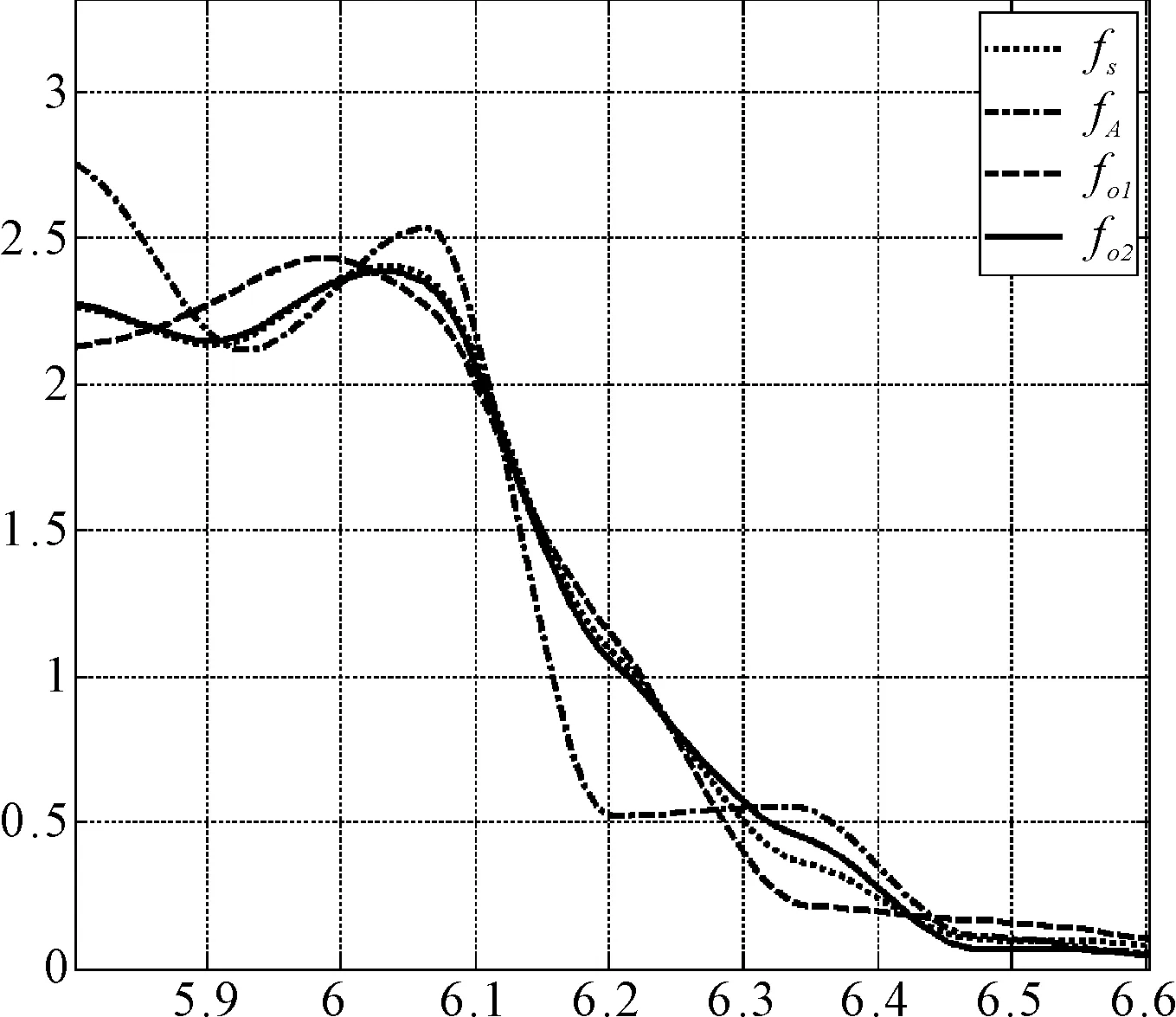
图4　不同方法对比图

实验四:其他数据集上的分析。选取不同属性,不同条件集下的大样本数据集,对改进的观察学习与三次样插值得到的标准分布进行比较分析,结果如表3所示,其中相似性是指实验三中fA与fO2的相似性。

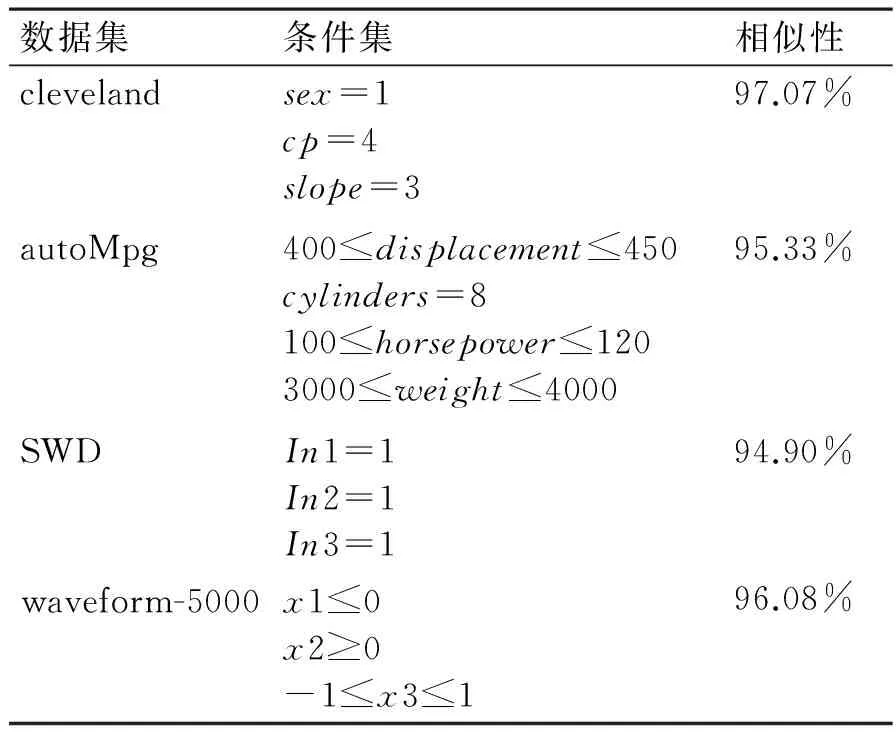
表3　不同数据集的相似性

实验表明,观察学习算法在不同数据集上具有广发的适用性,无论条件集约束是离散属性、连续属性或者混合型的;并且在样本充足时,与三次样条插值算法预测的概率分布具有高度的相似性,基本在95%以上。

5　结语

本文将观察学习集成机制应用到了预测概率分布问题上。该模型利用松弛属性约束和生成虚拟数据的思想极大地扩充了样本集,使其能够应用在小样本数据集上。而后改进了观察学习的置信度参数设置并优化了退出机制。在UCI公共数据集的相关实验表明,基于观察学习的概率分布预测模型解决小样本下的概率分布预测问题,并且在样本充足是其预测结果与三次样条预测的概率分布有95%以上的相似性。

[1] 刘刚,张弦,陈锡阳,等.雷电流幅值概率分布函数的分段拟合方法[J].华南理工大学学报(自然科学版),2014,42(4):40-45.

LIU Gang, ZHANG Xian, CHEN Xiyang, et al. Sectioned fitting method of probability distribution function of lightning current amplitude[J]. Journal of South China University of Technology(Natural Science Edition),2014,42(4):40-45.

[2] Shamshirband S, Petkovic D, Tong Chong Wen, et al. Trend detection of wind speed probability distribution by adaptive neuro-fuzzy methodology[J]. Elsevier,2015,45(10):43-48.

[3] Albert J, Rooman M. Probability distributions for multimeric systems[J]. Journal of Mathematical Biology,2015,72(1-2):157-169.

[4] Wang C P, Zhang J S, Chang G D, et al. Singular value decomposition projection for solving the small sample size problem in face recognition[J]. Journal of Visual Communication and Image Representation,2015,26(10):265-274.

[5] 毛启容,赵小蕾,白李娟,等.结合过完备字典与PCA的小样本语音情感识别[J].江苏大学学报(自然科学版),2013,34(1):60-65.

MAO Qirong, ZHAO Xiaolei, BAI Lijuan, et al. Recognition of speech emotion on small samples by over-complete dictionary learning and PCA dimension reduction[J]. Journal of Jiangsu University(Natural Science Edition),2013,34(1):60-65.

[6] 武汇岳,王建民,戴国忠.基于小样本学习的3D动态视觉手势个性化交互方法[J].电子学报,2013,41(11):2230-2236.

WU Huiyue, WANG Jianmin, DAI Guozhong. Personalized interaction techniques of vision-based 3D dynamic gestures based on small sample learning[J]. Acta Electronica Sinica,2013,41(11):2230-2236.

[7] Yang Y, Wang X Q. Attribute reduction based on the grey relational analysis and dynamic programming[C]//Natural Computation (ICNC), 2013 Ninth International Conference on. IEEE,2013:697-701.

[8] Li D C, Lin L S, Peng L J. Improving learning accuracy by using synthetic samples for small datasets with non-linear attribute dependency[J]. Decision Support Systems,2014,59:286-295.

[9] Li D C, Wen I H. A genetic algorithm-based virtual sample generation technique to improve small data set learning[J]. Neurocomputing,2014,143:222-230.

[10] Zhang C C, Liang X F, Matsuyama T. Generic learning- based ensemble framework for small sample size face recognition in multi-camera networks[J]. Sensors,2014,14(12):23509-23538.

[11] Jang M, Cho S. Ensemble learning using observational learning theory[C]//Proc of the International Joint Conference on Neural Networks (IJCNN),1999:1287-1292.

[12] Bandura. Social leaning theory[M]. General Learning Press. New York, USA,1971.

[13] Wong P M, Jang M, Chos S, et al. Multiple permeability predictions using an observational learning algorithm[J]. Computers & Geosciences,2000,26(8):907-913.

[14] Jang M, Cho S, Observational learning algorithm for an ensemble of neural networks[J]. Pattern Analysis & Applications,2002,5(2):154-167.

[15] 虞凡,杨利英,覃征.异构集成学习中的观察学习机制研究[J].广西师范大学学报(自然科学版),2006,24(4):54-57.

YU Fan, YANG Liying, QIN Zheng. Observational learning algorithm for heterogeneous ensembles[J]. Journal of Guangxi Normal University(Natural Science Edition),2006,24(4):54-57.

[16] 陈曦,王建东,陈海燕.基于观察学习的机场噪声监测点关联预测研究[J].计算机工程与科学,2015,37(2):335-341.

CHEN Xi, WANG Jiandong, CHEN Haiyan. Research on the associated prediction of airport-noise monitoring nodes based on observational learning[J]. Computer Engineering & Science,2015,37(2):335-341.

[17] Lu Z L, Xu T. A new method to predict probability distribution based on heterogeneous ensemble learning[J]. International Journal of Advancements in Computing Technology,2012,4(14):17-25.

Prediction Model of Probability Distribution Based on Observational Learning

LV Zonglei1,2CHEN Guoming2

(1. Information Technology Research Base of Civil Aviation Administration of China, Tianjin300300) (2. College of Computer Science and Technology, Civil Aviation University of China, Tianjin300300)

A new prediction model of probability distribution based on observational learning has been proposed in this paper, which is combined with the concept of loosening control conditions and virtual sample generation. Observational learning algorithm is expanded to research the probability distribution under small sample in this model, which is applied to point prediction and classification traditionally. The model extracts the subsets with loosening attribute conditions and creates base learners with cubic spline interpolation function. The virtual samples are used to promote the consistency of base learners eventually. The model provides calculation formula for trust of learner and optimizes the exit mechanism to apply the model better. The results from manual dataset and real world problems from UCI repository shows that the model solves the problem of probability distribution prediction under small samples and the optimized observational learning algorithm is better and higher in generalization and precision than before.

observational learning algorithm, probability distribution, small sample size problem, virtual sample generation

2016年3月18日,

2016年4月27日

中央高校基本科研业务中国民航大学专项基金项目(编号:3122013z004);中国民用航空科技基金项目(编号:MHRD20140315)资助。

吕宗磊,男,博士,副教授,硕士生导师,研究方向:数据挖掘、机器学习与知识工程等。陈国明,男,硕士研究生,研究方向:数据挖掘、机器学习等。

TP311DOI:10.3969/j.issn.1672-9722.2016.09.002