中国海表面风统计降尺度模型研究

李正泉，肖晶晶，马　浩，冯　涛（浙江省气候中心，浙江杭州310017）

中国海表面风统计降尺度模型研究

李正泉，肖晶晶，马浩，冯涛
（浙江省气候中心，浙江杭州310017）

基于CCMP卫星风场数据和NECP-DOE再分析数据两者典型空间模态近20 a的长期统计关系，构建了中国海域海表面风的统计降尺度模型。降尺度模型交叉验证结果表明：模拟与观测两者风速在空间分布和变化趋势上均具有很好的吻合性，风速空间分布的相关性（R）可达到0.98以上，风速变化趋势的相关性（R）可达0.89以上。模型预测风速的均方根误差（RMSE）和绝对误差（AE），在绝大多数海区均低于0.25 m/s和0.30 m/s，相对误差（RE）＜-5%或＞5%的海区面积仅约占全海域面积的5%左右。从空间上而言，降尺度模型的模拟误差大值区多发生在陆域附近的近海区，主要原因是近海区影响风场的中小尺度天气因子众多。

海表面风；统计降尺度；经验正交函数；CCMP风场；NCEP-DOE

1　引言

大尺度粗网格的气候数据因空间分辨率太低，较难适用于局部区域的气候分析和气候变化研究。降尺度是将大尺度低分辨的空间信息转化为小尺度高分辨率，以使得局部空间信息更加丰富和清晰可辨［1-2］。通常应用的降尺度方法有3种，即动力降尺度、统计降尺度和统计与动力相结合的降尺度［3］。统计降尺度是通过建立大尺度信息变量与小尺度信息变量两者之间的统计关系，将大尺度低分辨率的空间变量带入统计模型，来获取局地变量高分辨率的空间信息［4-5］。由于统计降尺度方法计算量小且简便易行，因此在国内外区域气候的模拟和预估研究中被广泛使用。

利用多元回归构建统计降尺度模型，Sailor等分析了美国局部地区的气温变化［6］，Murphy模拟了欧洲地区的月气温和月降水［7］。采用ANN技术构建统计降尺度模型，Mpelasoka等分析了新西兰的月气温和降水［8］，Bardossy等以模糊规则分类法为基础建立统计降尺度模型，研究了德国和希腊的气温与降水［9］。Goodess等评估了20余种统计降尺度方法在不同气候区不同季节对温度与降水指数的模拟能力［10］。在国内亦有许多研究者利用统计降尺度方法开展区域气候的模拟与预估，如范丽军对华东区气温变化的集合预估［11］、崔妍等对江淮流域极端降水的预估［12］、薛春芳等对渭河流域秋雨的模拟分析［13］、郭彦等我国北方地区降水的季节预测［14］以及阮成卿等对我国西南地区后冬降水的降尺度模拟［15］，等等。从文献调研来看，统计降尺度技术在我国区域气候研究中已有较多应用，但研究对象多针对于气温或降水，而有关风场的统计降尺度分析尚不多见。汤建平等曾利用591个气象站的风能参数与大尺度环流场的统计关系，开展我国风能变化的降尺度模拟预估［16］，但其研究范围仅限于陆域，并未涉及至我国海域，且其研究方法在海域范围内较难实现，原因是海上测风站点稀少，长年代测风数据缺乏，尤其是在远海区域。

本文以卫星观测CCMP（Cross-Calibrated，Multi-Platform）风场为基础，以卫星格点观测代替站点观测，建立高分辨率CCMP风场与大尺度NCEP-DOE变量场两者EOF（Empirical Orthogonal Function）典型模态的多元统计关系，进而构建适合于我国海表面风的统计降尺度模型，意旨为海表面风区域降尺度的模拟预估研究提供一种较为可行的研究方法。

2　资料与方法

2.1使用资料

统计降尺度模型构建和模型验证所使用的资料为1988—2011年CCMP卫星风场数据和NCEP-DOE再分析数据，数据来源于共享网站http: //rda.ucar.edu/datasets/ds744.9/index.html和http: //www.esrl.noaa.gov/psd/data/gridded/data.ncep.reanalysis2.html。CCMP风场是2010年美国国家航空航天局（NASA）发布的交叉定标多平台卫星探测海表面风场资料，它是可覆盖全球范围时空分辨率最为精细的长年代风场数据之一，其空间分辨率为0.25°×0.25°、时间分辨率为6 h（数据时次为00时、06时、12时、18时）。由于CCMP风场融合了多系列数十颗卫星观测资料，因此其风场数据较其它卫星风场在精度上有着很大提高，在诸多海洋大气环境研究中被广泛应用［17］。NCEP-DOE再分析数据是美国国家环境预报中心（National Centers for Environmental Prediction，NCEP）和美国能源部（Department of Energy，DOE）合作研制的全球大气再分析资料（也被称作为NCEP-R2），它相对于NCEP/NCAR再分析数据（NCEP-R1），在较多细节上作出了改进，是NCEP/NCAR再分析数据的更新和订正版本［18］。本文中使用的NCEP-DOE再分析数据是海表面风速（U，V）、海平面气压（Sea Level Pressure，SLP）和海表面温度（Sea Surface Temperature，SST），数据的空间分辨率为2.5°×2.5°、时间分辨率为6 h（数据时次为00时、06时、12时、18时）。

2.2技术方法

根据1988—2011年逐日4个时次的CCMP风场数据和NCEP-DOE再分析数据，计算统计逐年各月的气候要素值。月平均风速（W）的计算过程为：先依据CCMP（U，V）和NCEP-DOE（U，V）的经向纬向风矢量，计算各时次的风速值，再按逐年逐月对

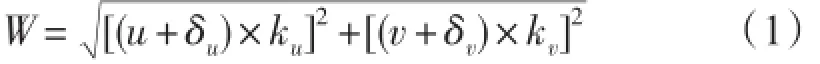
式中：W为风速（m/s），u和v分别为经向和纬向风矢量网格值（m/s），δu和δv分别为经向和纬向风矢量网格值的附加值（Add Offset），ku和kv分别为经向和纬向风矢量网格值的换算因子（Scale Factor）。

以CCMP（W）作为降尺度模型构建的目标变量（空间分辨率为0.25°），NCEP-DOE（W，SLP，SST）作为预测因子变量（空间分辨率为2.5°）。使用经验正交函数（EOF）［19-20］对CCMP（W）矩阵和NCEP-DOE（W，SLP，SST）矩阵进行空间模态分解，基于多元线性回归技术建立CCMP（W）主模态与NCEP-DOE（W，SLP，SST）主模态之间的统计关系，以此构建我国海表面风的统计降尺度模型。

具体步骤是：对给定的CCMP（W）矩阵和NCEPDOE（W，SLP，SST）矩阵，分别移除各自的气候平均态后进行EOF分解，提取各自的空间EOF模态主成分PC，之后按照式（2）的方式，建立CCMP风速与NCEP-DOE变量之间的统计关系。风速值进行统计。各时次风速（W）的计算公式如下：

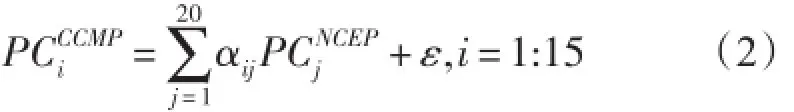
确定出CCMP风速与NCEP-DOE变量之间的统计关系后，按式（3）和式（4）即可将大尺度粗分辨率的气候变量“投影”转化成高空间分辨率的海表面风速。

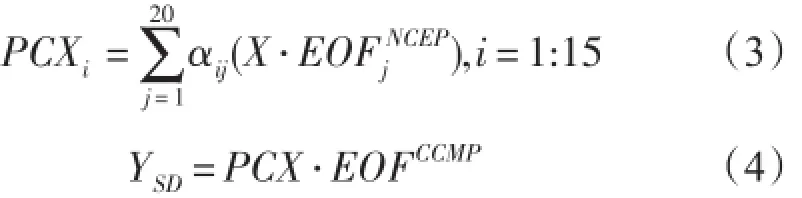
对于统计降尺度模型的效果检验，本文使用了方差贡献（EV）、标准差（SD）、残差标准差（SE）、相关系数（R）、均方根误差（RMSE）、相对误差（RE）和绝对误差（AE）等统计参数，它们的定义及公式较为常见，在此不再累述，具体请参见文献［19］。

3　结果分析

3.1统计降尺度模型构建

我国海表面风统计降尺度模型的构建基于1988—2007年共20 a的长期数据，模型预测的目标变量矩阵为1988—2007年间的CCMP月平均风速（W），预测因子矩阵为1988—2007年间NCEP-DOE的月平均海表面风速、气压和温度（W，SLP，SST）。选用NCEP-DOE（W，SLP，SST）前20个主模态（PC总方差贡献EV约为97.3%）与CCMP（W）前15个主模态（PC总方差贡献EV约为95.6%），按式（2）的形式，进行构建统计降尺度模型。

表1给出了CCMP（W）和NCEP-DOE（W，SLP，SST）前10个主模态的方差贡献（EV）以及回归模型的标准差（SD）和残差标准差（SE）等统计参数。可以看出，目标变量前10个主模态的PC总方差贡献可达到93.5%，预测因子前10个主模态的PC总方差贡献可达到92.5%。目标变量与预测因子回归模型的SE占SD的比重很小，前6个PC的SE占其SD的比重均不足5%。虽然PC10的SE占其SD的比重约为20%，但PC10的方差贡献较小（仅约1.6%），其在统计降尺度模型构建中的实际贡献很少。

3.2模型回算检验

使用1988—2007年NCEP-DOE（W，SLP，SST）数据，按照式（3）和式（4），对海表面风降尺度模型进行回算模拟。比较模型回算风速与CCMP观测风速两者之间的相关性及其模拟误差，对构建的统计降尺度模型进行验证。如图1所示（中国海域范围及海区划分请参见文献［21］），1988—2007年模型回算风速与CCMP观测风速（20 a平均值）的空间分布形态基本完全一致，仅是在东海南部的局部区域上有些细微差别，两者风速分布的空间相关系数（R）达到0.998。各年份模型回算风速与CCMP观测风速的空间相关性，见表2。

在空间各个格点上，模型回算与CCMP观测两者风速年际变化的相关性（1988—2007年期间）和模型回算风速的均方根误差（RMSE）空间分布（见图2）。回算风速与观测风速年际变化的相关系数（R），全海域的格点平均值约为0.93，两者风速的年际变化在格点位相上表现出了非常好的符合。从空间分布来看：远离陆域的远海存在相关系数的高值区（黄海中部除外），尤其是渤海、黄海北部、东海南部、巴士海峡、南海东北部等，该些海域的R值大多均超过0.95，R值最大可达到0.98（见图2a）。

由于远海区影响海表面风场的动力学因素较为简单，缺乏地形等影响，因此相关系数在远海区存在高值；而在陆域近海区，影响风场的因子众多，中小尺度天气过程活跃，风场降尺度模型的误差相对较大，如山东、浙江和广州等近海以及台湾岛附近海区等，这些区域是相关系数低值区，其R值多在0.75以下，但R值低于0.65的海区面积较少（仅约总海域的3%）。从风速均方根误差（RMSE）空间分布看：回算与观测两者风速的RMSE值多在0.25 m/s以下，仅是在台湾岛附近和广州近海岸等一些局部区，RMSE值高于0.40 m/s（见图2b）。

表1　目标变量与预测因子前10个主模态的统计参数

表2　模型回算风速与CCMP观测风速的空间相关性统计

图1　CCMP观测风速与模型回算风速空间分布（虚框内为两者重点差异区）

由图1和图2可知，无论是风速空间分布形态，还是风速变化趋势及风速误差，统计降尺度模型的回算值与CCMP的观测值均表现出了非常好的吻合性，这充分表明了统计降尺度模型的构建合理性。为了进一步验证所构建的降尺度模型其外推预测的可靠性，利用2008—2011年数据再次对降尺度模型进行检验。

3.3模型外推预测检验

基于已构建的海表面风降尺度模型统计关系（采用1988—2007年数据建立），利用2008—2011年的NCEP-DOE变量资料（未参与建模数据），按式（3）和式（4）对海表面风进行降尺度模拟预测。从图3分析，2008—2011年模型预测风速与CCMP观测风速（5 a平均值），两者的空间分布形态十分相似（这与模型回算检验类同），仅是在黄海中部和东海北部的局部区域上有些差别，两者风速空间分布的相关系数性（R）达到0.988，各年份的R值也都在0.980以上（见表3）。

模型预测与CCMP观测两者风速的年际变化，在空间各格点上的相关性R值多在0.90以上，全海域的R平均值约为0.89，这表明模型预测与CCMP观测两者格点上的风速变化趋势具有良好吻合性（见图4a）。总体来说，远离陆域的远海R值较高，近海岸区R值较低，但R值低于0.65的海区面积不足全海域面积的4%，这种R值的空间分布型态与降尺度模型回算的结果大体相似（见图2a），仅是R值大小略有差异，模型回算的R值略高于模型预测。

表3　模型预测风速与CCMP观测风速的空间相关性统计

模型预测误差分析显示，全海域风速预测的RMSE平均值约为0.12 m/s，绝大多数区域的RMSE值均＜0.25 m/s，仅是在台湾岛附近和南海中东部的一些零星区域，其RMSE值＞0.30 m/s（见图4b）。风速预测的绝对误差（AE）在空间各格点上均＜0.50 m/s，全海域平均的AE值约为0.13 m/s，大部分海域的AE值均在0.30 m/s以下，但在渤海、黄海北部、台湾岛附近以及陆域近海岸等一些局部区，风速预测的AE值较高些，约在0.35 m/s以上（见图4c）。从风速预测的相对误差（RE）来看，在我国北部海域（渤海与黄海）、台湾海峡、北部湾及海南岛附近区域等，降尺度模型的模拟预测风速较CCMP观测风速偏低，两者风速的RE值多在-2.0%左右，局部区域可达到-4%以下；在东海大部、南海大部、巴士海峡、台湾岛附近及其以东洋面海域，降尺度模型的模拟预测相比CCMP观测的风速值较高，尤其是在广东、台湾及其它一些陆域的近海区，两者风速的RE值可达到8.0%左右（见图4d），但整体而言，全海域内风速预测的RE值较小，RE＜-5%或RE＞5%的空间格点占有量很少，不足海域总面积的5%。

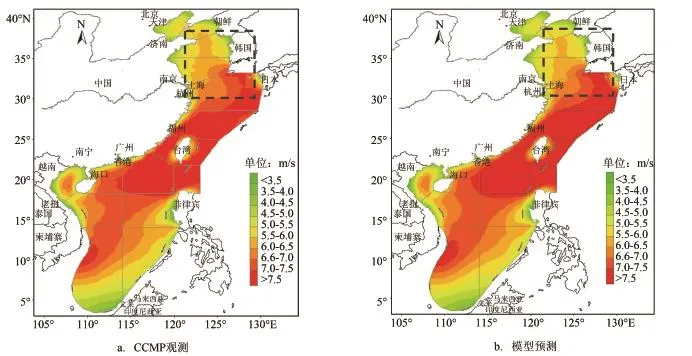
图3　CCMP观测风速与模型预测风速空间分布（虚框内为两者重点差异区）

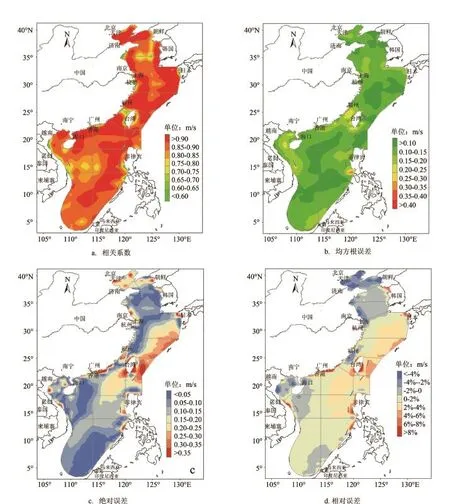
图4　2008—2011年预测与观测风速比较

3.4模型误差原因浅析

降尺度模型回算和模型外推的检验结果均显示，模型模拟风速与CCMP观测风速两者在陆域近海区（尤其是沿海岸区）的差异，相比于远海区要相对大一些。如：近海区风速年际变化的相关性系数（R）值多低于远海区，且风速模拟的RMSE、AE和RE的高值区也多发生在陆域近海。这种误差分布的空间形态是由诸多因素引起的，其中近海与远海风场的动力学因子差异是其主要原因。由于远海区缺乏地形等影响，海表面风形成的动力学因素较为简单，而陆域近海影响风场的因子众多，中小尺度天气过程活跃，CCMP空间分辨率精细对这种中小尺度的天气过程具有很强的捕捉能力，但NCEP-DOE的空间分辨率太粗，中小尺度过程的捕捉能力太弱［19］。

在模型模拟与CCMP观测两者风速年变化相关分析中，值得一提的是尽管黄海中部区并非靠近陆域，但其模拟与观测的风速相关性却是相对较低，R值多在0.80以下，低于其周围海域（见图2a和图4a）。探寻该区R值偏低的原因，海雾影响可作为一种合理解释。黄海是我国海域中海雾最频发的区域，而黄海中部更是黄海海雾的重发区［22］。CCMP风场源于卫星探测，云、雾、降水等天气现象对遥感信号的发送与接受均会造成干扰影响［23］。尽管在风场反演过程中，卫星资料已经过数据除噪处理，但仍无法确保该些干扰区风场反演的准确性。更有甚者当干扰信号过强时就会造成观测缺失，而缺失部分只能由周围的正常观测值插补形成。NCEP-DOE资料主源于地表面（海面）站点观测，基本不受天气条件影响。在海雾频发重发的黄海中部区，CCMP与NCEP-DOE两者观测资料受海雾的影响程度不一，这就可能会引起两者风速的不对应变化。

另一方面，从模型外推的预测检验结果中，可发现在东海中部至台湾以东的远海区分布着一条风速绝对误差（AE）相对较大的带状区域，AE值多在0.25 m/s以上，比其它远海区的AE值都要大些（见图4c），且带状区内的风速相对误差（RE）也相对较高，局部区的RE值可在4%—6%之间（见图4d）。这种有别于其它远海的误差分布，其原因可能归结于该区台风活动影响。影响我国海域的台风多生成于菲律宾以东洋面，按台风路径主要分为西进型、登陆型和转向型3类［24］。西进型台风主要影响我国南海海域，登陆型和转向型台风多影响我国浙江至广东一带的东部海域（包括台湾两侧海域）。西进型台风在移动路径中因受菲律宾陆域阻挡，至我国南海时风力多会有所减弱；而登陆型和转向型台风移至浙江至广东一带的东部远海（含台湾两侧海域）时，一路无地形遮挡，风力十分强大，且随台风逐渐向大陆靠近或受台湾岛阻挡时，风力又会有所减弱。Hoffman等研究指出［25］，在风速低于16 m/s的情况下，CCMP资料的风速误差值较为稳定，但随风速进一步增强，CCMP的风速误差值会明显扩大。由此推断，台风活动频繁且风力强度大，可能是引起东海中部至台湾以东一带远海区模型模拟误差偏大的一个重要原因。

4　结论

本文基于1988—2007年CCMP卫星风场数据和NECP-DOE再分析数据两者典型空间模态的长期统计关系，构建了我国海域海表面风的统计降尺度模型，并利用2008—2011年的观测数据对降尺度模型进行了预报检验。获得以下几点认知：

（1）CCMP风场风速（W）的前15个空间模态和NCEP-DOE（W，SLP，SST）变量的前20个空间模态，分别占各自总方差贡献的95.6%和97.3%，基本涵盖了CCMP风场风速及NCEP-DOE海表面风速、气压、温度等变量的绝大部分信息；

（2）利用CCMP（W）与NECP-DOE（W，SLP，SST）两者典型空间模态的长期统计关系，能够较为合理地构建出适合于我国海域的海表面风统计降尺度模型。模型交叉验证结果证实：模拟与观测两者风速空间分布的相关性R值可达0.98以上，风速变化趋势的相关性R值可达0.89（预测模拟）和0.93（回算模拟）；

（3）在陆域沿岸的近海区，统计降尺度模型的模拟能力相对较弱，预测风速的RMSE、AE及RE的大值区多发生在陆域近海，但模型的总体预测误差相对较小，绝大多数海域的RMSE值和AE值均低于0.25 m/s和0.30 m/s，RE＜-5%或RE＞5%的海区面积仅约占全海域的5%左右。

本文仅以NCEP-DOE（W，SLP，SST）作为预测因子，以CCMP（W）作目标变量，构建了我国海域海表面风的统计降尺度模型，意在能为区域海表面风的降尺度研究提供一些相关参考。如果用全球环流模式（GCM）预估数据替代NCEP-DOE数据，以其作为统计降尺度模型的预测因子，那么便可开展我国海表风未来情景变化的降尺度分析，这方面研究将是我们下一步需开展的工作。

［1］范泽孟，岳天祥，陈传法，等.中国降水未来情景的降尺度模拟［J］.地理研究，2012，31（12）:2283-2291.

［2］陈威霖，江志红，黄强.基于统计降尺度模型的江淮流域极端气候的模拟与预估［J］.大气科学学报，2012，35（5）:578-590.

［3］成爱芳，冯起，张健恺，等.未来气候情景下气候变化响应过程研究综述［J］.地理科学，2015，35（1）:84-90.

［4］朱宏伟，杨森，赵旭喆，等.区域气候变化统计降尺度研究进展［J］.生态学报，2011，31（9）:2602-2609.

［5］陈华，郭家力，郭生练，等.统计降尺度方法及其评价指标比较研究［J］.水利学报，2012，43（8）:891-897.

［6］Sailor D J，Li X S.A semiempirical downscaling approach for predicting regional temperature impacts associated with climatic change［J］.Journal of Climate，1999，12（1）:103-114.

［7］Murphy J.Predictions of climate change over Europe using statistical and dynamical downscaling techniques［J］.International Journal of Climatology，2000，20（5）:489-501.

［8］Mpelasoka F S，Mullan A B，Heerdegen R G.New Zealand climate change information derived by multivariate statistical and artificial neuralnetworksapproaches［J］.InternationalJournalof Climatology，2001，21（11）:1415-1433.

［9］Bárdossy A，Stehlík J，Caspary H J.Automated objective classificationofdailycirculationpatternsforprecipitationand temperature downscaling based on optimized fuzzy rules［J］. Climate Research，2002，23:11-22.

［10］Goodess C M，Hall J，Best M，et al.Climate scenarios and decision making under uncertainty［J］.Built Environment，2007， 33（1）:10-30.

［11］范丽军.统计降尺度方法集合预估华东气温的初步研究［J］.高原气象，2010，29（2）:392-402.

［12］崔妍，江志红，陈威霖.典型相关分析方法对21世纪江淮流域极端降水的预估试验［J］.气候变化研究进展，2010，6（6）:405-410.

［13］薛春芳，董文杰，毛明策，等.渭河流域秋雨统计降尺度预估的试验研究［J］.热带气象学报，2013，29（5）:849-856.

［14］Guo Y，Li J P，Li Y.Seasonal forecasting of North China summer rainfall using a statistical downscaling model［J］.Journal of Applied Meteorology and Climatology，2014，53（6）:1739-1749.

［15］阮成卿，李建平，冯娟.中国西南地区后冬降水的统计降尺度模型［J］.中国科学:地球科学，2015，45（7）:1020-1033.

［16］汤剑平，高红霞，李艳，等.IPCC-A2情景下我国21世纪风能变化的统计降尺度方法研究［J］.太阳能学报，2009，30（5）: 655-666.

［17］Atlas R，Hoffman R N，Ardizzone J，et al.A cross-calibrated，multiplatformoceansurfacewindvelocityproductfor meteorological and oceanographic applications［J］.Bulletin of the American Meteorological Society，2011，92（2）:157-174.

［18］赵天保，符淙斌，柯宗建，等.全球大气再分析资料的研究现状与进展［J］.地球科学进展，2010，25（3）:242-254.

［19］姚志刚.全球气候变化对美国东海岸区域气候变化和风暴潮活动影响的研究［D］.青岛:中国海洋大学，2012:13-24.

［20］孙龙，于华明，王朋，等.东中国海及毗邻海域海面风场季节及年际变化特征分析［J］.海洋预报，2010，27（2）:30-37.

［21］王慧，隋伟辉.基于CCMP风场的中国近海18个海区海面大风季节变化特征分析［J］.气象科技，2013，41（4）:720-725.

［22］Fu G，Zhang S P，Gao S H，et al.Understanding of sea fog over the China seas［M］.Beijing:China Meteorological Press，2011: 91-127.

［23］齐义泉，施平，王静.卫星遥感海面风场的进展［J］.遥感技术与应用，1998，13（1）:56-61.

［24］袁俊鹏，江静.西北太平洋热带气旋路径及其与海温的关系［J］.热带气象学报，2009，25（S1）:69-78.

［25］Hoffman R N，Ardizzone J V，Leidner S M，et al.Error estimates for ocean surface winds:applying desroziers diagnostics to the cross-calibrated，multi-platform analysis of wind speed［J］.Journal of Atmospheric and Oceanic Technology，2013，30（11）:2596-2603.

Studies of statistical downscaling model of sea surface wind over China seas

LI Zheng-quan，XIAO Jing-jing，MAHao，FENG Tao
（Zhejiang Climate Center，Hangzhou 310017 China）

Based on long-term statistical relationship of typical spatial modes derived from CCMP wind data and NCEP-DOE reanalysis data，a statistical downscaling model of sea surface wind over China seas is constructed. The results of cross-validation indicate that the simulated wind speed agrees well with the wind speed from CCMP observation，both in spatial pattern and in annual variation.The correlation coefficient（R）of model simulating and CCMP observation is above 0.98 for wind speed spatial pattern，and higher than 0.89 for wind speed annual variation.Moreover，simulating errors of the statistical downscaling model are very low.In most of sea areas，RMSE of wind speed is lower than 0.25 m/s and AE is lower than 0.30 m/s.Only in about 5%sea areas，its RE is higher than 5%or lower than-5%.The errors spatial patterns show that large errors often occur in some offshore areas，because the offshore winds are affected by many factors that come from active local weather systems in meso-scale and small-scale.

sea surface wind；statistic downscaling；empirical orthogonal function；CCMP wind field；NCEPDOE

P732

A

1003-0239（2016）04-0071-09

10.11737/j.issn.1003-0239.2016.04.009

2015-10-16

中国气象局气候变化专项（CCSF201427）；浙江省气象科技计划重点项目（2014ZD05）；公益性行业（气象）科研专项（GYHY201306050）。

李正泉（1978-），男，高级工程师，博士，主要从事气候变化与生态研究。E-mail∶lzq110119@163.com