水平轴潮流能水轮机数值模拟方法对比分析
2016-10-25王兵振段云琪
廖 微,王兵振,张 巍,段云琪
(国家海洋技术中心,天津 300112)
水平轴潮流能水轮机数值模拟方法对比分析
廖微,王兵振,张巍,段云琪
(国家海洋技术中心,天津300112)
叶素动量理论和CFD方法是水平轴潮流能水轮机性能分析中运用较为广泛的数值模拟方法,文中结合小尺寸水轮机模型试验,对比分析了叶素动量理论和CFD方法在水轮机性能分析中的准确性和适用性。验证结果表明:叶素动量理论和CFD方法均能对水轮机的性能进行预报,且CFD精度高于动量叶素理论;大尖速比时,动量叶素理论偏离较高,不再适合性能预报;在小尖速比下,建议采用RNG k-ε模型的CFD方法进行分析计算;动量叶素理论适合设计初期设计方案的对比分析,而CFD方法适合对设计结果的验证校核和详细分析。
水平轴水轮机;数值模拟;叶素动量理论;CFD方法;水池试验
随着经济发展与能源短缺、环境污染等矛盾的日益突出,潮流能作为一种能量密度高、储备能量大、可再生的清洁能源受到各国政府青睐。据统计,我国的潮流能储量达到13 948.5 MW[1],是世界上潮流资源较为丰富的国家之一,潮流能发电技术在我国有较好的应用前景。
水轮机是潮流能系统中能量转换的核心构件,对水轮机性能的准确预报是水轮机设计的关键。叶素动量理论和CFD方法是水轮机水动力分析中运用最为广泛的两种方法。Bahaj[2]等采用叶素动量理论对水平轴水轮机进行数值模拟及试验验证;王树杰[3]等采用CFD对水轮机进行数值模拟,对比分析了不同湍流模型的应用;Ju Hyun[4]等将CFD计算结果与试验值、VLM方法、BEM方法进行了比较;盛其虎[5]等总结了潮流能水轮机水动力分析的常用方法。本文结合小尺寸水轮机模型试验,对比分析了叶素动量理论和CFD方法在水轮机性能分析上的准确性和适用性。
1 水轮机模型
本文进行分析验证的水平轴潮流能水轮机模型的直径为0.8 m,水轮机叶片翼型采用NACA63-424,设计尖速比为6,理论最佳功率系数为0.4,叶片数为2。叶片的设计结果如图1所示。

图1 模型叶片设计结果
2 叶素动量理论
叶素动量理论是水轮机设计与性能分析中应用最为广泛的方法,它结合叶素理论和动量理论,将叶片沿翼展方向分割为若干个叶素,并假定相邻叶素间没有干扰,叶素上的流动为二维流动,因此每个叶素所受的力与力矩只与该处叶素剖面翼型升阻力相关,受力大小可采用叶素扫略圆环时发生的流体动量变化进行计算。
采用叶素动量理论对水轮机性能进行计算是一个对叶素处流体流动的轴向诱导系数和周向诱导系数不断迭代求解的过程。单个叶素的流体速度和受力情况如图2所示。假定叶素位于半径为r的位置,叶素径向宽度为dr。根据叶素动量理论以及Prandtl修正[6],该叶素处流体流动的轴向诱导速度和周向诱导速度为:
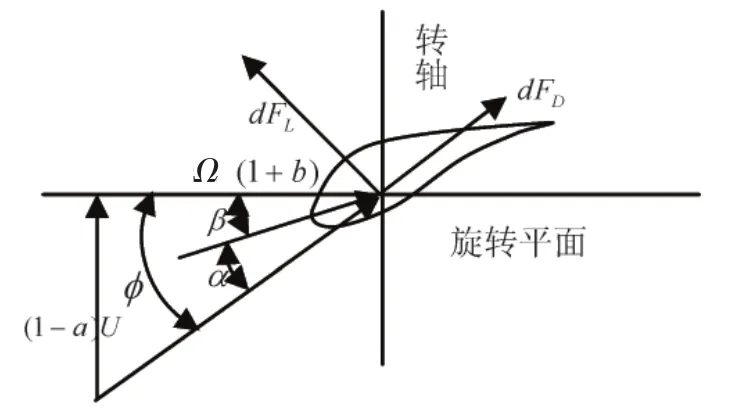
图2 叶素流体速度分布和受力示意图
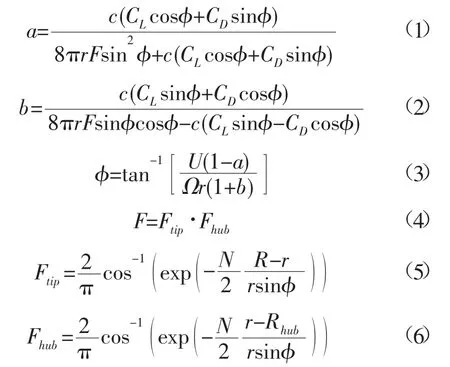
式中:a为轴向诱导系数;b为周向诱导系数;Ω为叶轮旋转角速度;U为无穷远处来流速度。CL,CD分别为叶素翼形的升力和阻力系数;c为叶素的弦长;Ftip为叶尖损失系数;Fhub为轮毂损失系数;Rhub为轮毂半径;N为叶片数;φ为水流速度和叶轮旋转平面之间的角度即叶素入流角。
当轴向诱导系数大于0.5时,叶轮工作在湍流状态,动量理论不再适用,需要对a进行修正。本文采用文献[7]提出的方法,通过推力系数CT的经验公式对a进行修正:

当求解得a,b后,即可求得叶素所受力、力矩与功率系数,对所有叶素所求量进行积分即可求解整个叶轮的受力与功率系数。
3 CFD方法
随着计算机硬件水平的提高和计算流体力学的发展(CFD),采用基于 FLuent,CFX[8],STAR CCM+[9]等商业软件的CFD方法得到了广泛运用。根据水轮机的工作环境,CFD求解模式通常为雷诺时均的不可压缩粘性流体的定常流动,并引入湍流模型对流体运动方程组进行封闭求解。其中,在对潮流能水轮机的性能分析中,运用最为广泛的为k-ωSST湍流模型和RNG k-ε湍流模型。k-ωSST湍流模型被证明与试验值具有较好的吻合度[9-10],其结合了标准k-ω湍流模型和标准k-ε湍流模型的优势,在处理近壁面时,采用标准k-ω湍流模型,在边界层边缘和自由剪切层时,采用k-ε湍流模型,从而提高了计算的准确性[3]。RNG k-ε由于考虑了平均流动中的旋流,能更好地处理高应变率和流线弯曲较大的流动。为对两种常用湍流模型在水轮机水动力数值模拟中的准确性进行比较,本文在相同计算模型、计算网格和参数设置下,分别采用k-ωSST湍流模型和RNG k-ε湍流模型进行数值模拟计算,并将计算结果与水槽试验结果进行对比分析。
利用Ansys建立设计0.8 m直径潮流能叶轮的水动力计算模型,如图3所示,计算域划分为旋转域和静止域,旋转域为包裹叶轮及其周围的圆柱形区域,静止域为距上游3D、下游6D、半径2.5D的圆柱形区域,以使叶轮处尾流充分发展并尽量减小流域壁面效应。在Fluent中,采用多参考坐标系模型(MRF)进行求解。

图3 叶轮计算域

图4 叶轮网格示意图
网格质量和边界条件的选择对计算结果具有很大的影响。利用网格划分工具ICEM CFD进行网格划分,对旋转域采用四面体非结构网格,并在叶轮壁面附近进行网格加密以保证叶轮壁面Y+值处于合适的范围;对静止域采用六面体结构网格划分以减小网格数量,加快收敛速度和计算精度。图4为网格示意图,其中旋转域网格单元数为163.4万,静止域网格单元数为18.8万,计算总单元数为182.2万左右。在边界条件的设置上,设置入口流体速度为恒值速度,采用湍流强度值和水利直径定义湍流参数,设置出口边界条件为自由流出口或压力出口边界,叶轮壁面设置为无滑移壁面边界条件。
4 模型试验与结果分析
4.1模型水池试验
利用CFD中的k-ωSST湍流模型和RNG k-ε湍流模型以及叶素动量理论对设计0.8 m直径叶轮进行数值模拟计算,并与模型试验结果进行了对比,从而从计算准确性和适用性两方面对CFD数值模拟方法和叶素动量理论方法进行对比,并分析两种数值模拟方法的适用范围。
为验证叶素动量理论和CFD方法对水轮机性能分析的准确性,本文对上述水平轴潮流能水轮机模型在天津大学船舶拖曳水池进行了叶轮动力特性测试试验。水池长140 m,宽7 m,水深3 m,试验装置主要由叶轮、传动装置、转速/扭矩传感器、发电机、控制电路等部分组成,如图5所示。在试验过程中将模型固定在拖车上,利用拖车拖动模型在水中运动,保持拖车拖曳速度为2.0 m/s,通过改变转轴输出端的负载改变叶轮旋转速度,以将转速控制在230±10 rpm,250±10 rpm,280±10 rpm,300±10 rpm,350±10 rpm,400±10 rpm附近,并通过转速扭矩传感器测得输出转速、转矩值,从而获得不同尖速比下的转速、转矩值。
由于扭矩传感器安装在传动系统的后端,因此,测量的扭矩数值受传动系统的摩擦损失的影响,其数值会略小于叶轮输出的扭矩值。为准确地考察叶轮的输出扭矩,减小传动系统摩擦损失影响,设计了传动系统摩擦损失测量装置对传动系统的摩擦阻力矩进行了测量。
利用测量的数据计算不同尖速比下叶轮的功率系数。叶轮的功率系数按下式估算:

式中:Cp为叶轮的功率系数,即能量转换效率;Po为拖曳试验时扭矩传感器输出的机械功率与传动系统摩擦力矩产生的损失功率之和;Pi为水对叶轮作用所产生的输入功率,按式(9)估算:

式中:ρ为水的密度;v为模型相对水的运动速度;S为叶轮扫略面积。

图5 试验装置
4.2结果分析
4.2.1准确性为比较分析CFD方法和BEM方法在水平轴水轮机数值中的准确性,本文首先对水轮机的CFD分析中最常用的两种湍流模型k-ωSST模型和RNG k-ε模型进行分析对比以确定适合的湍流模型,再将确定后的湍流模型计算结果与BEM方法进行对比分析,验证两种数值计算方法的计算准确性。在对水轮机进行数值模拟计算时,为保证计算结果的可对比性,数值模拟计算采用的速度和尖速比值均与水槽试验值保持一致。
在CFD分析中,为保证结果的可对比性,除湍流模型及对应参数存在差异外,两种湍流计算中的计算模型、网格划分、参数设置等均保持一致。计算结果和试验结果对比如图6所示,两种湍流模式对水平轴水轮机性能的预测均具有一定的准确性。在最优设计尖速比附近,两者与实验值的误差均在1%以下,且k-ωSST模型计算精度较RNG k-ε模型稍高;在小尖速比下,RNG k-ε湍流模型计算结果较k-ωSST模型更吻合实验值,但两种的计算误差均随着尖速比的减小而增大,在TSR=4.77时,两者误差分别为4.9%和11.5%;当尖速比大于最优设计尖速比,k-ωSST和RNG k-ε的计算结果变化趋势相同,且均在最大尖速比8.69下达到最大误差,分别为11.3%和10.2%。整体上,在各尖速比下RNG计算值均小于SST计算值;SST湍流模型的整体精度高于RNG模型,但在小尖速比下精度低于RNG湍流模型。在下述与BEM计算方法的对比中,在小尖速比下采用RNG计算值、其他尖速比下采用SST计算值作为CFD计算值进行对比分析。
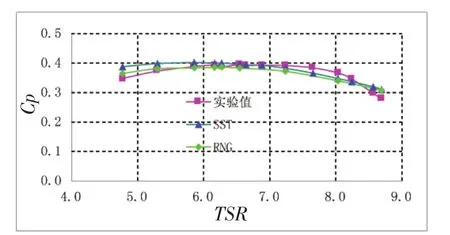
图6 RNG和SST计算值比较
图7为BEM数值模拟方法与CFD数值模拟方法计算结果值与实验值的对比。如图所示,两种数值模拟方法与试验结果吻合,在设计尖速比附近计算精度最高。BEM、CFD、试验测量的最佳尖速比均在0.65附近,其对应的的最佳功率系数分别为0.415 9,0.396 6,0.395 9,BEM,CFD方法对最佳功率系数的预报误差分别为5.04%和0.15%。在偏离设计尖速比时,两种计算方法的误差均增大:随着尖速比减小,CFD计算误差逐渐大于BEM计算误差;随着尖速比增大,BEM计算逐渐偏离试验值且偏差较大。

图7 试验值与数值模拟值的比较
随着尖速比偏离最佳尖速比,采用CFD计算得到的误差均增大,其原因可能是:(1)试验环境和CFD数值模拟环境的差异,如雷诺数、湍流强度等;(2)CFD计算方法本身的计算误差:能较好地计算压差阻力,但对粘性摩擦阻力的计算准确性偏低;(3)试验本身的误差,如壁面效应、自由表面的影响等。4.2.2适用性在本文中,叶素动量理论算法的实现基于Matlab编程,单一工况的计算CPU时间在1 s左右,采用叶素动量理论的时间成本主要集中在对叶素动量理论的MATLAB编程上,对所有工况计算的CPU时间在10 s内。采用模块化编程,可方便地对包括设计尖速比、叶片直径、叶片数等叶片外形参数和计算参数等进行更改计算。且编程计算对计算机资源要求较低,内存占据少。CFD计算过程涉及三维建模、网格划分、Fluent计算,时间成本主要集中在后两步。网格划分所需时间依赖于网格类型的选择、网格精度、个人操作熟练度等,需要较多的时间和精力;在Fluent计算过程上,采用8核CPU、内存3.43G的计算机做8核并行计算单一工况所需时间为2 h左右。一旦叶片外形参数发生改变,则需重新进行三维建模以及后续过程,若只更改计算工况,则只需在Fluent中更改参数进行计算。
在潮流能水轮机设计初期,需要进行大量运算对不同设计方案进行计算对比,确定最佳叶片数、设计尖速比等设计参数。若采用CFD方法,则需对每一个方案重复建模、网格划分、Fluent分析过程,需要耗费大量的时间,采用叶素动量理论,可以在保证一定精度的基础上节省时间。初步设计方案确定后,需要对单一设计结果进行多工况的计算验证和详细分析,获取包括流场分布、尾流反作用等详细信息,而这些信息无法从叶素动量理论中计算获得,需采用更复杂、精度更高的CFD方法。
5 结论
本文结合小尺寸水轮机模型试验,对比分析了叶素动量理论、CFD方法在水平轴水轮机性能分析中的准确性和适用性,结果说明:
(1)采用叶素动量理论和CFD方法均能较为准确地分析水轮机的性能,且CFD的计算精度要高于叶素动量理论的计算精度。
(2)在最佳尖速比附近,两种数值方法计算精度最高;在小尖速比下,叶素动量理论的计算精度高于k-ωSST模型的精度,但低于RNG k-ε模型,建议采用RNG k-ε模型的CFD方法进行计算;在大尖速比下,BEM计算结果与试验偏差较大。
(3)BEM方法计算成本低、精度适中,适合水轮机设计初期对性能的分析;CFD计算成本高,计算精度较高,结果详细,适合设计后期对设计方案的验证分析。
[1]戴庆忠.潮流能发电及潮流能发电装置[J].东方电机,2010(2):51-66.
[2]ASBahaj,WGJ Batten,GMcCann.Experimental Verification ofNumerical Predictions for the Hydrodynamic Performance ofHorizontal Axis Marine Current Turbine[J].Renewable Energy,2007(32):2479-2490.
[3]王树杰,盛传明,袁鹏,等.潮流能水平轴水轮机湍流模型研究初探[J].中国海洋大学学报,2014,44(5):95-100.
[4]Ju Hyun Lee,SunhoPark,DongHwan Kim,et al.Computational methods for performance analysis ofhorizontal axis tidal stream turbines[J].Applied Energy,2012,98:512-523.
[5]盛其虎,孙科,张学伟,等.潮流能水轮机水动力分析方法[J].海洋技术学报,2014,33(4):105-111.
[6]Prandtl L,Tietjens O K G.Applied Hydroand Aeromechanics,based on Lectures ofI.Prandtl,PhD[M].Mineola:Dovel Publications.com,1957.
[7]Ju Hyun Lee,Dong Hwan Kim,Shin Hyung Rhee,et al.Comptuational and Experimental Analysis for Horizontal Axis Marine Current Turbine Design[C]//Second International Symposiumon Marine Propulsorsamp’ll.Hamburg,Gemany,2011.
[8]盛其虎,赵亚东,张亮.水平轴潮流能水轮机设计与数值模拟[J].哈尔滨工程大学学报,2014,35(4):389-394.
[9]MJ Lawson,YLi,D C Sale.Development and Verification ofa Computational Fluid Dynamics Model ofa Horizontal-Axis Tidal Current Turbine[R].Netherlands,2011.
[10]Pape A,Lecanu J.3DNavier-Stokes Computations ofa Stall-regulated Wind Turbine[J].Wind Energy,2004,7(4):309-324.
Comparative Analysis on the Numerical Simulation Methods for Horizontal Axis Tidal Current Turbines
LIAO Wei,WANG Bing-zhen,ZHANG Wei,DUAN Yun-qi
National Ocean Technology Center,Tianjin 300112,China
This paper conducts a comparative analysis on the accuracy and applicability of the blade element momentum(BEM)theory and computational fluid dynamics(CFD)method,the two most widely used numerical simulation methods for hydrodynamic performance analysis of horizontal axis tidal current turbine.To verify the computational results,an open water test is carried out in a towing tank with a self-designed turbine.The results show that both the two methods can provide a satisfactory prediction for the experimental turbine performance,and a higher accuracy is acquired with CFD.With increasing tip speed ratio(TSR),higher deviation is observed with the BEM theory,not applicable for prediction anymore.For low TSR,in contrast,it is suggested that the CFD method of the RNG model be adopted for analysis and calculation.Furthermore,the use of BEM is suited to the comparative analysis of the design scheme under early stage,while CFD is for post-design validation and indepth analysis.
horizontal axis tidal current turbine;numerical simulation;blade element momentum theory;computational fluid dynamic(CFD)method;towing tank test
P743
A
1003-2029(2016)01-0113-05
10.3969/j.issn.1003-2029.2016.01.018
2015-03-14
海洋公益性行业科研专项经费资助项目(201205019-3)
廖微(1990-),在读硕士,主要研究方向为港口、海岸与近海工程。E-mail:lanmengxinfei555@163.com
