变幅载荷对高温合金裂纹萌生及扩展寿命的影响

初金阳，申秀丽，毛建兴，胡殿印，王荣桥

（1.北京航空航天大学能源与动力工程学院，北京100191；2.先进航空发动机协同创新中心，北京100191；3.中航工业商用发动机有限责任公司，上海200241）

变幅载荷对高温合金裂纹萌生及扩展寿命的影响

初金阳1，3，申秀丽1，2，毛建兴1，胡殿印1，2，王荣桥1，2

（1.北京航空航天大学能源与动力工程学院，北京100191；2.先进航空发动机协同创新中心，北京100191；3.中航工业商用发动机有限责任公司，上海200241）

为了更好地分析航空发动机用高温合金裂纹萌生阶段的变幅载荷对高温材料的低周疲劳裂纹萌生及扩展寿命的影响，将低周疲劳的裂纹萌生过程视作损伤累积过程，基于连续损伤力学建立了低周疲劳损伤累积模型。结合室温下G Q G H 4169合金的裂纹扩展试验数据，通过有限元建模计算和数值分析方法确定了模型中具体的损伤参数数值，并对裂纹萌生寿命进行了预测。结果表明：该方法不但能准确地预测变幅加载下CT试样的裂纹萌生寿命，而且能很好地反映萌生阶段变幅载荷对裂纹扩展寿命的影响，而且降低了试验成本。

变幅载荷；裂纹萌生；裂纹扩展；连续损伤力学；高温合金；低周疲劳；航空发动机

0　引言

低周疲劳一直是航空航天领域的一大难题，其主要表现形式为长裂纹扩展引起的结构件断裂。材料的疲劳寿命一般由裂纹的萌生寿命和裂纹扩展寿命组成［1］。对于航空发动机等受力情况复杂的构件，裂纹在萌生及扩展阶段都受到变幅载荷的影响。通过试验可知，不同受力情况下萌生的裂纹在扩展阶段的扩展速率差异明显，影响材料的整体低周疲劳寿命。因此，分析裂纹萌生阶段变幅载荷对裂纹萌生寿命及扩展寿命的影响是非常有必要的。

目前大量使用的高温合金主要是铁基、镍基和钴基高温合金［2-3］。由于GH4169合金在650℃以下有塑性好、屈服强度高、高温抗氧化性好、耐腐蚀性强等优点，在航空发动机中主要用于制作涡轮盘、叶片、耐高温紧固件等关键结构部件［4］。而GQGH4169合金是目前中国应用较为广泛的高温高强度航空类合金，以该材料为例研究变幅载荷对低周疲劳寿命的影响。

目前，求解裂纹萌生寿命广泛应用的是Manson［5］与Coffin［6］各自独立提出的材料疲劳寿命的经验关系式，即Manson-Coffin方程。该方程揭示了塑性应变幅和疲劳寿命之间的经验关系。求解裂纹扩展寿命广泛应用的是Paris定律［7］，该定律揭示了裂纹扩展速率与应力强度因子之间的关系。Manson-Coffin方程和Paris定律虽然能分别准确地预测裂纹萌生寿命和裂纹扩展寿命，但不能很好地反映变幅载荷对2种寿命的影响。

本文基于连续损伤力学，建立了低周疲劳损伤累积模型。结合试验数据，采用Paris公式进行拟合，利用裂纹闭合效应和损伤原理分析了裂纹萌生阶段的变幅载荷对裂纹在扩展阶段的影响。

1　材料和试验

1.1材料和试样

试样采用的GQGH4169合金在室温时的基本力学参数［8］见表1。

表1　GH4169合金的力学参数

裂纹扩展试样取自涡轮盘锻件，弦向取样。采用标准紧凑拉伸（Compact Tension，CT）试样，具体尺寸如图1所示。

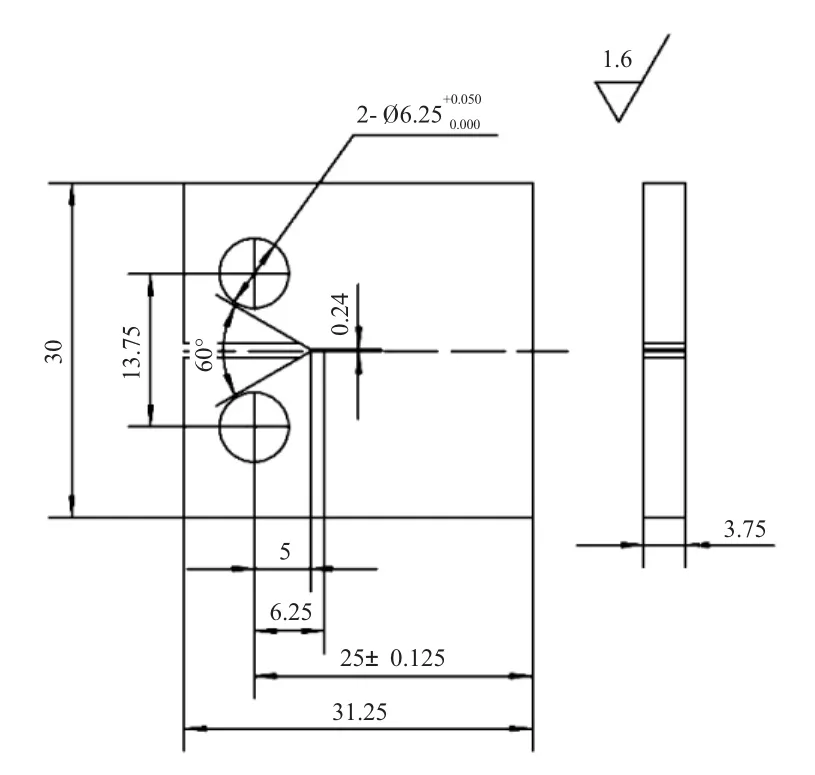
图1　CT试样尺寸

1.2试验方案

试验在SDS100型电液伺服疲劳机上进行，采用电子显微镜进行实时观察，通过数显表记录裂纹的实时长度。按照GB/T6398—2000《金属材料疲劳裂纹扩展速率试验方法》的要求进行试验。为了准确分析变幅载荷对试样疲劳寿命的影响，采用了控制变量法。试验温度为室温20℃，采用三角波加载，频率f=10 Hz，应力比R= 0.1，通过改变最大加载载荷进行试验。试验分为2步：第1步预制裂纹扩展到0.2 mm左右，第2步加载至试件断裂，加载情况见表2。

表2中5、6试验组为变幅载荷预制疲劳裂纹，每个载荷的加载周期为300 cycles。

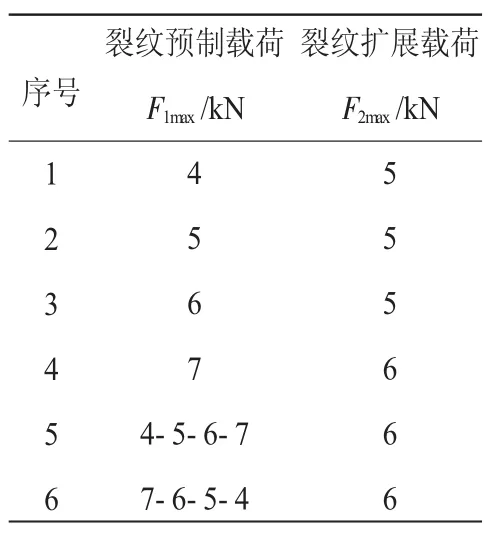
表2　CT试样加载数据

2　低周疲劳损伤累积模型

2.1连续损伤力学基本原理

根据热力学定义：在等温过程中，封闭系统对外作功等于或小于系统Helmholtz自由能的减少。故对于等温无穷小变形（无热量交换）过程，Clausius-Duhamel不等式可表示为

式中：σij为Cauchy应力张量；为无穷小应变张量；为Helmholtz自由能密度的变化率［9］。

假设材料损伤过程中是弹性且各向同性的，则Helmholtz自由能可看作应变能。标量损伤变量可定义为

式中：E为材料的弹性模量；E'为损伤后的弹性模量。忽略其它变量只用损伤变量D和应变张量εij来描述损伤状态时，Helmholtz自由能密度表示为

式中：2个内变量σij和Y分别为εij和D的对偶变量。

根据内变量的正交流动法则［9］，Lemaitre提出损伤演化方程［10］为

其中Helmholtz自由能密度对D的释放率Y定义为

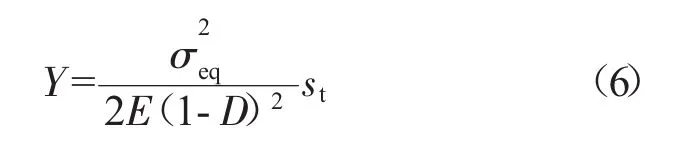
3轴因子st表示为

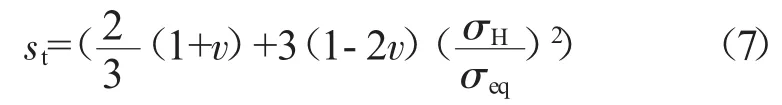
式中：σH为静水压力；σeq为Von Mises等效应力；v为泊松比。

2.2损伤模型的建立

Miner准则描述的线性损伤累积原理被广泛应用。认为在相同受力情况下，损伤变量D与加载循环数成正比

但它并不能反映变载荷情况下加载次序对材料疲劳寿命的影响，且预测精度较低。

各向同性材料的耗散势可以表示为［11］

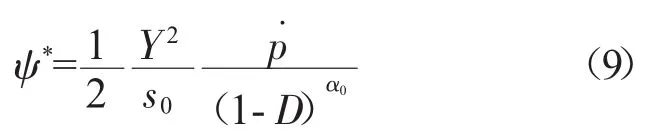
联立式（5）、（6）和（9）可以得到非线性损伤演化方程

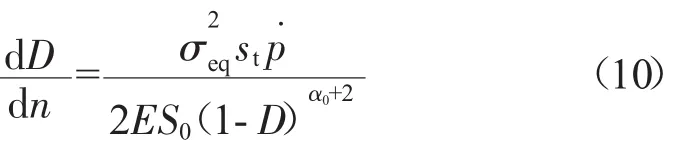
材料受到循环载荷时，往往会发生循环硬化或循环软化。对于低周疲劳，连续损伤力学中将累积塑性变形看作损伤形成的主要原因。随着累积塑性变形的增大会产生循环软化，并影响其变化率。因此，可以把材料的循化软化看作疲劳损伤过程［12］。稳定的循环软化过程采用通用金属循环应力-应变关系来描述

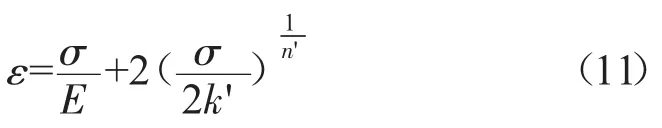
式中：k'为循环强度系数，n'为循环硬化指数；等号右半部分别为循环软化稳定时每循环的弹性应变和塑性应变，塑性应变对应力求导可以得到

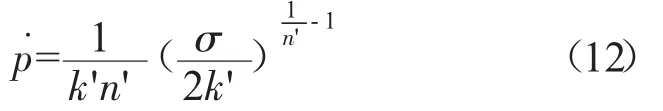
假设循环为比例加载，且每个循环过程中损伤程度不变，可以通过对式（10）进行积分得到损伤累积模型。根据D的定义可知，材料无损伤时，D=0，裂纹萌生时，D=1［13］。由弹性模量定义可知其在材料损伤过程中不断减小，为了简化计算，采取有效应力法，即假设损伤过程中弹性模量不变，用损伤等效应力来描述损伤处的受力状态。无损伤时，单轴受载下材料局部所受应力σ=σeq。根据式（6）、（9），裂纹萌生处的受力状态可以用损伤等效应力表示：，即。

对于GH4169合金，从开始加载到稳定循环软化阶段，通常为十几至几十个循环［12］。忽略此阶段，裂纹萌生过程可以近似看作稳定循环软化过程，可得到材料低周裂纹萌生寿命方程为

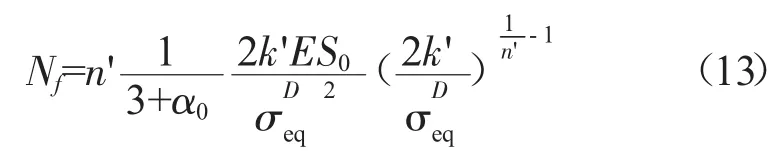
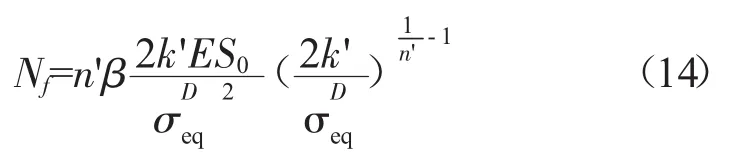
3　变幅载荷对疲劳寿命的影响

3.1有限元建模及分析

根据文献［14］，当GH4169合金的裂纹尺寸达到0.2 mm后，扩展速率明显提升，将0.2 mm定为裂纹萌生尺寸。GQGH4169合金在常温下力学性能与GH4169合金的十分相近。通过试验看出：裂纹扩展速率首次明显提升也是在0.2 mm左右，可认为此时的循环数为裂纹萌生寿命。进而通过有限元方法分析CT试样裂纹萌生处的局部载荷。采用有限元软件ANSYS用平面单元Solid182建模并计算，网格结果如图2、3所示。

对裂纹萌生处进行了局部网格细化：对模型的右半底边施加对称约束；将圆孔上半圆弧的节点进行Y方向耦合；在顶点施加Y方向载荷并对其进行X轴约束。试验结果及有限元计算结果见表3。

图2　CT试样网格划分

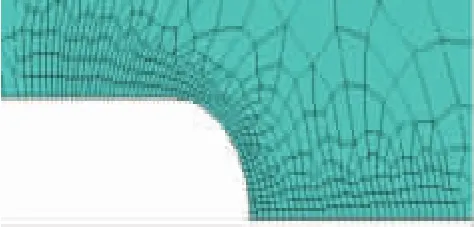
图3　裂纹萌生处网格细分

表3　不同受力状态的裂纹萌生寿命

3.2变幅载荷对裂纹萌生的影响

由前文所述，等幅加载下的裂纹萌生寿命可通过式（14）求出。但对于GQGH4169合金，方程中的损伤参数尚无法确定，损伤强度是材料常数，β可看作是最大损伤等效应力的幂函数［15］。结合试验数据进行拟合可以确定未知参数。

根据式（10）可知材料损伤程度为D时对应的加载循环数为

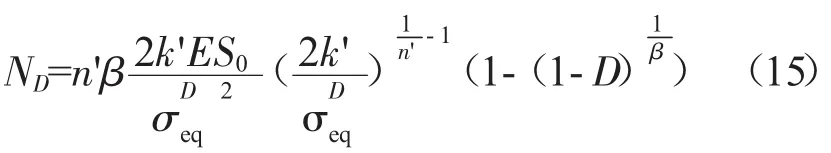
将上式与式（14）相除可得

假设加载过程中每次循环的损伤为Di，则有

当材料承受多级载荷时，应把之前加载受到的损伤进行累计。因此，在承受第i级载荷时造成的损伤变量可以定义

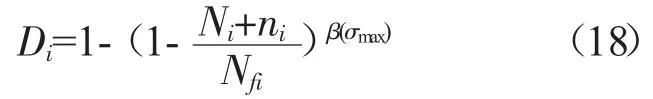
式中：Ni和ni分别为第i-1级载荷造成的累积损伤转化为第i级载荷时对应的循环数和第i级载荷加载下的循环数。

将之前的累积损伤转化为第i级载荷加载下造成的损伤即

引入中间变量

县域电力通信网规划与建设受经济发展水平、负荷发展水平、网络建设和业务需求等多种因素影响。县域电力通信网的建设应遵循“统筹规划、适度超前、技术合理、因地制宜、安全可靠、经济高效”的原则。对于中国而言，发展县域电力通信网，可以有效提高农网供电可靠性，促进农网智能化。

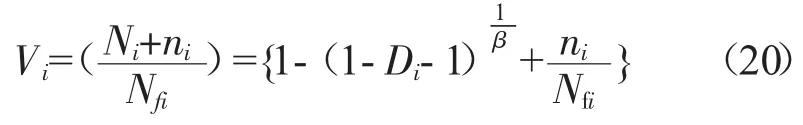
式（19）可以表示为

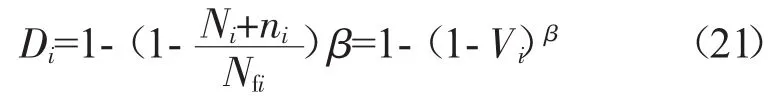
结合表3中的等幅加载数据和任1组变幅加载数据，可以通过MATLAB进行拟合得出式（14）中未知参数的数值，进而对另1组变幅加载条件下的萌生寿命进行预测。拟合结果：损伤强度的数值为1.05e-3，等幅加载对应的β值见表4。

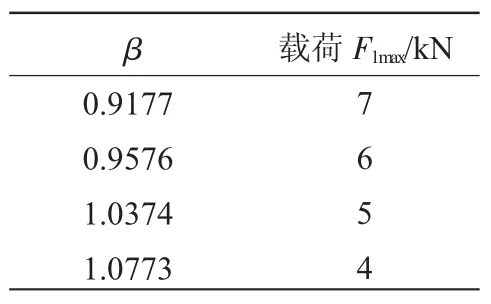
表4　不同受力状态下的β值

因此，在不同受力状态下的裂纹萌生寿命可以通过以上确定的参数代入损伤模型中进行预估，降低了试验成本。变幅载荷的裂纹萌生寿命预测结果见表5。

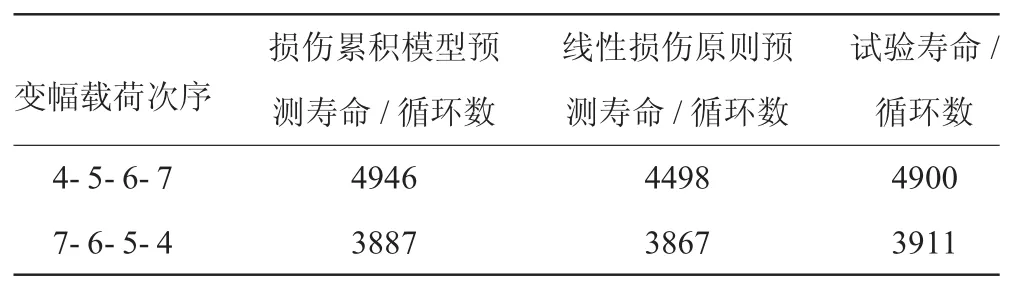
表5　变幅载荷下裂纹萌生寿命预测结果

从表中可见，非线性损伤累积模型不但能反映变载荷情况下加载次序对萌生寿命的影响，而且相对线性损伤原则对变幅加载的裂纹萌生寿命的预测精度更高。

3.3变幅载荷对裂纹扩展的影响

求解裂纹扩展寿命，常选用Paris公式

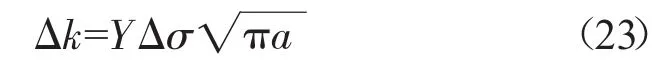
式中：Y为形状修正因子，与裂纹的结构形式有关。

裂纹尖端扩展速率表示为

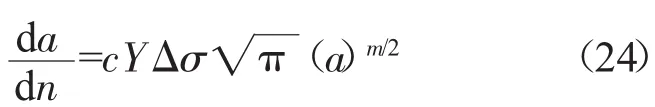
简化为

从式（25）中可见，等幅加载的裂纹扩展寿命是a的指数函数。裂纹扩展阶段最大载荷为5、6 kN时的拟合结果如图4、5所示。图中各试样在裂纹萌生阶段又都承受不同的最大载荷F1max。

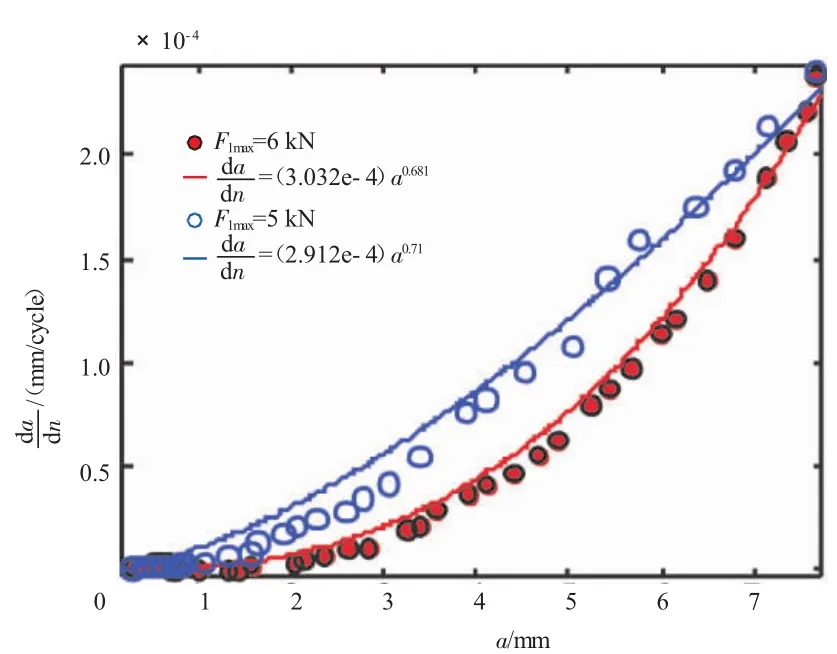
图4　最大扩展载荷为5 kN的拟合曲线结果

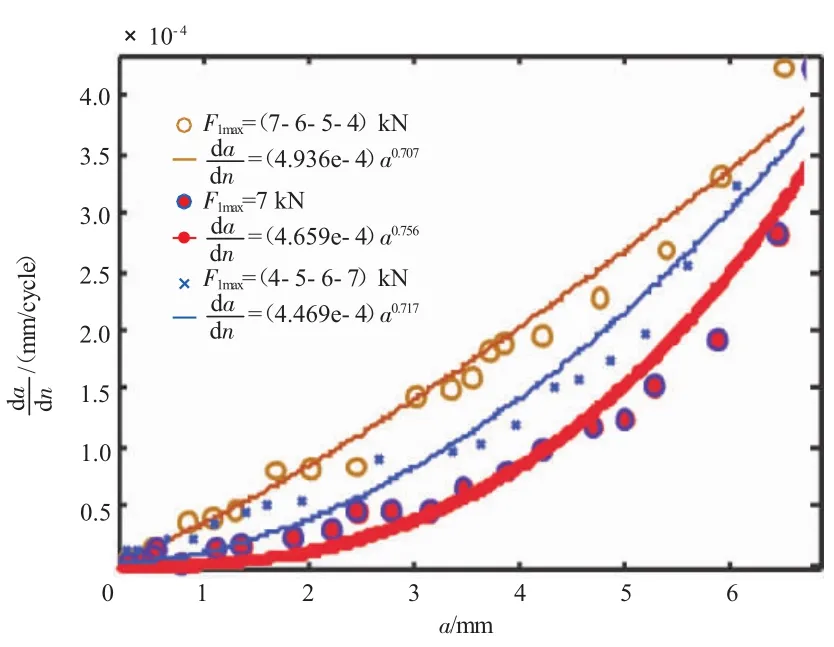
图5　最大扩展载荷为6 kN的拟合曲线结果

从图中可见，相对于等幅加载，变幅加载的图像都有明显转折。该现象可以通过裂纹闭合效应解释：裂纹扩展过程的本质影响参数是有效应力强度因子幅度△keff，从式（23）看出载荷由高到低时其数值会先减小，但裂纹扩展门槛值△kth也会减小，短裂纹阶段有如下关系

可知有效应力强度因子幅度又会增大。因此，裂纹扩展速率先减小后增大，反之亦然。从图5中可见，裂纹萌生阶段降序变幅加载时裂纹扩展阶段的裂纹闭合效应影响最小，其次是升序变幅加载，最后是等幅加载。从图4、5中均可见，相同扩展载荷F2max时，随着裂纹长度的增加，各自的扩展速率逐渐接近，当试样断裂时接近相等。这是由于随裂纹扩展的进行，裂纹闭合效应逐渐减弱、最后消失而造成的。

以上现象也可以从损伤角度进行解释。如前文所述，试验中裂纹萌生尺寸都接近0.2 mm，但在不同受力情况下该处的裂纹扩展速率并不相同。由于裂纹扩展速率变化趋势与损伤变量变化率相同，显然裂纹萌生寿命越短，裂纹扩展速率就越大，反之亦然。因此，当用式（23）描述裂纹扩展时，公式右边的a值在变幅情况下小于等幅情况的数值。故当同样用式（23）表示时，u值会增大。由此可以得到相同裂纹扩展载荷加载时，u值与裂纹萌生寿命的变化趋势相反。式（23）中的t值则与裂纹萌生时的应力幅值的变化趋势相同。以上规律不但与如图4、5中所示t、u的变化趋势完全相同而且与裂纹闭合效应描述得相一致。

结合图4、5和表3中的数据，可知裂纹萌生阶段的变幅载荷对裂纹萌生寿命和裂纹扩展寿命影响一致。在最大载荷相同时，等幅加载下的疲劳寿命最短；其次为降序变幅加载；最后为升序变幅加载。

4　结论

（1）结合试验结果，可以通过少量试验数据结合低周疲劳损伤累积模型利用数值方法确定模型中损伤参数的具体数值，进而实现对不同受力情况下裂纹萌生寿命的预估，从而降低试验成本。

（2）结合低周疲劳损伤累积模型对变幅载荷下CT试样的裂纹萌生寿命进行了预测，预测结果与试验数据十分吻合。

（3）结合Paris公式对试验数据进行了拟合，分别从裂纹闭合效应和损伤原理2个角度分析了变幅载荷对裂纹扩展阶段的影响。从试验结果可见，裂纹萌生阶段的变幅载荷对其裂纹萌生寿命和裂纹扩展寿命的影响一致：等幅加载时的疲劳寿命小于变幅加载的疲劳寿命；且升序变幅加载时的疲劳寿命大于降序变幅加载的疲劳寿命。

［1］Kunz L，Lukáš P，Kone ná R.Initiation and propagation of fatigue cracks in cast IN713LC superalloy［J］.Engineering Fracture Mechanics，2010，77（11）：2008-2015.

［2］Andersson H，Persson C，Hansson T.Crack growth in IN718 at high temperature［J］.International Journal of Fatigue，2006，23：817-827.

［3］Burger J L，Biederman R R，Couts W H.The effects of starting condition and the aging response of as-forged alloy 718［C］//Proceedings of the International Symposium on the Metallurgyand and Applications of Superalloy 718，Tms，2004：207-217.

［4］Sundararaman M，Mukhopadhyay P，Banerjee S.Precipitation and room temperature deformation behavior of Inconel 718［C］//Proceedings of the International Symposium on Superalloys 718，625，706 and Various Dervatives S.Tms，1994：419-440.

［5］Manson S S.Behavior of materials under conditions of thermal stress［M］.Washington：NACA，1953：636-370.

［6］Coffin L F Jr.A study of the effect of cyclic thermal stresses on a ductile metal［M］.New York：Knolls Atomic Power Lab，1954，76：931-950.

［7］伍颖.断裂与疲劳［M］.武汉：中国地质大学出版社，2008：93-101. WU Ying.Fracture and fatigue［M］.Wuhan：China University of Geosciences Press，2008：93-101.（in Chinese）

［8］中国航空材料手册编辑委员会.中国航空材料手册［M］.北京：中国标准出版社，2012：323-359. Editorial Board of China Aeronautical Materials Handbook.China aeronautical materials handbook［M］.Beijing：China Standard Press，2012：323-359.（in Chinese）

［9］刘新东，郝际平.连续介质损伤力学［M］.北京：国防工业出版社，2011：180-210. LIU Xindong，HAO Jiping.Continuum damage mechanics［M］.Beijing：National Defense Industry Press，2011：180-210.（in Chinese）

［10］Lemaitre J.Evaluation of dissipation and damage in metals submitted to dynamic loading［J］.Mechanical Behavior of Materials，1972，76（6）：540-549.

［11］Deguang S，Weixing Y.Study on nonlinear continue damage cumulative model for uniaxial fatigue fatigue［J］.Acta Aeronauticaet Astronautica Sinica，1998，19（6）：647-656.

［12］魏大盛，王延荣，王相平，等.基于应力循环特征的裂纹萌生寿命预测方法［J］.航空动力学报，2012，27（10）：2342-2347. WEI Dasheng，WANG Yanrong，WANG Xiangping，et al.Life prediction method based on characteristic of cyclic stress［J］.Journal of Aerospace Power，2012，27（10）：2342-2347.（in Chinese）

［13］Rabotnov Y N.On the equation of state of creep［C］//Proceedings of the Institutionof Mechanical Engineers.Los Angles：SAGE Publications，1963：2117-2122.

［14］Deng G J，Tu S T，Zhang X C，et al.Grain size effect on the small fatigue crack initiation and growth mechanisms of nickel-based superalloy GH4169［J］.Engineering Fracture Mechanics，2015，134：433-450.

［15］Liu N，Gong Z，Tang Y，et al.A study on fatigue damage accumulation based on continuum damage mechanics［C］//Internation Conference on Quality，Reliability，Risk，Maintenance，and Safety Engineering（ICQR2MSE），Chengdu：IEEE，2012：867-870.

（编辑：栗枢）

Effect of Crack Initiation and Propagation Life of High Temperature Alloy under Variable Amplitude

CHU Jin-yang1，SHEN Xiu-li1，2，MAO Jian-xing1，HU Dian-yin1，2，WANG Rong-qiao1，2
（1.School of Energy and Power Engineering，Beihang University，Beijing 100191，China；2.Collaboration Innovation Center of Advanced Aero-engine，Beijing 100191，China；3.AVIC Commercial Aircraft Engine Co.，Ltd.，Shanghai 200241，China）

The low cycle fatigue crack initiation life was regarded as a process of damage accumulation，based on the continuum damage mechanics，a damage accumulation model was established to analyze the influence of variable amplitude at the crack initiation stage of high temperature alloys on the low cycle fatigue crack initiation and propagation life of high temperature materials.With the crack propagation parameters of GQGH4169 alloy at normal temperature，the specific value of damage parameter was determined by finite element and numerical analysis method.Then，crack initiation life predictions were carried out.The results show that the approach can not only predict the crack initiation life of CT specimen accurately，but also reflect a definite influence of crack propagation life under variable amplitude，and the application reduces the cost.

variable amplitude；crack initiation；crack propagation；continuum damage mechanics；high temperature alloy；low-cycle fatigue；aeroengine

V 232.3

A

10.13477/j.cnki.aeroengine.2016.04.014

2015-12-29基金项目：国家自然科学基金（51305012，51375031）资助

初金阳（1990），男，硕士，研究方向为航空发动机结构强度；E-mail：1129388292@qq.com。

引用格式：初金阳，申秀丽，毛建兴，等.变幅载荷对高温合金裂纹萌生及扩展寿命的影响［J］.航空发动机，2016，42（4）：70-75.CHUJinyang，SHENXiuli，MAOJianxing，etal.Effectofcrackinitiationandpropagationlifeofhightemperaturealloyundervariableamplitude［J］.Aeroengine，2016，42（4）：70-75.