机载相控阵PD雷达的MPRF设计与选择
2016-10-24连晓锋汤子跃朱振波汪先超席秋实乔宁
连晓锋, 汤子跃, 朱振波,汪先超, 席秋实, 乔宁
(1.空军预警学院 三系,湖北 武汉 430019; 2.中国人民解放军95028部队,湖北 武汉 430079)
机载相控阵PD雷达的MPRF设计与选择
连晓锋1, 汤子跃1, 朱振波1,汪先超1, 席秋实2, 乔宁1
(1.空军预警学院 三系,湖北 武汉430019; 2.中国人民解放军95028部队,湖北 武汉430079)
针对机载相控阵PD雷达波束宽度随扫描角变化的特点,详细阐述了中脉冲重复频率(MPRF)设计与选择的具体方法步骤。从M/N准则选择、重频范围2方面确定深入研究了MPRF设计问题;从优化模型、约束条件、优化算法3方面深入探讨了MPRF选择问题,提出利用可调参数少、收敛速度快、全局寻优能力强的粒子群算法选择最优MPRF。最后通过具体实例说明了机载相控阵PD雷达MPRF设计与选择方法的有效性。
机载预警雷达;相控阵;脉冲多普勒;MPRF设计;MPRF选择;粒子群优化算法
0 引言
机载相控阵脉冲多普勒(pulse-Doppler,PD)雷达多采用中脉冲重复频率(medium pulse repetition frequency,MPRF)模式。机载相控阵PD雷达在原理上与机扫体制的机载PD雷达相同,但相扫体制的机载PD雷达不同扫描角分配的时间是不一样的,而机扫体制的机载PD雷达所有方位分配的时间是均匀的,这就导致相扫体制与机扫体制的机载PD雷达的MPRF设计和选择是不同的。目前国内外很多学者对机载PD雷达的MPRF设计与选择进行了相关研究,大多针对机扫体制的机载PD雷达提出了很多PRF选择方法。文献[1]通过典型约束全面搜索最优的MPRF组合,复杂、费时;文献[2]提出了噪声环境下的自适应PRF优化选择算法。文献[3-5]运用遗传算法对机载PD雷达的MPRF进行优化选择。文献[6]提出运用模拟退火算法选择最优MPRF。但对采用相扫体制的机载PD雷达的MPRF设计和选择的研究甚少,目前仅有文献[7]对相控阵机载PD雷达PRF设计与选择进行了相关研究,但该文献中脉冲补偿和重频间隔的计算存在偏差,与实际情况不符,需要纠正。
针对机载相控阵PD雷达波束宽度随扫描角变化的特点,本文详细阐述了MPRF设计与选择的具体方法步骤。从M/N准则选择、重频(脉冲重复频率)范围确定深入研究了MPRF设计问题;从优化模型、约束条件、优化算法3方面深入探讨了MPRF选择问题,同时提出利用可调参数少、收敛速度快、全局寻优能力强的粒子群算法选择最优MPRF。
1 机载相控阵PD雷达的MPRF设计
1.1时间资源分配
对于机载相控阵PD雷达,波束宽度随天线扫描角的增大而展宽,导致天线性能下降。为获得全方位比较一致的探测性能,需要增加驻留时间来补偿。工程上通常将相扫的-60°~60°区域分为7个扇区,同一扇区内各波位的扫描间隔相同,波位驻留时间相同。考虑到不同波长在不同扫描角时波瓣展宽程度不同,所以采用的频段不同,分区应有所不同[8]。对于频率在3 GHz以下的机载 相控阵PD雷达,分区1为-60°~-45°,-45°~-30°,-30°~-15°,-15°~15°,15°~30°,30°~45°和45°~60°,对于频率在3 GHz以上的机载相控阵PD雷达,分区2为-60°~-55°,-55°~-45°,-45°~-30°,-30°~30°,30°~45°,45°~55°和55°~60°。
扫描区域内某一个波位上的驻留时间称为景时间,每个波位上的景时间包括各个PRF对应的回波脉冲持续时间(称为帧时间)[9],波位内各个重频分配的时间是相等的。每个PRF的帧时间包含积累时间和填充时间,积累时间内的相干脉冲是用来进行目标检测的。填充时间用以建立稳定的AGC控制,会带来一定的检测损失,对于一般的相控阵雷达而言,各个波位上的填充时间一般是固定的,等于2倍的最大距离除以光速。填充时间内的填充脉冲主要是避免重频切换时前一重频的远距离回波信号混入后一重频的接收信号之中形成干扰,最远处的回波返回之前的脉冲是不能拿来做处理的。
为了方便阐述MPRF设计的过程,这里对机载相控阵PD雷达的相关参数作一个假设。假设某机载相控阵PD雷达采用“平衡木”天线外形,正侧视放置,天线由长方阵组成,负责120°扫描空间,天线阵列为64×16,阵元间距半波长,波长0.15 m,载机速度>120 m/s,正常扫描模式下ts=3.333 3 s,最大作用距离400 km。根据相应的雷达参数,建立分区1后总时间分配为
Ntprf(pac1+pac2+…+pacK)+Ntfill,
(1)
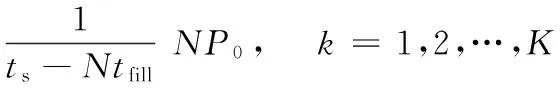
(2)
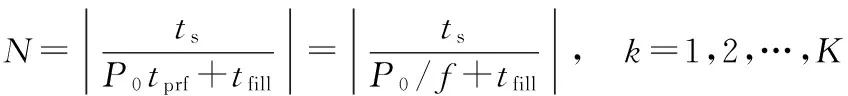
(3)
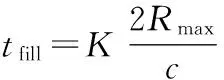
从式(2),(3)可以看出,重频f和重频数N的确定即MPRF组的确定与机载预警雷达的时间资源的分配密切相关,这就决定了重频f和重频数N之间相互制约、相互影响。
另外,根据相控阵雷达波束宽度计算公式可以确定各扇区扫描步长,进而确定各扇区的波位数,同时提出了脉冲补偿因子的概念用以分析相干脉冲。
(1) 波位数
各扇区内的波位数是根据扫描间隔确定的,可以利用相控阵雷达波束控制灵活的特点,根据需要控制扫描间隔,在大扫描角上适当地增大扫描间隔。相控阵方位半功率点波束宽度计算公式为[10]
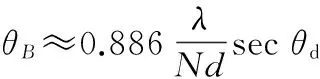
(4)
式中:θd为波束扫描角;d为阵元间距。
相扫的-60°~60°区域内方位向半功率点波束宽度的范围在1.586 5°~3.172 8°之间,平均为2.00 7°,则平均波位数
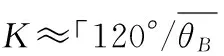
(5)
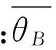
(2) 脉冲补偿
相控阵雷达需要增加积累时间来补偿因波束展宽引起的信噪比损失。各个方位的发射天线增益相比法线方向降低多少,则积累时间补偿多少,其根据是发射天线增益和积累时间在雷达方程中对作用距离的影响是等效的[9]。增加积累时间通过增加相干脉冲数的方法(即脉冲补偿)实现的,各扇区波位内脉冲补偿程度如何确定,本文定义了脉冲补偿因子。脉冲补偿因子:对某一重频,扇区内扫描步长与0°对应扇区内扫描步长的比值。根据计算得出的各扇区内扫描间隔与0°对应扇区内扫描间隔的比值,确定各扇区对应的脉冲数补偿因子分别为2.0,1.4,1.2,1,1.2,1.4,2.0。则脉冲补偿因子和某一重频总的相干脉冲数P0之间关系为
P0=α·p⎣K/2」,
(6)
式中:α为补偿因子的组合;p⎣K/2」为0°扫描角时的相干脉冲数,⎣·」表示向下取整,故
P0=α·p⎣K/2」=(19+1.2×9×2+1.4×7×2+2×5×2)p⎣K/2」=80.2p⎣K/2」.
1.2M/N准则的确立
准则的选择是重频选择算法的前提,M/N准则的确定涉及2方面:一是N的选择,即总的重频个数的确定,这主要从相控阵雷达时间分配角度考虑,确保满足指标要求;二是M的选择,即检测所需重频个数,主要从虚警概率问题考虑。
(1)N的确定
由式(2),(3)可知,重频f和N的确定与天线扫描周期、波位数、各个波位的相干脉冲数和填充时间均有关,天线扫描周期已经给出,波位数、填充时间均可计算,则相干脉冲是N确定的关键因素。由分析可知,0°扫描角对应波位分配的时间最少,只要0°扫描角分配的驻留时间能够满足要求则其他扫描角均可以满足,因各波位的填充时间相同且可计算,所以下面只考察0°扫描角的积累时间。
B⎣K/2」=p⎣K/2」tprf.
(7)
主杂波宽度与相控阵列的波束宽度密切相关,但实际过程中决定主杂波谱宽还有一个重要参数:相干脉冲数。图1给出了相干脉冲与多普勒谱宽的曲线。
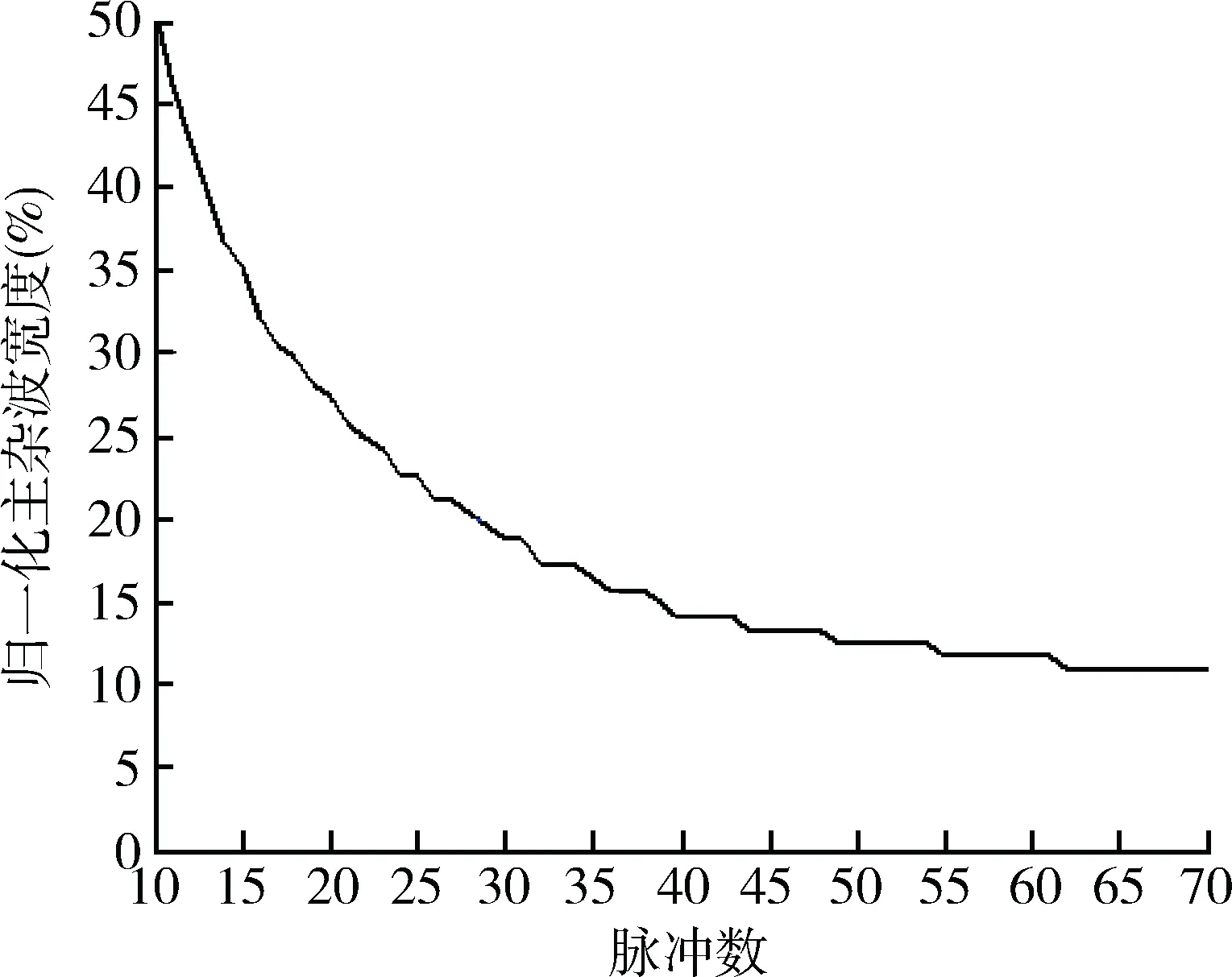
图1 脉冲数与归一化谱宽的关系Fig.1 Relationship between pulse number and normalized spectrum width
从图1中可以看出,若要求主杂波谱宽小于20%,则所需相干脉冲数最少为28左右,所以p⎣K/2」≥cL=28,其中cL为0°扫描角所需的最小脉冲数。主杂波谱宽的确定就对最小脉冲数设置了一个下限,进而对总的重频数设置了一个下限。M/N准则中的N的选择应该满足
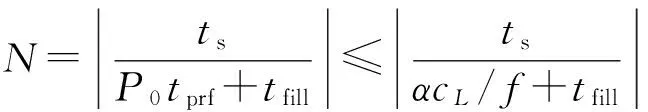
(8)
当重频范围确定时就可以确定重频数的范围,具体重频数的确定提供依据。另外,由于时间的限制,0°扫描角的脉冲数是有上限的,如果脉冲数取的太大会严重影响数据率,所以某一重频0°扫描角的相干脉冲数应该满足
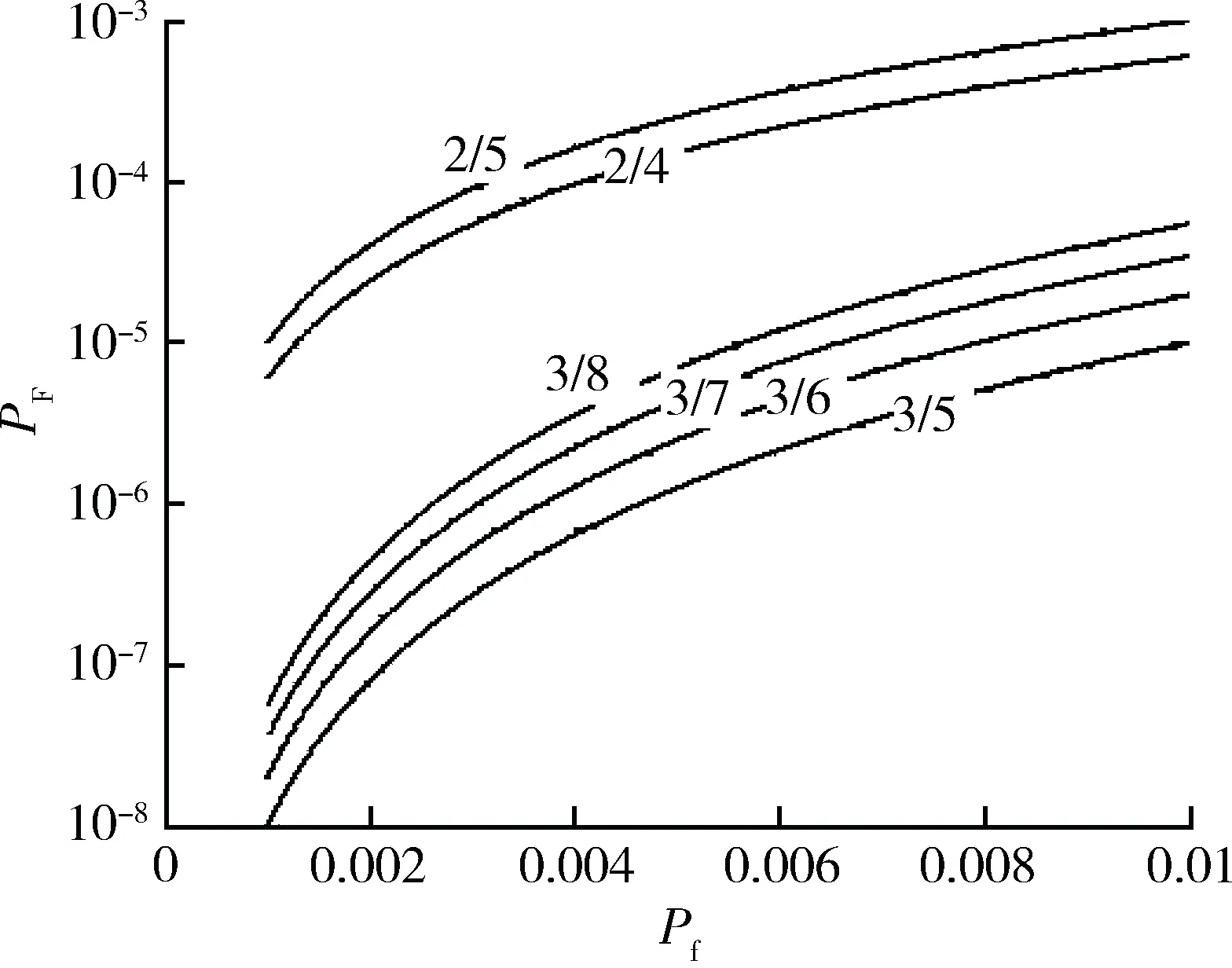
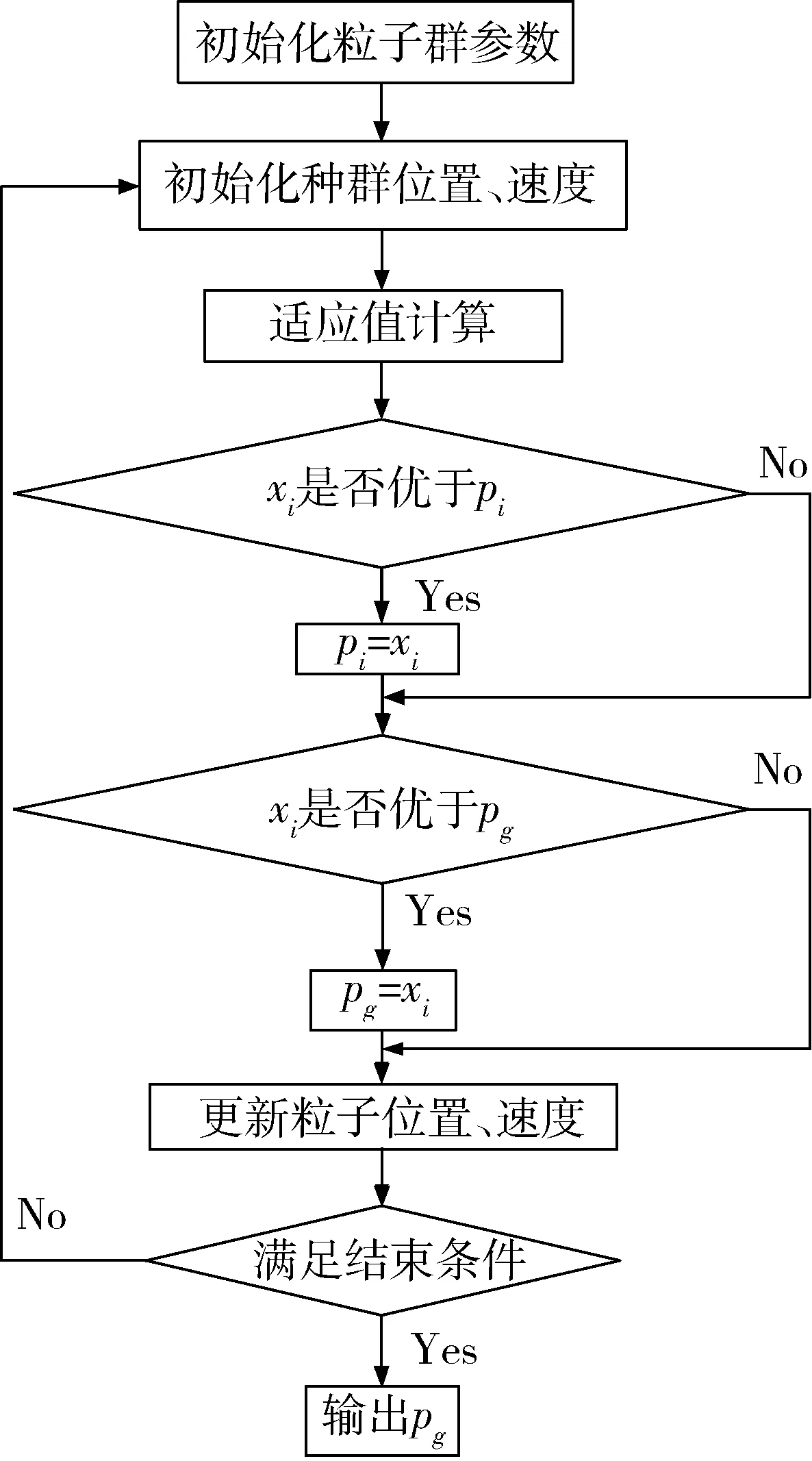
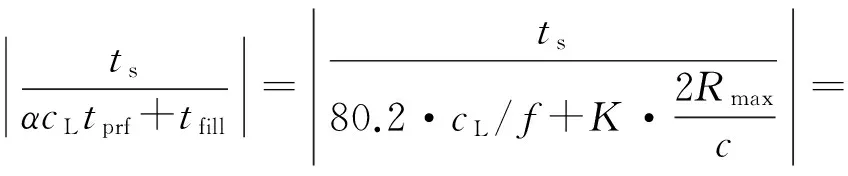
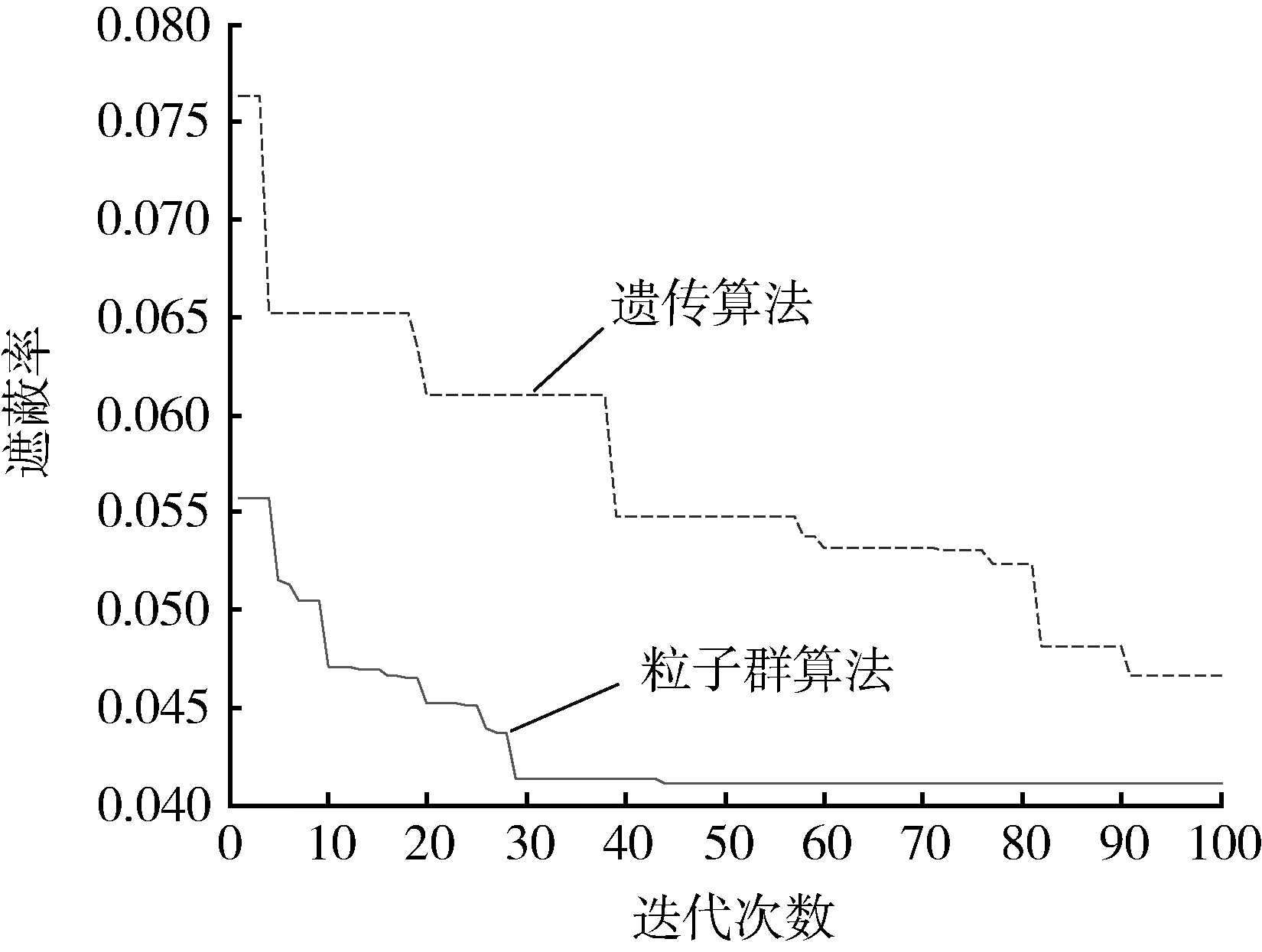
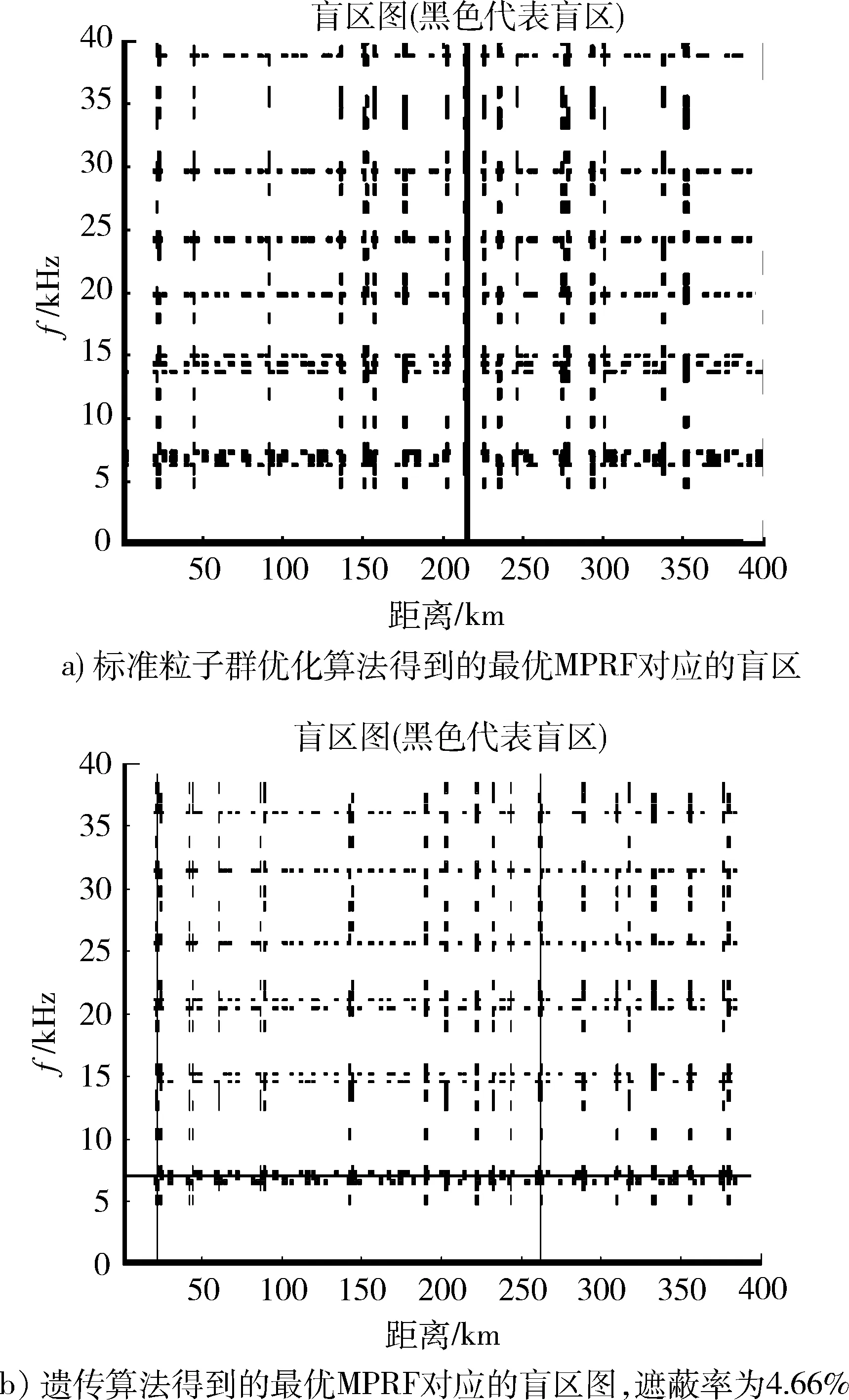
cL≤p⎣K/2」≤cH,cL (9) 式中:cL为下限;cH为上限,一般考虑上限为平均脉冲数 (10) 正因为重频f、重频数N和相干脉冲数是相互制约、相互影响,由式(1)可确定另一相干脉冲数上限 (11) (2)M的确定 对MPRF而言,机载预警雷达一般采用二维CFAR进行恒虚警处理,可以提高目标的信干比,有利于目标检测。这里对于M的选择,只考虑一下M/N准则对虚警概率的影响。最终的虚警概率的计算公式如下: (12) 式中:PF为最终的虚警概率;Pf是恒虚警处理一级所要求的虚警概率。图2中为一些常用的M/N检测准则与虚警率的关系。 图2 Pf与PF虚警率间的关系Fig.2 Relationship between Pf and PF 从图2中可以看出,在Pf一定的情况下,M相同,N减少会降低虚警率;N相同,M增大也会降低虚警率。还需要注意的是M的选择一般在N/2左右的正整数,如典型的3/8准则、3/5准则等。理论上利用两重PRF就能对单个目标距离和多普勒频率进行解模糊。但是,为了降低由于存在多目标所引起的虚警概率,至少需要用三重PRF进行检测。 1.3重频范围的选择 (1) 最小重频的选择 最小重频的选择应从以下几个方面入手: 1) 机载PD雷达中使用MPRF的目的就是为了保证在副瓣杂波中具有良好的检测性能,所以,选择MPRF组时应尽量减小检测单元内副瓣杂波的强度[11]。 (13) 式中:fmc为主瓣杂波抑制宽度(遮挡区);τ为发射脉冲的宽度。 2) 事实上,式(13)给出的是理想的最小重频,但实际上,当M/N准则确定之后从式(2)也可以得出一个最小重频 (14) 3) 另外,对中重频而言,雷达参数确定之后一般要保证载机运动的多普勒频率与重复频率之间满足[7] (15) 式中:γ为正侧面阵时空时二维杂波分布斜率;fd为载机巡航速度时的多普勒频率,γ≥0.9。由式(15)可得 fmin3≥2fdγ. (16) 所以这里选取的最小重频是 (17) (2) 最大重频的选择 最大重频是重频范围的上限,一般考虑占空比的限制,两者关系如下: (18) 式中:du为占空比;τ为发射脉冲的宽度。 事实上式(2)还给出了f1的一个限制,即一般情况下由于时间有限,式中脉冲数是有上限的,即由式(10)和(11)共同确定的脉冲数的上限。这样,搜索重频范围中的最大值应为式(18),而f1重频的范围应该满足 (19) 而第N个重频则应该满足 (20) 在机载预警雷达MPRF设计的基础上,运用粒子群优化算法选择最优MPRF组以满足工程需要。重频组选择的目的旨在解距离模糊和速度模糊的同时,使得距离-速度二维盲区最小,即在M/N准则前提下在最小、最大重频范围内选择最优MPRF组使检测的盲区覆盖率最小。重频组的选择会受到雷达工作性能对其施加的诸多限制和约束,这实际上是一种解大规模组合优化问题[12]。 2.1优化模型 2.2约束条件 机载预警雷达中MPRF的选择还需定义约束条件,改变其中任意一个约束条件都会导致重频选择过程重新进行。本文从强制性约束和选择性约束分别进行了讨论。 (1) 强制性约束 1) 盲区约束 a) 距离除不模糊的低速区外不存在盲区。 b) 速度除不模糊的低速区外不存在盲区。 实际上在距离-速度二维盲区最小的情况下,并不能保证距离除不模糊的低速区外、速度除不模糊的低速区外不存在盲区,不可避免会出现一些盲区[12]。 2) 重频选择范围 根据式(19),(20)可以确定最小频率和最大频率的范围。 3) 解模糊 (21) (22) 式中: Rmax最大作用距离;Dmax为最大多普勒频率。式(21)和(22)保证解模糊的正确性。 (2) 选择性约束 1) 重频间隔 重频的间隔是为了保证在M/N准则下所有距离的特定速度上的盲区不存在。重频间隔应满足: (23) 2) 数值约束 数值约束是指对重复频率值的约束,本文要求重复频率值互为素数。 2.3粒子群算法 粒子群优化(partical swarm optimization,PSO)算法是近年来发展起来的一种新的基于叠代的进化算法[14],种群中每个成员叫做粒子,代表着一个潜在的可行解[15],而食物的位置代表全局最优解。每个粒子都有自己的位置和速度(决定飞行的方向和距离),以及一个由被优化函数决定的适应度值。每次迭代中,粒子通过跟踪2个最优解动态调整自己的速度和位置,最终接近食物的位置,达到从全空间搜索最优解的目的:一个是粒子自身找到的最优解,叫做个体最优解;另一个是种群找到的最优解,叫做全局最优解。粒子可以看作是D维空间中的一点,把第i个粒子的位置表示为xi(t)=(xi1,xi2,…,xiD),而把速度表示为vi(t)=(vi1,vi2,…,viD),个体最优解表示为pi(t)=(pi1,pi2,…,piD),所有粒子中全局最优解的下标用g表示。粒子速度和位置的更新方程如下[13] vid(t+1)=vid(t)+c1r1(pid(t)-xid(t))+ c2r2(pgd(t)-xid(t)), (24) (25) xid(t+1)=xid(t)+vid(t+1), (26) 图3 PSO流程图Fig.3 Flow chart of PSO 本文运用Matlab编程工具,对基于标准粒子群优化算法的最优PRF组的选择方法进行仿真实验,并与遗传算法的求解结果进行对比。 粒子群算法参数:迭代次数M=200,种群规模N=30,Vmax=fmax-fmin,Vmin=fmin-fmax,c1=c2=1.494 45,以二维盲区遮蔽率作为个体适应值。 则各种约束值为 则 N最大值范围3~8之间,从时间资源分配角度考虑N取5比较合适。选取3/5准则,不仅能满足解模糊的需要,还能很好减小“重影”影响,则 4 455.6 Hz, 所以cH的范围在36~48之间,这里选42(1/2频率间隔)。即各重频的范围 6 683.3 Hz≤f5≤fmax=7 700 Hz, fi-1≤fi≤fi+1,i=2,3,4, 则149≤tprf1≤224,130≤tprf5≤150。 运用标准粒子群优化算法搜索得到的脉冲重复频率为prf=[5 957,6 298,6 646,6 982,7 692] (Hz)。0°扫描角的相干脉冲数是38,40,42,44,48。运用遗传算法搜索得到的脉冲重复频率为prf=[5 210,6 329,6 771,7 127,7 439]。图4给出了2种算法的最优MPRF的迭代过程,图5给出了2种算法的最优MPRF对应的盲区图。 图4 选择最优MPRF的迭代过程Fig.4 Iterative process of selecting the optimal MPRF 图5 最优MPRF对应的盲区图Fig.5 Blind spot corresponding to the optimal MPRF 从图4中可以看出,标准粒子群优化算法相比遗传算法收敛要快。从图5中可以看出,标准粒子群优化算法所得到的遮蔽率优于基于遗传算法得到的遮蔽率,所提算法能取得较好的效果。 针对机载相控阵PD雷达波束宽度随扫描角变化的特点,本文详细阐述了MPRF设计与选择的具体方法步骤。实验表明,本文所提方法能得到所需MPRF组,满足机载相控阵PD雷达的工作需要,为机载相控阵PD雷达的MPRF波形设计提供了依据。 [1]SIMPSON J. PRF Set Selection for Pulse Doppler Radars [C]∥The IEEE Region 5 Conference, 1988: 38-44. [2]MOORMAN R A, WESTERKAMP J J. Maximizing Noise-Limited Detection Performance in Medium PRF Radars by Optimizing PRF Visivility[C]∥Proc. IEEE National Aerospace and Electronics Conference, July 1993,Vol. l:288-293. [3]DAVIES P G, HUGHES E J. Medium PRF Set Selection Using Evolutionary Algorithms[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(3): 933-939. [4]ALABASTER C M, HUGHES E J, MATTHEW J H.Medium PRF Radar PRF Selection Using Evolutionary Algorithms[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003,39(3): 990-1001. [5]ALABASTER C M, HUGHES E S. The Design of Medium PRF Radar Schedules for Optimum Delectability in Diverse Clutter Scenes[C]∥ Proc. IEEE Waveform Diversity and Design, 2006. [6]Soyeon Ahn, Heedeok Lee, Byungwook Jung. Medium PRF Set Selection for Pulsed Doppler Radars Using Simulated Annealing[C]∥IEEE National Radar Conference-Proceedings,2011,10(1):91-94. [7]侯耀清,陈辉,母其勇.相控阵机载PD雷达的波形设计问题[J]. 雷达科学与技术, 2007,5(1): 22-28. HOU Yao-qing, CHEN Hui, MU Qi-yong. Waveform Design for Phased-Array PD Radar[J]. Radar Science and Technology, 2007,5(1):22-28. [8]张晓波, 曹晨. 机载预警雷达最优探测波长研究[J]. 中国电子科学研究院学报, 2011,6(3): 263-266. ZHANG Xiao-bo, CAO Chen. A Study on Airborne Early Warning Radar Optimal Detection Wavelength[J]. Journal of CAEIT, 2011, 6(3): 263-266. [9]曹晨. 机载相控阵PD雷达性能分析中的重要问题[J]. 现代雷达, 2008, 30(6):14-16. CAO Chen. Problems in Airborne Phased-Array PD Radar Performance Analysis[J]. Modern Radar, 2008, 30(6): 14-16. [10]张光义. 相控阵雷达原理[M].北京:国防工业出版社,2009:29-30. ZHANG Guang-yi.The Theory of Phase Array Radar[M].Beijing:National Defence Industry Press,2009:29-30. [11]陈国海. 机载脉冲多普勒雷达的中脉冲重复频率的波形设计[J]. 现代雷达, 1999,21(1):14-18. CHEN Guo-hai. MPRF Wave-Form Design for Airborne PD Radar[J]. Modern Radar,1999,21(1):14-18. [12]韩伟. 机载预警雷达航迹综合优化技术研究[D]. 武汉: 空军预警学院, 2009. HAN Wei. Study on the Synthesis Optimization of Airborne Early Warning Radar Track[D]. Wuhan: Airforce Early Warning Academy, 2009. [13]王鹏, 谭贤四, 王红, 等. 基于遗传算法的地面中重频PD雷达PRF组选择[J]. 现代雷达, 2008, 30(9):33-35. WANG Peng, TAN Xian-si, WANG Hong, et al. PRF Set Selection for Ground-Based MPRF PD Radars Based on Genetic Algorithm[J]. Modern Radar, 2008, 30(9): 33-35. [14]沈伋, 韩丽川, 沈益斌. 基于粒子群算法的飞机总体参数优化[J]. 航空学报, 2008, 29(6):1538-1541. SHEN Ji, HAN Li-chuan, SHEN Yi-bin. Optimization of Airplane Primary Parameters Based on Particle Swarm Algorithm[J]. Acta Aeronautica et Astronautica Sinca, 2008, 29(6):1538-1541. [15]KENNEDY J, EBERHART R C. Particle Swarm Opti mization[C]∥Proc. IEEE International Conference on Neural Networks, 1995:1942-1948. MPRF Design and Selection of Airborne PD Radar LIAN Xiao-feng1, TANG Zi-yue1, ZHU Zhen-bo1, WANG Xian-chao1,XI Qiu-shi2, QIAO Ning1 (1. Air Force Early Warning Academy,Department 3,Hubei Wuhan 430019, China;2. PLA,No.95028 Troop,Hubei Wuhan 430079, China) The detailed methods and steps of medium pulse repetition frequency(MPRF) design and selection are described based on the characteristics of phase array radar. The MPRF design problem is analyzed fromM/Nscheme selection and the pulse recurrence frequency(PRF) range, and The MPRF selection problem is discussed from three aspects of optimization model, constraints and optimization algorithm. Swarm optimization algorithm is developed to select optimum MPRF, for the algorithm has simple realization process, less adjustable parameters, higher convergence speed and stronger global optimization. Finally, an example is given to demonstrate the effectiveness of the proposed MPRF design and selection method. airborne early warning radar; phase array; pulse-Doppler(PD); medium pulse repetition frequency(MPRF) design; MPRF selection; particle swarm optimization 2015-05-18; 2015-10-15 青年创新基金(2013QNCX0101);中国博士后科学基金(2015M572779) 连晓锋(1990-),男,河北石家庄人。硕士生,主要研究方向为目标检测与识别。 通信地址:430019武汉市江岸区黄浦大街288号空军预警学院3系E-mail:1248656228@qq.com 10.3969/j.issn.1009-086x.2016.04.021 TN959.73;TN958.92 A 1009-086X(2016)-04-0129-07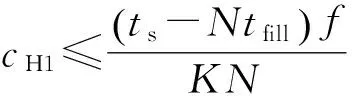
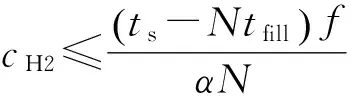
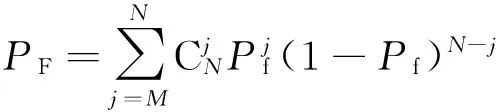
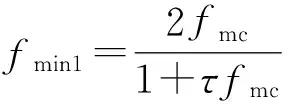
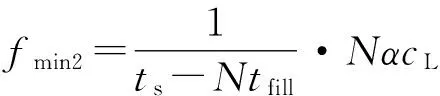
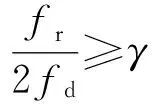
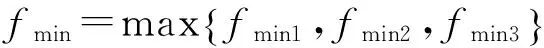
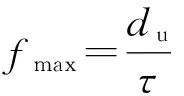
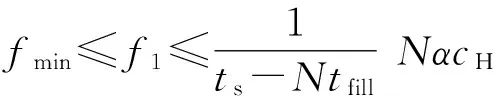
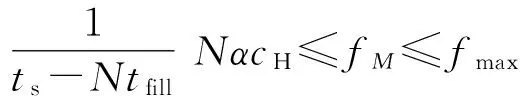
2 机载预警雷达MPRF选择

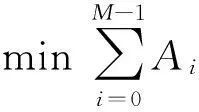
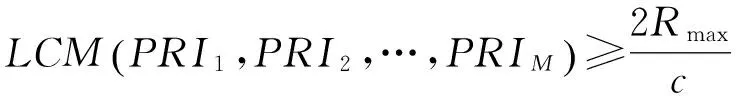
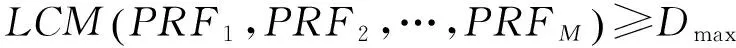
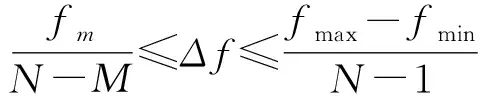
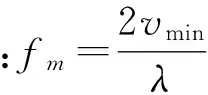
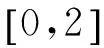

3 仿真分析
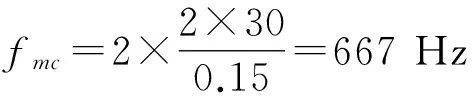
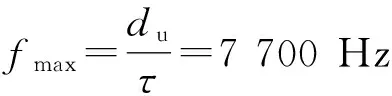
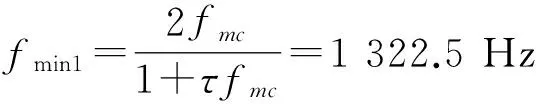
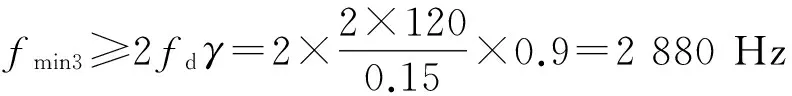
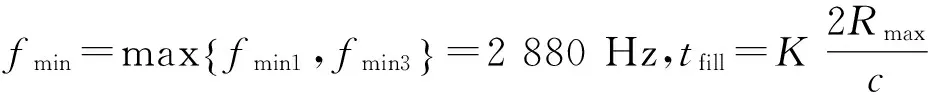
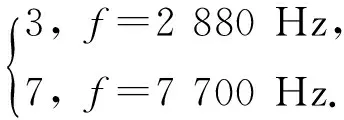
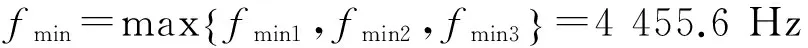
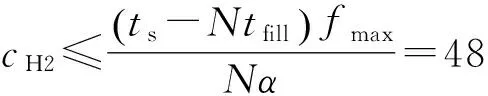
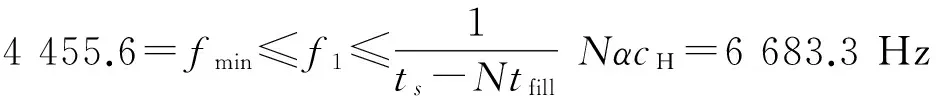
4 结束语
