含特征点飞行器位置参数的样条微分平滑方法
2016-10-24陈晶李国友黄维张新兰
陈晶,李国友,黄维,张新兰
(中国人民解放军95948部队,甘肃 兰州 732750)
含特征点飞行器位置参数的样条微分平滑方法
陈晶,李国友,黄维,张新兰
(中国人民解放军95948部队,甘肃 兰州732750)
为了获取准确的飞行器速度参数,根据含特征点的飞行器轨道特点,提出了一种基于最优节点样条逼近的微分平滑算法。首先给出了含特征点轨道位置参数样条微分平滑问题的数学模型;其次介绍了特征点的识别方法;然后建立了基于混沌粒子群算法的样条微分平滑算法;最后给出了典型情况下的仿真结果。仿真结果表明:该方法可以有效减小随机误差和截断误差的影响,提高含特征点飞行器轨道速度参数计算精度。
飞行器;位置参数;微分平滑;特征点;样条节点;粒子群优化
0 引言
在光测数据事后处理中,通常采用多台光学经纬仪进行空间交会获取飞行器位置参数,再进行正交多项式中心微分平滑,获取飞行器速度参数。选择多项式阶数和平滑区间长度需要综合考虑随机误差和截断误差影响,在运动变化较大时,特别是在含有特征点(如主动段关机点、级间分离点)的段落,采用多项式微分平滑存在较大的截断误差,影响速度参数的准确性[1]。
文献[2-7]的研究表明,飞行器的轨道位置参数可用3次B样条函数高精度逼近。利用样条函数的可微性可以获取飞行器速度参数。文献[8-10]通过优化样条节点分布适应目标运动规律,在运动变化较大段落节点分布较密,减小了截断误差;在运动变化缓慢段落节点分布稀疏,减小了随机误差。但在样条节点优化过程中,需要利用对数变换将有约束问题转化为无约束问题,并需要计算待优化函数的雅克比矩阵,算法复杂,并且没有考虑飞行器轨道特征点识别。
本文针对含有特征点的飞行器轨道位置参数的样条微分平滑问题,采用遥测数据或光测图像确定飞行器轨道特征点时刻,将特征点作为固定样条节点,采用混沌粒子群算法对其余节点进行优化分布,实现了对含特征点飞行器轨道位置参数的高精度样条逼近,减小了截断误差和随机误差影响,并且不需要计算优化函数的雅克比矩阵,降低了算法复杂程度。
1 问题的数学描述
飞行器轨道受力变化导致加速度突变的点被称为轨道特征点,如主动段关机点、级间分离点等,当特征点被确定为样条节点时,飞行器轨道空间位置参数可以用3次B样条函数进行高精度表示[11]。
假设多台光电经纬仪在t1~tm时间段内对飞行器进行跟踪测量,进行外测数据事后处理通过空间交会得到轨道位置参数(x(ti),y(ti),z(ti))T,ti∈[t1,tm]。
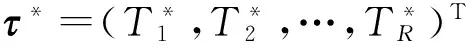
下面以y方向位置参数的样条微分平滑为例进行说明。飞行器ti时刻y方向位置参数y(ti)可以表示为
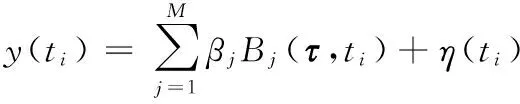
(1)
式中:Bj(τ,ti)为以τ为样条内节点的3次规范B样条基函数
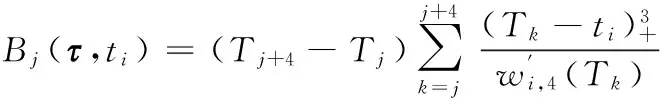
(2)
βj为轨道参数y方向的样条系数;η(ti)为飞行器轨道y方向位置参数的测量误差。
定义A(τ)为以τ为样条内节点的样条基矩阵
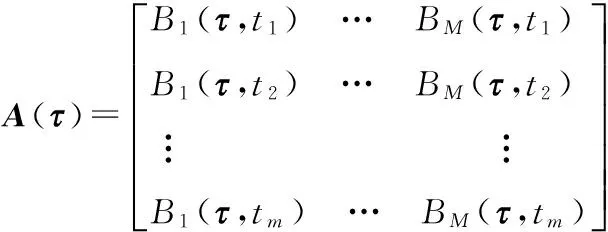
(3)
则轨道y方向位置参数向量可以表示为
Y=A(τ)β+η,
(4)
式中:Y=(Y(t1),…,Y(tm))T为外测数据事后处理得到的飞行器y方向位置参数向量;β=(β1,…,β3M)T轨道y方向位置参数样条系数向量;η=(η(t1),…,η(tm))T为y方向位置参数的误差向量。
通过交会计算得到的飞行器位置参数的误差并不是等方差的,定义
E(ηηT)=P,P=diag(σ2(t1),…,σ2(tm)),
式中:σ2(ti)为ti时刻飞行器y方向位置参数随机误差方差。
定义待优化目标函数为残差平方和
Q(τ,β)=‖P-1/2Y-P-1/2A(τ)β‖2,
(5)
位置参数的样条微分平滑问题就是对τ,β进行估计,使得
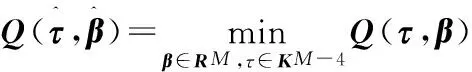
(6)


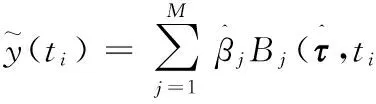
(7)
利用样条函数的可微性可以对轨道位置参数进行微分计算得到速度参数
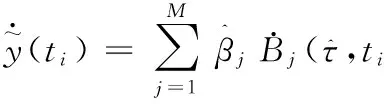
(8)
含特征点飞行器位置参数的样条微分平滑问题等价于先对样条内节点序列τ进行优化,然后对轨道参数的样条系数向量β进行估计的优化问题。在优化过程中,不仅需要考虑样条内节点序列τ自身的时间先后顺序约束条件,即t1 实际飞行器外测数据事后处理过程中,轨道特征点序列τ*并非已知量,准确定位飞行器轨道特征点成为轨道位置参数样条微分平滑的前提。 飞行器的主动段关机、级间分离、二级点火等特征时刻,飞行器光测图像会有明显变化,可以直接通过光测图像进行特征点确定。当飞行器具有遥测数据时,可以直接利用遥测的视加速度数据确定轨道特征点[12]。通过飞行器平台安装的3个加速度表,测量沿惯性坐标系3个方向的视加速度,视加速度发生突变的点就是飞行器轨道的特征点。值得注意的是,由于遥测系统和外测系统在采样频率、时间零点等方面存在差异,需要对遥测数据进行必要的对齐和修正。 特征点序列确定后的位置参数样条微分平滑问题是一个带有复杂约束条件的非线性优化问题,传统的高斯-牛顿法难以完成寻优计算[13]。混沌粒子群算法是一种群体智能优化算法,通过引入混沌思想,既具有粒子群算法简单、易于编程实现的优点,又克服了复杂函数优化的早熟收敛问题,可用于解决特征点序列确定后样条节点优化这类复杂的非线性优化问题[14]。 3.1适应度计算 在粒子群算法中,需要利用适应度值判断粒子的优劣,对于特征点序列确定后的样条微分平滑问题,采用样条逼近残差平方和Q(τ′,β)作为适应度值。 计算粒子Γi的适应度值步骤如下: (1) 将Γi和τ*合并,按从小到大排列得到样条内节点序列为τ=(T5,T6,…,TM)T,进行节点延拓后得到总的节点序列T1 (2) 计算样条基矩阵,根据式(2)计算样条内节点序列τ对应的样条基函数,代入式(3)计算得到样条基矩阵A(τ)。 (3) 将A(τ)代入式(4),进行马尔可夫估计得到样条系数向量的估计值 (9) (10) 3.2粒子位置更新 粒子i根据下面的公式更新位置和速度 (11) (12) 式中:c1和c2为学习因子常数;r1和r2为[0,1]之间的随机数;εd为小于飞行器轨道位置参数时间采样间隔的小量。 3.3全局最优位置的混沌优化 在复杂优化问题中,粒子群算法易产生早熟收敛问题,陷入局部极值点,因此引入混沌粒子群算法克服这一问题。根据全局最优位置采用混沌映射产生混沌序列种群,然后利用混沌序列种群中的最优粒子随机替代当前种群中的某个粒子[15]。 (13) 3.4算法流程 采用混沌粒子群算法进行特征点确定后的样条节点位置优化的流程为 步骤1:初始化粒子群算法基本参数。根据自由样条内节点个数D,计算初始样条节点间隔h=(tm-t1)/D,设置最大粒子速度为,vmax=h设置学习因子c1,c2,设置粒子群种群规模maxS,设置最大进化代数maxE,设置混沌迭代最大次数maxL。 步骤2:初始化种群,随机生成maxS个自由样条内节点粒子 Γi=t1+rand(1,D)·(tm-t1), (14) 式中:rand(1,D)为取值介于[0,1]之间的1×D维随机数向量。 粒子Γi的速度初始化为 Vi=-vmax+rand(1,D)·2vmax. (15) 初始化粒子Γi的最好位置为Pi=Γi,计算每个粒子对应的适应度值Ei,初始化每个粒子的最优适应度值Eibest=Ei,初始化全局最优适应度Ebest为向量(E1best,…,EDbest)T的最小值,对应的粒子存入种群的全局最优位置Pg,进化代数设置为Gn=1。 步骤3:根据式(11),(12)对每个粒子位置和速度进行更新,计算每个粒子的适应度Ei,比较Ei和Eibest,若Ei 步骤4:对全局最优位置Pg进行混沌优化,用混沌种群中的最优粒子随机代替原种群中的某个粒子,进化代数Gn=Gn+1。 步骤5:判断是否达到最大进化代数或全局最优适应度值是否满足精度要求,若没有满足则转入步骤3继续进行迭代,否则转入步骤6。 步骤6:输出全局最优适应度Ebest和全局最优位置Pg。 4.1仿真条件 利用某型飞行器0~60 s的理论轨道数据进行仿真,其中包含两处特征点。根据光电经纬仪站址生成2台光测设备的角度观测数据,添加小于15″的随机误差。根据2台光电经纬仪的仿真角度数据进行空间交会定位,得到飞行器轨道位置参数测量值(输出时间间隔为0.1 s)。 4.2仿真方案 分别采用如下3种方法对y方向位置参数测量值进行微分平滑,得到y方向速度分量vy,与y方向速度分量理论值进行比较。 方案1:采用21点二阶多项式进行多项式中心微分平滑; 方案2:采用文献[2]方法进行样条微分平滑,样条内节点数设置为20个; 方案3:采用本文方法进行样条微分平滑,样条内节点数设置为20个(其中包含2个特征点)。 4.3仿真结果 3种微分平滑方法得到的与理论值之间差别的均方差如表1所示。 表1 vy误差均方差对比 特征点时刻vy与理论值之间差别的绝对值如表2所示。 表2 特征点时刻vy误差绝对值对比 为直观起见,3种方法得到的vy与理论值在特征点1的局部放大效果如图1所示。 图1 不同方法在特征点1的速度分量曲线Fig.1 Velocity curve of characteristic point 1 with different methods 由表1,2和图1仿真结果可知,与另外2种方法相比,采用本文方法对飞行器位置参数进行微分平滑得到的速度分量更接近理论值,特别是在特征点时刻优势更为明显,有效减小了截断误差和随机误差。 本文在含有特征点的飞行器非平稳飞行段落,利用遥测数据或者光测图像预先分析出这些特征点,以特征点为样条内节点,采用粒子群算法对其余样条内节点进行优化分布,可以有效减小轨道位置参数样条微分平滑的随机误差和截断误差,可用于光测数据事后处理的飞行器位置参数微分平滑,提高速度参数的计算精度。 [1]柴敏,胡绍林,郭小红.外测弹道截断误差修正方法[J].导弹与航天运载技术,2006(5):53-57.CHAI Min,HU Shao-lin,GUO Xiao-hong. Research on Algorithm for Truncation Error of Exterior Measured Trajectory[J]. Missile and Space Vehcile,2006(5):53-57. [2]王菖,段晓君,王正明,等.B样条分频理论及在外测数据处理中的应用[J].弹道学报,2010,22(3):99-102. WANG Chang, DUAN Xiao-jun, WANG Zheng-ming, et al. B-Spline Separating Signals Method and Its Application in Measured Data Post-Processing[J]. Jounal of Ballistics, 2010, 22(3):99-102. [3]周海银,李董辉,蒋月评. 基于多源信息融合的飞行器高精度定位方法[J]. 湖南大学学报:自然科学版,2007,34(4):37-40. ZHOU Hai-yin,LI Dong-hui,JIANG Yue-ping. High Precision Method for Determining the Position of Aircraft based on Multi-Sensors Information Fusion[J]. Journal of Hunan University:Natural Sciences ed,2007,34(4):37-40. [4]张艳,石晟玮,郭军海. 基于样条约束的弹道融合抗差估计方法[J]. 弹道学报,2011,23(1):40-44. ZHANG Yan, SHI Sheng-wei, GUO Jun-hai. Robust Estimation for Trajectory Fusion Based on Spline Restraint[J]. Journal of Ballistics,2011,23(1):40-44. [5]贺明科,王正明. 光学接力跟踪的弹道融合[J]. 弹道学报,2002,14(1):1-7. HE Ming-ke,WANG Zheng-ming. Fusion of Trajectory Tracked by Relay Optical Measure System[J]. Journal of Ballistics,2002,14(1):1-7. [6]朱武宣,高耀文. 基于样条约束“EMBET”的再入轨道测量数据融合方法[J]. 飞行器测控学报,2005,24(6):49-53. ZHU Wu-xuan,GAO Yao-wen. A Data Fusion Method for Reentry Ballistic Measurement with Spline Restraint EMBET[J]. Journal of Spacecraft TT&C Technology,2005,24(6):49-53. [7]赵文策,周海银,段晓君,等. 基于测角元和高程信息融合的弹道定位求速[J]. 弹道学报,2004,16(2):27-32. ZHAO Wen-ce,ZHOU Hai-yin,DUAN Xiao-jun,et al. Trajectory Positioning and Velocity Determination Based on Angle Measurement and Height Information Fusion[J]. Journal of Ballistics,2004,16(2):27-32. [8]郭文胜,宫志华,董立涛,等.雷达测距拟合微分求速方法研究[J].现代雷达,2010,32(8):33-37. GUO Wen-sheng, GONG Zhi-hua, DONG Li-tao, et al. A Study on Getting Radar Radial Velocity by Range Fitting and Differential Method[J]. Modern Radar, 2010, 32(8):33-37. [9]易东云,朱炬波,王正明.三频带信号分离的样条函数方法[J].电子学报,1999(1):54-57. YI Dong-yun, ZHU Ju-bo, WANG Zheng-ming. Three Bands Seperating Signal Method with Spline Function[J]. Jounal of Electronics, 1999(1):54-57. [10]郭军海. 基于最优节点样条逼近的观测数据平滑方法[J]. 中国空间科学技术,2000(3):43-48. GUO Jun-hai. A Measurements Smoothing Method Based on Optimal Knots Spline Approximation[J]. Chinese Space Science and Technology, 2000(3):43-48. [11]潘建平,赵文策,甘友谊.基于测量数据误差特性求解轨道参数的方法[J].飞行器测控学报,2009,28(1):52-55. PAN Jian-ping, ZHAO Wen-ce, GAN You-yi. Computation of Trajectory Parameters Based on Error Characteristics of Measurement Data[J]. Journal of Spacecraft TT&C Technology, 2009, 28(1):52-55. [12]赵文策,潘建平,陈伟利.基于弹道动力特性考虑的不完全测量数据处理方法[J].飞行器测控学报,2006,25(6):64-68. ZHAO Wen-ce, PAN Jian-ping, CHEN Wei-li. The Processing Method of Incomplete Instrumentation Data Based on Consideration of Trajectory Dynamic Characteristics[J]. Journal of Spacecraft TT&C Technology, 2006, 25(6):64-68. [13]王召刚,袁林,玄志武.PSO节点寻优的样条逼近微分[J].飞行器测控学报,2012,31(2):45-48. WANG Zhao-gang, YUAN Lin, XUAN Zhi-wu. Spline Approximation Diferential with PSO Knot Placement Majorization[J]. Journal of Spacecraft TT&C Technology, 2012, 31(2):45-48. [14]李邓化,李金鳌,庞美枫,等.基于惯性因子的混沌粒子群优化算法[J].北京信息科技大学学报,2012,27(5):7-10. LI Deng-hua, LI Jin-ao, PANG Mei-feng, et al. Research on Chaos Particle Swarm Optimization Algorithm Based on Inertia Weight[J]. Journal of Beijing Information Science and Technology University, 2012, 27(5):7-10. [15]胥小波,郑康峰,李丹,等.新的混沌粒子群算法[J].通信学报,2012,33(1):24-30. XU Xiao-bo, ZHENG Kang-feng, LI Dan, et al. New Chaos Particle Swarm Optimization Algorithm[J]. Journal on Communications, 2012, 33(1):24-30. Method of Spline Differential Flatness for Position Parameters of Spacecraft with Characteristic Points CHEN Jing,LI Guo-you,HUANG Wei,ZHANG Xin-lan (PLA,No. 95948 Troop, Gansu Lanzhou 732750, China) To obtain the accurate velocity parameters of spacecraft, according to the characteristics of spacecraft orbit with characteristic points, a differential flatness algorithm based on optimal knots spline is proposed. Firstly, the math model of spline differential flatness for position parameters of spacecraft orbit with characteristic points is put forward. Secondly, the recognition method for characteristic points is introduced. Then, the spline differential flatness algorithm based on chaos particle swarm optimization is set up. Finally, the simulation results in typical cases are supplied. The simulation results show that this method can reduce the influence of truncation error and random error, and the accuracy of velocity parameters of spacecraft orbit with characteristic points can be improved. spacecraft; position parameters; differential flatness; characteristic point; spline knots; particle swarm optimization 2015-07-30; 2016-02-30 陈晶(1978-),男,辽宁锦州人。工程师,学士,从事靶场光电测量总体论证研究。 通信地址:732750兰州市27支局16信箱1号E-mail:xdliguoyou@163.com 10.3969/j.issn.1009-086x.2016.04.011 V556.3;TP391.9 A 1009-086X(2016)-04-0061-052 轨道参数特征点的确定方法
3 样条微分平滑的粒子群优化算法

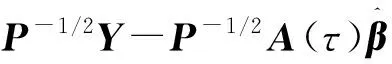
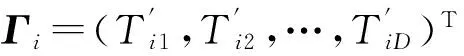

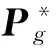
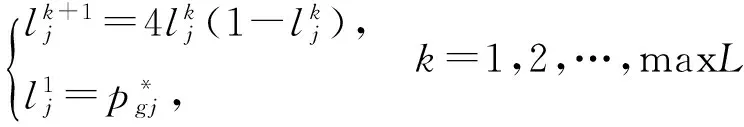
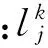
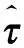
4 仿真验证


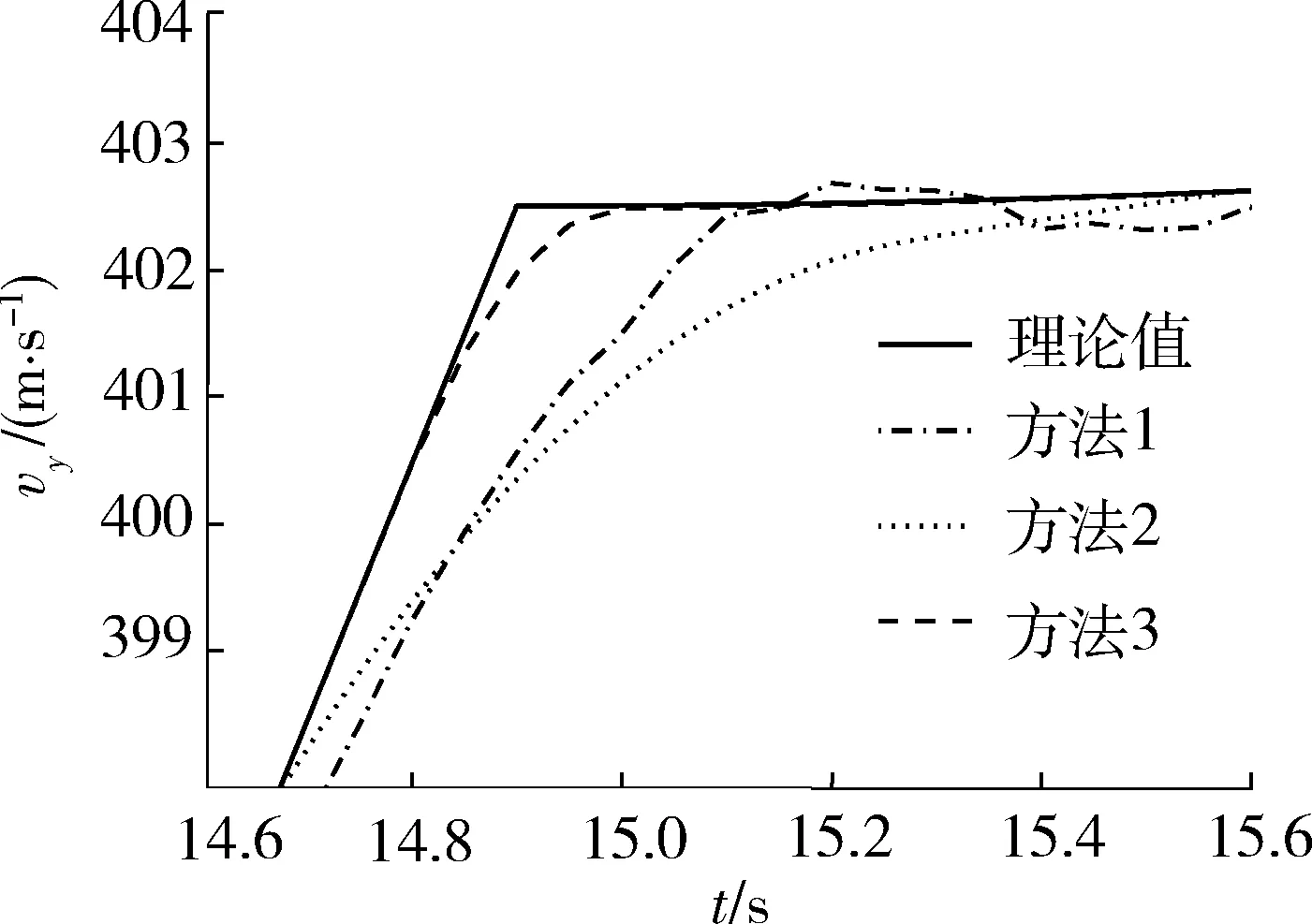
5 结束语
