高阶控制导弹自适应滑模制导律

花文华，孟庆龄，张金鹏,

(1. 中国空空导弹研究院，河南 洛阳　471009； 2. 航空制导武器航空科技重点实验室，河南 洛阳　471009)



高阶控制导弹自适应滑模制导律

花文华1，孟庆龄2，张金鹏1,2

(1. 中国空空导弹研究院，河南 洛阳471009； 2. 航空制导武器航空科技重点实验室，河南 洛阳471009)

为改善制导精度，提高对目标信息滤波器估计误差的鲁棒性，提出了一种滤波器加自适应滑模制导律的设计方法。滤波器提供制导律执行所需的必要信息，如目标加速度等，而自适应滑模制导律进一步增强对信息估计误差的鲁棒性，同时由于采用了自适应设计，避免了对干扰或误差上界保守估计所带来的制导性能损失。滤波器和滑模制导律从一般意义上进行设计，可适用于拦截导弹和目标具有高阶控制动态的情形。基于Monter Carlo法进行了仿真验证，结果表明相比于最优制导律具有较强的鲁棒性和制导性能优势。

制导律；滑模控制；高阶控制；自适应控制；滤波器估计误差；Monter Carlo仿真

0　引言

经典制导律，如比例导引并不要求准确的目标加速度信息，脱靶量可通过相对目标的机动性能优势保证，弹目机动性能比一般大于3。而对于现代制导律，对机动性能的要求下降，但为保证脱靶量，往往就需要目标的相关信息[1-2]，如加速度等，而目标加速度是无法直接量测的，需要基于相关量，如视线角的噪声量测进行观测或重构。因此最终的制导精度受限于滤波器的性能，包括精度、延迟等。为进一步改善制导精度，提高对目标加速度估计误差的鲁棒性，本文提出一种滤波器加滑模制导律的设计方法，滤波器提供制导律执行所需的信息，而通过滑模制导律[3-8]设计增强对滤波器估计误差的鲁棒性，从而改善制导性能。

1　问题描述及建模

制导末端的弹目相对运动关系如图1所示，x轴沿初始视线方向，下标P和E分别表示拦截导弹和目标的相关状态，a，v和γ为相应的加速度、速度和航向角，y表示拦截导弹和目标相对于初始视线方向的位移。基于下述假设进行问题的分析：

(1) 拦截导弹和目标二者可近似为具有线性动态特性的质点，并可沿初始视线方向进行线性化；

(3) 二者控制系统动态满足最小相位特性。

图1　平面相对运动关系Fig.1　Planar engagement geometry

基于图1和假设(1)，拦截导弹和目标相对运动关系可近似表示为

(1)

(2)

假设拦截导弹控制系统阶数为n，则其控制系统可表示为

(3)

参考拦截导弹，具有m阶的目标控制系统可表示为

(4)

式中：d1,d2≥0；uEc为目标控制命令。

定义状态变量x=(y，v，aE，pE，aP，pP)T，则系统状态方程可表示为

(5)

基于假设(1)和假设(2)，拦截导弹飞行时间为

tf≈r0/vc,

(6)

式中:r0为弹目初始距离;vc为接近速度，近似为(vP+vE)。剩余飞行时间可表示为

tgo=tf-t.

(7)

2　自适应滑模制导律

2.1系统降阶

基于式(5)求解零控脱靶量z(t)，z(t)表示拦截导弹和目标由给定的时间t起不施加任何控制，以该瞬时参数飞行，至命中时所产生的脱靶量，也即式(5)的奇次解。所求解的z(t)可表示为

z(t)=κ(t)x(t),

(8)

式中：

(9)

对式(8)两边关于时间t求导，可以得到：

(10)

式中：

(11)

(12)

原系统(5)被降阶为以零控脱靶量作为变量的标量形式。文献[9]基于对最优控制理论的分析，给出了相似的变换过程，称为终端投射变换(terminal projection transformation)。

2.2滑模制导律推导

式(10)中包含目标控制量部分uEc，是未知的，因此在制导律的执行过程中需要对这一量进行在线估计。无论采用何种滤波方式，估计结果却总是存在误差和延迟的，从而影响最终的脱靶量。本文设计了一种自适应滑模制导律，与目标信息滤波器集成使用以增强对估计误差的鲁棒性。

基于降阶后的状态方程(10)进行自适应滑模制导律的推导。由于z(tf)=y(tf)，所以选取零控脱靶量z(t)作为滑模面可以实现零脱靶量。定义滑模面：

s=z(t).

(13)

由于目标控制量uEc及其估计误差总是有界的，基于滑模控制方法，将其当作有界干扰对待，并且取其界值为Δ。定义Lyapunov函数：

(14)

对式(14)两边关于时间t求导，并结合式(10)可以得到：

(15)

选取控制量和自适应律：

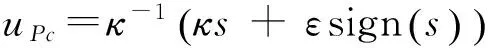
(16)

(17)

(18)

(19)

(20)

式(19),(20)和(8)即构成了所设计的高阶控制自适应滑模制导律(high-order control adaptive sliding-mode guidance law, HOASM)。该制导律设计中既考虑到了目标加速度及其估计误差的影响，因此对这2种干扰都具有较强的鲁棒性，同时由于采用了自适应设计，避免了对干扰或误差上界Δ保守估计所带来的制导性能损失。

3　滤波器设计

假设拦截导弹和目标具有相互独立的过程噪声且符合高斯分布，均值为0，标准方差分别为σP和σE。结合图1，采用一定的弹上量测设备可对弹目距离r、视线角q和导弹横向加速度aP进行量测。假设r是可精确量测的，q和aP具有一定的量测噪声，并且假设噪声为白噪声且符合高斯分布，标准方差分别为σq和σap。量测方程表示为

(21)

由于考虑非完全信息情形，主要应用成型滤波器(shaping filter, SF)表示目标的随机机动策略，采用任意且不局限于白噪声的随机输入驱动整个系统，进而实现系统的扩展。扩展后的系统，包括原系统和一个SF，与原系统具有相同的一阶矩和二阶矩。基于式(5)，经过扩展后的系统状态方程可以表示为

(22)

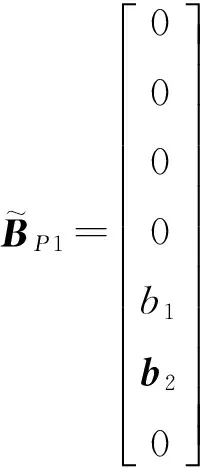
4　仿真结果及分析

[10-12]，假设拦截导弹和目标具有一阶控制系统动态，则零控脱靶量可表示为

(23)

ψ(α)=exp(α)+α-1，

(24)

式中：τP和τE分别为拦截导弹和目标的控制系统时间常数。结合式(10)，可以得到

κP=τPψ(tgo/τP)，

(25)

κE=τEψ(tgo/τE)，

(26)

用于制导律(19)和自适应律(20)的执行。

滤波器量测方程(21)和状态方程(22)可表示为

(27)

(28)

式中：

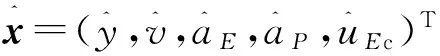
如图1所示，针对一类末端迎面拦截情形进行了仿真研究，仿真框图如图2所示，假设目标机动为具有一次时间切换的“bang-bang”类型[10]，γP(0)≈0,γE(0)≈0，其他仿真参数如表1所示。仿真结果如图3～6所示。

图2　仿真框图Fig.2　Simulation block diagram

表1　仿真参数

Table 1　Simulation parameter

参数值导弹飞行速度vP/(m·s-1)1200目标飞行速度vE/(m·s-1)800导弹控制系统时间常数τP/s0.2目标控制系统时间常数τE/s0.2导弹最大机动性能amaxP30g目标最大机动性能amaxE10g弹目初始距离r0/m6000过程噪声σP,σE0.1g,1g量测噪声σq,σap1mrad,0.1g

Kalman滤波器可以实现估计误差的均方根最小，能够随着噪声的大小进行带宽的自适应调整，然而当状态变量发生切变时，例如“bang-bang”目标机动[13]，这一变量的估计误差会变大，需要一定的时间才能够收敛到新值，即存在估计延迟，如图3所示为tsw=1.5 s时的目标加速度估计结果。图4和图5分别为采用所设计的自适应滑模制导律和最优制导律的脱靶量变化曲线和导弹加速度变化曲线，相应的脱靶量为0.21 m和1.30 m。

图3　目标加速度估计Fig.3　Estimation of target acceleration

图4　脱靶量Fig.4　Miss distance

图5　导弹加速度Fig.5　Missile accelerations

图6为所设计的高阶控制导弹自适应滑模制导律(HOASM)和最优制导律[14](optimal guidance law, OPG)的制导性能统计比较。仿真中两者取相同的目标机动命令切换时间tsw和随机数产生器种子，采用单发命中概率[12, 15]作为衡量指标，Monte Carlo仿真次数为500次。从图6中可以看出，由于增强了对目标估计误差的鲁棒性，HOASM制导性能优于OPG。当滤波器具有足够收敛时间的情况下，滤波精度较高，OPG和HOASM的制导性能基本相当，但当收敛时间不足时，如制导尾端的目标机动命令切换，HOASM的鲁棒性则较强，性能较好。

图6　单发命中概率Fig.6　Single shoot kill probability

5　结束语

本文考虑拦截导弹和目标具有任意高阶控制的情形，设计了具有一般性的自适应滑模制导律和滤波器。滤波器提供制导律执行所需的估计信息，而自适应滑模制导律增强了对目标加速度及其估计误差的鲁棒性。仿真结果表明，该制导律相比于最优制导律具有较为明显的性能优势。

在制导律推导过程中，仅将滤波器的目标加速度及其估计误差考虑到制导律的设计当中，并未进一步考虑估计延迟的影响，还有待进一步的研究。

参考文献：

[1]SHINAR J, TIRETSKY V, OSHMAN Y. Integrated Estimation/ Guidance Design Approach for Improved Homing Against Randomly Maneuvering Targets[J]. Journal of Guidance, Control and Dynamics, 2007, 30(1): 154-161.

[2]SHINAR J, TIRETSKY V. Three-Dimensional Validation of an Integrated Estimation/Guidance Algorithm Against Randomly Maneuvering Target[J]. Journal of Guidance, Control and Dynamics, 2009, 32(3): 1034-1038.

[3]ZHOU Di, MU Chun-di, XU Wen-li. Adaptive Sliding-Mode Guidance of a Homing Missile[J]. Journal of Guidance, Control and Dynamics, 1999, 22 (4): 589-594.

[4]ZHOU Jun, WANG Ting. Integrated Guidance Control System for Beam-Riding Guidance Missiles Based on Second Order Sliding Mode Control[J].Journal of Astronautics, 2007, 28(6): 1632-1637.

[5]BRIERLEY S D, LONGCHAMP R. Application of Sliding-Mode Control to Air-Air Interception Problem[J].IEEE Transactions on Aerospace and Electronic Systems, 1990, 26(2): 306-325.

[6]MOON J, KIM Y. Design of Missile Guidance Law via Variable Structure Control[J]. Journal of Guidance, Control, and Dynamics, 2001, 24(4): 659-664.

[7]花文华, 陈兴林. 前向拦截自适应滑模制导律[J]. 哈尔滨工业大学学报, 2011, 43(11): 30-33.

HUA Wen-hua, CHEN Xing-lin. Adaptive Sliding-Mode Guidance Law for Head Pursuit[J]. Journal of Harbin Institute of Technology, 2011, 43(11): 30-33.

[8]花文华, 陈兴林. 自适应二阶滑模制导律[J].现代防御技术，2011, 39(6):121-125,143.

HUA Wen-hua, CHEN Xing-lin. Self-Adaptive Second Order Sliding-Mode Guidance Law[J].Modern Defence Technology，2011, 39(6):121-125,143.

[9]BRYSON Jr A E, HO Y C. Applied Optimal Control: Optimization, Estimation and Control[M]. Waltham, MA: Blaisdell, 1969：148-176.

[10]SHINAR J, SHIMA T. Nonorthodox Guidance Law Development Approach for Intercepting Maneuvering Targets[J]. Journal of Guidance, Control and Dynamics, 2002, 25(4): 658-666.

[11]花文华, 孟庆龄. 寻的导弹范数型微分对策制导律[J]. 高技术通讯, 2013, 23(4):392-399.

HUA Wen-hua, MENG Qing-ling. Norm Differential Game Guidance Laws for Homing Missiles[J].Chinese High Technology Letters, 2013, 23(4):392-399.

[12]花文华, 孟庆龄. 有界控制导弹随机最优制导律[J]. 固体火箭技术, 2015, 38(1):7-11,17.

HUA Wen-hua, MENG Qing-ling. Stochastic Optimal Guidance Law for Bounded-Control Missiles[J].Journal of Solid Rocket Technology, 2015, 38(1):7-11,17.

[13]SHINAR J, STEINBERG D. Analysis of Optimal Evasive Maneuvers Based on a Linearized Two-Dimensional Kinematic Model[J]. Journal of Aircraft, 1977, 14(8): 795-802.

[14]赵善友. 防空导弹武器寻的制导控制系统设计[M]. 北京：中国宇航出版社, 1992:315-319.

ZHAO Shan-you. Antiaircraft Missiles Weapons Homing Guidance Control System Design[M].Beijing:China Aerospace Press, 1992:315-319.

[15]SHAFERMAN V, SHIMA T. Cooperative Multiple Model Adaptive Guidance for an Aircraft Defending Missile[C]∥ AIAA Guidance, Navigation, and Control Conference, Toronto, Canada: AIAA Press, 2010: 1-22.

Adaptive Sliding-Mode Guidance Law for High-Order Controlled Missiles

HUA Wen-hua1, MENG Qing-ling2, ZHANG Jin-peng1，2

(1. China Airborne Missile Academy,Henan Luoyang 471009, China；2. Aviation Key Laboratory of Science and Technology on Airborne Guided Weapons, Henan Luoyang 471009, China)

In order to improve guidance performance and robustness of the estimation error of target information, an approach of integrated filter and adaptive sliding-mode guidance law is presented. The filter provides necessary information for the guidance law, such as target acceleration et al, and the adaptive sliding-mode guidance law improves robustness of the estimation error of target information. Adaptive control method is introduced to guidance law design which can avoid guidance performance lost from conservative estimation of system disturbances or errors bounds. The filter and sliding-mode guidance law are deduced in general form and are adapted to interception missile and target with high-order linear control dynamics. Based on Monte Carlo method, simulations are carried out and the results show that as compared to optimal guidance law, the proposed approach has better guidance performance and improved robustness.

guidance law; sliding-mode control; high-order control; adaptive control; filter estimation error; Monter Carlo simulation

2015-08-12；

2015-11-13

航空科学基金资助项目(2015ZC12006)

花文华(1983-)，男，安徽淮北人。高工，博士，主要研究方向为飞行器制导与控制。

通信地址：471009河南省洛阳市030信箱5分箱E-mail：huawh6611@163.com

10.3969/j.issn.1009-086x.2016.04.006

TJ765.3

A

1009-086X(2016)-04-0031-06