基于RLS90模型与Kriging插值的城市交通道路噪声预测

周强波 徐翰

摘要[目的]为建立道路交通噪声预测和应用系统提供基础数据。[方法]运用GIS空间分析中的Kriging插值方法与RLS90模型相结合对城市交通道路噪声进行模拟预测，通过RLS90模型的声源模型与声传模型计算道路噪声值，运用Kriging插值方法进行空间模拟，对道路噪音未知样点进行线性无偏最优预测，并以湖南省长沙市芙蓉区雍景园典型小区为例，进行了验证。[结果]实例应用结果表明，长沙市芙蓉区雍景园小区5个测量地点的噪声预测值（67.40 dB）与测量值（66.26 dB）的空间分布和传播趋于一致。[结论] Kriging插值方法与RLS90模型相结合可以运用于道路交通噪声的實时预测和决策。

关键词Kriging插值；RLS90模型；道路噪声预测

中图分类号S181文献标识码A文章编号0517-6611（2016）04-103-03

Predictive Analysis of Traffic Noise in Urban Roads Based on RLS90 Model and Kriging Interpolation

——A Case of a Given Community in Furong District， Changsha City， Hunan Province

ZHOU Qiangbo， XU Han （230 Institute of Nuclear Industry， Changsha， Hunan 410007）

Abstract[Objective] To provide basic data for the prediction and application system of traffic noise in roads. [Method] Simulating prediction of traffic noise in urban roads was carried out by Kriging interpolation method and RLS90 model in GIS spatial analysis. Road noise value was calculated by sound source model and sound transmission model in RLS90 model； spatial simulation was carried out by Kriging interpolation method； linear unbiased prediction was adopted by the unknown sample sites of road noise. With a given community in Furong District， Changsha City， Hunan Province as an example， verification test was carried out. [Result] Spatial distribution and transmission of noise prediction value （67.40 dB） and measured values （66.26 dB） tended to be uniform in five measuring sites of Furong District. [Conclusion] Combining the Kriging interpolation method with RLS90 model can be applied in the prediction and decision making of road traffic noise.

Key wordsKriging interpolation； RLS90 model； Road traffic noise

近年来，随着城市汽车数量的急剧增加，导致城市交通噪声污染问题突出。目前，国内外对城市交通道路噪声监测开展的研究较多，如Glacier等[1]采用实际监测采样方法，对西班牙7个主要城市50个固定监测点进行长达20年的监测，得出一系列噪音分布图，并分析了西班牙主要城市交通噪声特征；英国的CRTN88模型适用于距离长、顺畅的高峰交通流，可以简单处理墙体对噪声反射的影响[2]；美国FHWA模型主要用于高速公路匀速车流的交通噪声预测，但未考虑道路坡度、路面性质、气象条件以及多重反射对噪声交通中断对噪声值的影响[3]；我国公布的GB17247.21998《声学 户外声传播的衰减第2部分：一般计算方法》等效采用了上述国际标准，计算原理考虑了噪声的衰减、散射、反射、吸收等[3]。目前，我国学者较少结合前人研究结果运用空间插值方法模拟监测区域噪音数据研究。鉴于此，笔者根据RLS90模型在城市道路交通中的应用理论，运用RLS90两大子模型对道路实测噪音进行评估分析，利用地理空间分析中的Kriging插值技术对噪音数据进行模拟预测，旨在为城市交通路线规划提供辅助决策支持及科学技术手段。

1RLS90模型

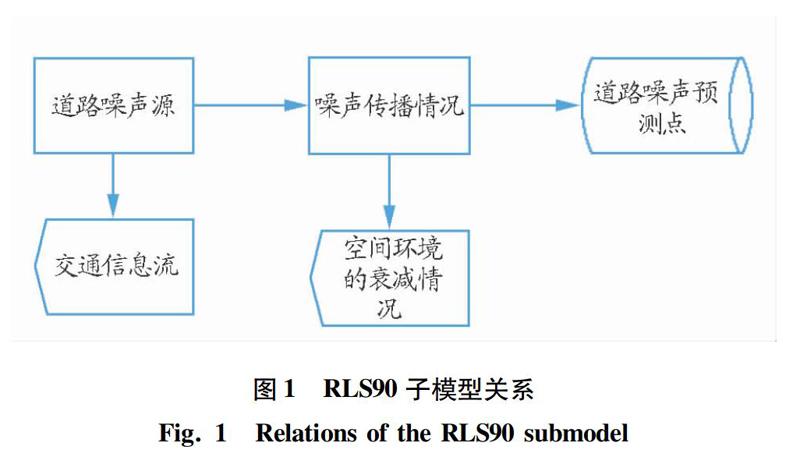
RLS90是对交通道路噪声进行预测分析的RLS81模型加以改进的一种模型。该模型以等效连续A声级LeqA为评价指标，包括声源模型和声传播模型2个子模型。模型构成关系如图1所示。

（1）对于一个街道的声级计算方法。

设预测点的噪声级Lr为：

Lr=Lm+K

式中，Lm为车道上计算噪声平均A声级；K为交通信号控制路口效果增加的一个额外量。

（2）对于长直线路段的计算方法。

对于每条线路，平均噪声级的计算公式：

Lm，i=Lm，E+Di+DS-DZ

Lm=10×lg100.1×Lm，i

式中，Lm，i为1条车道第i段平均声压级；Lm为车道上车辆行驶产生的噪声级；Lm，E为车道上车辆行驶产生的噪声级；主要与车道上的车流量、车型等数据有关；Di为不同小段的线声源长度修正值；DS为距离衰减修正值；DZ为遮挡物（建筑物或声屏障）衰减修正值。其中，车辆行驶产生的辐射噪声级计算公式：

Lm，E=Lm（25）+Dv+DStro+Dstg+Dmreft

式中，Lm（25）为距声源25 m，离地表4 m高处的平均A声级；Dv为速度调整因子；DStro为路面校正，范围为0～6 dB（A），一般沥青路面DStro=0，水泥混凝土DStro=2，多孔隙沥青混凝土DStro=-4或-5；Dstg为纵坡度修正值，当|g|>5%时，Dstg=0.6|g|-3；当|g|<5%时，Dstg=0；Dmreft为反射音修正值。

Lm（25）=37.3+101 g[M（1+0.082P）]

式中，M为单车道道路小时平均车流量；P为重型车比例。

Dmreft=4×HB/W≤3.2（反射面为非吸音介质）

Dmreft=2×HB/W≤1.6（反射面具有吸音性质）

式中，HB为反射面平均高度；W为声源至反射面距离。

Di计算方法：Di=101 g（i）。

DS计算方法：DS=11.2-20×lg（S）-S/200，式中，S为声源至接收点距离。

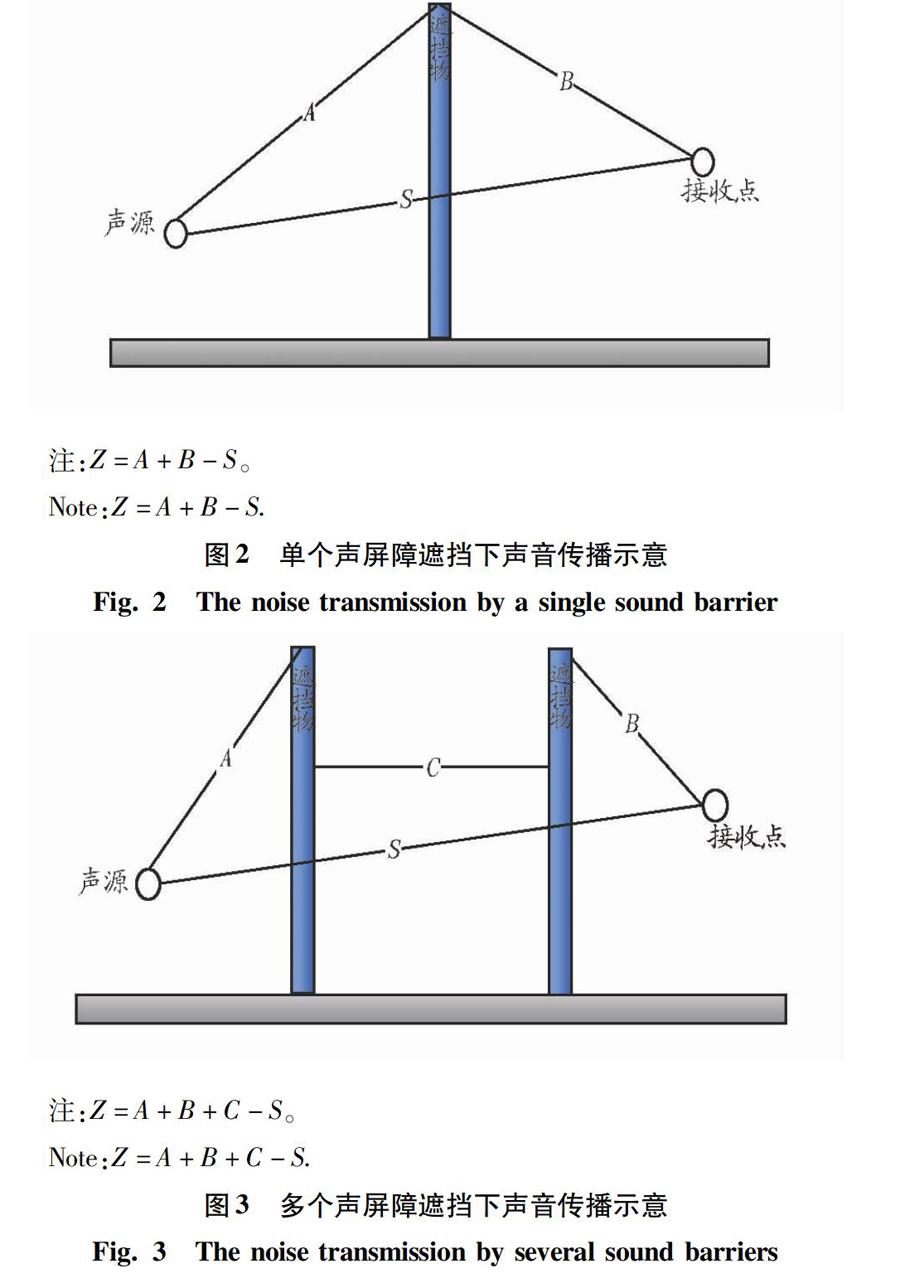
DZ的衰减正值计算方法：DZ=10×lg（3+80×Z×KW），式中，Z为绕射声传播路径（声源经遮挡物顶端至接受点）的长度与直达声传播路径（声源至接收点的直线距离）的长度间的差值。当只有1个声屏障时，如图2所示；当存在2个或2个以上声屏障时，如图3所示。

2关键技术

笔者重点探讨城市道路交通噪声模拟预测的准确性及对环境的影响程度，选择在RLS90交通噪声预测模型的基础上，根据实际研究区域情况实现城市交通噪声的Kriging插值预测道路噪音情况。技术模型如图4所示。

2.1声源模型计算RLS90模型对于声源模型计算的技术方法是当路段符合长直线的条件时，可采用声源模型进行计算，否则应采用声传模型进行计算。该模型的关键技术在于确定能够对预测点噪声有影响的街道（即线性声源），并计算声源产生的噪声强度。线性声源产生的噪声污染主要采用道路长度、宽度、材质、坡度、车流量、重型车比、车速、隔音墙等数据进行计算。

2.2声传模型计算声音在传播过程中会有损失，到达预测点的声音强度并不完全等同于声源点处的dB值。削弱声音的因素主要有建筑物、绿地、河流等可以吸收阻挡声音传播的地物。鉴于这些因素，笔者计算出线声源的每一微分弧段到预测点的噪声大小，最后进行叠加得到预测点处的总噪声值，再将离散点的噪声值内插得到整个区域面的噪声分布情况（图5）。

2.3内插技术输出噪声值克里金插值法是应用随机函数理论，不仅考虑待估点与已知点的位置相关程度，还考虑他们之间的空间相关性，对每个样点赋予不同权重，进行滑动加权平均，进而估算所求点的值[4]。克里金插值法的适用范围为区域化变量存在空间相关性，即如果变异函数和结构分析的结果表明区域化变量存在空间相关性，则可以利用克里金插值技术进行内插或外推；反之，不可行。

城市道路噪音预测点是根据未知样点有限邻域内的若干已知样本点数据，在考虑了预测区域实际测量样本点的形状、大小和空间方位，与未知样点的相互空间位置关系，以及变异函数提供的结构信息之后，对道路噪音未知样点进行的一种线性无偏最优预测估计。因此，选择克里金内插技术输出噪音预测结果。

其基本思路：设x1，…，xn为道路噪音预测区域的一系列实际观测点，z（x1），…，z（xn）为相应的观测值。区域化变量在x0处的值z×（x0）可采用一个线性组合进行估计：

z×（x0）=ni=1λiz（xi）

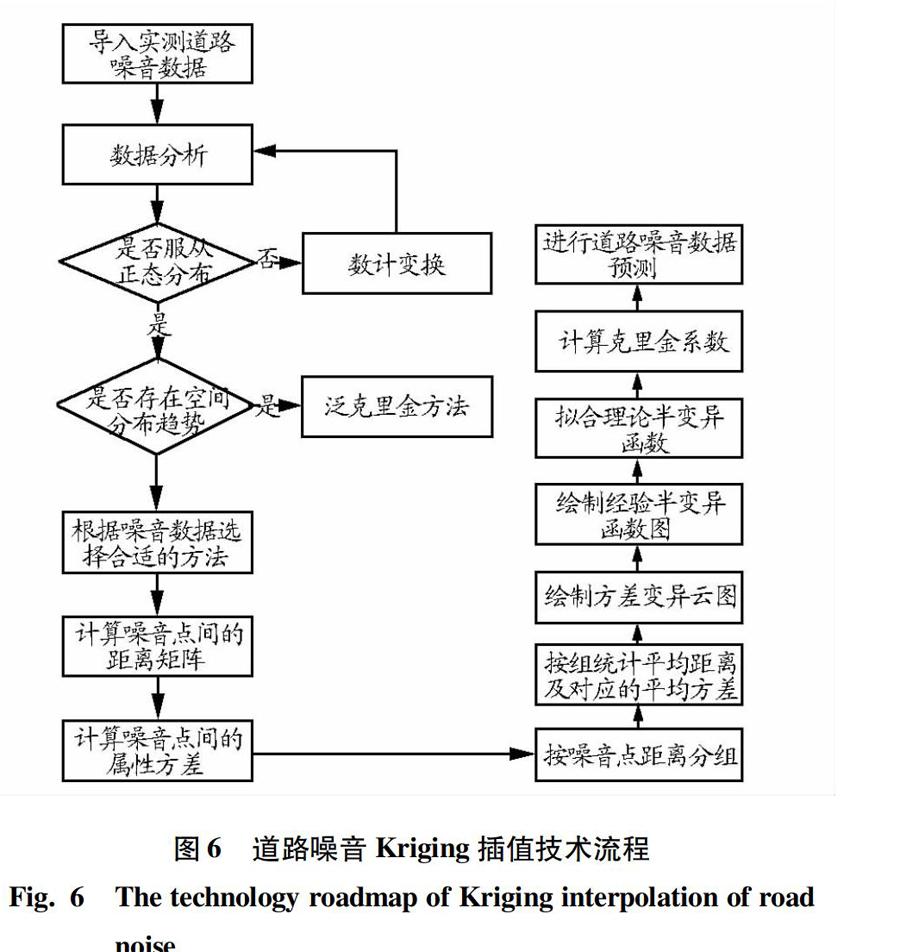
式中，z×（xi）为未知样点的值；z（xi）为未知样点周围的已知样本点的值；λi为待定加权系数；n为已知样本点的个数。道路噪音Kriging插值方法的技术如图6所示。

3实例应用

应用GIS与RLS90模型相结合构成的道路交通噪声预测模块对长沙市芙蓉区雍景园典型小区道路进行试验，该小区西临车站北路，北依雍景街，东接湘湖路，南靠晚报大道。采用的地理空间数据有研究区域1∶10 000 DEM数据、1∶500矢量基础地理数据资料和高分辨率遥感影像；噪声源属性数据有车流量、车速、轻重车型比和路面材料；影响噪声传播数据有建筑、声屏障和植被。预测点为高于地面1.5 m，距离反应物的距离至少为2.8 m，实测值测量的是距地表1.5 m的噪声值，噪聲预测结果比实际结果偏高。试验区5个测量点的预测值与测量值见表1，结果表明，噪声空间分布和传播趋于一致。

4结语

运用GIS技术与RLS90模型结合预测城市道路噪音值，充分利用GIS可视化和空间插值方法显示了道路噪声预测结果，两者结合的道路噪声预测值与实际测量值在空间分布和传播趋于一致。通过预测点的不同高度可以发现，道路噪声分布不仅具有水平面的空间分布，还有垂直面分布。然而，笔者仅仅是运用某一GIS空间分析技术与RLS90模型结合得出道路噪声预测值，而噪声分布不仅具有水平面的空间分布与垂直面分布，因此，结合实时空间预测，实现噪声的三维实时动态分布规律将是今后的研究方向。

参考文献

[1] GARCIA A，FAUS L J.Statistical analysis of noise levels in urban areas[J].Applied acoustics，1991，34：227-247.

[2] 李本纲，陶澍.应用英国CRTN88模式和GIS进行道路交通噪声预测与规划[J].环境工程，1999，17（5）：61-64.

[3] 邓佳，赵剑强，张晓宁，等.公路交通噪声预测模型FHWA与RLS90的比较[J].环境工程学报，2012（2）：687-691.

[4] 周汝良，丁琨，石雷.稀疏观测数据的空间内插方法的分析与比较[J].云南地理环境研究，2008，20（4）：1-4.44