类比地学联系地学

范建兵

类比地学联系地学

范建兵

类比是学习数学的一种重要的思维方法，“全等三角形”这一章内容里又有哪些类比思想呢？首先，请同学们思考这样一道题目：

图1

例1已知，如图1，以△ABC的边AB、AC为边分别向外作等边△ABD和等边△ACE，BE、DC相交于点O，求证：

（1）BE=DC；（2）∠DOB=60°.

【解析】由于△ABD和△ACE都是等边三角形，所以AB=AD，AE=AC，∠DAB=∠EAC=60°，所以∠BAE=∠DAC，由“SAS”定理可得△BAE≌△DAC，所以BE=DC，∠EBA=∠CDA，再由“8”字形结论可得∠DOB=∠DAB=60°.

这主要考查三角形全等的一种判定方法，条件明显，难度不大，大部分同学能够顺利证明两个结论.下面，再请同学们观察以下两题：

图2

例2已知，如图2，以△ABC的边AB、AC为边分别向外作等腰直角△ABD和等腰直角△ACE，BE、DC相交于点O，求证：（1）BE=DC；（2）BE⊥DC.

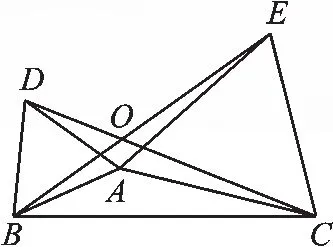
图3

例3已知，如图3，以△ABC的边AB、AC为边分别向外作△ABD和△ACE，且AD=AB，AE=AC，∠BAD=∠EAC=α，BE、DC相交于点O，求证：（1）BE=DC；（2）∠DOB=α.

如何解决这两道问题呢？请同学们仔细观察三个题目，并思考：

（1）从条件出发，三道题目有哪些异同点？

（2）从结论出发，三道题目有哪些异同点？

（3）从解题思路出发，解答例2、例3时能否类比例1的解题思路进行思考？它们之间有什么联系？

如果你能够回答上述三个问题，我相信你一定能够解答例2和例3.其实在我们学习全等三角形时，总会遇到一些像这样的“姊妹题”，或形似，或神似，只要我们能够透过现象看本质，不难发现，它们有众多的相通之处.

因此，同学们做几何习题时要常做常思，力争做一题带一类，培养解题感，提高学习效率.可以站在全局的角度，运用已有的数学知识，类比地学，联系地学，将陌生的问题与熟悉的问题进行类比，这样就可以更加系统地掌握数学知识.当然，在反思中，我还发现了一个小窍门噢，如果一道题目里出现两个等边三角形，或两个正方形，或两个等腰直角三角形，或两个等腰三角形，一般都会用“SAS”定理证明全等.

细心的同学，你同意我的观点吗？

（作者单位：江苏省苏州市学府中学）