大管径渐放管及焊接钢弯管局损系数简析

李　杰

（陕西省水利电力勘测设计研究院陕西西安710001）

大管径渐放管及焊接钢弯管局损系数简析

李杰

（陕西省水利电力勘测设计研究院陕西西安710001）

本文运用数学分析的方法，得出焊接钢弯管的管径与局部水头损失系数之间存在显著的对数相关关系；渐放管的d/D和（D/2）1/6与局部水头损失系数之间存在显著的多元回归关系。从而较好地解决了困扰设计者的大管径焊接钢弯管及渐放管的局部水头损失系数的取值问题，对水利工程设计具有较强的实用价值。

大管径渐放管；焊接钢弯管；局部水头损失系数；相关性分析

管道被广泛应用于给水、排水、供热、供煤气、长距离输送石油和天然气、农业灌溉、水利工程及各种工业装置中。大中型引调水工程常常会用到大管径的管道进行输水，管道难免会在局部有转弯或变径现象。水利工程中管道转弯处常常采用钢管现场焊接，在对焊接弯管和渐放管进行局部水头损失计算时，需要这些水力突变部分的局部水头损失系数，但目前接触到的相关工具书只给出管径1m以内的水头损失系数值。管径大于1m时这两种局损系数如何取值，成为困扰设计者的一道难题。本文在前人实验数据及经验总结所得数据基础上，运用数学计算的方法对机电灌排设计手册［1］中焊接钢弯管及渐放管在管径大于1m时的局部水头损失系数进行了研究，拟合出了精度较高的计算公式。

1　焊接弯管局损系数简析

1.145°焊接弯管局损系数

笔者以设计工作中遇到的实际问题为依托，查阅了大量的工具书及相关规范，其中机电灌排设计手册［1］给出了一系列DN1000以内45°焊接弯管的ζ值如表1所示。

经笔者分析，以D为自变量，ζ为因变量对表1中数值进行拟合，可得到两变量间存在较好的对数相关关系，如图1示。

两变量的相关关系如式1-1示：

式中，ζ——局部水头损失系数；

D——管道公称直径，mm；

R——复相关系数。

表1中16组数据的变量个数为2（自变量D，因变量ζ），自由度为14（16－2=14），查试验设计与分析［2］附表11可得R0.05=0.497，则R20.05=0.247＜R2=0.9507，即回归方程极显著地存在。

在同一管径下，对公式1-1计算所得ζ值如表2示，与表1中ζ值进行比较，其平均相对误差为3.5%，最大相对误差为8.7%。据此就可以对DN1000以上45°焊接弯管的ζ值进行延展计算，且可保证所计算数值的精度。

例如，对于我国北方某加压供水工程，其输水管道大部分采用DN2000PCCP管（较大拐点设镇墩处以焊接钢管代替）。管线某处有45°拐点，做泵站选型水力计算时，要用到此拐点的局部水头损失系数ζ，则ζ值可带入式1-1求得，过程如下式1-2所示：

ζ=0.10841n2000-0.1932=0.63（1-2）1.2 90°焊接弯管局损系数

同样，机电灌排设计手册［1］给出了一系列DN1000以内90°焊接钢弯管的ζ值，如表3所示。

经笔者分析，以D为自变量，ζ为因变量对表2数值进行拟合，可得到两变量间存在较好的对数相关关系，如图2示。

两变量的相关关系如式1-3示：

ζ=0.2181nD-0.3983 R2=0.9566（1-3）式中，ζ——局部水头损失系数；D——管道公称直径，mm；R—复相关系数。

表3中16组数据的变量个数为2（自变量D，因变量ζ），自由度为14（16－2=14），查试验设计与分析［2］附表11可得R0.05=0.497，则R20.05=0.247＜R2=0.9566，即回归方程极显著地存在。

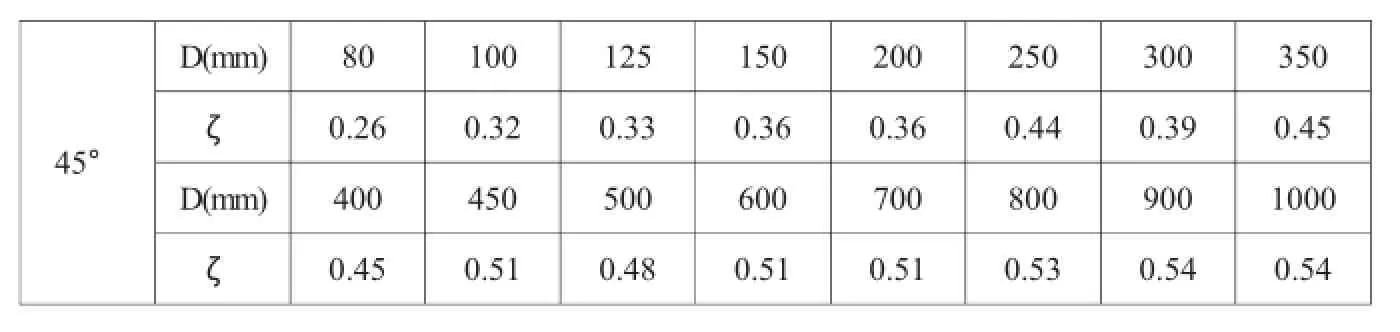
表1　DN1000以内45°焊接弯管ζ

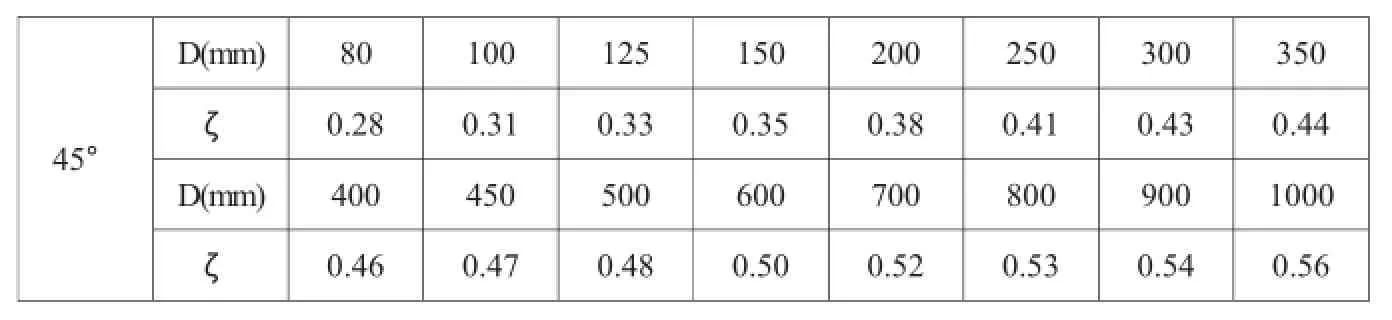
表2　DN1000以内45°焊接弯管公式1-1计算ζ

图145　°焊接弯管D～ζ曲线图

在同一管径下，对公式1-3计算所得ζ值如表4所示，与表3中ζ值进行比较，其平均相对误差为3.4%，最大相对误差为8.4%。据此就可以对DN1000以上90°焊接弯管的ζ值进行延展计算，且可保证所计算数值的精度。

至此，我们就分别得到了45°与90°焊接钢弯管管径D与对应局部水头损失系数ζ的数学拟合公式。后续相关水利工程设计过程中，在进行水头损失计算时，对于直径大于1m的0°～180°的任意角度焊接钢弯管，就可以分别计算出45°和90°对应的ζ值，然后运用内插或外插的方法计算出所需角度的ζ值。

例如，目前正在施工的延安黄河引水工程，是以黄河为主要取水水源的长距离引水工程。工程建设目的是解决延安市及周边县区的长期缺水问题，属延安市“十二五”重点水利基础设施建设项目。工程年供水总量为8977万m3/a，最大引水流量为4.2m3/s，通过5级泵站加压，约84km管线输水至延安市东川水厂及沿途各受水点。该工程建成投运后可解决沿线及延安市约70.56万人城镇居民生活用水、并为该地区工业生产用水提供可靠保障。

延水关二级泵站为该工程5级泵站中的第二级，泵站设计流量为4.1m3/s，设计扬程为66m，泵站厂区内泵后输水干管为DN1600的钢管，厂区2#镇墩处钢管转角的圆心角为32°52′49″，在进行泵站选型计算时就要知道该弯管的局部水头损失系数ζ值。此值即可将管道公称直径1600mm，分别代入到本文公式1-1和1-3，求得圆心角分别为45°和90°时该管径下焊接钢弯管的ζ值分别为：ζ45°=0.61，ζ90°=1.21。

则运用等比公式可外插得到圆心角为32°52′49″时焊接钢弯管的ζ=0.44，管道通过设计流量4.1m3/s时，对应的流速V=2.04m/s，则水流通过上述弯管时的局部水头损失为：

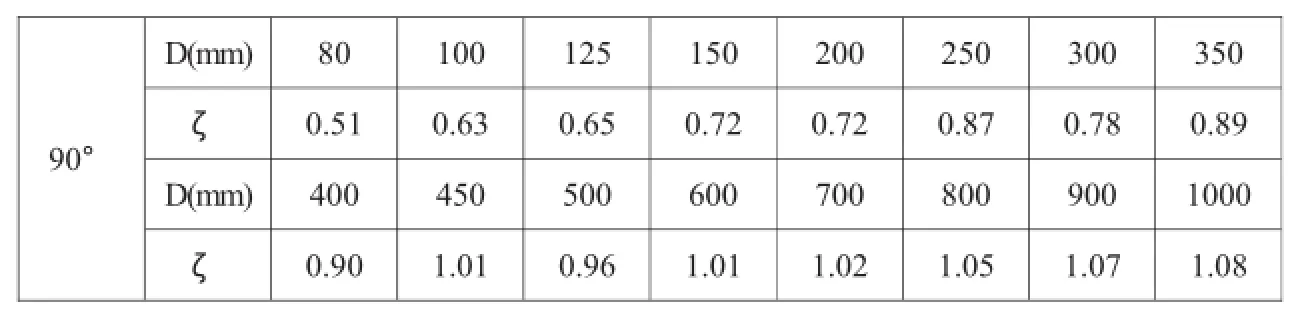
表3　DN1000以内90°焊接弯管ζ

表4　DN1000以内90°焊接弯管公式1-3计算ζ

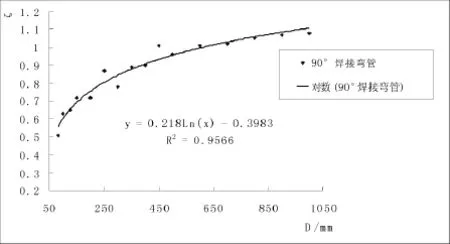
图290　°焊接弯管D～ζ曲线图

2　渐放管局损系数简析

机电灌排设计手册［1］给出了DN1000以内不同管径组合下渐放管（图3所示）的ζ值，如表5示。

经分析研究，得出渐放管的局部水头损失系数ζ值与d/D及（D/2）1/6之间存在相关关系。以d/D和（D/2）1/6两值为自变量，以ζ为因变量，用多元回归分析的方法分析可以得到三变量之间的相关关系如式1-5示。

式中，d/D——小管径与大管径之比值；

D/2——大管径的水力半径，m；R——复相关系数。

表5　DN1000以内渐放管ζ

表6　DN1000以内渐放管公式1-5计算ζ

图3　渐放管示意图

表5中52组数据的变量个数为3，自由度为49（52－3=49），查试验设计与分析［2］附表11可得R0.05=0.339，则R20.05=0.115＜R2=0. 9392，即回归方程极显著地存在。将表5中相关数据代入公式1-5可得到一系列数据如表6示。对表5及表6中数据进行比较计算，可得其平均相对误差为10.6%，且误差主要由d/D＞0.8的系列值引起，d/D≤0.8时平均相对误差为6.3%，可满足数值计算的精度要求。

仍以延水关二级泵站为例，泵后0#镇墩处布设有DN1400～DN1600的渐放管，水力计算时用到的局部水头损失系数ζ值可由d及D值代入式1-5求得，过程如下：ζ=0.015678-0.65105（1.4/1.6）+0.787416（1.6/2）1/6=0.20

3　结语

管道以其施工便利，占地少，寿命长的特点被广泛应用于引调水工程。如果把管道比作构筑起引调水工程的动脉，则泵站就是引调水工程的心脏，水泵又是泵站的心脏。只有通过精确的水力计算才能帮助设计者选到合适的水泵，才能做到精准化设计，水利工程也才能更好的发挥其社会经济效益。本文运用数学分析的方法较好地解决了困扰设计者的水力计算中大管径焊接钢弯管及渐放管的局部水头损失系数的取值问题。对水利工程，特别是引调水工程设计有很大的帮助，对水利工程更好的发挥其作用大有裨益。陕西水利

［1］皮积瑞，解广润.机电灌排设计手册［M］.北京：水利电力出版社，1992

［2］袁志发，贠海燕.试验设计与分析［M］.北京：中国农业出版社，2007

（责任编辑：畅妮）

TV134

A