基于矩形Packing问题求解的页面自动排版方法

李治江，崔广勋，王嵩

1.武汉大学印刷与包装系，湖北武汉430079

2.高德软件有限公司数据研发中心，北京102200

基于矩形Packing问题求解的页面自动排版方法

李治江1，崔广勋1，王嵩2

1.武汉大学印刷与包装系，湖北武汉430079

2.高德软件有限公司数据研发中心，北京102200

为了较好地实现页面的自动排版，本文提出了基于矩形Packing问题求解的页面自动排版方法。该方法采用结构化描述语言来分析描述版面的图文内容及排版样式，通过构建页面模型把页面自动排版问题抽象为关于图文混排矩形块的版面布局自动规划问题，根据矩形块面积排序，判断约束信息，定位步骤和回溯步骤，得到最终的页面自动排版效果。通过页面数据排版实验进行测试，实验验证该方法能较好地符合条件要求。

自动排版；矩形Packing

1　引言

随着互联网的发展，信息量的膨胀，电子设备的普及和环保无纸化观念的推广，网络出版以其效率更高、价位更低、检索快捷、避免绝版等优点不断冲击着传统出版市场，传统出版向网络出版转型是出版行业发展的趋势［1-3］，自动排版的实现将缩短排版工序用时，为出版行业带来产业化的效益提升。

近年来不少学者对排版问题进行了研究，取得了一些成绩［4-11］。如张金美介绍了CorelDRAW12在排版中的应用和技巧［4］；王勇等分析比较了LaTeX和方正书版2种软件排版数学论文的特点［5］；李金城等利用JavaScript在Indesign中实现基于XML结构化文档的自动排版［6］；肖建国等关注XML技术在跨媒体领域的应用［7-9］；苏勇的专利根据给定的固定栏数、栏距、页面区域面积等信息进行自动图文排版，不适用于页面含有多个信息块的复杂情况［10］；王罡等在图片排版中使用了模拟退火算法进行迭代优化［11］。针对矩形Packing NP完全问题的现实应用实例，还有许多学者也做出了相关研究［12-14］。现有的研究部分关注CorelDRAW、word等软件的排版，不具有普适性；部分关注图片或文字的单独排版，容易出现图文版面尺寸不匹配等问题，同时调整的影响面比较大，效率较低。受以上研究启发，本文对页面自动排版方法进行研究，提出一个基于矩形Packing问题求解的自动排版的算法。

2　页面模型

2.1基于矩形Packing问题的求解模型

矩形Packing问题是一类特殊的Packing问题，是面向货物装载、木材下料等现实应用的问题抽象。求解矩形Packing问题的常见优化算法主要包括遗传算法、模拟退火算法、动态规划与启发式算法等［15］。常见的矩形Packing问题有矩形背包、装填、布局问题［15］。自动排版问题与矩形块布局问题最为相似。

对页面元素进行结构化表达，可以将围绕某一主题的图文信息块抽象为矩形块，由此可得到n个矩形块Ri（i=1，2，...，n）。假设已知宽度为w高度为h的待排矩形版面区域R0，页面自动排版的目的是以矩形块面积为排序依据，根据面积大小进行定序，以不同填角动作的优度高低进行定位，将这n个矩形块互不重叠地放入待排矩形版面中。此问题可以形式化地描述为：将二维笛卡尔坐标系的原点取在待排区域的左上角，（0，h）为待排区域的左下角坐标，（w，0）为待排区域的右上角坐标，求n个四元组的集合，即

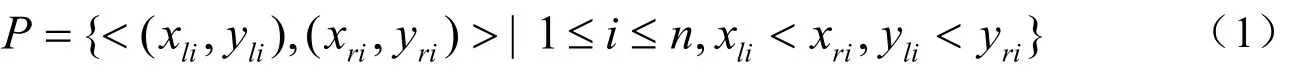
使这n个矩形块的最小外包矩形的面积最小，生成样式美观、留白均匀的页面。其中，（xli，yli）表示矩形块i的左上角坐标，（xri，yri）表示右下角坐标，且对于任意的矩形块i，其坐标满足如下条件约束：

（1）矩形块的每条边均与平面直角坐标系的x轴或y轴平行（或重合）；

（2）任意两矩形块互不重叠；

（3）任意矩形块均在待排区域内，即0≤xli＜xri＜w，并且0≤yli＜yri＜h。

2.2页面模型要素及操作定义

定义1（角区）由于本文探讨的是矩形图文信息块，因此两相邻矩形块所形成的夹角必为直角，角区即为两相邻矩形块与空白区域形成的直角范围，使用五元组表示：

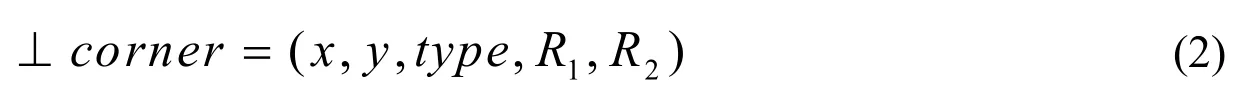
式中，x，y表示角区所处直角顶点的坐标，R1，R2表示直角两边所在的矩形块，角区的type共分为四种：└、┘、┌、┐。如图1所示a、b、c、d四个直角标注为各种角区情况。

图1　角区和填角动作Fig.1Cornerareas and action to fillthem

图2　一般填角动作的优度Fig.2Optimalaction to fill cornerareas

图3　面积权重的霍夫曼树构建Fig.3Construction of Huffman tree of area weight

定义2（填角动作）在某一布局之下，若放入的矩形块R与容器中已有矩形块（本文将初始版面定义为由页边距参数形成的四个矩形块包围而成的版心）中的某两块Ri和Rj的不同方向边有重叠，且重叠长度大于0，则矩形块R占据了由矩形块Ri和Rj形成的一个角区，此时称该矩形块的放入动作为一个填角动作。使用二元组（Corner，R）表示一个填角动作，表示将矩形块R填入Corner的角区。

如图1所示，现要将矩形块R3放入已放入R1R2R4R6的布局中（边界矩形为RTRBRLRR），当前布局共有7个角区。图中3-1的填角动作表示为（Corner1，R3），3-2为（Corner4，R3），3-3为（Corner5，R3），3-4为（Corner6，R3）。其中，合法填角动作为3-1、3-3、3-4。

定义3（合法填角动作的优度）对于一般填角动作（Corner，Ri），其优度γ计算表达式为：

式中，dmin为Ri与所有已填入当前布局的矩形块（包括构成排版区域的4块边界矩形块RTRBRLRR但不包括构成此角的矩形块RL和R2）距离中最小的，wi和hi分别为矩形块Ri的宽度和高度，如图2所示。

定义4（矩形块距离）给定矩形块Ri和Rj，其距离dij表达式为：

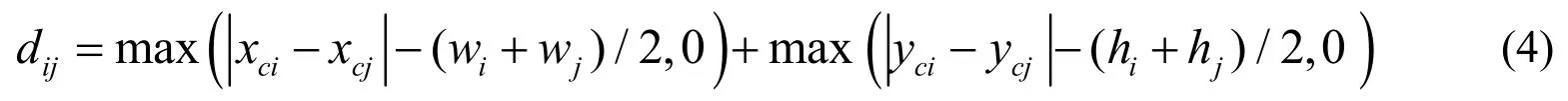
式中，（xci，yci）和（xcj，ycj）分别为矩形块Ri与Rj的中心点坐标；wi、wj分别为宽，hi、hj分别为高。

（1）矩形块内不分栏情况下，图片绕排方式为嵌入型时第i个矩形块面积Si表达式为：

式中，Nm表示正文字数，Nt表示标题字数，Iw表示图像宽度，Ih表示图像高度，Rd表示图像绕排间距。

（2）矩形块内分栏情况下，矩形块的面积分为最小占用面积Smin、最大占用面积Smax和平均占用面积，由栏宽很大程度决定，因此将矩形块面积表达式视为与分栏数ni相关的函数式Si=f（ni），其中

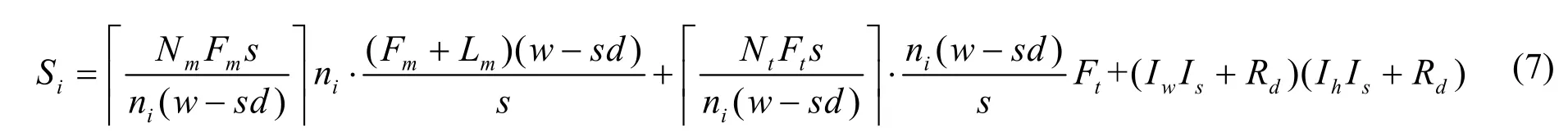
初始计算时，通过图文混排各条件参数的中值计算得到每个矩形块的近似折中面积S'i。再按下述公式（8）求得矩形块的近似面积Si。式中，S为初始页面待排区域面积，λ为权重调节因子，针对算法不同调节初始计算信息块面积占总面积的权重比。

定义6（霍夫曼树面积权重分级）在以面积作为节点权值构成的霍夫曼树中，我们根据叶子节点的起止深度定义其权重级别。如图3所示的霍夫曼树，S4与S1，在霍夫曼树中为第二层，在面积权重分级中则为第一级，S7、S2与S6为树的第三层，面积权重为第二级，S3与S5为树的第四层，面积权重为第三级。

3　页面自动布局的最优化求解

本文将页面中各矩形块描述为固定模板和可变数据两部分［16］，分别进行处理。定序过程中，先判断其约束信息，优先填入固定模板。此时，位置约束下的版面分割问题即可转化为一个初始布局为已在中间位置填入部分内容的一般版面布局自动规划问题，本文采用贪心算法进行最优化求解。

3.1基于霍夫曼树的版面分割

矩形块面积是页面局部优化过程中重要的决定参数，论文引入霍夫曼树模型对信息块面积进行带权分级。同时，本文将版面分割过程霍夫曼树模型进行关联对应，通过分割方向与分割比例参数控制所生成的版面，如图4图5所示，然后再使用二叉树进行表达，其表达效果如图3所示。

3.2基于贪心算法的最优化求解

基于贪心算法，本文采用限制条件约束的递归回溯算法，依照优先顺序逐个遍历尚未放入的矩形块，根据本文定义的操作，根据面积，优先放入角区，若有放置不下或是使全局留白均衡度超限的情况则进行回溯放置，直至所有矩形块全部放入。基本算法描述如下：

（1）在当前布局状态下，枚举出待排区域的所有合法填角动作；

（2）对于每个待排的矩形块，计算其所有的合法填角动作的优度；

（3）将优度最大的合法填角动作对应的矩形块放入待排区域内；

（4）更新当前布局，得到新的布局。

回溯过程是指在矩形块没有能够全部排入待排区域的情况下，进行回溯操作，具体步骤主要包括：

（1）选择排版步骤中合法填角动作的优度次之的角区进行填角动作；

（2）选择排入顺序优先度次之的矩块进行排入。

空白区合并的步骤为：

首先遍历空白区的各边，计算与之相邻的矩形的重叠边长，根据重叠比例及是否为端线进行优先级排序，并按优先级进行空白区并入。

4　实验与分析

对本文提出的方法，用如图6所示的测试数据进行测试。对于该待排的报纸版面，共有11个矩形块组成：其中矩形块S3、S5、S7是图片和文字一体的，S1、S2和S11分别代表报纸页面的报眼、头版和导读信息，具有位置约束信息，需要优先排入。由公式（6）和公式（7）计算的矩形块的分栏面积。

图4　待轴分版面Fig.4 Page layout waiting for partition by axis

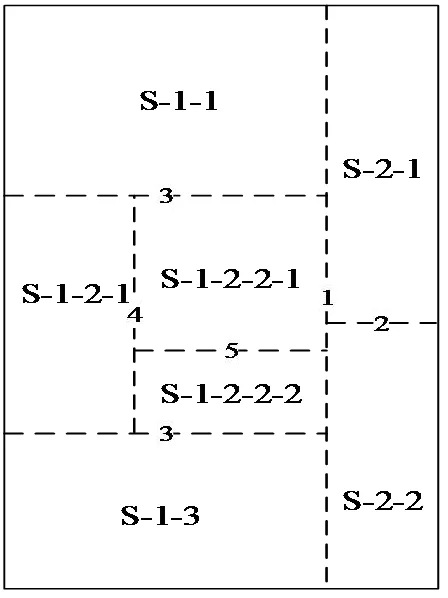
图5　轴分版面效果Fig.5 Effect of page layout parting by axis

图6　测试数据原始版面Fig.6 Initial page layout of test data

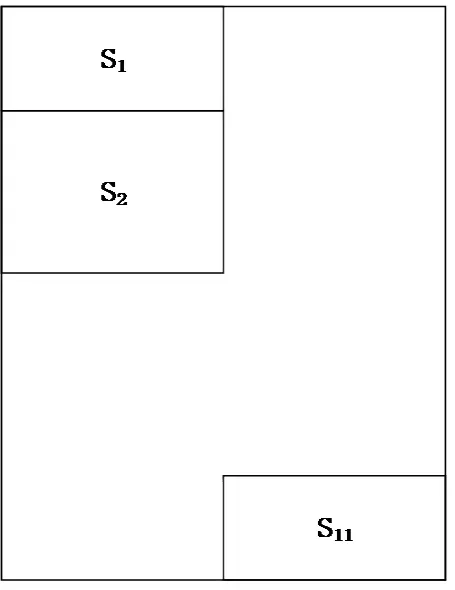
图7　位置约束Fig.7 Constraint location

图8　初始版面Fig.8 Initial page layout

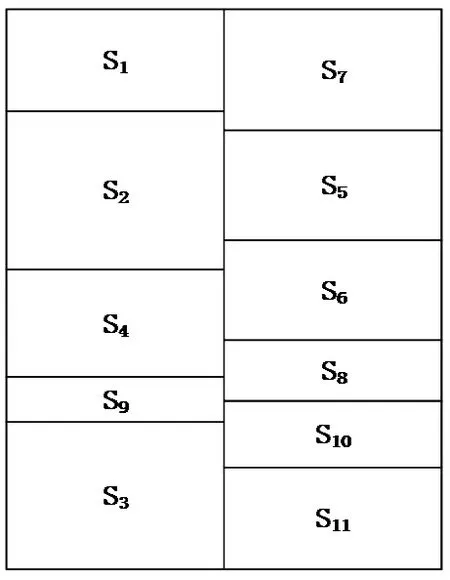
图9　空白区合并Fig.9 Merged blank areas

图10　最终布局结果Fig.10 The final page layout

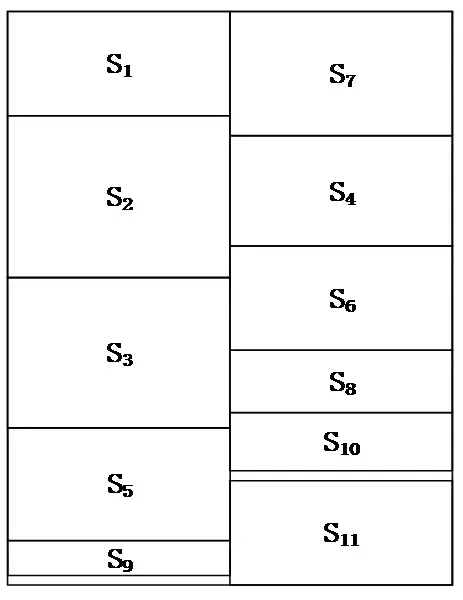
图11　GA布局结果Fig.11 GA page layout

表1　测试数据矩形块填入面积（mm2）Table 1 Areas of test data filled in rectangular blocks

为了验证本文方法，针对同一实验数据，采用遗传算法（Genetic algorithms，GA）进行了版面自动布局实验，实验结果如图11所示。根据实验结果，能够发现：

（1）GA算法的处理结果并没有考虑空白区合并的优化策略；

（2）本文方法采用的回溯策略能够更好地得到最优解。

（3）本文算法的时间复杂度为O（n*logn），GA的时间复杂度为O（T*n2），实验过程亦能验证本文方法的处理效率更优。

4　结语

本文仅对以矩形信息块构成的布局较为方正规整、留白较为均匀的版面自动排布问题进行讨论，对版面风格相对欢快，会有超出一般矩形块的表达方式，如倾斜矩形、梯形乃至不规则多边形等，暂未给出解决方案。该算法可以较好地应用于要求整版分栏线区分明显且无优先序的版面布局，也可应用于页面中有固定矩形块内容与位置关联的版面布局。

［1］程维红，任胜利，路文如，等.我国科技期刊由传统出版向数字出版转型的对策建议［J］.中国科技期刊研究，2011，22（4）：467-474

［2］肖洋.我国数字出版产业发展战略研究——基于产业结构、区域、阶段的视角［D］.南京：南京大学，2013

［3］齐福斌.数字出版与传统出版数字化转型［J］.印刷世界，2012（1）：4-10

［4］张金美.CorelDraw12在报纸排版设计中的应用［J］.硅谷，2014（21）：229，212

［5］王勇，姚萍，王岚，等.LaTeX与方正书版排版数学论文探讨［J］.中国科技期刊研究，2012，23（6）：1036-1039

［6］李金城，余方，方婷云.利用JavaScript编程在Indesign中实现基于XML结构化文档的自动排版［J］.中国科技期刊研究，2015（2）：172-175

［7］肖建国.XML和DAM技术与跨媒体出版［J］.印刷世界，2001（4）：6-7

［8］郭颖妤.XML在跨媒体出版中的应用［J］.印刷杂志，2004（11）：46-48

［9］Li Shuwei，You FuCheng.Research on XML Digital Signature Application in the Log Protection of Typesetting on Web.2012 International Conference on Control Engineering and Communication Technology，2012（15）：619-623

［10］苏勇.一种图文的自动排版方法：中国，200710121797.0［P］.2008-02-13

［11］王罡，彭国华，余迁.模拟退火算法在图片优化排版中的应用［J］.西南民族大学学报：自然科学版，2006（3）：586-590

［14］Hopper E，Turton B.An Empirical Investigation of Meta-heuristic and Heuristic Algorithm for a 2D Packing Problem［J］. European Journal of Operational Research，2001，128（1）：34-57

［15］周绍梅，赵苗，吴悦成.基于单亲遗传算法的最优布局问题求解［J］.计算机与现代化，2007（11）：40-42

［16］Jansen K，Solis-Oba R.Rectangle packing with one-dimensional resource augmentation［J］.Discrete Optimization，2009，6（3）：310-323

［16］陈端兵.求解矩形Packing问题的纯粹拟人算法［D］.武汉：华中科技大学，2007

［17］李治江，林武，王强.可变数据出版系统的设计与实现［J］.中国印刷与包装研究，2009（1）：75-80

Automatic Page Layout Based on Solution for Rectangular Packing Problem

LI Zhi-jiang1，CUI Guang-xun1，WANG Song2
1.Department of Printing and Packaging/Wuhan University，Wuhan 430079，China
2.Data Research and Development Center/AutoNavi Software Co.Ltd.，Beijing 102200，China

In order to realize automatic page layout，a method based on rectangular packing problem was proposed.It was described the graphics，texts and layout style of pages through the Structural language.The automatic page layout problem was formalized as a rectangle packing blocks with image-text contents to obtain the final automatic page layout effect according to sorting the areas of rectangles，judging constraint information，positioning each rectangles and backtracking algorithm.Experiment was carried out by using the page layout data and the result was able to well match the requirements.

Automatic page layout；rectangle Packing

TS812+.2

A

1000-2324（2016）02-0264-05

2015-04-03

2015-05-10

国家科技支撑计划：跨媒体数字出版平台标准及规范研究（2012BAH91F03）；武汉大学自主科研项目：基于多源数据融合快速检索（2042014gf013）

李治江（1977-），男，博士，副教授，研究方向为视觉分析与检测、数字出版技术.E-mail：lizhijiang@whu.edu.cn