衡重式挡土墙外倾对山区公路拓宽路基沉降的影响

蒋　鑫，陈　滔，吴　玉，朱奇炯，耿建宇，邱延峻

(1.西南交通大学 土木工程学院，四川 成都　610031；2.西南交通大学 道路工程四川省重点实验室，四川 成都　610031；3.西南交通大学 高速铁路线路工程教育部重点实验室，四川 成都　610031；4.上海铁路局 杭州工务段，浙江 杭州　310009；5.四川交投建设工程股份有限公司 桥梁与隧道工程分公司，四川 成都　610041)



衡重式挡土墙外倾对山区公路拓宽路基沉降的影响

蒋鑫1,2,3†，陈滔1,2,3，吴玉1,2,3，朱奇炯4，耿建宇5，邱延峻1,2,3

(1.西南交通大学 土木工程学院，四川 成都610031；2.西南交通大学 道路工程四川省重点实验室，四川 成都610031；3.西南交通大学 高速铁路线路工程教育部重点实验室，四川 成都610031；4.上海铁路局 杭州工务段，浙江 杭州310009；5.四川交投建设工程股份有限公司 桥梁与隧道工程分公司，四川 成都610041)

山区公路路基单侧拼接式拓宽改建多下设包括衡重式挡土墙在内的支挡建筑物于新路基外侧.运用Phase2有限元软件，引入Joint单元，构建可精细描述土-墙相互作用的数值模型，采用两步走、墙面施加非零位移约束方式模拟挡土墙平动加绕墙趾转动(RBT)主动外倾变位，分析挡土墙不同主动外倾变位量对新旧路基顶面差异沉降的影响，并与土工离心模型试验结果进行验证比较.结果表明：下设的刚性挡土墙与新老路基相互作用，共同依存.数值模拟反映当主动外倾量与墙高之比为1%～3%时，由挡土墙主动外倾变位产生的附加差异沉降占总差异沉降的51%～67%，此值明显低于土工离心模型试验结果.

山区公路；路基拓宽改建；挡土墙主动外倾变位；附加差异沉降；有限单元法

近年来，随着交通量剧增，我国西部山区公路路基拓宽改建工程日益增多，典型工程包括国道318线四川二郎山至康定段[1]、重庆市319国道新桥至山洞段[2]等.与平原软土地区有所不同，因傍山修建，山区公路路基拓宽多为单侧拼接式，且多下设包括衡重式挡土墙在内的刚性支挡建筑物，以避免过度放坡导致填方量过大.实际工程中，多见新老路基顶面出现差异沉降的同时，伴随着下设支挡建筑物的外倾变位，在此基础上，因各种原因，如墙底受水浸泡、冲刷，或墙体本身处于潜在滑坡体内，或挡土墙所受土压力过大等，导致支挡建筑物继续外倾变位，又将加剧新老路基顶面差异沉降，显然下设支挡建筑物与新老路基之间相互作用，共同依存.既有研究多集中于平原软土地区路基拓宽改建[3-7]，直接针对山区公路路基拓宽改建的深入研究尚不多见.廖军等[1]、廖敬梅等[8]、陆阳等[9]分别开展了支挡约束下拓宽道路不均匀沉降及挡土墙的变形与稳定现场监测；张家国[10]开展了山区公路路基拓宽中衡重式挡土墙的受力及变形特性的土工离心模型试验研究；万智等[11]采用有限元软件ANSYS，分析了山区拓宽公路挡土墙路基的受力与变形特征，重点探讨不同路基拓宽宽度、老路路堤边坡坡度及新路基填筑材料对路基拓宽的影响；耿建宇[12]采用有限元软件Plaxis，重点分析了加筋、压实状况等条件对新路基填筑导致下设衡重式挡土墙被动外倾的影响.

结合山区公路路基拓宽改建的特殊性，本文拟选用加拿大开发的有限元软件Phase2，对下设衡重式挡土墙的山区公路路基拓宽过程及挡土墙主动外倾变位对路基面沉降的影响开展数值模拟，明确新旧路基顶面由新路基填筑产生的初始差异沉降和挡土墙主动外倾变位产生的附加差异沉降在总差异沉降中各自的权重，并与既有土工离心模型试验成果验证比较，从而为山区公路路基拓宽改建工程沉降的准确计算奠定基础.

1　有限元数值模型构建

1.1模型几何尺寸与边界条件

[12]，假定为平面应变问题，图1给出了外设衡重式挡土墙的山区二级公路拓宽改建路基的有限元计算全结构数值分析模型.由原双向二车道拓宽至双向四车道，即由12 m宽原路基拓宽为22 m.新旧路基衔接面边坡坡度为1∶0.8，新路基外侧设置上、下墙高分别为4 m和6 m，总墙高10 m，上墙墙背仰斜坡度为1∶0.25，下墙墙背俯斜坡度为1∶0.25的衡重式挡土墙.新路基填高10 m.暂不考虑新旧路基衔接面台阶的设置，假设新旧路基衔接面接触良好，完全连续.模型的底侧为水平向及竖直向位移均约束，左右两侧为水平向位移约束，竖直向自由，以模拟在新路基荷载作用下的竖向压密.衡重式挡土墙底部的钢筋混凝土托梁、桩基及新路基内的土工格栅等均暂不考虑.模型中其余尺寸如图1所示.

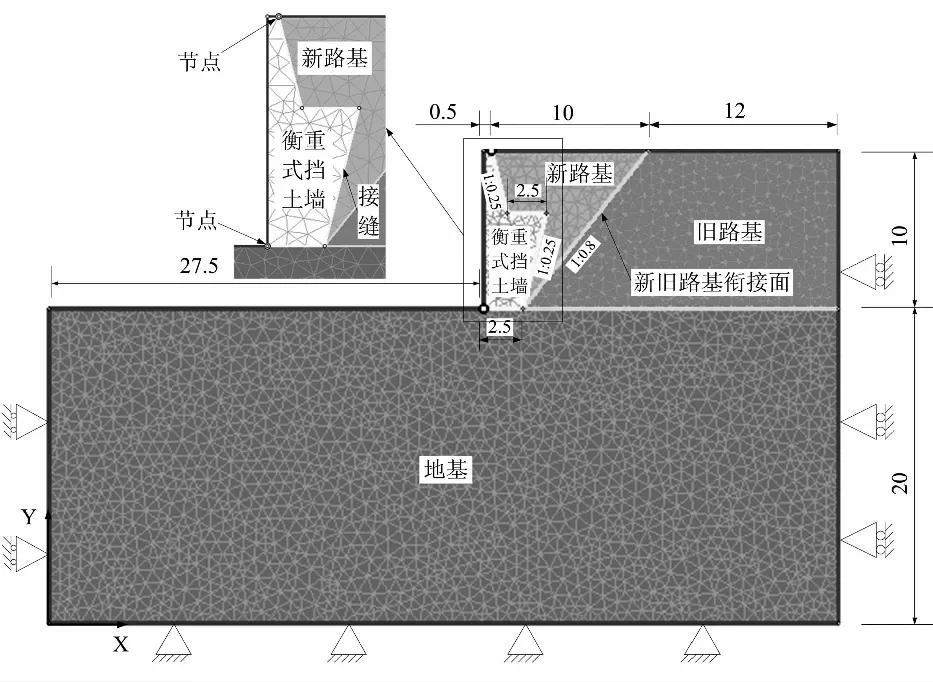
图1　有限元计算模型(未按比例，单位：m)

1.2本构模型及材料参数

模型中地基、旧路基和新路基均视为服从Mohr-Coulomb破坏准则的理想弹塑性材料，衡重式挡土墙视为理想线弹性体.考虑到旧路基系依山而建，不妨取旧路基和地基相同土体材料参数，参考土工试验成果及相关文献[13-14]，取土体及挡土墙的材料参数见表1.新旧路基和地基的张拉强度峰值、回弹值均取零，而黏聚力、内摩擦角的峰值、回弹值分别相等.需要特别说明的是，挡土墙材料类型为弹性，其所输入的黏聚力、内摩擦角的峰值仅用于获取强度因子，并不影响应力、位移等分析结果.

表1　土体与挡土墙材料参数

1.3单元剖分与土-墙相互作用模拟

选用高精度6节点三角形单元、均匀分网方式离散土体以及衡重式挡土墙.在土-墙相互作用方面，在挡土墙墙背侧(包括衡重台上方)及底侧设置软件内嵌的接缝单元(Joint element)，其法向、切向刚度分别为100 000 kPa/m和10 000 kPa/m，用以描述接缝单元所受法向应力、切向应力分别与法向位移、切向位移之间的关系；为反映当接缝单元所受切向应力超过抗剪强度时的局部塑性滑动，采用Mohr-Coulomb滑动准则，峰值摩擦角为27°，拉伸强度、峰值黏聚力均为零.因墙背顶部、墙面底部处均为凌空自由面，为更好地描述新路基填土与墙背顶部、地基与墙趾的相对错动，将这两个节点均设置为张开模式，表示接缝分界的端点在有限元网格中代表2个节点，接触面能发生相对滑动，具体如图1局部放大示意.

1.4动态施工力学及墙体外倾变位模拟

因平动模式(T模式)与绕墙趾转动模式(RB模式)均为平动加绕墙趾转动变位模式(RBT模式)的特例，故本文暂以RBT主动外倾变位模式为准，试图研究挡土墙不同主动外倾变位量对路基顶面沉降的影响.首先计算地基和旧路基自重作用产生的初始应力，然后选择“Reset All Displacement”，重置全部位移，即扣除由地基及旧路基自重所产生的位

移量，激活相应单元模拟挡土墙建造及新路基填筑；因是刚性挡土墙，故可在挡土墙墙面相应节点处施加非零位移约束，以模拟挡土墙的主动外倾变位.非零位移约束施加方法如图2所示，即：位置1表示挡土墙原始位置；位置2表示在新路基填筑后，挡土墙在新路基填土作用下发生被动外倾和下沉，此时墙顶A点在水平向、竖直向发生的位移量分别为c和d，墙底B点在水平向、竖直向发生的位移量分别为a和b；位置3表示在位置2基础上，在墙顶A点和墙底B点同时施加不同的非零位移量，以模拟挡土墙的主动外倾变位，其中虚线表示主动外倾变位过程中的平动模式，β角为挡土墙转动外倾的角度，此时墙顶A点水平向位移量为e，竖直向位移量为f，墙底B点水平向位移量为e/2.通过控制墙顶A点的水平向位移量e，即可控制挡土墙平动+绕墙趾转动变位(即RBT模式)主动外倾的数量.

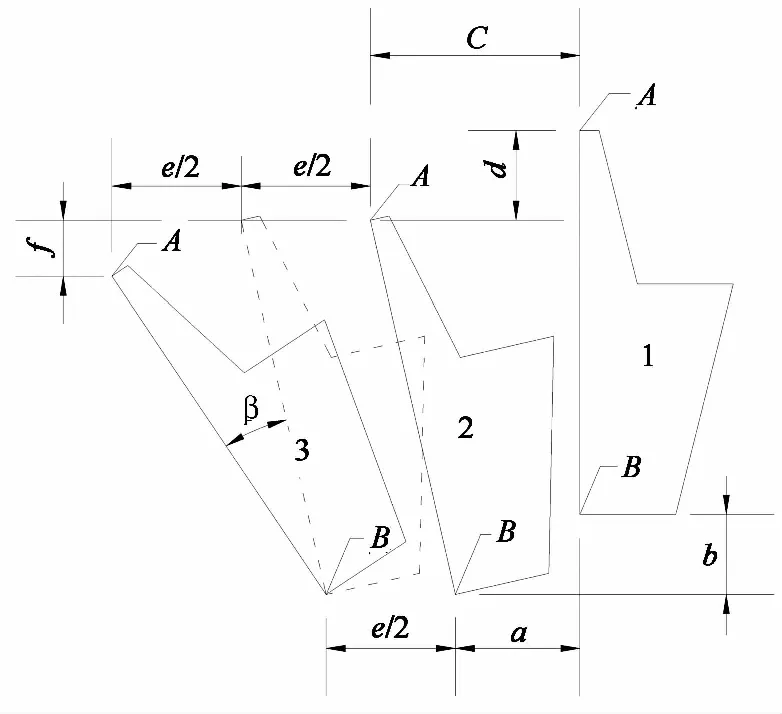
图2　挡土墙外倾变位示意图

2　主要计算结果分析与讨论

2.1挡土墙被动外倾及主动外倾变位后宏观形态对比

图3所示为挡土墙被动外倾及主动外倾变位后新旧路基的总位移云图(单位：m)及外轮廓图(放大因子均取20).可知，总位移相对较大值主要发生于新路基中部，旧路基发生的总位移量较小，挡土墙墙背与新路基发生了相对错动，尤以新路基顶面表现更显著.随着挡土墙RBT主动外倾变位量的增大，新旧路基的总位移数量增加，且影响范围逐渐扩展至旧路基.

2.2新旧路基顶面沉降与挡土墙外倾量的动态变化规律

图3给出了挡土墙被动外倾及RBT模式5种主动外倾变位量下新旧路基顶面沉降值沿路基宽度方向的分布.

(a)挡土墙被动外倾

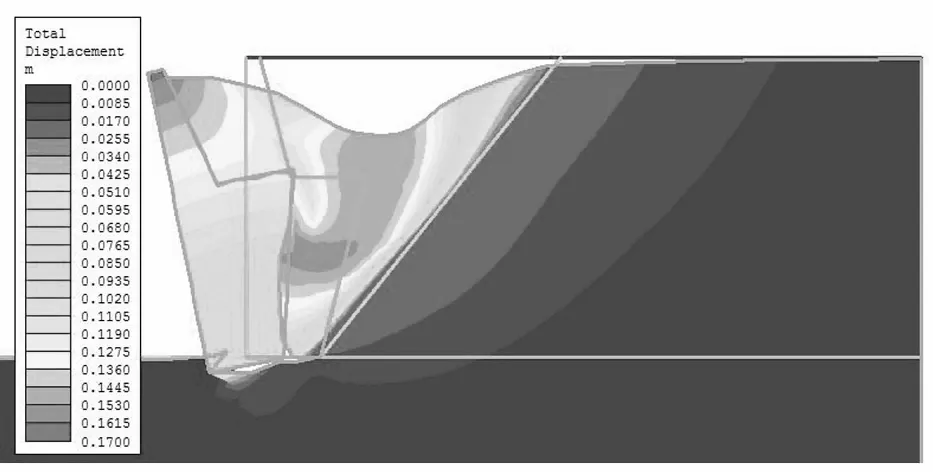
(b)RBT主动外倾(e=0.10 m)

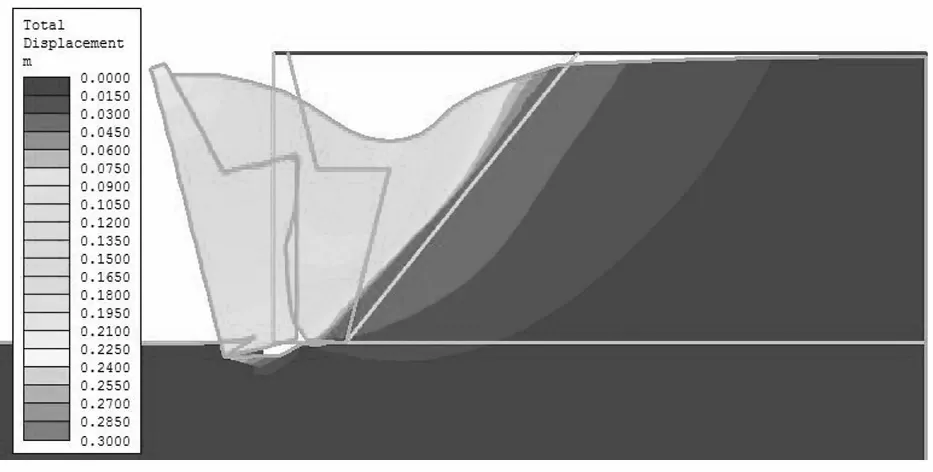
(c)RBT主动外倾(e=0.15 m)

(d)RBT主动外倾(e=0.20 m)

(e)RBT主动外倾(e=0.25 m)

(f)RBT主动外倾(e=0.30 m)

可见，曲线大致分为4段，从左至右依次为翘向右上角直线段、相对平台段、盆状段及近乎直线段.其中新路基与挡土墙墙背衔接面顶部沉降出现突变，这显然与模型中接缝单元端节点设置为张开模式有关，从而使得挡土墙墙背和新路基衔接面顶部能相对自由滑动，形成错台，这也充分说明处理好新路基与挡土墙墙背衔接面的重要性，即新路基与挡土墙结合部位的处置亦不能忽视[11]，在新路基左侧，因挡土墙2.5 m宽的衡重台对其上土体的作用，约1.0 m范围宽的新路基沉降曲线变化平缓，大致呈线性变化，当挡土墙被动外倾时该范围沉降曲线由低变高，而在挡土墙RBT主动外倾变位量增大后，该范围沉降曲线逐渐转变为由高到低.新路基顶面沉降曲线形态大致呈“盆状”分布，当挡土墙主动外倾变位后，新路基顶面曲线形态变得愈加陡峭，沉降盆底变得愈加尖窄，在5种RBT主动变位量下最大沉降均大致出现在新路基的形心对应处，而此位置亦基本是衡重台边缘外侧.随着RBT主动外侧变位量的增大，旧路基顶面沉降值加大，且向新路基方向大致呈线性增加，新旧路基间沉降突变出现于衔接面顶部附近，该处与路基拓宽后路表长大纵向裂缝易发位置吻合.

将文献[2]中工况2的新旧路基顶面沉降曲线一并绘制于图4内，可见，该曲线大致分为3段，从左至右依次为相对平台段、盆状段及近乎直线段，最大沉降值约为38 mm，而本文所获新路基填筑完毕时最大沉降值为64 mm，两者相比，曲线形态及最大值存在一定的差异，可能原因是：1)两者分别采用Phase2和Plaxis软件开展非线性分析，两者土体材料参数、软件所默认的计算精度、收敛准则等存在着差异；2)新路基的填筑方式不同，文献[2]采用水平分层分步填筑，而本模型暂为一次性填筑；3)文献[2]采用Interface单元模拟土-墙相互作用，对墙背顶部节点未作特别处理，意味着这二者节点相互共用，而本模型中节点处理为Joint单元的张开模式，挡土墙与新路基接触面能发生相对滑动，从而可更真实地模拟现实状态.

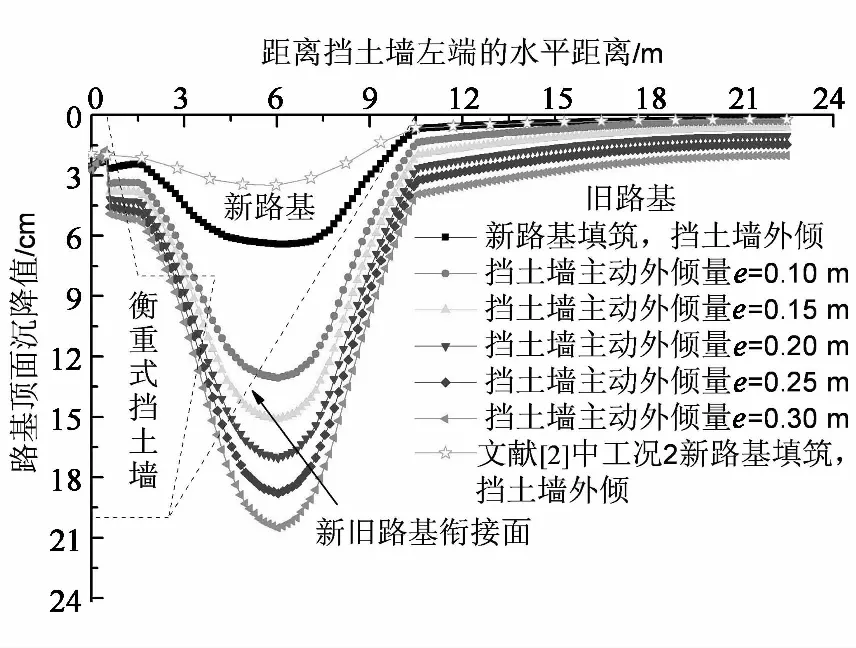
图4　挡土墙外倾量与新旧路基顶面沉降值的动态变化关系

在考虑挡土墙主动外倾变位后，路基顶面最大沉降值陡增，当e=0.10 m时，新老路基顶面最大沉降值为130 mm，最大沉降值比被动外倾时约增加103%.从e=0.10 m增加到e=0.30 m，路基顶面最大沉降值呈非线性增加，当e增加200%时，对应最大沉降值约增加58%，最大沉降值的增长低于主动外倾变化量.

2.3新老路基顶面差异沉降值与挡土墙主动外倾变位量关系

图5给出了挡土墙5种RBT主动外倾变位量下新老路基顶面差异沉降值的变化规律.图中ΔS1,ΔS2,ΔS分别为挡土墙被动外倾产生的初始差异沉降、挡土墙主动外倾产生的附加差异沉降及总差异沉降(ΔS=ΔS1+ΔS2).不难推求，新路基填筑导致挡土墙被动外倾而产生的初始差异沉降在各工况下保持不变，随着挡土墙RBT主动外倾量的增加，因挡土墙主动外倾而产生的差异沉降近线性增加，由二者之和组成的总差异沉降亦呈线性增加.从e=0.10 m到e=0.30 m，挡土墙主动外倾变位量与墙高比值从1%到3%，其值增加200%，总差异沉降值约增加46%，对应附加差异沉降值从66 mm呈非线性增加至123 mm，其值约增加86%.

图6进一步给出了挡土墙RBT模式5种主动外倾变位量下新老路基初始差异沉降与附加差异沉降所占总差异沉降的百分比值.从e=0.10 m到e=0.30 m，挡土墙主动外倾变位量与墙高比值从1%到3%，其值增加200%，新旧路基初始差异沉降值所占比重从49%非线性递减到33%，而附加差异沉降值所占比重从51%非线性递增至67%，由挡土墙主动外倾变位产生的附加差异沉降占总差异沉降的比重约高达50%～70%.

挡土墙主动外倾变位量e/m

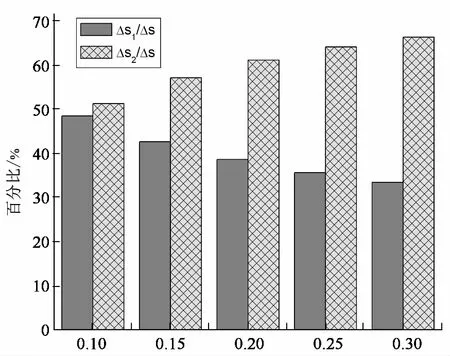
挡土墙主动外倾变位量e/m

3　数值模拟结果的土工离心模型试验验证及比较

文献[10]开展了9组外设衡重式挡土墙的拓宽路基土工离心模型试验，如图7所示.模型率为40，1#～6#为测试新旧路基顶面沉降的电涡流计，采用自制的位移控制装置模拟刚性挡土墙墙体主动外倾，即通过上、下两排螺纹距为1 mm的φ10螺杆的不同旋进量实现挡土墙的不同位移模式及大小，测试墙背土压力、路基顶面沉降、破坏面形态等.选用与本文数值模型前提相近(未考虑土工格栅，衡重式挡土墙以平动+绕墙趾转动形式向外倾斜)的模型3所获试验结果验证本文数值模拟宏观结果的可靠性，其中新路基压实系数为0.88.

图7土工离心模型试验示意(未按比例，单位mm)[12]

Fig.7Geotechnical centrifuge model test

sketch (not to scale,unit: mm)[12]

图8给出了模型试验中挡土墙主动变位下新旧路基顶面总沉降值沿路基宽度方向的分布情况(皆为模型结果).随着挡土墙主动变位量的增加，新旧路基顶面的总沉降值增大，且新路基顶面沉降值较大，旧路基顶面沉降值较小.

表2列出了土工离心模型试验结果，其中ST,SB,ΔS1,ΔS2和ΔS分别为墙顶平移量、墙底平移量、分级加载各阶段对应初始差异沉降值、附加差异沉降值和总差异沉降值，且均为模型结果，未按模型率转换为原型.

挡土墙墙面水平位移/mm

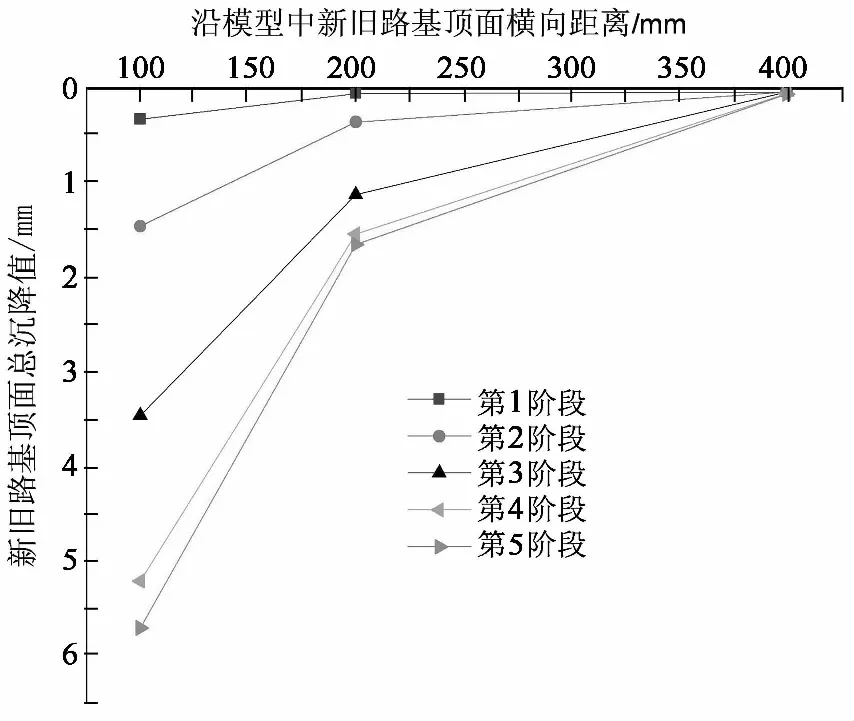
(b) 试验各分级加载阶段新旧路基顶面总沉降值

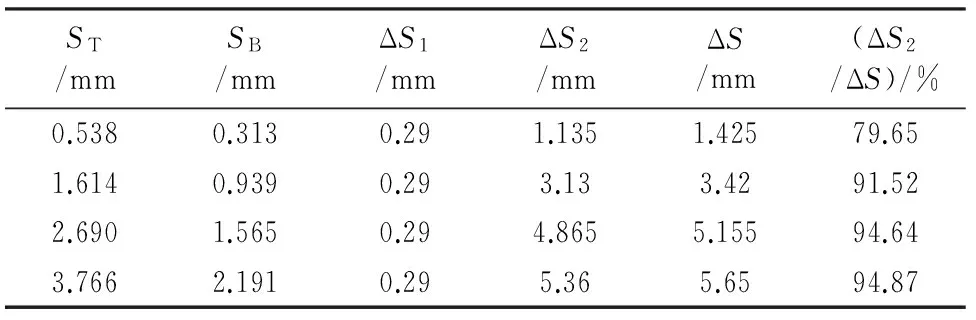
ST/mmSB/mmΔS1/mmΔS2/mmΔS/mm(ΔS2/ΔS)/%0.5380.3130.291.1351.42579.651.6140.9390.293.133.4291.522.6901.5650.294.8655.15594.643.7662.1910.295.365.6594.87

图9进一步给出了附加差异沉降所占权重随挡土墙墙顶外倾变位量与墙高之比而变化的关系.该曲线大致分为翘向右上角陡增、趋于平缓增加2个阶段.当外倾量与墙高之比约为0.18%时，附加差异沉降值所占权重从零陡增至79.65%，说明挡土墙的主动外倾对新旧路基差异沉降有较大影响.当外倾量与墙高之比从0.18%增至1.26%时，附加差异沉降值所占权重从79.65%增至94.87%，增幅相对平缓.

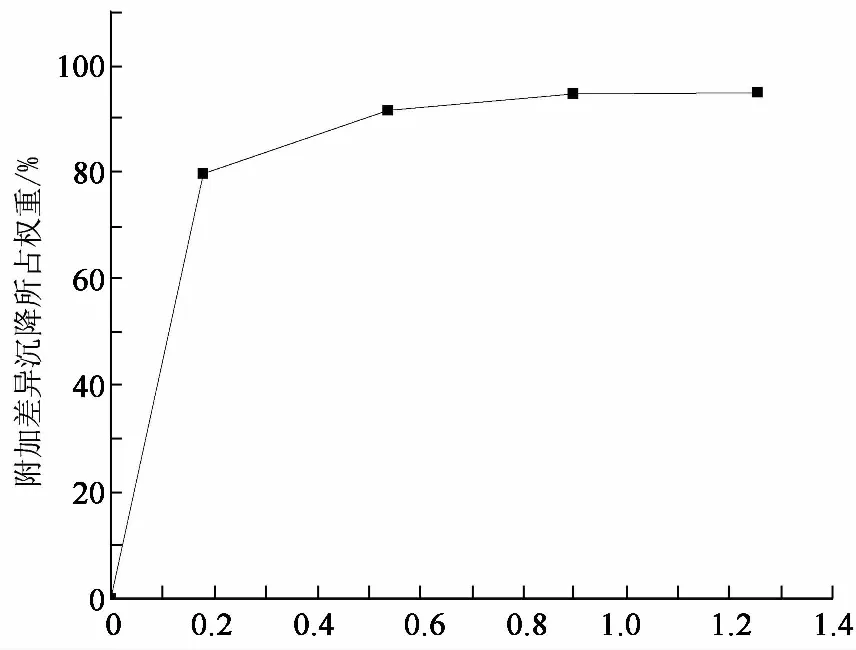
挡土墙墙顶外倾量与墙高之比/%

土工离心模型试验结果表明：当外倾量与墙高之比为1.26%时，模型试验中大约有近9.5成的差异沉降因挡土墙主动外倾而产生，这无疑验证了本文数值模拟宏观结果的正确性，即挡土墙主动外倾变位将对新旧路基差异沉降产生重要影响.当然本文数值模拟得出由当外倾量与墙高之比为1%～3%时，挡土墙产生的附加差异沉降大约占总沉降的51%～67%，两者具体数值上存在差异，可能原因有：1)离心模型试验用压实系数控制压实质量，而数值模拟中采用弹性模量控制压实质量.2)离心模型试验变位历程为分级加载，而数值模拟变位历程为一次加载.3)在离心模型试验中：①未能模拟挡土墙在新路基填土作用下的被动外倾，导致新老路基顶面初始沉降值偏小；②通过自制的位移控制装置模拟刚性挡土墙墙体发生平动、转动或平动+转动等位移模式主动外倾时，需停机实施，然后再重新启动，这势必影响试验结果；③路基表面测点布设过少，依问题的平面应变性，有效测点仅3个，可能未能真实捕捉到路基顶面最大、最小沉降点；④采用刚性底座，未能真实模拟挡土墙基础的潜在下沉等，这些都会对试验结果有较大影响.而在数值模拟中，较好地克服了上述缺陷，较为真实地模拟了挡土墙在新路基填土作用下被动外倾，基础下沉，以及挡土墙与填土之间的相对错动等状态.

4　基于新旧路基差异沉降控制的挡土墙外倾限制阈值确定思路

前文分析表明，挡土墙主动外倾所导致的差异沉降占总差异沉降的比重相对较大，挡土墙主动外倾所导致的差异沉降与挡土墙外倾量(或外倾量与墙高之比)有关，显然，如能控制挡土墙外倾，则挡土墙主动外倾所导致的差异沉降就得以控制，进而总差异沉降得以控制.山区公路拓宽路基挡土墙外倾的限制阈值，可根据新路基-旧路基-挡土墙-路面综合设计的理念，按照如下思路确定：首先由路面材料的抗拉强度和轮载作用下的荷载应力，得到路面结构所能承受的因新旧路基差异沉降产生的最大附加拉应力，然后推求获得总差异沉降值，再由挡土墙主动外倾所导致的差异沉降占总差异沉降的比例关系确定挡土墙外倾的限制阈值.

5　结　论

山区拓宽路基与下设挡土墙相互作用，运用Phase2有限元软件，建立起可真实描述填土-衡重式挡土墙动态相互作用的精细化数值模型，采用两步走、墙面施加非零位移约束方式模拟挡土墙平动+绕墙趾转动变位模式(RBT模式)，分析挡土墙不同主动外倾变位量对新旧路基顶面沉降的影响，并与既有土工离心模型试验结果进行了验证比较，获得如下主要结论：

1)新旧路基顶面沉降曲线形态大致分为4段，即翘向右上角直线段、相对平台段、盆状段及近乎直线段，挡土墙墙背与新路基衔接面顶部及新旧路基衔接面顶部附近出现突变，应加强土-墙结合部、新旧路基结合部等的处置.

2)挡土墙主动外倾变位将导致新旧路基的沉降值增加，新路基顶面沉降曲线形态变得愈加陡峭，且影响范围逐渐扩展至旧路基；最大沉降均大致出现在新路基的形心对应处.

3)数值模型表明，当外倾量与墙高之比为1%～3%时，约51%～67%的差异沉降由挡土墙主动外倾变位产生，这与室内土工离心模型试验宏观结果吻合，但模型试验过高估计了因挡土墙主动外倾变位诱发的附加差异沉降.

4)考虑新老路基差异沉降对路面结构的附加力学影响的时候，应以总差异沉降为准.可根据新路基-旧路基-挡土墙-路面综合设计的理念，参考本文所提出的思路，确定下设刚性土墙外倾的限制阈值，从而尽可能减少山区路基拓宽后路面早期破坏.

参考文献

[1]廖军,陆阳.对支挡约束下拓宽道路不均匀沉降的现场监测系统设计[J].路基工程，2004(4)：57-60.

LIAO Jun，LU Yang.The field monitoring system design to the widening road uneven settlement under the restriction of retaining[J].Subgrade Engineering,2004(4)：57-60.(In Chinese)

[2]同济大学，长沙理工大学.新老路基结合部处治技术研究报告[R].上海：同济大学，2003：115-140.

Tongji University,Changsha University of Science & Technology.New technologies of subgrade widening for highways[R].Shanghai: Tongji University,2003:115-140.(In Chinese)

[3]钱劲松，凌建明.软土地区公路拓宽工程的力学响应分析[J].地下空间与工程学报，2010，6(3)：481-486.

QIAN Jin-song,LING Jian-ming.Analysis of mechanical responses for highway-widening engineering on soft soil foundation[J].Chinese Journal of Underground Space and Engineering,2010,6(3): 481-486.(In Chinese)

[4]张军辉，黄晓明，彭娴.软土地基上高速公路双侧加宽工程的数值分析[J].公路交通科技,2007,24(3): 20-24.

ZHANG Jun-hui,HUANG Xiao-ming,PENG Xian.Numerical analysis of expressway widened with two sides on soft soil foundation[J].Journal of Highway and Transportation Research and Development,2007,24(3):20-24.(In Chinese)

[5]傅珍，王选仓，陈星光，等.拓宽路基差异沉降特性和影响因素[J].交通运输工程学报，2007，7(1)：54-57.

FU Zhen,WANG Xuan-cang,CHEN Xing-guang,et al.Differential settlement characteristics and influencing factors of widening subgrade [J].Journal of Traffic and Transportation Engineering,2007,7(1): 54-57.(In Chinese)

[6]章定文，刘松玉.软土地基高速公路扩建中新老路堤相互作用数值分析[J].中国公路学报，2006，19(6)：7-12.

ZHANG Ding-wen,LIU Song-yu.Numerical analysis of interaction between old and new embankment in widening of freeway on soft ground[J].China Journal of Highway and Transport,2006,19(6): 7-12.(In Chinese)

[7]刘观仕，孔令伟，丁锋，等.高速公路扩建工程软基拓宽的沉降监测与分析[J].岩土力学，2007，28(2)：331-335.

LIU Guan-shi,KONG Ling-wei,DING Feng,et al.Settlement monitoring and analysis for soft foundation of an expressway widening project[J].Rock and Soil Mechanics,2007,28(2):331-335.(In Chinese)

[8]廖敬梅，陆阳，廖军.支挡结构作用下高填路基变形的现场监测[J].路基工程，2005(3)：25-28.

LIAO Jing-mei,LU Yang,LIAO Jun.Field monitoring of the high fill embankment deformation under the restriction of retaining[J].Subgrade Engineering,2005(3)：25-28.(In Chinese)

[9]陆阳，廖敬梅，廖军.高填方路基衡重式挡墙的变形及稳定的现场监测[J].中南公路工程，2006，31(4)：9-13.

LU Yang,LIAO Jing-mei,LIAO Jun.Field monitoring of a gravity balanced retaining wall[J].Central South Highway Engineering,2006,31(4): 9-13.(In Chinese)

[10]张家国.衡重式挡土墙受力及变形特性离心模型实验研究[D].成都：西南交通大学土木工程学院，2004:54-97.

ZHANG Jia-guo.Centrifugal model test study on the soil pressure and deformation of retaining wall with equilibrator[D].Chengdu: School of Civil Engineering,Southwest Jiaotong University,2004:54-97.(In Chinese)

[11]万智，邓宗伟，刘宝琛，等.山区拓宽公路挡土墙路基的受力与变形特征分析[J].岩土力学，2007，28(5)：921-926.

WAN Zhi,DENG Zong-wei,LIU Bao-chen,et al.Loading and deformation characteristics of highway widened subgrade with retaining wall in mountainous region[J].Rock and Soil Mechanics，2007,28(5): 921-926.(In Chinese)

[12]耿建宇.公路路基拓宽改建力学行为及典型工程对策研究[D].成都：西南交通大学土木工程学院，2013：27-38.

GENG Jian-yu.Highway subgrade widening reconstruction mechanical behavior and typical engineering countermeasure research[D].Chengdu: School of Civil Engineering,Southwest Jiaotong University,2013: 27-38.(In Chinese)

[13]钱家欢，殷宗泽.土工原理与计算[M].北京：中国水利水电出版社,1996：44-106.

QIAN Jia-huan,YIN Zong-ze.Principle and calculation of soil engineering[M].Beijing: China Water & Power Press,1996: 44-106.(In Chinese)

[14]JTG D30—2004公路路基设计规范[S].北京：人民交通出版社，2004：58-61.

JTG D30—2004Specifications for design of highway subgrades[S].Beijing: People Communication Press,2004:58-61.(In Chinese)

Mountain Road Widening Embankment Additional Settlement Due to Balance Weight Retaining Wall Extraversion

JIANG Xin1,2,3†,CHEN Tao1,2,3,WU Yu1,2,3,ZHU Qi-jiong4,GENG Jian-yu5,QIU Yan-jun1,2,3

(1.School of Civil Engineering,Southwest Jiaotong Univ,Chengdu,Sichuan610031,China;2.Key Lab of Highway Engineering of Sichuan Province,Southwest Jiaotong Univ,Chengdu,Sichuan610031,China;3.Key Lab of High-speed Railway Engineering of MOE,Southwest Jiaotong Univ,Chengdu,Sichuan610031,China;4.Hangzhou Railway Section,Shanghai Railway Bureau,Hangzhou,Zhejiang310009，China;5.Bridge and Tunnel Engineering Branch,Sichuan Jiaotou Construction Engineering Co,Ltd,Chengdu,Sichuan610041,China)

The retaining structures including the balance weight retaining wall were set up outside the new embankment unilaterally in mountain region highway embankment widening reconstruction.The finite element software phase2was used to build a detailed numerical model for describing the interaction between soil and wall,which introduced the joint element.Based on two-step approach,the nonzero displacement constraints were imposed on metope to simulate translational and rotational (RBT) active extraversion deflection of the retaining wall.The effect of the different deformation amount of active extraversion deflection in the retaining wall on the embankment differential settlement was analyzed.The results were verified and compared with the test results of geotechnical centrifuge model.It shows that the rigid retaining wall is interacted and interdependent well with the new and old embankment.Additional differential settlement,which is caused by the active extraversion deflection of retaining wall,is 51% to 67 % of total differential settlement when the ratio of the extraversion value to wall height is 1% to 3 %.

mountain region highway; embankment widening reconstruction; retaining wall active extraversion deflection; additional differential settlement; FEM

1674-2974(2016)09-0136-08

2015-09-14

国家自然科学基金资助项目(51378440),National Natural Science Foundation of China(51378440); 国家重点基础研究发展计划(973计划)资助项目(2013CB036204); 中央高校基本科研业务费专项资金资助项目(SWJTU12CX067)

蒋鑫(1976-)，男，湖南永州人，西南交通大学副教授，博士

†通讯联系人，E-mail:xjiang01@163.com

U416.1

A