基于无网格有限体积法的弹性地基梁的静态响应分析

张亚萍

（泰州职业技术学院教务处，江苏泰州225300）

基于无网格有限体积法的弹性地基梁的静态响应分析

张亚萍

（泰州职业技术学院教务处，江苏泰州225300）

文章介绍了一种快速、准确、直观的弹性地基梁静态响应分析方法。首先将文克尔地基模型表达的弹性地基梁曲线微分方程改写成含有四个变量的试函数；其次应用无网格有限体积法，采用Matlab语言编写程序，计算弹性地基梁在外载荷作用下的扰度、转角、弯矩和剪力；最后根据用户输入的条件参数，以图形方式输出结果。

文克尔地基模型；无网格有限体积法；交互方式

1　文克尔地基计算模型

弹性地基梁是指搁置在具有一定弹性地基上，各点与地基紧密相贴的梁。如铁路枕木，钢筋混凝土条形基础梁等。通过这种梁，将作用在它上面的载荷，分布到较大面积的地基上，即使承载能力较低的地基，也可以既能承受较大的载荷，又能使梁的变形减小，提高刚度降低内力。弹性地基梁与地基连续接触，梁所受的反力是连续分布的，弹性地基梁具有无穷多个支点和无穷多个未知反力。在弹性地基梁的计算理论中关键问题是如何确定地基的计算模型，现有的地基模型主要有以下6种：文克尔地基模型、利夫金模型、半空间无限体模型、有限压缩层地基模型、邓肯—张模型、弹塑性模型［1］。

由于文克尔地基计算模型相对简单，故在工程实践上被广泛应用。文克尔认为地基每单位面积上所受的压力与地基的变形成正比，地基和基础梁遵循变形协调条件，即梁的扰度和地基的变形是一致的，也就是说即使在出现负的地基反力的时候也不会发生分离。文克尔弹性地基模型中，当基床系数k不变时，弹性地基梁的弹性曲线微分方程为：

式中，E、I分别为梁的弹性模量、截面惯性矩；k为地基系数，y为梁的扰度，q（x）为作用在梁上的载荷，x为梁上计算截面到梁左端的距离。

由材料力学的知识可知，转角θ，弯矩M，剪力q分别为：

梁的支撑方式有：两端固定、两端简支、一端固定另一端自由等等。具体的边界条件为：

当梁为自由端时，y≠0，θ≠0，m=0，q=0（5）

当梁为简支端时，y=0，θ≠0，m=0，q≠0（6）

当梁为固定端时，y=0，θ=0，m≠0，q≠0（7）

2　无网格有限体积法

目前，基于文克尔地基模型的计算方法主要采用初参数法，计算过程比较复杂。首先将文克尔地基模型表达的弹性地基梁曲线微分方程改写成含有四个变量的试函数；其次应用无网格有限体积法，采用Matlab语言编写程序，计算弹性地基梁在外载荷作用下的扰度、转角、弯矩和剪力；最后根据用户输入的条件参数，以图形方式输出结果。

无网格法是利用一组散布在问题域中以及域边界上的节点（而非离散）表示该问题域及其边界。这组散布的节点被称为场节点，它们并不构成网络，即不需要任何事先定义的节点连接信息用于构造未知的场函数。在无网格法中，其问题域通常是由任意分布的场节点表示的，问题域中任意点的场变量是通过该点局部支持域中的一组场节点近似表达的。因此有必要形成基于插值/近似技术的移动域来构造无网格形函数，用于表示适应任意分布节点的场函数近似。目前已提出了数种构造无网格形函数的方法［2-3］，如最小移动二乘法，紧支径向基函数法，Shepherd函数法等等。文中的无网格有限体积法选择最小移动二乘法构造形函数。

2.1最小移动二乘法（MLS）

移动最小二乘法（MLS），利用区域上的n个离散点构造一个连续光滑曲面来逼近真实场函数。

考虑域Ω中一场变量的未知标量函数u（x），定义在x处的u（x）的MLS近似表达式为：

其中，pT（x）=［1，x，x2，Lxn］，a（x）为一系数向量，该系数a可以通过下列加权离散L2范数取最小而得到：

其中dI=|| x-xI，代表xI到x的距离，rI为节点xI的支持域半径。

J关于a（x）求驻点值可得到

该运算将产生如下线性关系

从而可以到：

其中：A（x）=PTW（x）P

由Aα′=p′-A′α，可得到MLS形函数Φ的一阶导数：

2.2无网格有限体积法的公式

弹性扰曲方程（1）可写为：

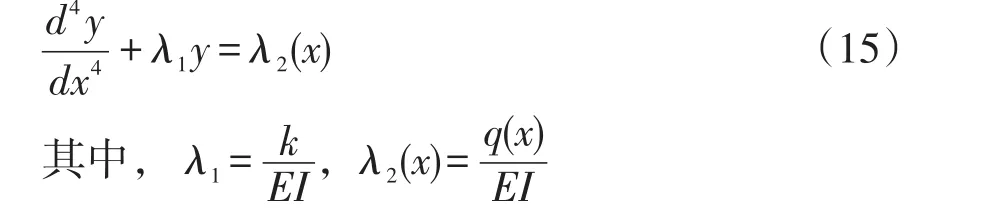
将位移，转角，动量和剪力作为独立变量考虑，则4阶常微分方程（15）可写为四个一阶常微分方程：

用矩阵向量的形式表示为：

设权函数为W，则（20）式的加权残量弱形式为：

用移动最小二乘函数（MLS）分别构建u，θ，m，q四个变量的试函数：

用矩阵向量的形式表示为：

这样在每个xI节点存在四个变量uI，θI，mI，qI，在每个节点配点，则由公式（20）（26）得到以下的配点公式：

假设节点xI的局部区域为ΩI=｛x|xI-lI＜x＜xI+lI，x∈Ω｝，子区域ΩI上的Heaviside函数可定义为：

Heaviside函数作为权函数，则公式（27）可写为：

则边界条件可写为：

3　数值算例

设弹性地基梁的弯曲刚度为EI（bending rigidity），地基系数为k（Foundation modulus），外部载荷为p（x）（Force），支撑方式（SupportMode= ssccsccs）分为四种：两端简支（ss）、两端固支（cc）、左端简支右端固支（sc）、左端固支右端简支（cs），弹性地基梁的长度为L（Length of Beam）。

算例1：设弹性地基梁的弯曲刚度EI= 40000KNm2，地基系数为k=106KN/m2，承受均布载荷p=10KN/m，两端简支，弹性地基梁长度为L= 1m。参数输入如图1所示，程序计算的弹性地基梁的扰度、转角、弯矩、剪力如图2所示。

图1　参数输入

图2　计算结果输出 （a）扰度、（b）转角、（c）弯矩、（d）剪力

算例2：设弹性地基梁的弯曲刚度EI= 20000KNm2，地基系数为k=5×105KN/m2，承受抛物线载荷p=x2KN/m，两端固支，弹性地基梁长度为L=1m。参数输入如图3所示，程序计算的弹性地基梁的扰度、转角、弯矩、剪力如图4所示。

4　总结

将四阶弹性扰曲微分方程用四个未知参数表示，不仅提高了计算的精度，而且也降低了对最小移动二乘法形函数的连续性要求。程序采用参数化设计，交互式输入，图形化显示，为分析基于文克尔地基模型弹性地基梁的静态响应提供了一种快速、准确、直观的计算方法。

图3　参数输入

图4　计算结果输出（a）扰度、（b）转角、（c）弯矩、（d）剪力

［1］高屹.浅谈弹性地基梁设计模型与计算方法［J］.甘肃科技，2003（3）：54-55.

［2］S.N.Atluri，S.shen.The meshless local Petrov-Galerkin（MLPG）method［M］.Ecino：Tech Science Press，2002.

［3］S.N.Atluri.The meshless method（MLPG）for domain &BIE discretizations［M］.Ecino：Tech Science Press，2014.

（责任编辑刘红）

The Static Response Analysis of Beam on Elastic Foundation Based on Meshless Finite Volume Method

ZHANG Ya-ping
（Taizhou Polytechnic College，Taizhou Jiangsu 225300，China）

The article provides a simple，efficient and intuitive way to investigate the static response of a beam on winkler foundation.Firstly，the article rewrites the differential equation for the deflection curve of a beam on elastic foundation，based on winkler model，as a system of four one order differential equations.Secondly，the finite volume method is applied to calculate the degree of deflection，rotation，bending moment and shearing force of elastic foundation beam under external load by using Matlab language.Finally，the interactive mode is used to input the parameters，and the results of the analysis are graphically output.

winkler foundation model；meshless finite volume method；interactive mode

TU470+.3，TU471+.2

A

1671-0142（2016）04-0053-04

张亚萍（1978-），女，江苏泰兴人，副教授.