Copula熵方法及其在三变量洪水频率计算中的应用

李　帆,郑　骞,张　磊

(1. 扬州大学水利与能源动力工程学院,江苏 扬州　225000;2. 衢州市水利局,浙江 衢州　324000; 3. 徐州市水利建筑设计研究院,江苏 徐州　221116)



Copula熵方法及其在三变量洪水频率计算中的应用

李帆1,郑骞2,张磊3

(1. 扬州大学水利与能源动力工程学院,江苏 扬州225000;2. 衢州市水利局,浙江 衢州324000; 3. 徐州市水利建筑设计研究院,江苏 徐州221116)

为解决传统Copula方法在进行联合概率分布拟合过程中要先进行函数类型选择的问题,将Copula函数和最大熵原理进行耦合,通过求解具有最大熵的Copula方程,求得二维联合分布函数,即Copula熵方法。用求得的Copula函数对洪水事件的3个相关变量(洪峰流量、洪水总量和洪水历时)进行两两配对的二维联合分布拟合,并利用Gibbs采样方法和Copula函数实现三变量洪水事件的随机模拟。以淮河鲁台子水文站的实测洪水资料为研究对象,进行实例分析,并通过拟合优度的计算,证明Copula熵方法对多维相关变量概率拟合的有效性以及Gibbs采样方法在三变量洪水事件模拟过程中的有效性。

洪水频率;联合分布函数;Copula函数;最大熵原理;Copula熵方法;淮河;鲁台子水文站

洪水事件的概率估计是防洪规划、水利工程建设和水资源管理的重要依据。一个洪水事件一般可以由3个具有相关关系的随机变量来描述,即洪峰流量(P)、洪水总量(V)和洪水历时(D)。Copula函数方法是一种实现多变量洪水事件联合分布拟合的有效途径,并在水文领域中被广泛应用。郭生练等[1]对Copula函数在水文中的应用进行了综述;宋松柏等[2]系统地探讨了各种Copula函数结构在西北典型流域中的应用,分析了Copula函数在多变量水文计算领域的适用性及优越性。Copula函数存在多种形式,其中二维Archimedean Copula函数应用最广泛。常用的Archimedean Copula函数包括Frank Copula、Gumbel Copula和Clayton Copula等类型,此外还有属于椭圆Copula函数的Gaussian Copula等。针对具体问题选取合适的Copula函数进行多维联合概率分布拟合。Salvadori等[3]用Archimedean Copula函数建立了最高洪水位与洪水总量、洪峰流量与洪水总量、降水强度与降水历时的3组二维联合分布,分析了Gumbel Copula和Frank Copula函数在水文二维极值联合分布构建上的有效性。Zhang 等[4]用4种Archimedean Copula 函数构造了洪峰与洪水总量、洪水总量与洪水历时的2组二维联合分布,并比较了他们的拟合优度,认为Gumbel Copula对所选河流洪水的拟合最好。肖义等[5]、李天元等[6]用Gumbel Copula函数构造边缘分布为P-Ⅲ型分布的两变量联合分布,用以描述洪峰和洪水总量。Renard等[7]探讨了Gaussian Copula在洪水频率分析上的应用。李计等[8]比较了4种对称的Archimedean Copula和5种非对称的Archimedean Copula对干旱历时、干旱烈度和烈度峰值3个干旱特征变量联合分布的拟合效果。虽然Copula函数的应用已十分广泛,但在进行Copula函数参数的估算之前,必须先要对Copula函数的类型进行选择,然后再进行拟合分析。这种选型过程往往并不完全客观,从而造成计算结果不准确。为了避免这种由于选型而造成的偏差,本文将最大熵原理和Copula函数理论进行耦合,即Copula熵方法,用以求得联合概率分布密度函数。另外,传统的Copula方程都是两变量的联合分布方程,在向三维变量拓展时往往比较困难,计算也比较复杂。笔者基于蒙特卡洛算法,利用Gibbs采样方法和Copula函数,生成大量洪水事件,从而实现对三变量的洪水事件的随机模拟,进而分析洪水事件的发生概率，并以淮河鲁台子水文站实测资料为对象,进行了示例研究。

1　理论与方法

1.1Copula函数

由Sklar定理可得二维Copula函数:

(1)

式中:F(x1,x2)——联合概率分布函数;F1(x1)=u、F2(x2)=v——边缘分布函数。

根据Sklar定理,若边缘分布函数是连续的,则Copula函数C(u,v)唯一。

1.2最大熵原理与Copula熵

根据熵理论,对于一个连续的随机变量X∈[a1,a2],若概率密度函数为f(x),则其熵可定义为

(2)

根据最大熵原理(POME),当H取得最大值时,人为假定最小,从而可以得到最合乎自然、最为超然、偏差最小的f(x)[9]。对于Copula函数,其对应的Copula熵为

(3)

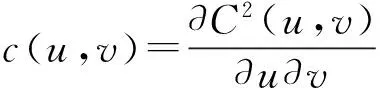
式中:c(u,v)——二维Copula概率密度函数。

根据POME,式(3)中使得W最大的c(u,v)即为最适合的联合概率密度函数。

1.3求解Copula概率密度函数

为计算最优的c(u,v),可以利用拉格朗日乘子法对式(3)进行求解。根据Copula概率密度函数的性质,可列出以下约束条件:

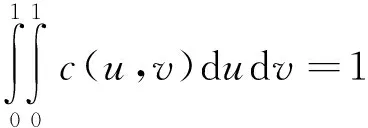
(4)

(5)

(6)

式中:r——r阶矩;ρ——Spearman秩相关系数。

Chu[10]证明,使得式(3)取得最大值的c(u,v)的表达式为

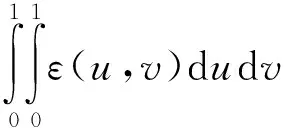
(7)

其中

式中:α、β、λ——待求系数;n——矩的阶数。

式(7)没有解析解,可以使用牛顿迭代法计算待求系数[11],进而求得Copula概率密度函数的表达式。

1.4Gibbs采样方法生成三变量洪水事件

Copula熵方法在理论上可以直接从二维扩展到三维,得到三变量Copula概率密度函数,但计算量较大,比较耗时。笔者采用Gibbs采样方法[12]和二维Copula函数进行三维随机变量模拟,这种方法原理简单,计算速度快,并已在海浪波况的随机模拟中成功运用[13-14]。

令X、Y、Z为洪峰流量、洪水总量和洪水历时的随机变量,x、y、z分别表示洪峰流量、洪水总量、洪水历时的累计频率,cXY和cXZ分别表示洪峰流量与洪水总量的Copula密度函数和洪峰流量与洪水历时的Copula密度函数。随机生成4个0～1之间的随机数(a,b,c,d),令y0=a,并使得

(8)

由式(8)可求得x1,把x1代入

(9)

(10)

可分别求得y1和z1。重复以上步骤可以得到任意多组三维模拟值(x,y,z),然后利用边缘概率分布函数的反函数将(x,y,z)转换成其所对应的物理值,得到任意多个三变量洪水事件,从而利用模拟的洪水事件进行概率的估计和分析。

2　结果与分析

以淮河干流鲁台子水文站多年(1954—1998年)洪水观测资料为研究对象,验证Copula熵方法的有效性。鲁台子水文站位于淮河中游,控制面积88 630 km2,多年平均流量693 m3/s,资料长度45 a。为了充分利用观测数据,采用超阈值法选取洪水事件。流量超过2 000 m3/s的时刻,定义为洪水事件的起始时间,流量低于2 000 m3/s的时刻,定义为洪水事件的结束时间。为了保证洪水事件的独立性,规定2个洪水事件之间的间隔不小于3 d,否则,两场洪水将合并为一场洪水。根据该定义方法,共从原始观测资料中提取出56场洪水事件。

表1　各分布函数的拟合优度Table 1　Goodness-of-fit for different distribution functions

2.1边缘分布拟合

分别用P-Ⅲ分布、广义帕累托分布(Generalized Pareto Distribution,GPD)、广义极值分布(Generalized Extreme Value distribution,GEV)、Gamma分布和指数分布对观测值进行拟合,并通过计算归一化均方差(Normalized Mean Square Error,NMSE)与经验分布进行比较。结果表明P-Ⅲ分布的拟合效果最好(表1)。图1为P-Ⅲ理论分布曲线与经验点据的拟合情况。

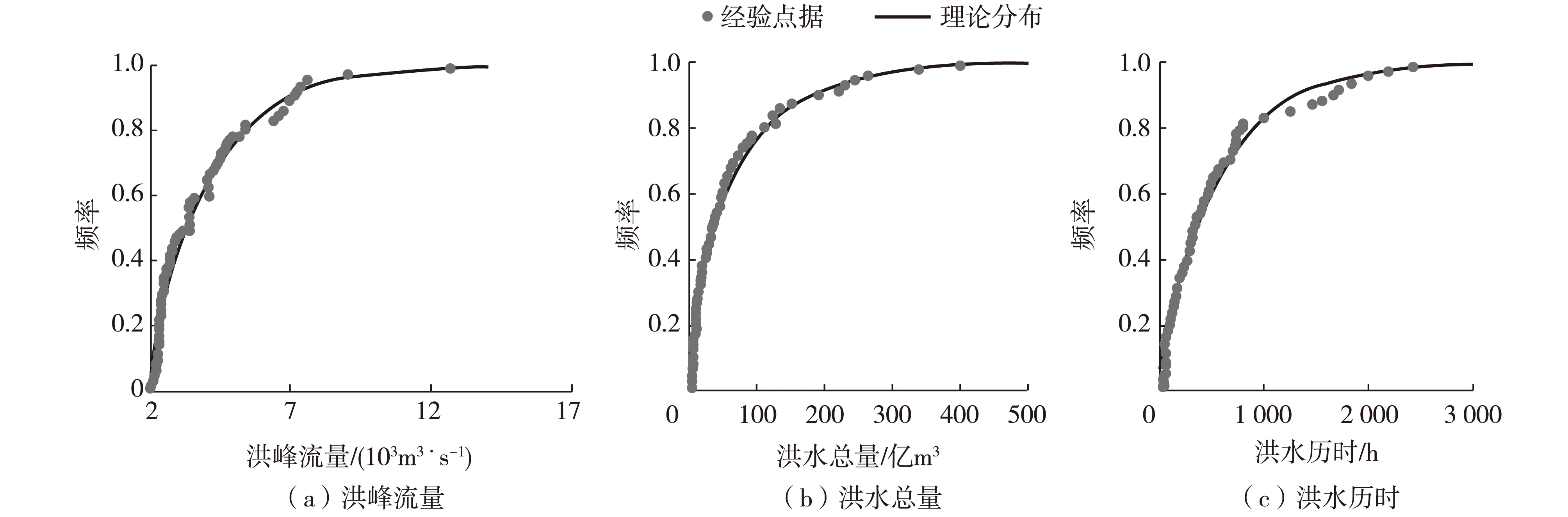
图1　洪水事件三要素的理论分布曲线与经验点据Fig. 1　Theoretical distribution curves and empirical cumulative distribution functions of flood variables

2.2Copula密度函数计算

按照1.3中方法进行系数估计,当式(7)中的n分别取2和3时,计算得到的各系数见表2。当n=3时,系数α3和β3非常小,表明ε(u,v)只需展开到n=2即可。于是可得到3个二元Copula密度函数:

(11)

则Copula累积概率分布函数可表示为

(12)

表2　两变量Copula函数系数Table 2　Parameters of bivariate copula functions

利用得到的累计概率分布函数及联合重现期公式得到图2中的联合重现期等值线(重现期单位为a)。联合重现期表示其中一个变量超过某一定值的概率,其公式见文献[3],本文平均每年发生的洪水次数取为56/45。

2.3三变量洪水事件模拟

由于使用了超阈值方法进行洪水事件的选取,所以每年发生洪水事件的次数也需要进行估计。笔者使用经验频率来估计每一年洪水的发生次数。在45 a(1954—1998)间,没有发生超阈值洪水的年数是10,发生1次的有14 a,发生2次的有17 a,发生3次的有6 a,即P(n=0)=10/45,P(n=1)=17/45,P(n=2)=12/45,P(n=3)=6/45。结合1.3节中的Gibbs采样方法,得到1 000 a的模拟洪水事件(图2)。

图2　1 000 a的洪水模拟事件与观测值以及两变量联合重现期等值线Fig. 2　Observations and simulated flood events with a 1000-year return period and bivariate joint return period contours

2.4洪水事件的拟合优度评估

为定量估计Copula熵方法与Gibbs采样方法的有效性,分别计算观测值与模拟值的经验频率,并进行比较。其中,三变量经验频率定义为[15-16]

(13)

式中:K——满足的样本个数,m——总的样本个数。

表3　卡方检验与K-S检验结果Table 3　Results of Chi squared test and K-S test

两变量经验频率的定义与式(13)相似。利用卡方检验与K-S(Kolmogorov-Sminov)检验来进行模拟值与实测值的比较。表3给出了2种检验方法的计算结果,如果卡方统计值小于临界值,K-S检验的P值大于0.05,则表明在5%的显著水平下通过假设检验,说明拟合情况较好,反之则不通过假设检验,说明拟合情况无法达到要求。计算结果表明,模拟值在5%的显著性水平下与样本的拟合较好,能够反映实测洪水的统计特征。

3　结论与展望

a. Copula熵方法与Copula方法类似,可以通过任意边缘分布和变量间的相关性构建二维的联合概率分布函数,与单纯的Copula方法比较,Copula熵方法省去了Copula方程类型选择这一过程,计算效率更高。

b. 结合Gibbs采样方法和二维Copula函数,可以利用二维联合概率分布函数和条件概率函数进行三维随机变量的模拟,从而实现对三变量洪水事件的概率模拟。以淮河干流鲁台子水文站为研究对象,应用上述方法结合1954—1998年间的洪水实测资料,对洪水事件进行了概率模拟,模拟结果和检验结果显示,利用Copula熵方法对二维联合分布进行拟合适用且有效。此外,Gibbs采样方法可以实现对三变量洪水事件的随机模拟,模拟结果通过了拟合优度检验。该方法可以为该地区的水利工程规划、洪水风险评估以及水资源合理利用提供参考依据。

c. Copula熵方法在水文领域中的应用还处于起步阶段,相关的研究还比较少,有必要对该方法进行更为深入的研究。本文仅对Copula熵方法进行了简单的介绍,并用一个实例进行了验证。Copula熵方法在其他地区及领域的有效性以及与传统Copula函数拟合效果的比较还需要进一步研究与分析。此外,Copula在求解联合分布方程的过程中,不同约束条件对拟合结果的影响等问题也需要进一步讨论。

[1] 郭生练,闫宝伟,肖义,等. Copula 函数在多变量水文分析计算中的应用及研究进展[J]. 水文, 2008,28(3): 1-7. (GUO Shenglian, YAN Baowei, XIAO Yi, et al. Multivariate hydrological analysis and estimation[J]. Journal of China Hydrology, 2008, 28(3): 1-7. (in Chinese))

[2] 宋松柏, 蔡焕杰, 金菊良,等. Copulas函数及其在水文中的应用[M]. 北京: 科学出版社, 2012.

[3] SALVADORI G, DE MICHELE C. Frequency analysis via Copulas: theoretical aspects and applications to hydrological events [J]. Water Resources Research, 2004, 40(12):1-17.

[4] ZHANG L, SINGH V P. Bivariate flood frequency analysis using the Copula method [J]. Journal of Hydrologic Engineering, 2006, 11(2): 150-164.

[5] 肖义, 郭生练, 熊立华, 等. 一种新的洪水过程随机模拟方法研究[J]. 四川大学学报(工程科学版), 2007, 39(2): 55-60. (XIAO Yi, GUO Shenglian, XIONG Lihua, et al. A new random simulation method for constructing synthetic flood hydrographs[J]. Journal of Sichuan University(Engineering Science Edition), 2007, 39(2): 55-60. (in Chinese))

[6] 李天元, 郭生练, 刘章君, 等. 基于峰量联合分布推求设计洪水[J]. 水利学报, 2014, 45(3):269-276. (LI Tianyuan, GUO Shenglian, LIU Zhangjun et al. Design flood estimation based on bivariate joint distribution of flood peak and volume [J]. Journal of Hydraulic Engineering, 2014, 45(3): 269-276. (in Chinese))

[7] RENARD B, LANG M. Use of a Gaussian Copula for multivariate extreme value analysis: some case studies in hydrology [J]. Advances in Water Resources, 2007,30: 897-912.

[8] 李计,李毅,宋松柏,等. 基于Copulas 函数的多维干旱变量联合分布[J]. 自然资源学报, 2013,28(2): 312-320. (LI Ji, LI Yi, SONG Songbai, et al. Multivariate joint distributions of drought variables based on Copulas function[J].Journal of Natural Resources, 2013, 28(2): 312-320. (in Chinese))

[9] 王栋,朱元甡. 最大熵原理在水文水资源科学中的应用[J]. 水科学进展,2001,12(3):424-430. (WANG Dong, ZHU Yuansheng. Principle of maximum entropy and its application in hydrology and water resources[J]. Advances in Water Science, 2001, 12(3): 424-430. (in Chinese))

[10] CHU B. Recovering Copulas from limited information and an application to asset allocation[J]. Journal of Banking and Finance, 2011, 35: 1824-42.

[11] AGHAKOUCHAK A. Entropy-Copula in hydrology and climatology [J]. Journal of Hydrometeorology, 2014,15: 1-13.

[12] GEMAN S, GEMAN D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1984,20: 25-62.

[13] LI F, VAN GELDER P H A J M, RANASINGHE R, CALLAGHAN D P, JONGEJAN R B. Probabilistic modelling of extreme storms along the Dutch coast[J]. Coastal Engineering, 2014,86(4): 1-13.

[14] CALLAGHAN D P, NIELSEN P, SHORT A, et al. Statistical simulation of wave climate and extreme beach erosion[J]. Coastal Engineering, 2008, 55(5): 375-390.

[15] SALVADORI G, DE MICHELE C. Frequency analysis via Copulas: theoretical aspects and applications to hydrological events[J]. Water Resources Research, 2004, 40: 1-17.

[16] ZHANG L, SINGH V P. Trivariate flood frequency analysis using the Gumbel-Hougaard Copula[J]. Journal of Hydrological Engineering, 2007,12: 431-439.

Copula entropy method and its application to trivariate flood frequency calculation

LI Fan1, ZHENG Qian2, ZHANG Lei3

(1.SchoolofHydraulic,Energy,andPowerEngineering,YangzhouUniversity,Yangzhou225000,China;2.QuzhouWaterConservancyBureau,Quzhou324000,China;3.XuzhouHydraulicConstructionandDesignResearchInstitute,Xuzhou221116,China)

In order to avoid selection of the type of functions when using traditional copula methods to fit the joint probability distribution, the copula function and the maximum entropy principle were jointly used (in a method also called the copula entropy method), and the two-dimensional joint distribution functions of flood variates were obtained by solving the copula function with the maximum entropy. With the solved copula function, the two-dimensional joint distribution functions of flood variates (peak discharge, flood volume, and flood duration) were mutually constructed. The Gibbs sampling method and copula functions were used to stochastically simulate trivariate flood events. A case study was conducted using the observed flood data from the Lutaizi Hydrological Station on the Huaihe River. A goodness-of-fit analysis shows that the copula entropy method is effective in fitting multivariate probability distributions and the Gibbs sampling method is effective in simulating trivariate flood events.

flood frequency; joint distribution function; copula function; maximum entropy principle; copula entropy method; Huaihe River; Lutaizi Hydrological Station

10.3876/j.issn.1000-1980.2016.05.011

2015-12-07

江苏省高校自然科学研究项目(15KJD170003);扬州大学科技创新培育基金(2015CXJ027)

李帆(1982—),男,辽宁营口人,讲师,博士,主要从事水文统计研究。E-mail:lifan@yzu.edu.cn

P333.2

A

1000-1980(2016)05-0443-06