满模拟下的一些保持性*

李 娜

满模拟下的一些保持性*

李 娜

令F和F'是两个模态框架,本文(不用对应理论)首先证明当f是F到F'上的满同态时,f具有一些保持性;第二,证明了如果Z是框架F到F'上的一个满模拟,那么Z具有一些保持性质。第三,证明了模拟的等价条件和互模拟的等价条件以及满模拟和互模拟关系;第四,定义了生成子框架并证明了:如果F'是F的生成子框架,那么F'也具有一些保持性质;第五,定义了F和F'的不交并FF'并证明了它也具有一些保持性质。最后,证明了任意的非空模型M与一个禁自返模型之间存在一个满模拟。关键词:满同态;满模拟;互模拟;不交并

一、引言

数学家和逻辑学家都很少孤立地考察两个集合A和A′之间的关系。而是考察带有运算°和°′的两个集合〈A,°〉和〈A′,°′〉，这样的集合通常称为结构。他们不仅对不同结构之间的关系感兴趣，而且还对结构本身所具有的各种不同的性质感兴趣。他们研究哪些结构的性质在这样的关系或运算下保持？例如，如果两个代数结构〈A,°〉与〈A′,°′〉是同态的，那么当°满足结合律时，°′也满足结合律，并称同态保持运算的结合性。本文在模态逻辑的框架中讨论，对于两个框架(结构)F=〈W,R〉和F′=〈W′,R′〉，在什么样的条件下，当R具有某种性质φ时，R′也具有。特别地，给出比同态弱的概念——满模拟关系，证明：当R具有某些性质φ时，R′也具有。即框架的自返性、对称性、传递性、等价性、确定性、持续性、欧性、孤立性、稠密性等等在满模拟下保持。

二、基本概念

定义1 设F=〈W,R〉是任意的一个二元组，F=〈W,R〉是一个框架，当且仅当，W是任意的一个非空集合，R是W上的任意的一个二元关系，即R⊆W×W。

定义2 令F=〈W，R〉是一个任意的框架，

(1)称框架〈W,R〉是自返-框架，如果对于任意的w∈W，都有wRw。

(2)称框架〈W,R〉是对称-框架，如果对于任意的w,w′∈W，wRw′⟹w′Rw。

(3)称框架〈W,R〉是传递-框架，如果对于任意的w,w′,w″∈W，wRw′并且w′Rw″⟹w′Rw″。

(4)称框架〈W,R〉是等价-框架，如果R是自返的、对称的和传递的。

(5)称框架〈W,R〉是确定-框架，如果对于任意的w,w′,w″∈W，wRw′并且wRw″⟹w′=w″。

(6)称框架〈W,R〉是持续-框架，如果对于任意的w∈W，存在u∈W使得wRu。

(7)称框架〈W,R〉是欧性-框架，如果对于任意的u,v,w∈W，

uRv并且uRw⟹vRw或者wRv。

(8)称框架〈W,R〉是孤立-框架，如果对于任意的x,a∈W，aRx⟹x=a。

(9)称框架〈W,R〉是稠密-框架,如果对于任意的a,b∈W,aRb,存在一个x∈W使得

aRx并且xRb。

(10)称框架〈W,R〉是树状-框架，如果对于任意a,b,c∈W使得

bRa并且cRa⟹bRc或者cRb。

(11)框架〈W,R〉的一个关系′是良基的,如果不存在如下的元素序列(ar|γ<ω)：

a0→a1→…→aγ→…(γ<ω)。

三、一些基本的保持性

定义3 令F=〈W,R〉和F′=〈W′,R′〉是两个框架。f是一个从W到W′的映射并且具有性质：如果wRu那么f(w)R′f(u)(同态条件)，则称f是框架F到框架F′的一个同态映射，记作 f：〈W,R〉→〈W′,R′〉。

定义4 令F=〈W,R〉和F′=〈W′,R′〉是两个框架。f是一个从W到W′的满射并且具有性质：对任意的w,u∈W，如果wRu，那么f(w)R′f(u)(同态条件)。则称f是框架F到框架F′的一个满同态并称框架F和框架F′同态，记作 F～F′。如果存在一个从F到F′的一个双射的同态，则称F同构于F′，记作F≅F′。

在定义4中，f(R)={f(w)R′f(u)|wRu,对任意的w,u∈W}。

定理5 令F=〈W,R〉和F′=〈W′,R′〉是两个框架。若F～F′，则下面的结论(1)—(11)成立：

(1) 如果关系R在F中是自返的，那么关系R′在F′中也是自返的。

(2) 如果关系R在F中是对称的，那么关系R′在F′中也是对称的。

(3) 如果关系R在F中是传递的，那么关系R′在F′中也是传递的。

(4) 如果关系R在F中是等价的，那么关系R′在F′中也是等价的。

(5) 如果关系R在F中是确定的，那么关系R′在F′中也是确定的。

(6) 如果关系R在F中是持续的，那么关系R′在F′中也是持续的。

(7) 如果关系R在F中是欧性的，那么关系R′在F中也是欧性的。

(8) 如果关系R在F中是孤立的，那么关系R′在F′中也是孤立的。

(9) 如果关系R在F中是稠密的，那么关系R′在F′中也是稠密的。

(10)如果关系R在F中是树状的，那么关系R′在F′中也是树状的。

(11)如果转换关系→在F中是传递的、良基的，那么转换关系→′在F′中也是传递的、良基的。

证明因为F～F′，所以，不妨设f是一个从W到W′的满射并且满足同态条件。

(1)对于任意的w′∈W′，因为f是一个从W到W′的满射，所以存在w∈W使得f(w)=w′。因为关系R在F中是自返的，即：wRw，再由f的同态性可得：f(w)R′f(w)。即：w′Rw′，故：关系R′在F′中也是自返的。

(2)对于任意的u′,v′∈W′，假设u′R′v′成立，因为f是一个从W到W′的满射，所以存在u,v∈W使得f(u)=u′并且f(v)=v′。由R′=f(R)可得：uRv。再由R的对称性可得：vRu。再由R′=f(R)可得：f(v)R′f(u)。即：v′R′u′，故：关系R′在F′中是对称的。

(3) 对于任意的u′,v′,w′∈W′，假设u′R′v′并且v′R′w′成立，因为f是一个从W到W′的满射，所以存在u,v,w∈W使得f(u)=u′并且f(v)=v′并且f(w)=w′。又因R′=f(R)，所以，uRv并且vRw成立。由R在F中是传递的可得：uRw。再由R′=f(R)可得：f(u)R′f(w)，即：u′R′w′。故：关系R′在F′中是传递的。

(4)由(1)-(3)可得。

(5)对于任意的u′,v′,w′∈W′，假设u′R′v′并且u′R′w′成立，因为f是一个从W到W′的满射，所以存在u,v,w∈W使得f(u)=u′并且f(v)=v′并且f(w)=w′。又因R′=f(R)，所以，uRv并且uRw成立。由R在F中是确定的可得：v=w。再由f是一个从W到W′的映射可得：f(v)=f(w)，即：v′=w′。故：关系R′在F′中是确定的。

(6)对于任意的u′∈W′，因为f是一个从W到W′的满射，所以存在u∈W使得f(u)=u′。因为R是持续的，所以存在v∈W使得uRv成立。又因f是一个从W到W′的映射，所以f(v)∈W′。在利用uRv可得：f(u)R′f(v)。故：关系R′在F′中是持续的。

(7)对于任意的u′,v′,w′∈W′，假设u′R′v′并且u′R′w′成立，因为f是一个从W到W′的满射，所以存在u,v,w∈W使得f(u)=u′并且f(v)=v′并且f(w)=w′。又因R′=f(R)，所以，uRv并且uRw成立。由R是欧性的得：vRw或者wRv。由f是一个从W到W′的映射并且R′=f(R)可得：f(v)R′f(w)或者f(w)R′f(v)成立，即：v′R′w′或者w′R′v′。故：关系R′在F′中是欧性的。

(8)对于任意的a′,x′∈W′，假设a′R′x′成立，因为f是一个从W到W′的满射，所以存在a,x∈W使得f(a)=a′并且f(x)=x′。又因R′=f(R)，所以，aRx。由R在F中是孤立的可得：x=a。由f是一个从W到W′的映射可得：f(x)=f(a)，即：x′=a′。故：关系R′在F′中是孤立的。

(9)对于任意的a′,b′∈W′，假设a′R′b′成立，因为f是一个从W到W′的满射，所以存在a,b∈W使得f(a)=a′并且f(b)=b′。又因R′=f(R)，所以，aRb。因为R在F中是稠密的，所以存在x∈W使得aRx并且xRb。又因R′=f(R)，所以，f(a)R′f(x)并且f(x)R′f(b)成立，即：a′R′x′并且x′R′b′。故：关系R′在F′中是稠密的。

(10)对于任意的a′,b′,c′∈W′，假设b′R′a′并且c′R′a′成立，因为f是一个从W到W′的满射，所以存在a,b,c∈W使得f(a)=a′并且f(b)=b′并且f(c)=c′。又因R′=f(R)，所以，bRa并且cRa。由R在F中是树状的可得：bRc或者cRb成立。因为R′=f(R)，所以f(b)R′f(c)或者f(c)R′f(b)成立，即：b′R′c′或者c′R′b′。故：关系R′在F′中是树状的。

(11)由(3)可得传递性成立。假设在W′中存在如下的元素序列：

因为f是一个从W到W′的满射，所以存在W中的元素aγ∈W(γ<ω)使得f(aγ)=aγ′。又因→′=f(→)，所以有a0→a1→…→aγ→…(γ<ω)，此与已知矛盾。于是，在W′中不存在如下的元素序列：

故：转换关系→′在F′中也是良基的。

推论6 令F=〈W,R〉和F′=〈W′,R′〉是两个框架。若F≅F′，则定理5中的(1)—(11)成立。

证明由F′F′可得：F～F′。利用本节的定理5可得本推论的证明。

定义7 令F=〈W,R〉和F′=〈W′,R′〉是两个框架。令Z⊆W×W′是一个非空二元关系，如果W′的每一个元素w′至少由W中的一个元素w使得wZw′，那么称Z为W到W′的满关系。特别地，当Z是集合W到集合W′上的一个映射时，并且W′的每一个元素w′至少由W中的一个元素w使得wZw′，那么Z叫做W到W′的满射。

定义8 令F=〈W,R〉和F′=〈W′,R′〉是两个框架，令Z⊆W×W′是一个非空二元关系，如果下面的条件成立：

定义9 令F=〈W，R〉和F′=〈W′，R′〉是两个框架，令Z⊆W×W′是一个非空的二元关系，如果下面的条件成立，则称Z是从F到F′的一个互模拟。

(1)如果wZw′并且wRv，那么存在一个v′∈W′使得w′R′v′并且vZv′(向前条件)。

(2)如果wZw′并且w′R′v′，那么存在一个v∈W使得wRv并且vZv′(向后的条件)。

定理10 令F=〈W,R〉和F′=〈W′,R′〉是两个框架。令Z⊆W′W′是一个非空的二元关系，则下面的条件等价：

(1)Z是F到F′的一个模拟；

(2)Z(R)⊆R′，其中Z(R)={Z(w)R′Z(v)|wRv}。

证明(1)⟹(2)。设(Z(w),Z(v))∈Z(R)，因为Z是F到F′的一个模拟，由定义定义8得：如果wZw′并且对所有的v∈W，wRv，那么存在v′∈W′使得w′R′v′并且vZv′。由wZw′得：w′=Z(w)并且由vZv′得：v′=Z(v)。再由w′R′v′得：Z(w)R′Z(v)。故，Z(R)⊆R′。

(2)⟹(1)。如果wZw′并且对所有的v∈W，wRv，可得Z(w)R′Z(v)。取v′=Z(v)，即：w′R′v′并且vZv′。故，于Z是F到F′的一个模拟。

定理11 令F=〈W,R〉和F′=〈W′,R′〉是两个框架。令Z是W到W′的一个非空满的二元关系，则下面的条件等价：

(1)Z是F到F′上的一个互模拟；

(2)Z(R)=R′，其中Z(R)={Z(w)R′Z(v)|wRv}；

证明(1)⟹(2)。因为Z是F到F′上的一个互模拟，由定义9的条件(1)可得：如果wRv，则Z(w)R′Z(v)；由定义9的条件(2)可得：如果Z(w)R′Z(v)，则wRv。

(2)⟹(1)。如果wZw′并且wRv，由(2)可得：Z(w)R′Z(v)。取v′=Z(v)∈W′并且w′=Z(w)，于是，w′R′v′并且vZv′。即：互模拟定义的条件(1)满足。如果wZw′并且w′R′v′，取w′=Z(w)。由于Z是满的，所以对于任意的v′∈W都存在v∈W使得v′=Z(v)。即：Z(w)R′Z(v)。由(2)可得：wRv。于是，互模拟定义的条件(2)满足。

定理12 令F=〈W,R〉和F′=〈W′,R′〉是两个框架，并且令Z是W到W′的一个非空的二元关系，如果Z是F到F′上的一个满模拟，那么Z是F到F′上的一个互模拟。

证明因为Z是F到F′上的一个模拟，由定义8，向前的条件成立；又因为Z是F到F′上的一个满关系，所以对于任意的w′∈W′，都存在一个w∈W使得wZw′成立。如果wZw′并且w′R′v′，那么对于v′取存v∈W使得vZv′成立。因为w′R′v′,即：Z(w)R′Z(v),所以wRv。因此，向后的条件。故，Z是F到F′上的一个互模拟。

由定理12可知：满模拟关系要比互模拟关系强。但是，作者将(另文)利用对应定理证明：在互模拟下，框架F=〈W,R〉具有性质φ当且仅当框架F′=〈W′,R′〉也具有性质φ。

令Z={(a,1),(b,2),(c,3),(d,3),(e,4),(f,5),(f,6)}，下图是框架〈W，R〉到〈W′，R′〉的一个满的互模拟。其中：W={a,b,c,d,e,f}，R={(a,b),(b,c),(b,d),(c,e),(d,e),(e,f)}，W(={1,2,3,4,5,6}，R(={(1,2),(2,3),(3,4),(4,5),(4,6)}。

〈W,R〉 〈W′,R′〉

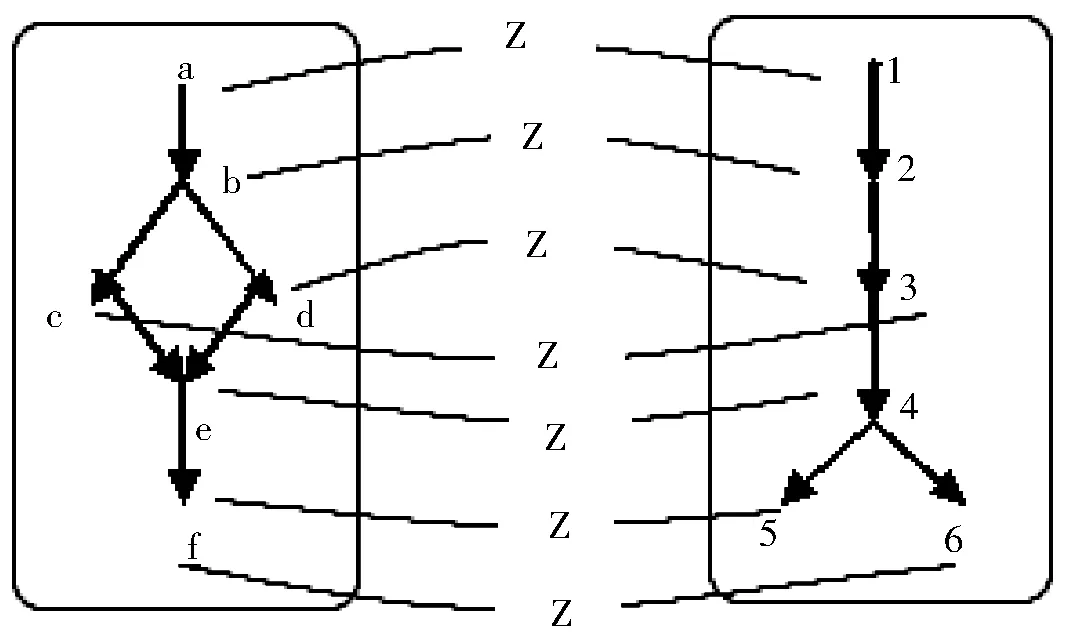
互模拟框架[1]

上图中，Z是W到W′的一个满的关系并且Z(R)={(1,2),(2,3),(3,4),(4,5),(4,6)}=R′。

命题13(不用对应理论) 令F=〈W,R〉和F′=〈W′,R′〉是两个框架。令Z是F到F′的一个满模拟，那么定理5中的(1)—(11)成立。

证明(1)对于任意的w′∈W′，因为Z是F到F′的一个从W到W′的满关系，所以存在w∈W使得wZw′。又因关系R在M中是自返的，所以wRw。由于Z是F到F′的模拟，由定义8，取v′=Z(w)=w′并且w′R′w′。故，关系R′在M′中也是自返的。

(2)对于任意的w′,v′∈W′,假设w′R′v′，因为Z是一个从W到W′的满关系，所以，存在w,v∈W使得wZw′并且vZv′。因为R是对称的，所以，如果wRv，那么vRw。又因为Z是一个模拟，由vZv′并且vRw可得：存在w′∈W′使得wZw′并且v′R′w′。故，关系R′在F′中也是对称的。

(3)对于任意的u′,w′,v′∈W′,假设u′R′w′并且w′R′v′，因为Z是一个从W到W′的满关系，所以，存在u,w,v∈W使得uZu′并且wZw′并且vZv′。因为R是传递的，所以，如果uRw并且wRv，那么uRv。又因为Z是一个模拟，由uZu′并且uRv可得：存在v′∈W′使得vZv′并且u′R′v′。故，关系R′在F′中也是传递的。

(4)由(1)-(3)可得。

(5)对于任意的u′,v′,w′∈W′，假设u′R′v′并且u′R′w′成立，因为Z是一个从W到W′的满关系，所以存在u,v,w∈W使得uZu′并且wZw′并且vZv′。因为R是确定的，所以，如果uRv并且uRw，那么v=w。又因为Z是一个模拟，由uZu′并且uRv(=w)可得：存在v′(=w′)∈W′使得u′R′v′(=w′)。即：v′=w′。故，R′是确定的。

′6)对于任意的w′∈W′,因为Z是一个从W到W′的满关系，所以，存在w∈W使得wZw′。因为R是持续的，所以，对于w∈W，存在u∈W使得wRu。因为Z是一个模拟，由wZw′并且wRu可得：存在u′∈W′使得w′R′u′。故，R′是持续的。

(7)对于任意的u′,v′,w′∈W′，假设u′R′v′并且u′R′w′成立，因为Z是一个从W到W′的满关系，所以存在u,v,w∈W使得uZu′并且wZw′并且vZv′。因为R是欧性的，所以，对于任意的u,v,w∈W，uRv并且uRw⟹vRw或者wRv。因为Z是一个模拟，由vZv′并且vRw可得：存在w′∈W′使得v′R′w′；或者，由wZw′并且wRv可得：存在v′∈W′使得w′R′v′。故，R′是欧性的。

(8)对于任意的x′,a′∈W′，如果a′R′x′成立，因为Z是一个从W到W′的满关系，所以存在x,a∈W使得xZx′并且aZa′。因为R是孤立的，所以，对于任意的x,a∈W，aRx⟹x=a。因为x=a，所以，aRa。因为Z是一个模拟，由aZa′并且aRa可得：存在a′∈W′使得aZa′并且a′R′a′；由xZx′并且xRx可得：存在x′∈W′使得xZx′并且x′R′x′。由x′和a′的任意性可得：x′=a′。故，R′是孤立的。

(9)对于任意的a′,b′∈W′，假设a′R′b′成立，因为Z是一个从W到W′的满关系，所以存在x,a∈W使得aZa′并且bZb′。因为R是稠密的，所以，对于任意的a,b∈W,aRb,存在一个x∈W使得aRx并且xRb。因为Z是一个模拟，由aZa′并且aRx可得：存在x′∈W′使得a′R′x′；由xZx′并且xRb可得：存在b′∈W′使得x′R′b′。于是，任意的a′,b′∈W′，当a′R′b′成立时，存在x′∈W′使得a′R′x′并且x′R′b′。故，R′是稠密的。

(10)对于任意的a′,b′,c′∈W′，如果b′R′a′并且c′R′a′成立，因为Z是一个从W到W′的满关系，所以存在a,b,c∈W使得aZa′并且bZb′并且cZc′。因为R是树状的，所以，对于任意a,b,c∈W，bRa并且cRa⟹bRc或者cRb。因为Z是一个模拟，由bZb′并且bRc可得：存在c′∈W′使得b′R′c′；或者，由cZc′并且cRb可得：存在b′∈W′使得c′R′b′。故，R′是树状的。

(11)对于任意的a0′,a1′,…,aγ′,…∈W′(γ<ω)，如果存在如下的元素序列(ar′|γ<ω)：

由于Z是一个从W到W′的满关系，所以存在a0,a1,…,aγ,…∈W(γ<ω)使得a0Za0′并且a1Za1′并且…并且aγZaγ′…(γ<ω)。即：

Z(a0)→′Z(a1)→′…→′Z(aγ)→′… (γ<ω)

因为Z是一个模拟，由Z(→)⊆→′可得：是良基的，因此，不存在如下的元素序列(ar|(γ<ω)：

a0→a1→…→aγ→… (γ<ω)

此与→是良基的矛盾。故，→′是良基的。

定义14 令F=〈W,R〉和F′=〈W′,R′〉是两个框架。如果W′⊆W，R′是R在W′上的限制′即：R′=R∩(W′×W′)),那么称F′是F的一个子框架。如果F′是F的一个子框架并且对所有的w∈W，下面的条件成立：

如果w∈W′并且Rwv，那么v∈W′，

定义16 令F1=〈W1,R1〉和F2=〈W2,R2〉是两个框架。如果W1∩W2=∅，称框架F1和F2不相交。对于不相交的框架F1和F2，它们的不交并是F1F2=〈W,R〉，这里W=W1∪W2，R=R1∪R2。

命题17 令F1=〈W1,R1〉和F2=〈W2,R2〉是两个框架。如果F1F2，那么定理5中的(1)—(11)成立。其中(11)满足：如果转换关系→在F1F2中是传递的、良基的，那么转换关系→i在Fi中是传递的、良基的(i∈{0,1})。这里→=→1∪→2。

证明(1)对于任意的w1∈W1，因为W=W1∪W2，所以w1∈W并且w1Rw1。因为F1F2，所以，w1R1w1。即：关系R1在F1中是自返的。同理可证：关系R2在F2中是自返的。(2)-(11)的证明也类似。

四、满模拟下的模型性

定义18 设〈W,R〉是任意的框架，V是〈W,R〉上对LPM公式的一个赋值，当且仅当，V是LPM公式集Form(LPM)与W的笛卡尔乘积Form(LPM)(W到集合{0,1}上的映射，即

V：Form(LPM)×W→{0,1}

并且满足下面的条件：对任意的LPM公式φ，φ，ψ和任意的w∈W，

(1)如果φ是命题变项p，那么V(p,w)=1或者V(p,w)=0，且二者只居其一。

(3)如果φ是φ∨ψ，那么V(φ∨ψ,w)=0当且仅当V(φ,w)=0并且V(ψ,w)=0。

(4)如果φ是φ∧ψ，那么V(φ∧ψ,w)=1当且仅当V(φ,w)=1并且V(ψ,w)=1。

(5)如果φ是φ→ψ，那么V(φ→ψ,w)=0当且仅当V(φ,w)=1并且V(ψ,w)=0。

(6)如果φ是◇φ，那么V(◇φ,w)=1当且仅当存在一个w′∈W，若wRw′,则V(φ,w′)=1。

由定义18可得：

V(□φ,w)=1当且仅当对任意的w′∈W，若wRw′,则V(φ,w′)=1。

定义19 令M=〈W,R,V〉和M′=〈W′,R′,V′〉是两个模型，令Z⊆W×W′是一个非空二元关系，如果下面的条件成立：

(1)对所有命题变项p，w∈V(p)当且仅当w′∈V′(p)；

定义20 令M=〈W,R,V〉和M′=〈W′,R′,V′〉是两个模型，令Z是W到W′上的一个非空的二元关系，并且满足定义19中的(1)和(2)以及下面的条件：

对于任意的w′∈W′，都存在一个w∈W使得wZw′成立，

则称Z是从M到M′的一个满模拟。

定理21 令M=〈W,R,V〉和M′=〈W′,R′,V′〉是两个模型，并且令Z是W到W′的一个非空的二元关系，如果Z是M到M′上的一个满模拟，那么Z是M到M′上的一个互模拟。

证明由定义19和定理20可得。

定理22 令M=〈W,R,V〉是任意的非空模型，则它与一个禁自返模型之间存在一个满模

拟。

证明令M=〈W,R,V〉是已知模型，如果M本身是禁自返的，那么取M上的自同构即可。如果M不是禁自返的，那么构造模型M=〈W,R,V〉满足：

(1)W=W+∪W-={w+|对每个w∈W}∪{w-|对每个w∈W}。

(2)R定义为：对每个w∈W，如果Rww，那么Rw+w-和Rw-w+，此时Rw+w+和Rw-w-不成立；对每个w∈W，如果并非Rww，那么Rw+w-和Rw-w+不成立，同时，Rw+w+和Rw-w-也不成立；对任意的w,w′∈W如果Rww′并且w≠w′，那么Rw+w′+,Rw-w′-,Rw+w′-,Rw-w′+。

(3)对所有命题变项p，w∈V(p)当且仅当w+∈V(p)或者w-∈V(p)；

显然，模型M=〈W,R,V〉是禁自返的。现在定义从M到M上的一个关系：

Z={(w,α)|对于任意的w∈W存在α∈W使得σ=w+或者α=w-}，

现在只需验证：Z是从M到M上的一个满模拟。

(1)根据V定义，对于每一个变元p和每一个w∈W，都有w∈V(p)⟺α∈V(p)，这里α=w+或者u=w-，因此Z满足互模拟定义19的条件′1)。

′2)对于任意的w,w′∈W,wZα(α=w+或者α=w-)并且Rww′，如果w=w′，根据R定义可得：Rw+w-和Rw-w+。如果α=w+,则取Rw+w-，并且wZw-成立；如果α=w-，则取Rw-w+，并且wZw+成立。如果w≠w′,并且α=w+，因为Rww′，根据R的定义可得：存在w′+(w′-)并且Rw+w′+(Rw+w′-)，由Z的定义可知：w′Zw′+(w′Zw′-)；如果w≠w′，并且α=w-，因为Rww′，根据R定义可得：存在w′+(w′-)并且Rw-w′+(Rw-w′-)，由Z的定义可知：w′Zw′+(w′Zw′-)。因此，Z是W到W的一个模拟。

(3)由W的定义可知，对于每一个w∈W，都存在α∈W(α=w+或者α=w-)并且wZα，由此可得：Z是W到W上的一个模拟。反之，由Z的构造可知：对于每一个α∈W(α=w+或者α=w-)，存在w∈W并且wZα，由此可得：Z是W到W上的一个满模拟。

推论23 一个模型与一个禁自反模型之间存在一个互模拟。

证明由定理21和22可得。

[1]李娜等.互模拟的一些基本性质[J].云南师范大学学报，2010，(5).

责任编辑：陈 刚

PreservationundertheCircumstanceofFullSimulation

LI Na

With F and F’ as two modes, this paper studies the preservation for f, supposing it as an epimorphis from F to F, as well as some other logic values and transformations in terms of generation, framework and sub-frameworks and features.

epimorphism; full simulation; mutual simulation; disjoint

* 国家社科基金项目“超集、双仿及其在模态逻辑计算机科学中的应用研究”[项目编号：08BZX049]。

B81

A

1003-6644(2016)05-0093-10作者李娜,女,汉族,河南开封人,硕士,南开大学哲学院教授(天津 300350)。