基于分形理论模拟花岗岩崩岗剖面土壤水分特征曲线
2016-10-20邓羽松夏栋蔡崇法王秋霞吕国安丁树文
邓羽松,夏栋,蔡崇法,王秋霞,吕国安,丁树文
(华中农业大学水土保持研究中心,430070,武汉)
基于分形理论模拟花岗岩崩岗剖面土壤水分特征曲线
邓羽松,夏栋,蔡崇法,王秋霞,吕国安,丁树文†
(华中农业大学水土保持研究中心,430070,武汉)
崩岗是我国南方花岗岩地区特殊的土壤侵蚀现象,给山区经济造成了严重的影响。为了探索南方花岗岩地区崩岗侵蚀剖面的水分特性,明确水分与崩岗发育的关系,本研究采用野外调查采样与室内分析的方法,运用土壤粒径分形理论,并结合Brooks and Corey模型,模拟花岗岩崩岗剖面土壤水分特征曲线。选择通城县花岗岩崩岗剖面5个层次(表土层、红土层、过渡层、砂土层和碎屑层)采集土样,通过对土壤粒径分布和土壤含水量的测定,分析分形维数与土壤粒径之间的关系。同时,应用土壤粒径分形理论,模拟土壤水分特征曲线,基于估算结果与实测结果的比较,探讨分形方法估算土壤水分特征曲线的可行性。结果表明:崩岗剖面土壤黏粒质量分数越大,土壤粒径分维值越大;土壤粒径分维值越大,土壤水分特征曲线的分维值则越大,两者之间线性关系较好;运用分形理论,模拟土壤水分特征曲线的预测值与实测值具有良好的一致性,模拟结果的精度随土层的深度增加而增加,模拟效果以土壤黏粒和粉粒质量分数较少、砂粒质量分数较多的土壤效果较好。研究结果为花岗岩崩岗机理的探索奠定了基础,对崩岗水分的研究具有指导意义。
土壤;崩岗;剖面;分形理论;水分特征曲线;南方花岗岩地区
土壤水分特征曲线是描述土壤水吸力与土壤含水量之间的关系曲线,反映了土壤持水性、供水性及水分有效性等基本特性,是定量研究土壤水滞留与运移十分重要的土壤水动力学参数之一[1]。所拟合的水分特征曲线能够反映出土壤的持水性、导水性以及透气性等方面的物理性质,对于水土保持方面的研究具有重要指导意义;但对土壤水分特征曲线的测定,一直以来是比较费时费力的工作。粒径组成对于土壤水分特征曲线存在较大影响,不同质地的土壤水分持有能力有所差别。近年来,引入分形理论,为定量描述土壤粒径分布提供了新途径,分形维数可以表征土壤粒径分布的差异和自相似性,并反映其均匀程度[2-3]。F.Bartoli等[4]发现土壤质地和结构,如容重、孔隙度以及粒径等物理性状均表现出分形特征,同时,对于土壤的水力参数存在直接或者间接的影响。
结合土壤分形理论,对土壤水分特征曲线进行预测的研究也有相关报道。2002年,黄冠华等[5]应用Menger海绵结构模型,推导出包含有分形维数的土壤水分特征曲线的解析模型。之后,刘建立等[6]、苏里坦等[7]、王展等[8]、程东兵等[9]以及郑子成[10]等研究不同的土壤,采用土壤粒径分形维数或者土壤颗粒数量分形维数,预测土壤水分特征曲线,结果均体现了可行性。而对于花岗岩风化发育的土壤水分特征曲线,目前还尚未见报道,同时,对于花岗岩地区常见的土壤侵蚀现象—崩岗的研究关注较多,崩岗发生暴露了花岗岩的剖面,剖面土壤的性质对于土壤水分有不同的影响。中国南方崩岗的发育范围之广、面积之大给农业带来了无法估量的威胁[11-16],而对于崩岗剖面水分方面的研究较少;因此,基于土壤水分特征曲线的应用以及测量的难题,本文采用土壤粒径分形理论,模拟花岗岩地区崩岗剖面土壤水分特征曲线,拟通过本研究为崩岗水分的探索提供依据。
1 分形模型
描述自然界复杂的构型一直是传统数学的难题,近年来,分形理论的产生为研究这类复杂的对象,找到了全新的方法和思路,因而引入分形维数来描述这些复杂事物特征。土壤本身是一种具有自相似结构的多孔介质,研究者对其结构不断探索,早在1986年,D.L.Turcotte[17]提出土壤分形,可用颗粒粒径与数量的关系来定义
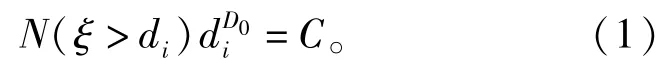
式中:di为第i个粒径;N(ξ>di)表示粒径大于di的土壤颗粒总数;D0为土壤粒径数目分布的分形维数;C为与土壤性质相关的常数。
实际上,不管是采用吸管法,还是利用激光粒度仪等仪器,均不能直接通过实验得出土壤颗粒总数。本研究以吸管法测定土壤粒径分布,其结果均为粒径质量的分布值。1993年,杨培岭等[18]提出的用土壤粒径的质量分布表征分形特征,为研究土壤粒径分形特征建立了新的领域
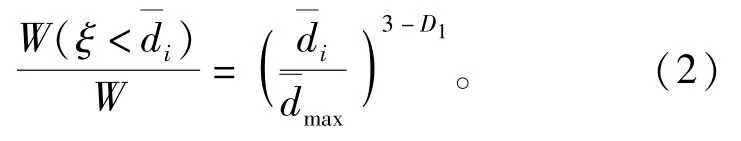
1990年,S.W.Tyler等[19]根据前人提出的分形理论,推导出土壤水分特征曲线的分形模型
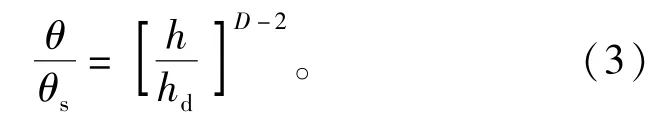
式中:θ为体积含水量;θs为土壤饱和含水量;h为土壤水吸力;hd为进气吸力;D为土壤的孔隙体积分形维数。将模型推广到三维欧氏空间,公式转换成为

拟合土壤水分特征曲线的模型较多[20],各个模型的拟合效果也有区别。其中,Brooks and Corey模型表达式为

式中:λ为拟合参数。通过观察,公式(3)、(4)、(5)形式上基本一致,通过公式(4)、(5)不难发现:λ=3-D。公式(4)从孔隙介质的结构方面阐述了含水量和基质吸力的关系,从而使模型(5)有了物理意义。
2 材料与方法
2.1供试土样
供试土样为燕山期发育的花岗岩红壤,取自湖北通城(E 113°36'~114°4',N 29°2'~29°24')崩岗侵蚀区土体剖面。通城是我国崩岗发育的北缘区,崩岗侵蚀严重,土壤侵蚀模数大。本研究选择通城五里村崩岗剖面,其发育规律符合我国南方花岗岩区崩岗的典型特征。通过对土壤剖面颜色、植被根系等特征,来确定发生层,剖面自上而下分为5个层次,分别为表土层、红土层、过渡层、砂土层和碎屑层。针对5个层次采集散土,经风干,并过2mm筛后,采用吸管法测定土壤颗粒组成,土壤厚度、粒径分析以及土壤质地分类如表1所示。同时,用仪器配置的离心环刀,采集剖面土样,用于水分特征曲线的测定,每个层次4个重复。
2.2土壤水分特征曲线的测定
使用HITACHI公司制造的CR21G高速恒温离心机测定土样,采取离心法测定土壤水分特征曲线,将装有原土的离心环刀,在水中浸泡24 h直至饱和。设定0.01、0.02、0.03、0.05、0.1、0.5、1.0和1.5MPa共8个吸力。实验过程中,设定离心机测定温度为恒温20℃,求得相应条件下对应的土壤体积含水量,得到土壤水分特征曲线。
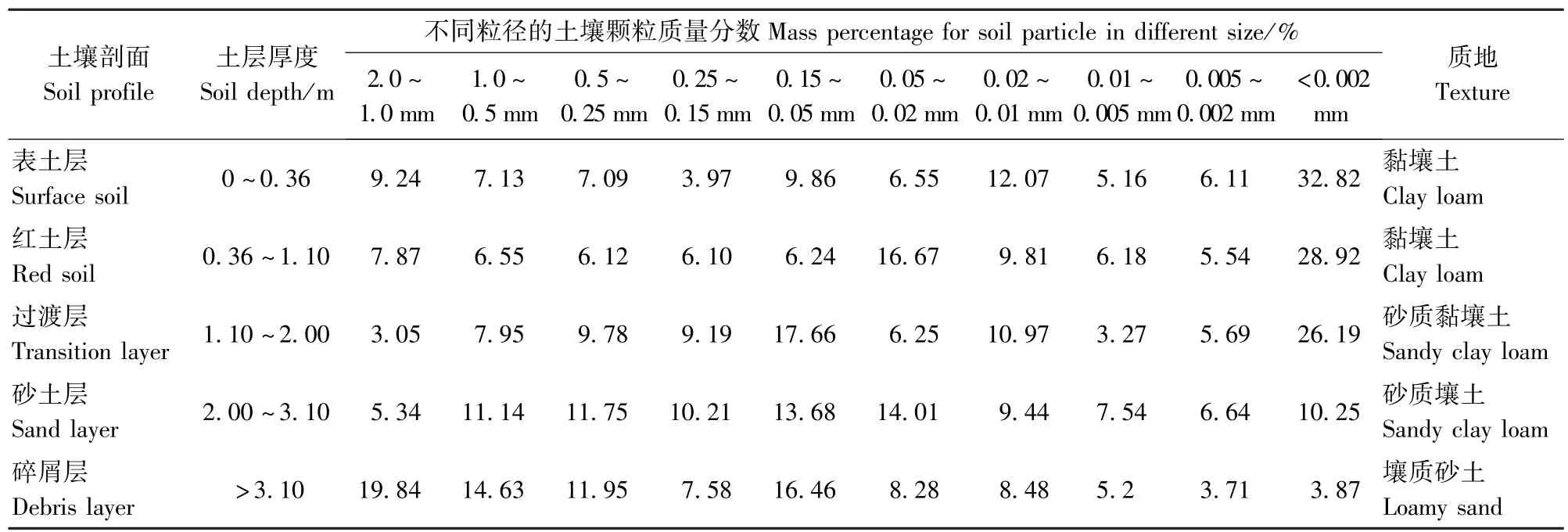
表1 供试土壤粒径分析Tab.1 Analysis of particle size for the studied soil
以均方差RMSE来检验预测方法的准确性,计算公式定义为
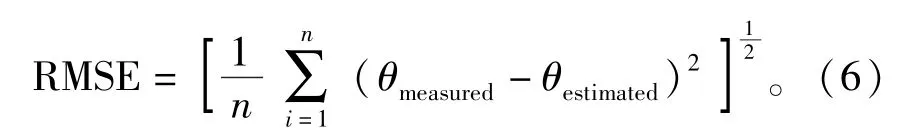
式中:n为实测水分质量分数的个案数;θmeasured为水分质量分数实测值;θestimated为分形模型计算的水分质量分数预测值。
3 结果与分析
3.1土壤粒径分形维数的拟合
表2中土壤粒径分形维数是根据模型式(2)计算得出,具体做法_结合表1土壤不同粒径质量分数,分别以为纵坐标和横坐标绘图,以最小二乘法线性回归分析,计算得到质量分形维数D1值,所得相关系数均在0.9以上,线性相关达到极显著(P<0.01)。同时,通过实测的花岗岩崩岗剖面的5个层次土壤水分特征曲线数据,结合Brooks and Corey模型,以最小二乘法进行回归分析,计算出土壤水分特征曲线的分形维数D值,同时,土壤饱和含水量θs和进气吸力hd值也可以由此拟合,推导出表2。
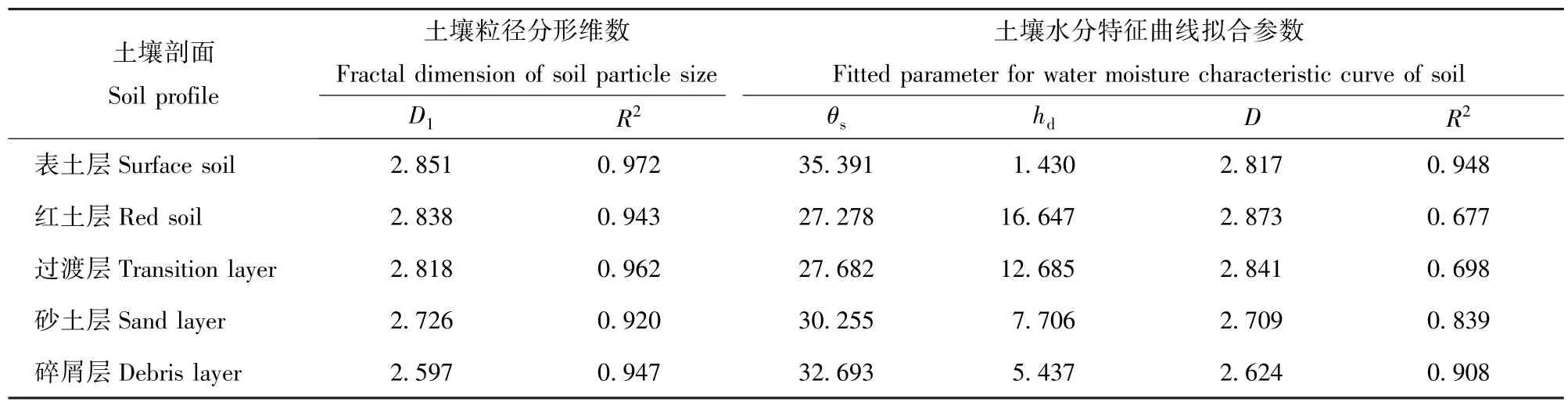
表2 土壤粒径的分形维数Tab.2 Fractal dimension of soil particle size
由表1可知,花岗岩风化剖面,土壤颗粒呈现自表土层向碎屑层砂粒不断增加的趋势,<0.002mm的黏粒质量分数呈逐渐减少的趋势,表土层黏粒质量分数占32.87%,而碎屑层黏粒质量分数仅有3.87%。结合表2不难发现,分形维数D1、D与<0.002mm的黏粒,呈现很显著的正相关关系,相关性系数分别为0.963和0.939。也就是说,土壤细颗粒物质越多,分形维数值就越高。同时,土壤粒径分形维数D1与土壤水分特征曲线分形维数D十分接近,值域分别在2.597~2.851和2.624~2.873之间。从计算结果来看,土壤这种多孔介质的结构性质,具有统计学的意义,能表现出比较明显的分形特点。从土壤的角度来说,黏粒质量分数多,则土粒间胶结效果好;黏粒质量分数少,则容易受到水的冲蚀;因此,下土层容易被冲蚀,而造成上土层悬空形成龛[21],龛的不断崩塌,溯源侵蚀容易形成崩岗,这是花岗岩风化区容易发生崩岗的原因之一。同时,也说明了土壤粒径分形维数和土壤水分特征曲线分形维数,均能很好地反映花岗岩崩岗剖面的抗蚀性。
从土壤质地方面来看,由表1可知,花岗岩不同层次的土壤质地不同,其拟合的分形维数不同,分维值由小到大依次为:壤质砂土<砂质壤土<砂质黏壤土<黏壤土。这说明分形维数值的大小与土壤质地密切相关,土壤黏粒质量分数越高,分形维数值则越大。而从土壤粒径分形维数D1与土壤水分特征曲线分形维数D方面,容易发现两者之间的变化趋势基本上一致,对两者进行线型回归分析可知:
D=0.932 5D1+0.193 6,R2=0.918 6。(7) 3.2 土壤水分特征曲线预测
通过线性回归分析,可以明确土壤粒径分形维数D1与土壤水分特征曲线分形维数D的关系式(7),将其代入水分特征曲线进行预测,可以得到预测值①,以D1直接代替土壤水分特征曲线分形维数D值进行预测,可以得到预测值②。同时,将水分特征曲线的拟合值、预测值①和预测值②与实测值进行对比,通过公式(6)计算均方差RMSE。
从图1(a)可以看到,花岗岩崩岗剖面表土层土壤水分特征曲线预测值①和预测值②具有一致性,但与实测值偏差较大。结合表3可知:均方差分别达0.024 4和0.025 2,以土壤粒径分形维数D直接预测水分特征曲线,误差相对较小;但在低吸力段预测的效果较好,Brooks and Corey模型拟合曲线效果最好。这可能是由于分析时忽略了土壤的团聚作用,需要进一步进行研究。而对于花岗岩的红土层(图1(b)),预测值②的模拟效果优于预测值①,预测值①的均方差为0.020 2,预测值②的均方差为0.019 6,但预测值对于高吸力段的模拟效果趋势较好。图1(c)显示:用预测值模拟过渡层水分特征曲线的效果,明显比表土层和红土层好,预测值①、预测值②和拟合值的均方差接近,分别为0.017 9、0.017 3和0.015 4,说明用土壤粒径分形维数模拟水分特征曲线,与Brooks and Corey模型拟合的效果相近。砂土层(图1(d))土壤在低吸力的情况下,预测值比模拟拟合的效果好,与实测值能够基本吻合,预测值①和预测值②的均方差分别为0.014 5和0.016 1,表明预测值①的效果比预测值②的模拟效果好,跟Brooks and Corey模型拟合的效果相近。从整个花岗岩崩岗剖面来看,预测效果最好的层次为碎屑层,该层次土壤分形维数最小,粗颗粒最多而黏粒最小,分形特征最为明显。从图1(e)来看,预测值①和预测值②与Brooks and Corey模型拟合的曲线基本能够达到一致,预测值①和预测值②的均方差分别为0.012 6和0.010 6,拟合值的均方差为0.010 3,预测效果最佳,说明利用土壤粒径分形维数,预测水分特征曲线的方法可行。此外,通过拟合土壤基质吸力与水分的实测数据可以发现,Brooks and Corey模型对于拟合花岗岩崩岗剖面土壤水分特征曲线均方差较小,平均值仅为0.011 5,说明Brooks and Corey模型能够用于花岗岩土壤水分特征曲线的拟合。
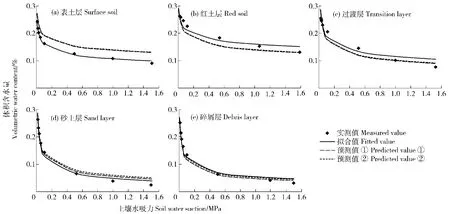
图1 土壤水分特征曲线的实测值、拟合值与预测值的比较Fig.1 Comparison of themeasured values,fitted values and predicted values in soilmoisture characteristic curve
由表3可推出,预测值①和预测值②对于花岗岩土壤水分特征曲线的模拟效果相似,均方根误差值的偏差都在0.002以内。同时,针对土壤剖面每个层次预测值的均方根误差进行分析,预测值①和预测值②的平均均方根误差值,自表土层至碎屑层分别为0.024 8、0.019 9、0.017 6、0.015 3和0.011 7,从数据分析可知,模拟效果在花岗岩剖面下层更好,并且自上而下逐渐变好,模拟值与实测值更加接近,图1的拟合曲线很直观反映了这一现象;同时,也说明用土壤粒径分形维数模拟水分特征曲线有良好的效果:因此,对于当前土壤水分特征曲线测定过程的复杂性,利用土壤颗粒组成直接进行预测,能够节约人力以及物力等资源。主要用来研究无规则图形以及复杂的结构特征。分形维数是分形理论具体的表现方式,通过分形维数,不仅能够比较不同土壤的颗粒分布规律和质地均匀程度,还可以用来反映土壤的土壤肥力以及土壤退化程度[23]。本文将花岗岩崩岗地区,土壤的粒径分形维数与土壤水分特征曲线联系在一起,用粒径分形维数值,推导水分特征曲线的可行性。从分形维数的角度来看,花岗岩土体由表层向下分形维数逐渐减小,即土壤的质地越细,分维值越高,其关系跟土壤粒径分形维数的大小与土壤质地的关系一致[5]。水分特征曲线是模拟土壤中,水分与溶质运移关系最重要的物理参数。研究土壤水分特征曲线,可以反映土壤的水分、孔隙状况,间接提供灌溉的依据,明确土壤的透气性质。通过对不同的土壤进行水分质量分数与基质吸力的关系研究,均反映了水分质量分数随着基质吸力的增加而减少,同时,也与土壤物理性质有一定相关性[24-27]。本文得出的花岗岩崩岗土壤的水分变化趋势与前人研究结果一致;与此同时,从不同层次的土壤看,发现砂土层和碎屑层的水分特征曲线释水性明显大于其他土层,可能是由于颗粒组成中砂粒质量分数较大,导致崩岗表土层和红土层对水分吸力极强,而疏松的砂土层和碎屑层水分变化快,吸水能力弱。基于土壤水分特征曲线的测定方法复杂、耗时和费力,如本实验中采用的离心机测定量少、需要的时间较长,使得获取大区域、大量参数不可行,同时,土壤质地的空间结构变异性影响到实验精度[7],因而需要探索
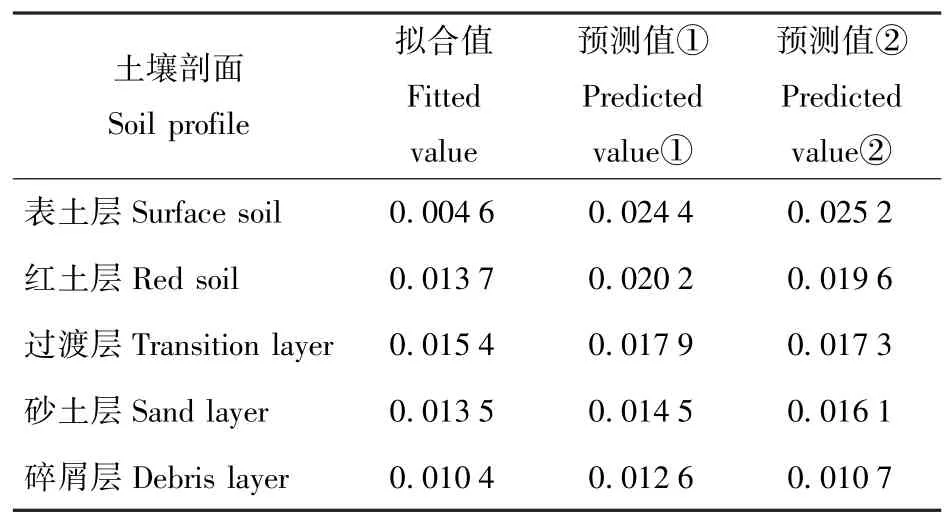
表3 土壤含水量拟合与预测误差(RMSE)Tab.3_Fitted and predicted error of soilwater content(RMSE)
4 讨论
1983年,B.B.Mandelbrot提出了分形理论[22],更为简便的方法。本文通过一组实测的土壤水分质量分数与基质吸力值,并以Brooks and Corey模型拟合建立水分特征曲线,同时,通过分形维数值进行模拟。同样的方法,目前也引起部分研究者的探讨。苏里坦等[7]运用塔里木河干流两岸土壤粒径分维值推导水分特征曲线,所计算的粒径分维值、水分特征曲线分维值与本文所计算的非常接近。同时,张杰等[28]采用同样的方法,对鲁中南山地典型植被下土壤得到了类似结论,误差范围较小。程东兵等[9]利用粒径数量与粒径质量的分形维数,分别推导紫色土水分特征曲线,相对本文研究分维值模拟花岗岩土壤水分特征曲线模拟效果稍好,均方差基本小于本文RMSE值;但通过研究花岗岩土壤的模拟情况,模拟效果自上层土壤至下层逐渐变好。可能是由于下层的土壤颗粒质量分数增加,分形特征比上层明显,黏性土壤中含水率分布不均匀,砂性土壤因其孔隙大小较一致,而其含水率的变化不大,土壤水张力的实测值与预测值十分接近,因而模拟效果较好。这与苏里坦等[7]研究一致。崩岗剖面的理化性质差异性较大,通过研究剖面土壤粒径分形维数和水分特征曲线,发现土壤性质之间具有密切的联系;因此,本文基于分型理论模拟土壤水分特征曲线的研究,发现其可行性之后,可以应用到崩岗区域的探索[29-30],花岗岩风化区崩岗发育旺盛,面积较大,通过水分特征曲线,可以掌握其土壤物理特性。总体上来说,以上花岗岩5个层次的土壤水分特征曲线的预测值与模拟值比较接近,表明模型的预测结果能够模拟实测的土壤水分特征曲线。研究结果对于崩岗研究中,以土壤颗粒大小分布的分形维数来模拟土壤水分特征曲线,有重要的指导意义。
5 结论
1)花岗岩崩岗剖面土壤粒径分形维数值介于2.597~2.851之间,由于土壤粒径的拓扑是2,因此,分形维数增值在0.597~0.851之间,而土壤水分特征曲线的拟合分形维数值介于2.624~2.873之间,分形维数增值在0.624~0.873之间,两方面变化趋势基本一致。同时,土壤水分特征曲线的分形维数值与粒径分形维数值存在线性关系,粒径分维值越高,水分特征曲线分维值则越高。分形维数的大小与土壤质地密切相关。随土壤质地从表土层的黏壤土到碎屑层的砂质壤土,其土壤粒径的分形维数逐渐减小。体现分形维数值随着砂粒增加而减小,而随着细颗粒增加而增大。
2)本研究采用Brooks and Corey模型,拟合建立水分特征曲线,同时,建立了花岗岩崩岗剖面土壤水分特征曲线预测的分形模型。将预测模型应用到花岗岩崩岗土壤中,结果表明,土壤水分特征曲线的预测结果与实测值具有良好的一致性,同时,模拟效果沿着土层向下逐渐增强,对于碎屑层的土壤预测效果最好。总体而言,利用土壤粒径分形维数,预测水分特征曲线分形模型,为花岗岩崩岗土壤水分特性曲线的确定,提供了一种简便实用的方法。
[1] 邵明安,王全九,黄明斌.土壤物理学[M].北京:高等教育出版社,2006:67-79. Shao Mingan,Wang Quanjiu,Huang Mingbin.Soil physics[M].Beijing:Higher Education Press,2006:67-79.(in Chinese)
[2] 白一茹,汪有科.黄土丘陵区土壤粒径分布单重分形和多重分形特征[J].农业机械学报,2012,43(3): 43. Bai Yiru,Wang Youke.Monofractal and multifractal analysis on soil particle distribution in hilly and gully areas of the loess plateau[J].Transactions of the Chinese Society for Agricultural Machinery,2012,43(3):43.(in Chinese)
[3] Huang Guanhua,Zhang Renduo.Evaluation of soilwater retention curve with the pore-solid fractal model[J]. Geoderma,2005,127(1/2):52.
[4] Bartoli F,Philippy R,Doirisse M,et al.Structure and self-similarity in silty and sandy:the fractal approach [J].Soil Science,1991,28(42):167.
[5] 黄冠华,詹卫华.土壤水分特性曲线的分形模拟[J].水科学进展,2002,13(1):55. Huang Guanhua,Zhan Weihua.Modeling soil water retention curve with fractal theory[J].Advances in Water Science,2002,13(1):55.(in Chinese)
[6] 刘建立,徐绍辉.根据颗粒大小分布估计土壤水分特征曲线:分形模型的应用[J].土壤学报,2003,40 (1):46. Liu Jianli,Xu Shaohui.Figuring soil water characteristic curve based on particle size distribution data:application of fractalmodels[J].Acta Pedologica Sinica,2003,40 (1):46.(in Chinese)
[7] 苏里坦,张展羽.塔里木河干流两岸土壤水分特征曲线的分形模拟[J].干旱区地理,2005,27(4):530. Su Litan,Zhang Zhanyu.Fractalmodel for predicting the curves of unsaturated soil water retention along themainstream of the Tarim river[J].Arid Land Geography,2005,27(4):530.(in Chinese)
[8] 王展,周云成,虞娜,等.以分形理论估计棕壤水分特征曲线的可行性研究[J].沈阳农业大学学报, 2006,36(5):570. Wang Zhan,Zhou Yuncheng,Yu Na,et al.Feasibility reaserch on estimating the soil water retention curve of brown earth with fractalmethod[J].Journal of Shenyang Agricultural University,2006,36(5):570.(in Chinese)
[9] 程冬兵,蔡崇法,彭艳平,等.根据土壤粒径分形估计紫色土水分特征曲线[J].土壤学报,2009,46 (1):30. Cheng Dongbing,Cai Chongfa,Peng Yanping,et al.Estimating soilwater retention curve based on fractal dimension of soil particle size distribution of purple soil[J]. Acta Pedologica Sinica,2009,46(1):30.(in Chinese)
[10] 郑子成,李卫,李廷轩,等.基于分形理论的设施土壤水分特征曲线研究[J].农业机械学报,2012,43 (5):49. Zheng Zicheng,LiWei,Li Tingxuan,et al.Soil water retention curve based on fractal theory in greenhouse soil [J].Transactions of the Chinese Society for Agricultural Machinery,2012,43(5):49.(in Chinese)
[11] 邓羽松,丁树文,邱欣珍,等.赣县崩岗洪积扇土壤肥力的空间分异规律[J].中国水土保持科学,2014,13 (1):47. Deng Yusong,Ding Shuwen,Qiu Xinzhen,et al.Spatial distribution of collapsing alluvial soil fertility in Ganxian county,Jiangxi province[J].Science of Soil and Water Conservation in China,2014,13(1):47. (in Chinese)
[12] Xu Jiongxin.Benggang erosion:the influencing factors [J].Catena,1996,27(3):249.
[13] 刘希林,张大林.基于三维激光扫描的崩岗侵蚀的时空分析[J].农业工程学报,2015,31(4):204. Liu Xilin,Zhang Dalin.Temporal-spatial analyses of collapsed gully erosion based on three-dimensional laser scanning[J].Transactions of the Chinese Society of Agricultural Engineering,2015,31(4):204.(in Chinese)
[14] 邓羽松,丁树文,蔡崇法,等.鄂东南崩岗洪积扇土壤物理性质空间分异特征[J].中国农业科学,2014, 47(24):4850. Deng Yusong,Ding Shuwen,Cai Chongfa,et al.Spatial distribution of the collapsing alluvial soil physical properties in southeastern Hubei[J].Scientia Agricultura Sinica,2014,47(24):4850.(in Chinese)
[15] Gong JG,Jia YW,Zhou ZH,et al.An experimental study on dynamic processes ofephemeralgully erosion in loess landscapes[J].Geomorphology,2011,125(1): 203.
[16] 张晓明,丁树文,蔡崇法.干湿效应下崩岗区岩土抗剪强度衰减非线性分析[J].农业工程学报,2012, 28(5):241. Zhang Xiaoming,Ding Shuwen,Cai Chongfa.Effects of drying and wetting on nonlinear decay of soil shear strength in slope disintegration erosion area[J].Transactions of the Chinese Society of Agricultural Engineering,2012,28(5):241.(in Chinese)
[17] Turcotte D L.Fractals and fragmentation[J].Journal of Geophysical Research,1986,91(B2):1921.
[18] 杨培岭,罗远培,石元春.用粒径的重量分布表征的土壤分形特征[J].科学通报,1993,38(20):1896. Yang Peiling,Luo Yuanpei,Shi Yuanchun.Fractal characteristics of soil by weight distribution of particle size[J].Chinese Science Bulletin,1993,38(20):1896. (in Chinese)
[19] Tyler SW,Wheatcraft SW.Fractal processes in soil water retention[J].Water Resources research,1990,26 (5):1047.
[20] Kosugi K.Lognormal distribution model for unsaturated soil hydraulic properties[J].Water Resources research, 1996,32(9):2697.
[21] 丁树文,蔡崇法,张光远.鄂东南花岗地区重力侵蚀及崩岗形成规律的研究[J].南昌工程学院学报, 1995,(增1):50. Ding Shuwen,Cai Chongfa,Zhang Guangyuan.A study on gravitational crosion and the formation of collapse mound in the granite area of southeast Hubei[J].Journal of Nanchang College of Water Conservancy and Hydroelectric Power,1995,(S1):50.(in Chinese)
[22] Mandelbrot B B.The fractal geometry of nature[M]. San Francisco:W H Freeman,1991,51(3):286.
[23] 伏耀龙,张兴昌,王金贵.岷江上游干旱河谷土壤粒径分布分形维数特征[J].农业工程学报,2012,28 (5):120. Fu Yaolong,Zhang Xingchang,Wang Jingui.Fractal dimension of soil particle-size distribution characteristics in dry valley ofupperMinjiang river[J].Transactions of the Chinese Society of Agricultural Engineering,2012, 28(5):120.(in Chinese)
[24] Oh S,Lu N,Kim Y K,etal.Relation between the soil water characteristic curve and the suction stress characteristic curve:experimental evidence from residual soils [J].Journal of Geotechnical and Geoenvironmental Engineering,2012,138(1):47.
[25] Hwang S I,Powers SE.Estimating unique soil hydraulic parameters for sandy media from multi-step out flow experiments[J].Advances in Water Resources,2003, 26(4):445.
[26] 王丽琴,李红丽,董智,等.黄河三角洲盐碱地造林对土壤水分特性的影响[J].中国水土保持科学, 2014,12(1):38. Wang Liqin,LiHongli,Dong Zhi,etal.Effectofafforestation on soil moisture characteristics of saline-alkali soil in the Yellow River Delta[J].Science of Soil and Water Conservation,2014,12(1):38.(in Chinese)
[27] 邓羽松,丁树文,刘辰明,等.鄂东南花岗岩崩岗崩壁土壤水分特征研究[J].水土保持学报,2015,29 (4):132. Deng Yusong,Ding Shuwen,Liu Chenming,et al.Soil moisture characteristics of collapsing gully wall in granite area of southeastern Hubei[J].Journal of Soil and Water Conservation,2015,29(4):132.(in Chinese)
[28] 张杰,高鹏,孙会敏,等.鲁中南山地典型植被土壤颗粒与土壤水分特征曲线的分形学特征[J].中国水土保持科学,2013,1(1):75. Zhang Jie,Gao Peng,Sun Huimin,et al.Fractal characteristics of soil particles and soil water retention curve under typical vegetations in mountainous land of central southern Shandong[J].Science of Soil and Water Conservation,2013,1(1):75.(in Chinese)
[29] Xia Dong,Deng Yusong,Wang Shuling,et al.Fractal features of soil particle-size distribution of different weathering profiles of the collapsing gullies in the hilly granitic region,south China[J].Natural Hazards, 2015,79(1):455.
[30] 邓羽松,李双喜,丁树文,等.鄂东南崩岗不同层次土壤分形特征及抗蚀性研究[J].长江流域资源与环境,2016,25(1):63. Deng Yusong,Li Shuangxi,Ding Shuwen,et al.Research on different soil layers of collapsing gully fractal characteristics and erosion characteristics in Tongcheng [J].Resources and Environment in the Yangtze Basin, 2016,25(1):63.(in Chinese)
Simulation of water characteristic curve in the soil profile of the collapsing gully on granite area of South China based on the fractal theory
Deng Yusong,Xia Dong,Cai Chongfa,Wang Qiuxia,Lyu Guoan,Ding Shuwen
(Research Center ofWater and Soil Conservation,Huazhong Agricultural University,430070,Wuhan,China)
[Background]Collapsing gully,a serious soil erosion phenomenon in granite areas of South China,occursmainly on mound or hill slopes under the interaction of water and gravity,causing severe destructions and threats in a wide range,including Hubei,Hunan,Jiangxi,Anhui,Fujian,Guangdong, and Guangxi,mainly south to the Yangtze River,and hence a grave impact on the economy in these hilly regions.[M ethods]In order to explore the relationship between the soilmoisture and the developmentof the collapsing gully,a field survey and indoor analysis were used to investigate the relationship between the soilmoisture and the collapsing gully.The soilwater characteristic curve of granitewas simulated by fractal theory with Brooks and Corey model.The samples of profile(surface soil,red soil,transition layer,sand layer,and debris layer)in granite collapsing gully of Tongcheng County were collected,and the relationship between fractal dimension and soil particle size were analyzed by measuring the soil particle size distribution and soilmoisture content.At the same time,the fractal theory of soil particlesize was applied to simulate the soil water characteristic curve.Further,based on a comparison of estimated and measured results,the feasibility of estimating the soil water characteristic curve by fractal theory was explored.[Results]The higher the soil clay content in the profile of collapsing gully was,the larger the fractal dimension of soil particle size was;the larger the fractal dimension of soil particle size was,the larger the fractal dimension value of soilwater characteristic curve was,indicating that there was a solid linear relationship between the two;the predicted values from the simulation of soil water characteristic curve by the fractal theory and measured values were in fine consistence,the accuracy of simulation results increased with the depth of soil increasing.The simulation effectwas better for the soil containing less soil clay and silt content and more sand content.[Conclusions]The research results lay a foundation for the exploration of themechanism of granite collapsing gully,which provides the guiding significance for the study of the water in collapse gully.
soil;collapsing gully;profile;fractal theory;water characteristic curve;granite area of South China
S152.7
A
1672-3007(2016)02-0001-08
10.16843/j.sswc.2016.02.001
2015-09-07
2016-01-19
项目名称:国家自然科学基金“花岗岩红壤优先流及其与崩岗侵蚀发育的关系”(41571258);国家科技支撑计划子课题“红壤崩岗侵蚀区农田质量保护与崩岗治理技术与示范”(2011BAD31B04)
邓羽松(1988—),男,博士研究生。主要研究方向:水土保持与环境生态。E-mail:dennyus@163.com
简介:丁树文(1964—),男,副教授,硕士生导师。主要研究方向:水土保持与农业生态。E-mail:dingshuwen@ mail.hzau.edu.cn
