K进制遗传算法在聚类问题求解中的应用

韩　海

（江汉大学 数学与计算机科学学院，湖北　武汉　430056）

K进制遗传算法在聚类问题求解中的应用

韩海

（江汉大学 数学与计算机科学学院，湖北武汉430056）

文章提出了用K进制串作为遗传算法的染色体的方案，给出了用该算法求解聚类问题的一般性步骤，并对该方法的适用性进行了分析。

聚类；遗传算法；K进制串；染色体

尽管计算机在重复计算方面具有人类无法比拟的速度，但在处理高复杂度的问题时，穷举法随着数据量的增长仍然会很快失效。有着广泛应用的聚类问题是典型的高复杂度问题、TSP问题［1］、Web文档聚类［2］是其中的典型应用。穷举法可以确保找出问题的最优解，但在面对计算量巨大的聚类问题时，穷举法显得无能为力。为此，遗传算法、蚁群算法、粒子群算法、退火算法等应运而生，这些算法都是在解空间内做部分搜索，在可以接受的时间内找出已搜索到最优解，并以此作为原问题的解。

1　遗传算法与聚类问题

遗传算法（Genetic Algorithm）是一种通过模拟生物进化过程搜索最优解的方法。它模拟生物进化过程中的自然选择和遗传机理，能较好地在解空间中进行搜索。遗传算法首先需要有一个由若干个生物体构成的种群，每个个体都包含有一组特定的信息，称为染色体。染色体具有相同的结构。遗传就是由当前种群把染色体所包含的信息按一定规则传递给下一代。传递规则既保证了对当前种群的择优，也保证了适应性较差的个体也能有一定的遗传机会。遗传算法的流程如图1所示。

聚类是根据数据之间的联系紧密程度把一个数据集划分成若干个子集，每个子集称为一个簇，使得在同一簇内的数据联系紧密，而处于不同簇内的数据之间联系疏松。通常用簇内距离表示簇内数据的聚集程度，用簇间距离表示簇与簇之间有一定的差异，并且以这两个参数的某种综合计算作为度量一个划分优劣的指标。

设数据集中共有n个样本，记作S1，S2，S3，…Sn，规定最多聚成k个类，如果用穷举法针对每一种可能的划分进行比较、筛选，其计算量是O（kn），因而不得不采取一些措施，用遗传算法是一个很好的方案。

2　求解聚类问题的步骤

遗传算法通常都采用定长的2进制位串作为染色体，以保证任意位串都是问题的一个解，而最优解显然是其中的一个或多个特定的位串。2进制在多数情况下可以简化编程，但并不是唯一选择。针对聚类问题，采用K进制的染色体更简洁。

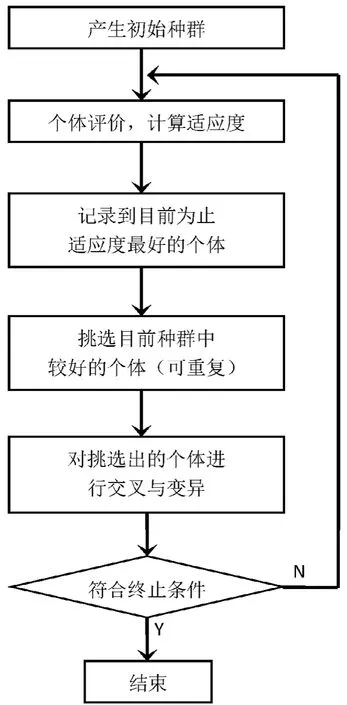
图1　遗传算法的流程示意

不妨把染色体设计成一个长度为n的K进制数，即：

C1C2C3C4Cn

其中Ci（i=1，2，3，…n）是1位K进制数，在0～k-1取值，表示第i个样本归属于第Ci号簇。再令种群的数目为m，于是，遗传算法的各个步骤都有相应的进行处理方法：

（1）初始化。可创建m×n的数组，记作W，并把数组每个元素赋值为一个0到k-1之间的随机值。以W［i］［j］表示第i号染色体第j个位置的值，设该值为x，则表示按照第i号染色体划分子集时第j号样本应归属于x簇。

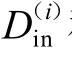
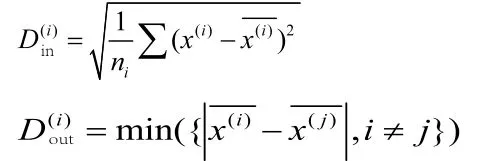
其中ni是第i个簇中的样本个数，X（i）表示第i簇中的一个样本，簇的中心之间的距离。一个个体的适应度是各个簇的是第i个簇的中心，｜X（i）-X（j）｜表示第i个簇与第j个除以再求和。

（3）记录最优个体。简单的求最小值问题。

（4）挑选较优个体。这是生成下一代种群的第一步。挑选的方法较多，但总的原则都是令适应度较好的个体优先被选中。不妨先将种群中的m个个体按适应度排序，对适应度好的个体赋以较大的权值，经实验，可以令第i个个体的权值为（m-i）^2。然后做m次循环，每次产生一个m^2以内的随机数x，对（m-i）^2>=x求最大i值，即本次循环选中的是第i个个体。

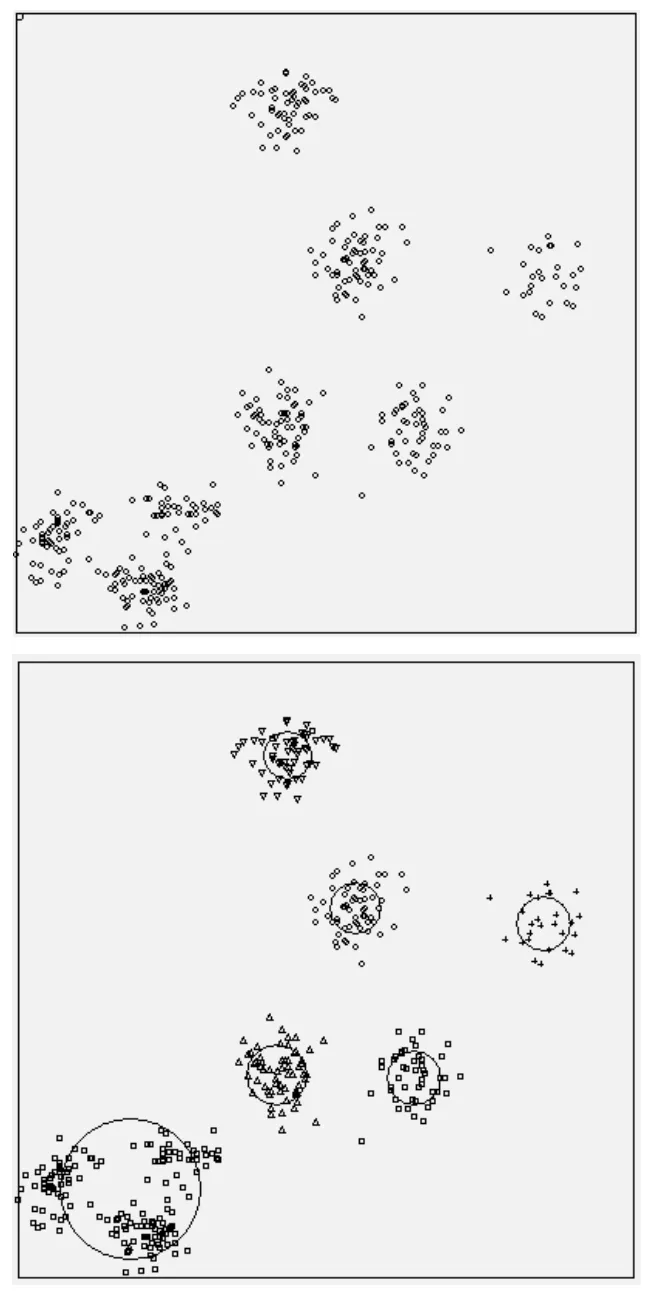
（5）交叉与变异。设置一个固定值Ta，0<=Ta<=m，针对前Ta个个体以两两配对的方式进行染色体交叉，以一个随机的位置为界，两个染色体交换后一半；再设置一个固定值Tb，0

不妨以固定次数的循环进行控制，不论设置循环次数为多少，循环终止时都可以得到一个本次搜索的最优解。遗传算法本身决定了找到的是一个比较好的解，但不保证是最优解。

3　效果分析

对于n个数据的样本集，通常规定聚成不超过m个类，总是有m

在一台主频为3.4G的普通个人电脑上以VC环境编程实现上述算法，可以在以秒计的时间内解决数百个样本、数千次循环的聚类问题。如图2所示，是以400个仿真数据进行实验的效果。

图2　400个仿真数据进行实验的效果

当然，用上述算法求解聚类问题时，随着样本数n的增加，不得不减少循环次数p，否则其计算量仍然是单台计算机无法胜任的。不过，该算法的特点决定了可以考虑用多核并行的方式求解规模稍大一点的聚类问题。

［1］张雁翔，祁育仙.改进遗传算法求解TSP［J］.山西电子技术（应用实践），2016（1）：28-30.

［2］马艳英.基于遗传算法的Web文档聚类算法［J］.现代电子技术，2016（1）：148-152.

［3］左倪娜.基于改进遗传算法的K-means聚类方法［J］.软件导刊，2016（4）：32-34.

［4］李芳，赵天洋.遗传算法理论及其应用进展探析［J］.技术与市场，2016（1）：87.

Application of K binary genetic algorithm in solving clustering problem

Han Hai
（Mathematics and Computer Science of Jianghan University， Wuhan 430056， China）

In this paper， a scheme of using K string string as the chromosome of genetic algorithm was put forward， and the general steps of using this algorithm were given to solve clustering problem， the applicability of the method was analyzed.

clustering； genetic algorithm； K string； chromosome

韩海（1968— ），男，江苏南京，硕士，副教授；研究方向：图形图像与模式识别。