不受线路参数变化影响的故障测距原理研究

李　澄，鲍有理，黄　瑜，施亚萍，袁磊平

（国网无锡供电公司，江苏无锡214061）

不受线路参数变化影响的故障测距原理研究

李澄，鲍有理，黄瑜，施亚萍，袁磊平

（国网无锡供电公司，江苏无锡214061）

为解决由线路参数变化引起的故障测距不准确问题，提出了不受线路参数变化影响的故障测距新原理。该原理采用集中参数线路模型，由传统的故障点等电压原理推导出线路单位长度阻抗的表达式，通过序分量法从原理上消去单位长度阻抗得到测距方程，从而实现参数未知的故障距离求解。仿真计算结果表明，提出的新原理可靠有效，无需迭代搜索求解，测距精度优良，具有良好的实际应用价值。

输电线路；参数变化；集中参数；故障定位

输电线路发生故障后，快速准确地找到故障点有利于运维人员及时恢复供电。精确的故障距离测量技术一直是研究热点。其中，行波法凭其高精度的优势已经受到广泛应用，当前对于行波法研究仅集中于信号提取的可靠性方面，信号无法可靠提取时采用行波法测距会失效，产生较大误差。智能法主要在原理上进行创新，缺乏必要的实践性，工程实际中尚未应用。从信息来源上故障测距分为单端法和双端法［1］，双端法故障测距能够在原理上克服过渡电阻和系统运行方式变化的影响，较单端测距有着明显的优势。在目前同步相量测量单元（PMU）广泛应用过程中，双端数据可同时采集，用于系统在线监视及故障分析等。

在故障测距原理的计算中，通常将线路参数作为已知量处理［2，3］。然而，实际运行过程中输电线路的参数并非固定不变，而是会受环境变化、动态过程、扰动、运行方式以及故障的影响而变化，给测距结果带来较大的误差。对于参数变化影响测距的问题，在分布参数线路模型上，文献［4］将故障距离、线路参数和非同步角作为未知量，构造非线性方程，采用牛顿拉弗逊法迭代求解实现测距，文献［5］在原理上考虑了各种因素，将故障前的电压电流数据量进行迭代求解得到修正后的线路参数，仅对非线性方程求解作了改善。文献［6］提出了动态条件下基于在线参数估计法，将估计结果作为参数修正值，数据准确性更加完善，但是同样为非线性方程迭代求解法。文献［7］对同杆双回线提出了参数识别的测距方法，在构造非线性方程的同时减少了特性阻抗未知量，仍然采用牛顿拉弗逊法迭代求解。文献［8］对同杆四回线构造了参数自适应的测距观测方程，采用最小二乘法求解。对于集中参数模型，文献［9］将故障距离、线路参数和非同步角作为未知量，构造了非线性方程，采用信赖域迭代方法求解；文献［10］采用线性系统叠加原理提出参数辨识的测距原理，将故障状态网络和故障分量网络联立，差分代替一阶和二阶微分构造求解实现测距。这些方法都需要迭代搜索求解非线性方程，初值和收敛性问题不可避免，并未从原理上解决参数未知的影响。文献［11，12］则提出了构造测距方程计算时能够消去线路参数的双端测距方法，在原理上克服了参数变化对测距的影响。

文中基于短距离线路集中参数阻抗模型提出了不受线路参数变化影响的新原理。该原理在计算过程中通过序分量法消去线路参数，克服了线路参数变化的影响。仿真结果表明提出的方法可靠有效，无需迭代求解，测距精度高，不易受过渡电阻影响。

1　测距原理

1.1线路的集中参数模型

目前，输电线路主要采用架空线或者电缆，在线路电压等级不高时，短距离架空线（长度为100 km以内）和电缆线可不计电导B0和电纳G0，通常采用如图1所示的一字型阻抗等值电路来表示。

图1　线路等值电路

在一字型阻抗等值电路中，当已知线路始端P处的电压UP、电流IP时，假设任意点D处距离始端P处的长度为d，线路单位长度阻抗为Z0，线路上任意点D处的电压UD、电流ID可以用始端的电气量来表示：

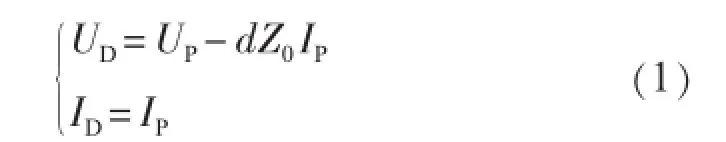
1.2测距方程推导及求解

采用单线模型表示输电线路，线路上一点发生故障，如图2所示。以P，Q为始末端的线路全长为L，故障点f距离始端P的长度为d，则故障点f距离末端Q的长度为L-d，线路始端P处的电压UP、电流IP，线路末端Q处的电压UQ、电流IQ。

图2　故障等值图

参照一字型阻抗等值电路，由基本电路定律，从P端推导至故障点f处的电压UfP及从Q端推导至故障点f处的电压UfQ可以分别表示为：

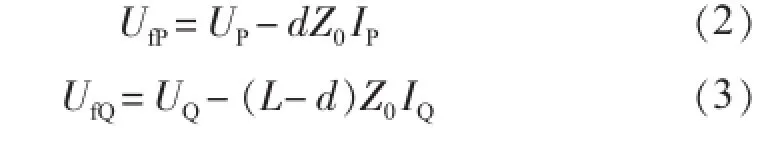
依据传统双端法故障测距原理，在故障点f处满足：

联立式（2）、（3）、（4），经整理，得线路单位长度阻抗Z0的表达式为：

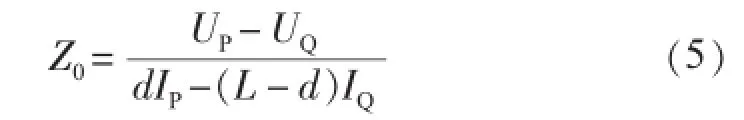
图3为线路故障时的正序、负序等值网。对于正序网络，参照单位长度阻抗计算表达式，有正序单位长度阻抗Z1：

其中：UP1为始端P的正序电压；IP1为始端P的正序电流；UQ1为末端Q的正序电压；IQ1为末端Q的正序电流。

图3　故障线路等值序网图

对于负序网络，同理，有负序单位长度阻抗Z2：

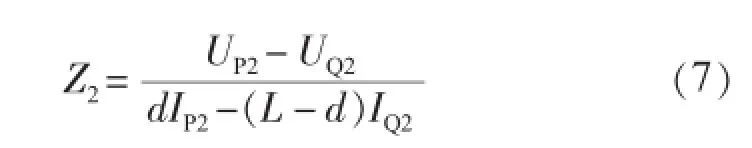
其中：UP2为始端P的负序电压；IP2为始端P的负序电流；UQ2为末端Q的负序电压；IQ2为末端Q的负序电流。

通常在输电线路中，正序单位长度阻抗Z1和负序单位长度阻抗Z2认为是相等的，即：

记故障距离百分比为d/L，联立式（6）、（7）、（8），整理得：

从式（9）中可以看出，d/L的表达式与线路基本参数无关。

2　算法实现

从故障距离百分比的表达式（9）中可以看出，测距结果仅与始末端电压、电流的正序分量和负序分量有关，而与线路单位长度阻抗无关。在实际线路运行中，发生故障前后的电压电流数据均可以从线路两端所连变电站内故障录波器上获得。计算过程中无需采用线路基本参数，从原理上消除了因线路参数变化产生的测距误差影响。此外，故障距离的值唯一且不存在伪根问题。

线路上发生故障时，由于线路全长L已知，实际故障距离为dT，依据文中提出的测距原理求得的故障距离为dC，测距误差Δ为：

其不受参数变化影响的故障测距原理的程序流程如图4所示，其测距主要步骤为：

步骤一：开始；

步骤二：输入始末端电压UP，UQ，始末端电流IP，IQ；

步骤三：计算始末端电压电流的正、负序分量UP1，UQ1，IP1，IQ1，UP2，UQ2，IP2，IQ2；

步骤四：按式（9）计算故障距离百分比dC，按照式（10）计算测距误差Δ；

步骤五：输出dC和Δ；

步骤六：结束。

3　仿真验证

参照图5所示双端测距系统模型，利用电力系统仿真软件（PSCAD）搭建一条80 km的110 kV架空输电线路进行仿真分析，双端系统参数如表1所示。

其中，线路正序阻抗Z1=0.053+j0.37Ω/km；零序阻抗Z0=0.202+j1.12Ω/km。PSCAD故障仿真的采样频率为2 kHz，故障发生时刻为0.2 s，故障延时0.05 s，双端系统中性点接地。利用矩阵实验室（MATLAB）编程计算实现测距，对故障发生后45ms之内的数据采用精度较高的差分傅氏滤波算法进行滤波，参照文中提出的原理，求得故障距离dC和误差Δ。

在过渡电阻为100Ω的条件下，设置在线路上距离始端20 km，50 km，70 km处分别发生单相接地（AG）、两相短路（AB）以及两相接地短路（ABG）故障，测距结果如表2所示。可以看出，在线路上不同位置发生不对称短路故障时的测距误差在0.1%以内，测距精度可满足现场实际要求。

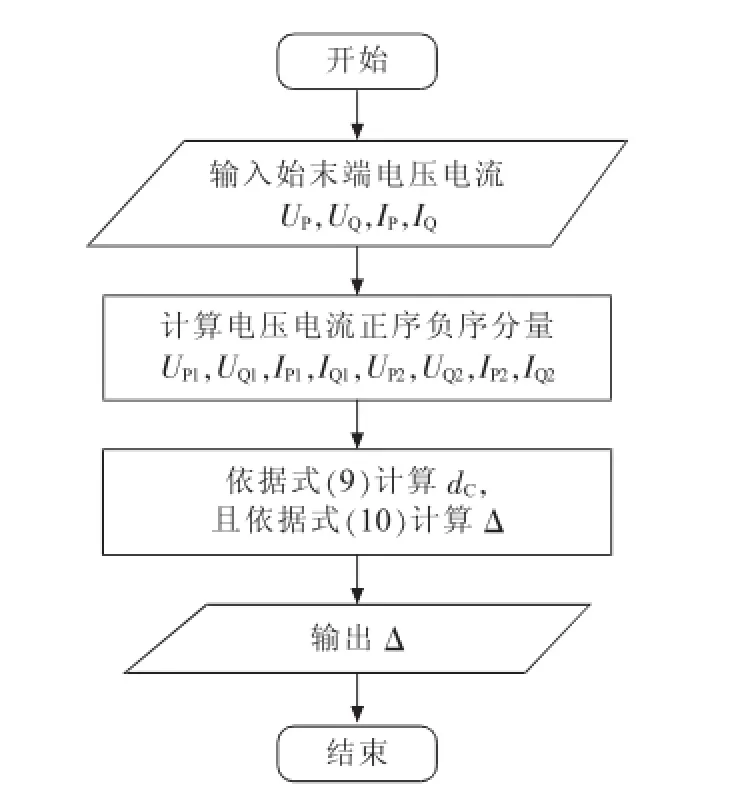
图4　程序流程

图5　双端测距系统模型

表1　双端系统参数

表2　不同位置的测距结果

在过渡电阻为100Ω情况下，线路上20 km、50 km，70 km处发生单相接地故障时，表3示出了采用文中提出的参数未知法与传统参数已知法的测距结果比较。可以看出，当线路参数（主要为正序阻抗和零序阻抗）变化时，采用参数已知方法得出的测距结果有较明显的变化，而提出的参数未知测距结果基本无变化，且较为精确。因此，新原理基本能克服参数变化影响对测距的影响。

表3　线路参数变化时的单相接地测距结果比较

从表4中可以看出，线路发生两相接地短路故障，当过渡电阻发生变化时，按照文中方法计算的测距误差范围为［0.00%，0.15%］。由此可以看出，新原理的测距结果精度良好，基本上不受过渡电阻变化的影响。

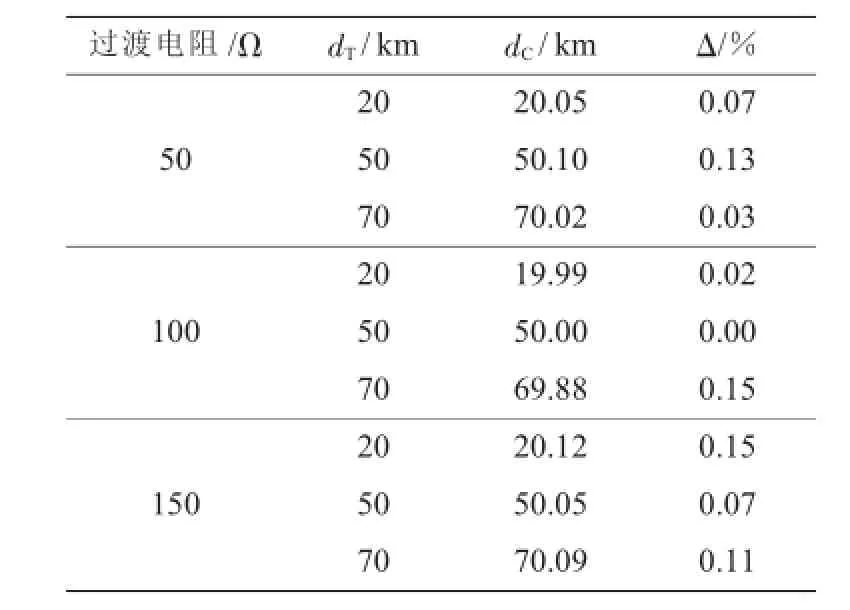
表4　过渡电阻对两相接地测距结果影响

4　结束语

文中提出的不受线路参数变化影响的故障测距原理，解决了由参数不确定性引起测距结果误差的问题。该原理在线路集中参数模型上通过双端数据构造测距方程，在计算过程中消去线路参数，从原理上使故障距离的求解与线路参数无关，且不需要迭代求解，克服了迭代法易受初值和收敛性的影响。仿真结果表明该方法可靠有效，测距精度高，不易受过渡电阻的影响，与参数已知的测距原理相比较，具有有明显的优势和良好的实际应用价值。

［1］葛耀中.新型继电保护和故障测距的原理与技术（第二版）［M］.西安：西安交通大学出版社，2007：257-258.

［2］王涛，李澄.一种混合输电线路故障测距新方法［J］.江苏电机工程，2015，34（5）：17-20，24.

［3］李澄，王锴.双端测量不同步的非对称故障测距新方法［J］.电测与仪表，2014，51（13）：55-59.

［4］车仁飞，梁军，孟昭勇.一种考虑线路参数变化的输电线路双端测距算法［J］.中国电力，2004，37（2）：45-49.

［5］梁华为，刘万顺，刘平，等.一种考虑对各种误差综合修正的线路双端测距算法［J］.继电器，2005，33（17）：7-10.

［6］刘玉萍，林圣，何文，等.动态条件下基于在线参数估计的故障定位算法［J］.电力系统自动化，2013，37（13）：103-108.

［7］赵永娴，曹小拐，刘万顺.同杆并架双回线准确参数未知时的故障测距新算法［J］.电力系统自动化，2005，29（4）：72-76.

［8］徐鹏，梁远升，王钢.同杆四回线参数自适应双端故障测距频域算法［J］.电力系统自动化，2010，34（9）：59-64.

［9］李勋，石帅军，龚庆武.采用信赖域法和双端非同步数据的故障测距算法［J］.高电压技术，2010，36（2）：396-400.

［10］索南加乐，齐军，陈福锋，等.基于R-L模型参数辨识的输电线路准确故障测距算法［J］.中国电机工程学报，2004，24（12）：119-125.

［11］APOSTOLOPOULOSCA，KORRESGN.ANovelA lgorithm for Locating Faults on Transposed/Untransposed Transm ission LinesW ithout Utilizing Line Parameters［J］.IEEE Transactions on Power Delivery，2010，25（4）：2328-2338.

［12］VIEIRA DOUGLAS A G，OLIVEIRA DIOGO B，LISBOA ADRIANO C.A Closed-form Solution for Transm ission-line Fault Location W ithout the Need of Term inal Synchronization or Line Parame ters［J］.IEEE Transactions On Power Delivery，2013，28（2）：1238-1239.

Research on Fault Location Unaffected by Parameters for Transm ission Lines

LICheng，BAO Youli，HUANG Yu，SHIYaping，YUAN Leiping
（StateGridWuxiPowerSupply Company，Wuxi214061，China）

The paper proposed anew fault location unaffected by transmission line parameters（TLPs）to eliminate the errors of the existing one caused by TLP variations.To get the new fault location，firstly the unit impedance expression is derived based on the lumped parameter circuitmodel and the basic principle that at faulty point voltages calculated from both term inals can be equal.Then an easy location equation is got by eliminating the unit impedance based on the sequence componentmethod，so that the faultpointcan be also located when the valuesof TLPsareunknown.Simulation resultsshow that thenew fault location where the faulty point is solved without iteration and search is reliable，effective，and precise，and hasagood practicalvalue.

transm ission line；parameters variation；lumped parameter；fault location

TM 77

A

1009-0665（2016）05-0067-04

李澄（1987），男，江苏江阴人，助理工程师，从事地区电网调控运行工作；

鲍有理（1966），男，安徽安庆人，研究员级高级工程师，从事电力系统继电保护技术管理工作；

黄瑜（1982），男，江苏无锡人，工程师，从事地区电网调控运行工作；

施亚萍（1972），女，江苏无锡人，技师，从事地区电网调控运行工作；

袁磊平（1974），女，江苏无锡人，技师，从事地区电网调控运行工作。

2016-04-11；

2016-06-08